ファイバー束
ファイバー束(ファイバーそく、英: fiber bundle, fibre bundle)とは、位相空間に定義される構造の一つで、局所的に 2 種類の位相空間の直積として表現できる構造の事である。
概要[編集]
単位円 S1 と線分 I = [0, 1] の直積 S1 × I は円柱の側面になる。円柱の側面と似たような図形にメビウスの輪がある。局所的には S1 の一部と線分 I = [0, 1] の直積に見えるが、全体的には円柱と異なる図形になっている。このような局所的に直積として書けるという性質(局所自明性)を持った図形を扱うのがファイバー束の概念である。
この場合の S1 を底空間といい、線分 I をファイバー(繊維)という。ファイバーを底空間に沿って束ねたとき、上の例の円柱のように全体としても直積になっていれば、その全体を自明束(じめいそく)という。自明束は基本的なファイバー束ではあるが、むしろ、メビウスの輪のように自明でないファイバー束の構造がどのようになっているのかといったことが重要である。
ファイバーはただ束ねられるだけではなく、構造群と呼ばれる位相変換群に従って張り合わされる。底空間の開被覆 {Ua}a∈A があり、その 2つの元の共通部分 Ua ∩ Ub が空でないとき、その共通部分に立っているファイバーはどのように貼り合わされるべきか? という事、すなわち、直積 Ua × F と Ub × F の重なり方を記述するのが構造群である。
ファイバー束の概念は、ホイットニーに始まる。ホイットニーは多様体上のベクトル場から接ベクトル空間をファイバーに持つ接ベクトル束を構成し、その一般化としてファイバー束に到達した。その後、陳省身(Shiing-Shen Chern) による研究は、ファイバー束と接続を関連させ微分幾何学を大域的理論へと導いていくことになり、ゲージ理論などの基礎も成している。また、微分幾何学に留まらず、様々な幾何学の基本的な道具となり、その適用範囲は広い。さらにファイバー束はセールやヒューレッツらによってファイバー空間として一般化され、代数的位相幾何学を支える概念の一つにもなった。
定義[編集]
束[編集]

- π: E → B
があるとき、E を全空間 (total space)、B を底空間 (base space)、π を射影 (projection)、これらの組 (E, π, B) を束 (bundle, バンドル) という[要出典]。
- (E, B, π) のような順序で書かれる場合もある。
x ∈ B に対し、Fx = π−1(x) を x 上のファイバー (fibre, fiber) という。
以下で扱う座標束やファイバー束の場合、任意の x ∈ B に対し Fx は x によらず位相空間 F と同相になる。すなわち、x, y ∈ B に対して、Fx と Fy は同相である。しかし、一般の束では、そのような関係は無い。例えば楕円曲面などでは、ほとんどのファイバー(非特異ファイバー)とは異なる特異ファイバーと呼ばれるファイバーがある。
座標束[編集]

ここでは、座標束 {E, π, B, F, G, Ua, φa}a∈A を定義する。添字集合などを省略して (E, π, B, F, G, Ua, φa) などとも書く。
束 (E, π, B) と位相空間 F, F の効果的な位相変換群 G, 底空間 B の開被覆 {Ua}a∈A が与えられているとする。Ua を、座標近傍 (coordinate neighborhood) という。各座標近傍 Ua には同相写像
- φa: Ua × F → π−1(Ua)
が存在し、任意の x ∈ Ua および f ∈ F に対して
- π ∘ φa(x, f) = x
を満たす。
- この φa という同相写像によって Ua × F と π−1(Ua) はしばしば同一視される。座標束を説明する図を描くときも Ua × F という直積の図を π−1(Ua) とみなして説明することも少なくない。φa−1 を局所自明化という。
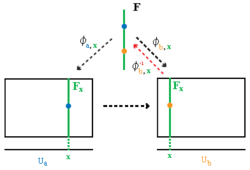
a を固定した F 上の
- φa, x: F → π−1(Ua)
- φa, x(f) = φa(x, f)
という写像は、x ∈ Ua ∩ Ub に対して、
- gba(x): F → F
- gba(x)(f) := φ −1
b, x ∘ φa, x(f)
を導く。
ここで、gba(x) ∈ G であり、
- gba: Ua ∩ Ub → G
は連続写像であるとし、G は位相変換群としてできるだけ要素の少ない小さいものをとるとする。
このような性質を持つ (E, π, B, G, {Ua, φa}a∈A) という組を座標束 (coordinate bundle) といい、F をファイバー、G を構造群 (structure group)、E を全空間、π を射影、B を底空間、φa を、座標関数 (coordinate function)、gba を座標変換 (coordinate transformation) という。
- 一般の束と違って、ファイバーは点に依らない位相空間である。正確には、任意の x ∈ B に対し x 上のファイバー Fx が、ファイバー F と同相となっている。そして各点での座標変換が、構造群という代数的な構造によって決まっているという点も重要である。
ファイバー束[編集]
- 座標束をここで述べるような同値関係で分類するとファイバー束が得られる。多様体において座標近傍系を極大座標近傍系にし、座標の取り方によらない幾何学を目指したのと同様に、座標束を座標近傍 {Ua} や座標関数 {φa} のとり方によらないように分類したものがファイバー束である。つまりファイバー束を具体的に調べる際に、特定の開被覆を取って調べたりする場合、そこで調べているものは座標束ということになる。
座標近傍や座標関数の取り方の違う 2つの座標束 (E, π, B, F, G, Ua, φa) および (E, π, B, F, G, Vb, ψb) があるとき、x ∈ Ua ∩ Vb に対して
- hba(x) := ψ −1
b, x ∘ φa, x
が、hba(x) ∈ G となり
- hba: Ua ∩ Vb → G
が連続写像であるとき、この 2つの座標束は同値 (equivalent) であるといい、この同値関係による同値類をファイバー束あるいは G 束 (G-bundle) といい、ξ = (E, π, B, F, G) と書く。F や G なども省略して、π: E → B によってファイバー束を表すこともある。

ファイバーと構造群の等しい 2つのファイバー束
- ξ1 = (E1, π1, B1, F, G)
- ξ2 = (E2, π2, B2, F, G)
に対し、連続写像
- ηE: E1 → E2
- ηB: B1 → B2
があり、
- π2 ∘ ηE = ηB ∘ π1
を満たすとする。x ∈ B1 に対し
- y = ηB(x)
と書くことにすると、ηE は、x 上のファイバー Fx を y 上 のファイバー Fy に写す。すなわち、この (ηE, ηB) という写像は、ファイバーという構造を保存する写像である。さらに ηE が同相写像であるとき (ηE, ηB) を束写像 (bundle map) という。
- ηB は ηE から条件を満たすように定まる写像と定義して、ηE の事を束写像と呼ぶこともある。さらに底空間も等しい 2つのファイバー束
- ξ1 = (E1, π1, B, F, G)
- ξ2 = (E2, π2, B, F, G)
で ηB が恒等写像となる束写像 (ηE, ηB) が存在するとき、この 2つのファイバー束は同値であるといい、ξ1 ≡ ξ2 と書く。
切断[編集]

ファイバー束 ξ = (E, π, B, F, G) に対して、連続写像
- s: B → E
が、任意の x ∈ B に対し
- π ∘ s(x) = x
を満たすとき、s を ξ の切断 (section, cross-section) あるいは、断面という。切断は必ずしも存在しない。
- 底空間上の点 x に対し s(x) が定まる。例えば多様体上のベクトル場であれば、多様体上の点 x に対しベクトル s(x) が対応する。逆に言えば、ベクトル場の集合がどういう空間に入っているべきかを考えたものがファイバー束(この例では多様体を底空間に持つベクトル束)である。
具体的な計算として座標束を考える時などには、座標近傍 Ua 上での切断が必要になる場合がある。同様に
- sa : Ua → E
が、任意の x ∈ Ua に対し
- π ∘ sa(x) = x
を満たすとき、sa を Ua 上の局所切断 (locally section, locally cross-section) あるいは、局所断面という。これに対し上記の s を大域切断などという。
例[編集]
自明束[編集]
全空間を E = B × F とし、π: E → B を第一成分への射影とする。すなわち、x ∈ B, f ∈ F に対して、π(x, f) = x とする。このとき E は F の B 上のファイバー束である。ここで E は、局所的にだけでなく大域的に、底空間とファイバーの直積となっている。そのようなファイバー束を自明束 (trivial bundle) という。S1 × [0, 1] や S1 × R1 のような円柱や、自然数 m, n > 0 に対して Rm+n = Rm × Rn などのように直積で表される図形は、自明束としての構造を持つ。可縮なCW複体上の任意のファイバー束は自明である。
メビウスの帯[編集]

おそらく最も単純な非自明な束 E の例はメビウスの帯であろう。メビウスの帯は底空間 B として帯の中心に沿って一周する円を持ち、ファイバー F として線分を持つ。そのため、メビウスの帯は線分の円上の束である。点 x ∈ B の近傍 U は弧である。図では、これは正方形の一辺である。原像 π−1(U) は図では4つ並んだ(少し捩れた)正方形である。同相写像 φ は U の原像を円柱の断片へと写す。それは曲がってはいるが、捩れてはいない。
対応する自明束 B × F は円柱(の側面)ということになるが、メビウスの帯は全体として「捩れている」。この捩れは大域的にしか観察できないことに注意しよう。局所的には、メビウスの帯と円柱は同一である(1度垂直に切ればどちらも同じ空間になる)。
構造群 G は、ファイバーを反転させる変換 a を用いて G = {1,a}となる。これは Z2 と同型である。
クラインの瓶[編集]
メビウスの帯と似た非自明な束はクラインの瓶である。これは「捩れた」円の別の円上の束と見ることができる。対応する捩れていない(自明な)束は2次元トーラスS1 × S1 である。
 |
 |
被覆写像[編集]
被覆空間 (covering space) は束射影が局所同相であるようなファイバー束である。ファイバーは離散空間であることが従う。
ベクトル束と主束[編集]
ベクトル束と呼ばれる、ファイバー束の特別なクラスがあり、これはファイバーがベクトル空間であるようなファイバー束である。(ベクトル束であるためには、束の構造群は線型群でなければならない)。ベクトル束の重要な例には、滑らかな多様体の接束や余接束がある。任意のベクトル束から、主束(下記参照)である、基底の枠束を構成することができる。
主束と呼ばれる、ファイバー束の別の特別なクラスがあり、これはその上に群 G による自由かつ推移的な作用が与えられていて、各ファイバーが主等質空間であるような束である。束はしばしば主 G 束と呼ぶことによって群とともに特定される。群 G はまた束の構造群でもある。G のベクトル空間 V 上の表現 ρ が与えられると、構造群として ρ(G)⊆Aut(V) なるベクトル束を構成でき、これを同伴束と呼ぶ。
関連項目[編集]
参考文献[編集]
- Steenrod, Norman (1951), The Topology of Fibre Bundles, Princeton University Press, ISBN 0-691-08055-0
- Bleecker, David (1981), Gauge Theory and Variational Principles, Reading, Mass: Addison-Wesley publishing, ISBN 0-201-10096-7
- Ehresmann, C. "Les connexions infinitésimales dans un espace fibré différentiable". Colloque de Topologie (Espaces fibrés), Bruxelles, 1950. Georges Thone, Liège; Masson et Cie., Paris, 1951. pp. 29–55.
- Husemöller, Dale (1994), Fibre Bundles, Springer Verlag, ISBN 0-387-94087-1
- Michor, Peter W. (2008), Topics in Differential Geometry, Graduate Studies in Mathematics, Vol. 93, Providence: American Mathematical Society (to appear).
- Voitsekhovskii, M.I. (2001), “Fibre space”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
外部リンク[編集]
- Fiber Bundle, PlanetMath
- Rowland, Todd. "Fiber Bundle". mathworld.wolfram.com (英語).
- Making John Robinson's Symbolic Sculpture `Eternity'
- Sardanashvily, G., Fibre bundles, jet manifolds and Lagrangian theory. Lectures for theoreticians,arXiv: 0908.1886
