ISO 216
| Cシリーズ | |
|---|---|
| C0 | 917 × 1297 |
| C1 | 648 × 917 |
| C2 | 458 × 648 |
| C3 | 324 × 458 |
| C4 | 229 × 324 |
| C5 | 162 × 229 |
| C6 | 114 × 162 |
| C7/6 | 81 × 162 |
| C7 | 81 × 114 |
| C8 | 57 × 81 |
| C9 | 40 × 57 |
| C10 | 28 × 40 |
| DL | 110 × 220 |
| Bシリーズ | |
|---|---|
| B0 | 1000 × 1414 |
| B1 | 707 × 1000 |
| B2 | 500 × 707 |
| B3 | 353 × 500 |
| B4 | 250 × 353 |
| B5 | 176 × 250 |
| B6 | 125 × 176 |
| B7 | 88 × 125 |
| B8 | 62 × 88 |
| B9 | 44 × 62 |
| B10 | 31 × 44 |
| Aシリーズ | |
|---|---|
| A0 | 841 × 1189 |
| A1 | 594 × 841 |
| A2 | 420 × 594 |
| A3 | 297 × 420 |
| A4 | 210 × 297 |
| A5 | 148 × 210 |
| A6 | 105 × 148 |
| A7 | 74 × 105 |
| A8 | 52 × 74 |
| A9 | 37 × 52 |
| A10 | 26 × 37 |
ISO 216は、今日世界の多くの国で使われている、紙の寸法を規定する国際規格である。A4シリーズの紙のサイズを定めている。
- ISO 216(1975年)は、AシリーズとBシリーズの紙を定義している。
- ISO 269(1985年)は、封筒用のCシリーズの紙を定義している。
- ISO 217(1985年)は、RAシリーズとSRAシリーズの未仕上げ紙を定義している。
この国際規格は、ドイツで1922年に定められたドイツ工業規格(DIN 476)に基づいている。この規格に含まれる形式のいくつかはフランス革命中にフランスで独自に発明されたが、後に失われた[1]。この規格で使われているアスペクト比は、1786年10月25日に書かれたゲオルク・クリストフ・リヒテンベルクの詩で引用されている[2]。
アスペクト比[編集]
アスペクト比が2の平方根の長方形は、長い辺に垂直に半分に切るとアスペクト比が逆数になる(つまり、長辺の向きをそろえるとアスペクト比が同じになる)という幾何学的性質がある。長方形の長い辺をx、短い辺をyとすると、次の方程式は、長方形のアスペクト比が、半分の大きさの長方形とどのような比例関係になっているかを示す
- を計算すると となり、アスペクト比はとなる。
ちなみに、は白銀比である。
各系列[編集]
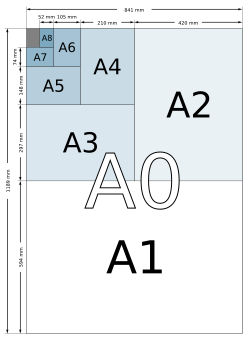
Aシリーズ[編集]

Aシリーズの紙は、のアスペクト比を持つ。この比率は古くから美しい比とされ白銀比と呼ばれる。ただし端数はミリメートル単位に丸められる。A0は1m2の面積を持ち、続くサイズ(A1,A2,A3・・・)は、前のサイズの紙を短い辺に平行に切ったもの(即ち、A(n+1)の長い辺は、Anの短い辺と同じ長さ)である。
このシリーズで最も頻繁に使われるのはA4 (210 × 297 mm)である。A4は、北アメリカでよく用いられる国際判 (216 × 279 mm)と比べ、6mm狭く、18mm長い(画像)。
Aの紙の正確な縦の長さ(mm)は、という式で表せる。記号 は床関数(切捨て)である。
Bシリーズ[編集]

Bシリーズは、同じ番号のAシリーズの大きさと1つ小さいAシリーズの大きさの幾何平均となっている。例えば、B1はA1とA0の幾何平均である。B0の2辺の長さは、1mとmである。日本工業規格(JIS)で定められた、国際規格とは別のBシリーズもある。JISのBシリーズの長さは、Aシリーズの約1.22倍である。
Bの紙の正確な縦の長さ(mm)は、という式で表せる。記号 は床関数である。
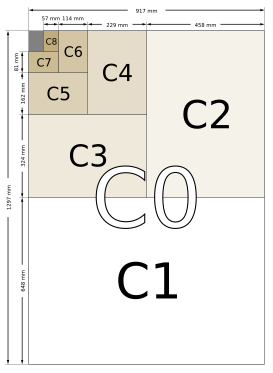
Cシリーズ[編集]

Cシリーズは、同じ番号のBシリーズの大きさとAシリーズの大きさの幾何平均となっている。例えば、C2はB2とA2の幾何平均である。Cシリーズは主に封筒に使われる。A4の用紙はC4の封筒にぴったり収まる。Cシリーズの封筒は、Aシリーズの大きさと比例関係にある。例えば、A4の紙を半分に折ってA5にすると、C5の封筒にぴったりと収まる(C5はC4の封筒を半分に折ったものと同じサイズである)。
Cの紙の正確な縦の長さ(mm)は、という式で表せる。記号 は床関数である。
許容誤差[編集]
この規格で定められた許容誤差は次の通りである。
- 150mm以下の大きさでは、±1.5 mm。
- 150mmから600mmの大きさでは、±2.0 mm。
- 600mm以上の大きさでは、±3.0 mm。
A,B,Cの比較[編集]
出典[編集]
- ^ “Loi sur le timbre (No. 2136)”. 2009年2月11日閲覧。
- ^ “Lichtenberg’s letter to Johann Beckmann”. 2009年2月11日閲覧。
外部リンク[編集]
- International standard paper sizes: ISO 216 details and rationale
- ISO 216 at iso.org