近藤効果

近藤効果(こんどうこうか、Kondo effect)とは、磁性を持った極微量な不純物(普通磁性のある鉄原子など)がある金属では、温度を下げていくとある温度以下で電気抵抗が上昇に転じる現象である。これは通常の金属の、温度を下げていくとその電気抵抗も減少していくという一般的な性質とは異なっている。現象そのものは電気抵抗極小現象とよばれ、1930年頃から知られていたが、その物理的機構は1964年(昭和39年)に日本の近藤淳が初めて理論的に解明した[1]。近藤はこの業績によって1973年(昭和48年)に日本学士院恩賜賞を受章した。
現象[編集]
金属は電圧を加えると、金属内の伝導電子が加速され電流が流れる。これを電気伝導という。
一方で、この伝導電子には電気抵抗がはたらく。金属の電気抵抗の主な要因は、金属内に含まれる不純物などによる格子欠陥と、原子の熱振動の2つである。不純物による抵抗は温度に依存せず一定である。熱振動による抵抗は、温度を下げると小さくなり、低温では抵抗は温度Tの5乗に比例する。そのため、金属の電気抵抗は通常、温度を下げると減少し、絶対零度で、一定値(=不純物による抵抗値)に落ち着く。
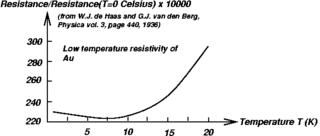
しかし、金属によっては、ある温度までは温度が下がると電気抵抗も減少するが、さらに温度を下げると電気抵抗は逆に増大するという、通常では起こりえないふるまいを見せる。この現象は、1933年、ド・ハース、ド・ブール、ファン・デン・バーグが、金の電気抵抗を測定したときに初めて観測された[2]。
その後の研究により、この現象は金(Au)、銀(Ag)、銅(Cu)などに鉄(Fe)、マンガン(Mn)、クロム(Cr)などの磁性不純物を微量に加えた金属で起こることが明らかになった。
理論[編集]

低温における電気伝導度の増加の原因については長年未解決であったが、後に、近藤効果(磁性不純物の磁気モーメントと伝導電子の磁気モーメントの交換相互作用〈s-d交換相互作用〉)によるものであることが明らかになった。
磁性不純物の一番外側の電子殻である3d電子殻は、スピン角運動量を持っている。このスピンと、伝導電子(s)が相互作用するのがs-d交換相互作用である。近藤は、アンダーソン模型とボルン=オッペンハイマー近似を用いて摂動の2次の効果まで考慮し、この作用が温度Tの対数(lnT)に比例することを導いた。交換相互作用の係数が負のとき、この値は温度が減少するにつれて増大することになる。この項と、熱振動の項を合わせることで、電気抵抗が極小になることが説明できたのである。
近藤の理論では電気抵抗は絶対零度で無限大に発散する。しかし実際には、電気抵抗は絶対零度に近づくにつれ正常な振る舞いとなり、有限値へと収束する。これは低温においては、磁性不純物の磁気モーメントと伝導電子の磁気モーメントが反強磁性的に結合した一重項基底状態 (Kondo singlet) として磁性不純物の磁気モーメントが見かけ上消滅するためであり、このことは芳田奎によって示された。
この近藤による磁気モーメントの交換相互作用による異常な振る舞いから、磁性不純物の磁気モーメントが基底状態となった正常な振る舞いへと移り変わる温度を近藤温度とよぶ。よってはほぼ磁性不純物の磁気モーメントと自由電子の磁気モーメントの結合エネルギーに相当する(はボルツマン定数)。ウィルソンの理論によれば、近藤温度は比熱が極大となるときの温度の3倍となる。また、近藤温度を基準としたを考えると、様々な物質で電気抵抗率、磁化率、比熱が同じ温度依存性を示す(スケーリング則)。近藤温度は数 mK 程度のものもある一方、中には1000 K程度のものもあるなど、それぞれの合金によって大きく異なる。
以上のことを数式を用いて述べると以下のようになる。
まず、近藤の論文によれば、近藤効果を含めた電気抵抗の温度依存性は
とかける。ここでは不純物濃度であり、は残留抵抗、は格子振動の寄与を表す。近藤は右辺第三番目の対数依存の項を導いた。伝導電子の磁気モーメントと不純物の磁気モーメントの交換相互作用が強磁性的である場合、近藤の項の符号は正となり、近藤効果は発生しない。フェルミ液体ではフェルミ液体の性質による抵抗への寄与が加わる。
抵抗が最小となる温度は
により求めることができ、
が電気抵抗極小の温度である。この温度は不純物濃度の乗に比例している。
アブリコソフは1965年に摂動による高次の寄与も考慮に入れ、近藤効果による抵抗Rを
と計算した(Jは交換相互作用の強さを表す定数、Dは伝導電子のバンド幅の半分、はフェルミエネルギーの状態密度)。この式によれば、電気抵抗は近藤温度で発散することとなる[3]。
また磁化率は
と書け、電気抵抗と同じくで発散する(Cはキュリー定数)。これは芳田・興地によって示された[4][5]。また、比熱にも同様の異常があらわれる。
近藤効果が起きるためには、金属中の磁性原子は相互作用を起こさない程度に希薄でなければならない。このような合金を希薄磁性合金、または近藤合金とよぶ。
理論の拡張と応用[編集]
近藤の理論は絶対零度では物理量にlog発散をともなう。また近藤は摂動の2次の効果を計算し、の項を導いたが、さらに高次の摂動計算を行うと、を含む項があらわれ、低温ではこれらの項も無視できない。これはある温度以下では摂動論が破綻するということを意味している。この困難は後にフィリップ・アンダーソンのpoor man's scaling (1970年)[6] や、ケネス・ウィルソンの繰り込み群 (1975年)[7]によって解決され、局在スピンの状態からパウリ常磁性の状態に連続的に移り変わることが示された。ウィルソンはこの業績により1982年にノーベル物理学賞を受賞した。その後、Nozieres、山田耕作らによって局所フェルミ液体として近藤効果を捉えられることが示された。また、低温度に近づくにつれ、エネルギーギャップが生じ、フェルミ面がギャップ中に埋もれてしまうことに起因し、電気的特性の温度依存性が半導体(あるいは絶縁体)的に振舞う相領域におけるものを近藤絶縁体という。
近藤効果は物理学において漸近的自由性の最初に知られた例である。近藤効果では、漸近的自由性は磁気不純物の局在モーメントと伝導電子間の相互作用が低温/低エネルギーで摂動では取り扱えないほど強くなることにあたる。漸近的自由性のより複雑な形式としては量子色力学の理論での漸近的自由性があり、クォークにおける強い相互作用が高エネルギーでは弱く、低エネルギーでは強く働くことに相当する。これにより、クォークの閉じ込めがおきているが、近藤効果もこれに類似した現象であるといえる。なお、フランク・ウィルチェック、デイビッド・グロス、H. デビッド・ポリツァーの3人は強い相互作用の理論における漸近的自由性の発見で2004年にノーベル物理学賞を受賞している。
主に「磁性不純物」によって構成されている合金についても理論を拡張し、それらの合金でみられる重いフェルミ粒子は近藤効果が元となって生じていると考えられている。これは特にセリウム、プラセオジム、イッテルビウムのような希土類元素(レアアース)や、ウランのようなアクチノイドを基本とした金属間化合物で起きる。これらの物質では、非摂動的な相互作用が強いため、自由電子の有効質量が1000倍にも増加したようにみえる。言い換えると、自由電子は相互作用により劇的に運動速度が遅くなっている。その結果として、これらの物質の中には超伝導を起こすものがある。
更に最近では、プルトニウムの普通でない金属δ相(面心立方格子構造)を理解するためには、近藤効果の現れが必要であると考えられている。また、量子ドットにおける近藤効果も報告されている[8]。近藤の業績を引用する論文も増えつつあり、ノーベル賞の候補とされていた[9]。
脚注[編集]
- ^ Jun Kondo (3 1964). “Resistance Minimum in Dilute Magnetic Alloys”. Progress of Theoretical Physics (Kyoto, JAPAN: 京都大学基礎物理学研究所) 32 (1): 37-49. doi:10.1143/PTP.32.37. ISSN 1347-4081 (オンライン), 0033-068X (紙媒体) 2008年10月9日閲覧。.
- ^ W. J. de Haas, J. de Boer and G. J. van den Berg, Physica,1 (1933/34) 1115
- ^ 芳田(1990)p34
- ^ K.Yoshida and A.Okiji, Prog. Theor. Phys., 34 (1965) 505
- ^ 山田耕作「金属中の磁気モーメント」 『日本物理学会誌』、vol.60(2)、2005年
- ^ P. W. Anderson and G. Yuval, "Exact Results in the Kondo Problem. II. Scaling Theory, Qualitatively Correct Solution, and Some New Results on One-Dimensional Classical Statistical Models", Phys. Rev. B 1:4464-4473 (1970)
- ^ K.G. Wilson, "The renormalization group: critical phenomena and the Kondo problem", Rev. Mod. Phys. 47, 4, 773.
- ^ D. Goldhaber-Gordon et al., “Kondo effect in a single-electron transistor”, Nature 391, 156–159 (1998).
- ^ 2011年1月24日の東京新聞朝刊21面
参考文献[編集]
- The Kondo Problem to Heavy Fermions - Monograph on the Kondo effect by A.C. Hewson (ISBN 0-521-59947-4)
- Exotic Kondo Effects in Metals - Monograph on newer versions of the Kondo effect in non-magnetic contexts especially by D.L. Cox and A. Zawadowski (ISBN 0-7484-0889-4) - 多チャンネル近藤効果等
- 芳田奎『近藤効果とは何か』 丸善、1990年、ISBN 978-4621034408
- 斯波弘行 『新版 固体の電子論』 和光システム、2010年、『固体の電子論』 丸善、1996年、ISBN 978-4621041352
- 近藤淳 『金属電子論―磁性合金を中心として』 裳華房、1983年、ISBN 978-4785323172 厳密解や繰り込み群等様々なアプローチ
















![{\displaystyle \chi _{\mathrm {imp} }(T)={\frac {C}{T}}\left[1+{\frac {J\rho }{N}}\left(1-{\frac {J\rho }{N}}{\rm {ln}}{\frac {k_{B}T}{D}}\right)^{-1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e734a39a819ded443947ec912a4c1afe55b63dfb)



