ホール効果

ホール効果（ホールこうか、Hall effect）とは、電流の流れているものに対し、電流に垂直に磁場をかけると、電流と磁場の両方に直交する方向に起電力が現れる現象。主に半導体素子で応用される。1879年、米国の物理学者エドウィン・ホール(Edwin Herbert Hall, 1855-1938)によって発見されたことから、このように呼ばれる。

概要

ホール効果 青い丸は電子の流れ (電流の流れている向きとは逆).
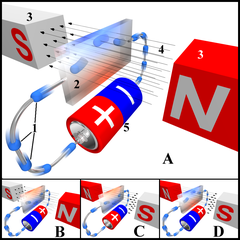
番号:
1. 電子 (電流の流れている向きとは逆！)
2. ホール素子
3. 磁石
4. 磁場
5. 電源
解説:
図ＡでN型ホール素子の場合、下部はイオン化したドナーにより正に帯電する(Ｐ型の場合は、イオン化したアクセプタにより負に帯電する)。 図Ｂ、図Ｃはそれぞれ電流の向き、または磁場の向きが図Ａとは逆になっており、帯電の極性が逆転する。 図Ｄでは電流の向きと磁場の向きの両方が図Ａとは逆であり、図Ａと同じ向きに帯電する。

p型またはn型の半導体試料において、x方向に電流を流し、ｚ方向に磁場をかける。この時試料を流れている荷電粒子（キャリア）は磁場によるローレンツ力を受けてｙ方向に加速される。これによって、試料の表面にキャリアがたまり、電流と磁場の両方に直交する方向に電場（ホール電場）が生じ、起電力が発生する。ホール効果はホール素子による磁場の検出のほか、半導体の電気的特性の測定に応用される。ホール電圧の符号と大きさから半導体のキャリアの種類と密度がわかる。また、金属は半導体に比べキャリア密度が大きく、ホール電圧が微小な値となるため、この現象を利用した物性測定は半導体が主である。

しかしながら、強磁性金属など磁化を帯びた物質中では、この磁化に起因するホール電圧が生じることもある。このような強磁性体の磁化に起因するホール効果を特に異常ホール効果と呼ぶ。また物質中のスピン軌道相互作用に起因してそれぞれ逆向きのスピンを有するキャリアが逆方向へと散乱されるスピンホール効果も近年注目を集めている。

関係式

試料に図のようにｘ方向に電流を流しながら、 これと垂直な ｚ方向に磁場を加えると、 磁場中を動くキャリアはローレンツ力を受ける。

キャリアの電荷を$q$、速度を$v$とすると ローレンツ力$\boldsymbol{\mathit{F_L}}$は

$\boldsymbol{\mathit{F_L}} = q(\boldsymbol{\mathit{v}}\times\boldsymbol{\mathit{B}})$

となる。

試料内に電流が流れている場合、キャリアは平均して一定の速度でx方向に進むようになるため,平均してｙ方向に

$\left\langle F_L \right\rangle=-q\left\langle v_x \right\rangle B_z$

という力を受け加速する。

すると、正孔が多数キャリアである場合(p型半導体)、面Bに正孔が溜まり、正に帯電する。逆に面Aは正孔不足となり負に帯電する。

また、電子が多数キャリアである場合(n型半導体)、面Bに電子が溜まり、負に帯電する。逆に面Aは電子不足となり正に帯電する。

したがって、y方向に電場$E_y$が発生する。この電場$E_y$をHall電場という。

キャリアがy方向の電場成分から受ける力$qE_y$と ローレンツ力$\left\langle F_L \right\rangle$のy成分とが打ち消し合い、平衡状態となる。

その時、Hall電場$E_y$は

$\left\langle F_L \right\rangle+qE_y=-q\left\langle v_x \right\rangle B_z+qE_y=0$…(1)

で決まる。

キャリアが一種類の場合、x方向の電流密度$j_x$は、$n$をキャリア密度とすると

$j_x=nq\left\langle v_x \right\rangle$

と書ける。

この式と(1)から　$\quad$ $q\left\langle v_x \right\rangle$ $\quad$ を消去すると

${E_y \over j_xB_z}={1 \over nq}$…(2)

となり、$\quad$ $R_H={E_y \over j_xB_z}$ $\quad$ をHall係数という。

Hall係数を測定することにより、キャリアの種類と密度が決定できる。

また、電流$I_x$は,試料の厚さを$t$、幅を$b$とすれば

$I_x=j_xbt$…(3)

である。

したがって、A面を基準にしたB面の電位（Hall電圧$V_H$）は(2)、(3)式から

$V_H=E_yb={1 \over nq}{I_xB_z \over t}=R_H{I_xB_z \over t}$

で与えられる。

一般にキャリア密度をn、キャリアの電荷をeとして

$|R_H| = \frac{\gamma_H}{ne}$

の関係がある。ここでγ_Hは散乱因子と呼ばれる。

電流方向の電場をE_jとして、

$\theta _H = E_H / E_j$

をホール角(Hall angle)と呼ぶ。

また、電気伝導度σとホール係数Rの積

$\mu_H = |R_H| \sigma = \mu \gamma_H$

をホール移動度(Hall mobility) と呼ぶ。ここでμはドリフト移動度である。

関連項目

• 量子ホール効果
• 半導体-ホール素子
• キャリア-伝導電子
• ローレンツ力
• コンデンサー
• 渦電流
• 電気素量
• Eric Fawcett
• ホールスラスタ
• ホール プローブ
• Nernst effect
• Nernst-Ettinghausen effect
• スピンホール効果
• 熱ホール効果
• トランスデューサー
• ヴァン・デル・パウ法
• 物性物理学

参考文献

• 黒沢達美 『物性論―固体を中心とした』 裳華房、2002年2月。ISBN 4785321385。