磁気単極子 、磁気モノポール (英 : magnetic monopole )とは単一の磁荷 のみを持つもののことである。
2021年現在に至るまで素粒子としては発見されていない。宇宙のインフレーション の名残として生み出されたと仮定されるものの一つであり、スーパーカミオカンデ などで磁気単極子を観測する試みが続けられている。
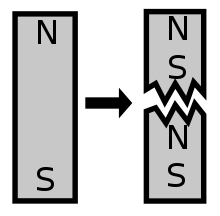
棒磁石 を切断しても、N極とS極のみを取り出すことはできない。磁石 にはN極、S極の二つの磁極 が必ず存在し、この組み合わせを磁気双極子 という。N極のみ、およびS極のみを持つ磁石、磁気単極子(モノポール)は2021年現在まで観測されていない。例えば両端がそれぞれN極とS極の棒磁石を真ん中で二つに折ったとしても、同じく両端がそれぞれN極とS極の棒磁石が二つできるだけで、N極S極のみを単純に取り出すことはできない。電磁石 を考えれば、こうなることは容易に理解できる。電磁石は電流を流したコイルであり、これを二つに分割しても、巻き数が半分になった電磁石が二つ生まれるだけである。永久磁石についても、それを構成する物質の原子が電磁石と同じ働きをしているものであり、原理としては同じである。マクスウェルの方程式 により代表される古典電磁気学はこの前提のもとに構成されている。
その一方で、電気については、プラスとマイナスの二つが存在し、これらは単独で取り出す事が可能である。これは電気の根元がプラスの陽子 とマイナスの電子 に由来しているからである。そして、古典電磁気学は電気と磁気の関係について対称であり、この関係を逆にする事が可能である。普通は、コイルを流れる電気によって磁力を発生する、言い換えれば円周上を周回する電子の運動によって磁界が生じる。これを、磁気単極子が円周上を周回する事によって電界が生じるというモデルに置き換える事ができるのである。つまり、マクスウエルの方程式は磁気単極子の存在を許すように容易に改変できる。さらに1931年にディラック は量子力学でも磁気単極子を考えることが可能であり、しかもそれが可能になるための条件から電荷及び磁荷の最小単位の存在が導かれることを示して磁気単極子が一躍注目をあびた。
2013[ 1]
予想される大統一理論 においては、クォーク とレプトン は本来同じ粒子の異なった状態であり、インフレーションの際の相転移によって分化したとされ、相互に変換可能であるとされる。陽子内のクォークがレプトンに変化するとバリオン数 を保持できなくなり陽子崩壊 が発生する。しかし陽子の予想寿命が極めて長いことからもわかるようにクォークからレプトンへの変化は極めて低い確率でしか発生しない。だがモノポールはインフレーション以前のクォークとレプトンが分化する前の空間の位相欠陥 であり、その中心部付近においてはクォークとレプトンは分化することができず、分化前の粒子に戻ってしまい、そこから通常空間に復帰した粒子はクォークにもレプトンにも変化する可能性がある。そのため陽子や中性子のクォークがモノポールの磁力で引き付けられ、中心部付近を通過してレプトンに変化すると陽子崩壊が発生する。モノポール自身は外部からのクォークを変換しただけで不変であるので、これを触媒 に見立てることができる。これらの作用を予想した人物の名を取ってルバコフ効果と呼ぶ場合もある。
スーパーカミオカンデ では大統一理論 の証明の一環としてモノポールの探索をしている。
ディラックによれば、「磁気単極子の存在」を仮定した場合、マクスウェルの方程式は次のようになる。
{
∇
⋅
B
=
ρ
m
∇
×
E
=
−
(
∂
B
∂
t
+
J
m
)
∇
⋅
D
=
ρ
e
∇
×
H
=
J
e
+
∂
D
∂
t
{\displaystyle {\begin{cases}{\begin{aligned}\nabla \cdot {\boldsymbol {B}}&=\rho _{\mathrm {m} }\\\nabla \times {\boldsymbol {E}}&=-\left({\dfrac {\partial {\boldsymbol {B}}}{\partial t}}+{\boldsymbol {J}}_{\mathrm {m} }\right)\\\nabla \cdot {\boldsymbol {D}}&=\rho _{\mathrm {e} }\\\nabla \times {\boldsymbol {H}}&={\boldsymbol {J}}_{\mathrm {e} }+{\dfrac {\partial {\boldsymbol {D}}}{\partial t}}\end{aligned}}\end{cases}}}
あるいは電磁ポテンシャル を使えば次のようになる。(簡単のためローレンツゲージ をとる)
E
=
−
∇
ϕ
e
−
∂
A
e
∂
t
−
1
ε
0
∇
×
A
m
H
=
−
∇
ϕ
m
−
∂
A
m
∂
t
+
1
μ
0
∇
×
A
e
{\displaystyle {\begin{aligned}{\boldsymbol {E}}&=-\nabla \phi _{e}-{\frac {\partial {\boldsymbol {A}}_{\mathrm {e} }}{\partial t}}-{\frac {1}{\varepsilon _{0}}}\nabla \times {\boldsymbol {A}}_{\mathrm {m} }\\{\boldsymbol {H}}&=-\nabla \phi _{m}-{\frac {\partial {\boldsymbol {A}}_{\mathrm {m} }}{\partial t}}+{\frac {1}{\mu _{0}}}\nabla \times {\boldsymbol {A}}_{\mathrm {e} }\end{aligned}}}
{
(
∇
2
−
1
c
2
∂
2
∂
t
2
)
ϕ
e
=
−
ρ
e
ε
0
(
∇
2
−
1
c
2
∂
2
∂
t
2
)
ϕ
m
=
−
ρ
m
μ
0
(
∇
2
−
1
c
2
∂
2
∂
t
2
)
A
e
=
−
μ
0
J
e
(
∇
2
−
1
c
2
∂
2
∂
t
2
)
A
m
=
−
ε
0
J
m
{\displaystyle {\begin{cases}{\begin{aligned}\left(\nabla ^{2}-{\dfrac {1}{c^{2}}}{\dfrac {\partial ^{2}}{\partial t^{2}}}\right)\phi _{\mathrm {e} }&=-{\dfrac {\rho _{\mathrm {e} }}{\varepsilon _{0}}}\\\left(\nabla ^{2}-{\dfrac {1}{c^{2}}}{\dfrac {\partial ^{2}}{\partial t^{2}}}\right)\phi _{\mathrm {m} }&=-{\dfrac {\rho _{\mathrm {m} }}{\mu _{0}}}\\\left(\nabla ^{2}-{\dfrac {1}{c^{2}}}{\dfrac {\partial ^{2}}{\partial t^{2}}}\right){\boldsymbol {A}}_{\mathrm {e} }&=-\mu _{0}{\boldsymbol {J}}_{\mathrm {e} }\\\left(\nabla ^{2}-{\dfrac {1}{c^{2}}}{\dfrac {\partial ^{2}}{\partial t^{2}}}\right){\boldsymbol {A}}_{\mathrm {m} }&=-\varepsilon _{0}{\boldsymbol {J}}_{\mathrm {m} }\end{aligned}}\end{cases}}}
磁気単極子は陽子 の
10
16
{\displaystyle 10^{16}}
磁荷
g
{\displaystyle g}
g
=
n
h
e
{\displaystyle g={\frac {n\mathrm {h} }{\mathrm {e} }}}
ここで
h
{\displaystyle \mathrm {h} }
プランク定数 、
e
{\displaystyle \mathrm {e} }
素電荷 、
n
{\displaystyle n}
ディラックの量子化 」と呼ぶ。
このとき磁荷
g
{\displaystyle g}
電磁場 から受ける力
F
{\displaystyle F}
F
=
g
(
H
−
v
×
D
)
{\displaystyle {\boldsymbol {F}}=g({\boldsymbol {H}}-{\boldsymbol {v}}\times {\boldsymbol {D}})}
と書ける[ 2]
この節ではアインシュタインの縮約記法 を断りなく用いる。またミンコフスキー計量 をdiag (−1, +1, +1, +1)としている。
まず粒子の運動と電磁場をローレンツ変換 に対して不変なテンソル で次のように表す。
4元速度 (英語版 ) [ 注 1]
(
v
0
,
v
1
,
v
2
,
v
3
)
=
(
−
c
1
−
v
2
/
c
2
,
v
x
1
−
v
2
/
c
2
,
v
y
1
−
v
2
/
c
2
,
v
z
1
−
v
2
/
c
2
)
{\displaystyle (v_{0},v_{1},v_{2},v_{3})=(-{\frac {c}{\sqrt {1-v^{2}/c^{2}}}},{\frac {v_{x}}{\sqrt {1-v^{2}/c^{2}}}},{\frac {v_{y}}{\sqrt {1-v^{2}/c^{2}}}},{\frac {v_{z}}{\sqrt {1-v^{2}/c^{2}}}})}
4元力 (英語版 ) [ 注 1]
(
f
0
,
f
1
,
f
2
,
f
3
)
=
(
f
⋅
v
1
−
v
2
/
c
2
,
f
x
1
−
v
2
/
c
2
,
f
y
1
−
v
2
/
c
2
,
f
z
1
−
v
2
/
c
2
)
{\displaystyle (f^{0},f^{1},f^{2},f^{3})=({\frac {{\boldsymbol {f}}\cdot {\boldsymbol {v}}}{\sqrt {1-v^{2}/c^{2}}}},{\frac {f_{x}}{\sqrt {1-v^{2}/c^{2}}}},{\frac {f_{y}}{\sqrt {1-v^{2}/c^{2}}}},{\frac {f_{z}}{\sqrt {1-v^{2}/c^{2}}}})}
4元電流密度
(
J
e
0
,
J
e
1
,
J
e
2
,
J
e
3
)
=
(
c
ρ
e
,
J
e
x
,
J
e
y
,
J
e
z
)
{\displaystyle (J_{\mathrm {e} }^{0},J_{\mathrm {e} }^{1},J_{\mathrm {e} }^{2},J_{\mathrm {e} }^{3})=(c\rho _{\mathrm {e} },J_{\mathrm {e} x},J_{\mathrm {e} y},J_{\mathrm {e} z})}
4元磁流密度
(
J
m
0
,
J
m
1
,
J
m
2
,
J
m
3
)
=
(
c
ρ
m
,
J
m
x
,
J
m
y
,
J
m
z
)
{\displaystyle (J_{\mathrm {m} }^{0},J_{\mathrm {m} }^{1},J_{\mathrm {m} }^{2},J_{\mathrm {m} }^{3})=(c\rho _{\mathrm {m} },J_{\mathrm {m} x},J_{\mathrm {m} y},J_{\mathrm {m} z})}
4元電磁ポテンシャル
(
A
e
0
,
A
e
1
,
A
e
2
,
A
e
3
)
=
(
ϕ
e
/
c
,
A
e
x
,
A
e
y
,
A
e
z
)
{\displaystyle (A_{\mathrm {e} }^{0},A_{\mathrm {e} }^{1},A_{\mathrm {e} }^{2},A_{\mathrm {e} }^{3})=(\phi _{\mathrm {e} }/c,A_{\mathrm {e} x},A_{\mathrm {e} y},A_{\mathrm {e} z})}
-
(
A
m
0
,
A
m
1
,
A
m
2
,
A
m
3
)
=
(
ϕ
m
/
c
,
A
m
x
,
A
m
y
,
A
m
z
)
{\displaystyle (A_{\mathrm {m} }^{0},A_{\mathrm {m} }^{1},A_{\mathrm {m} }^{2},A_{\mathrm {m} }^{3})=(\phi _{\mathrm {m} }/c,A_{\mathrm {m} x},A_{\mathrm {m} y},A_{\mathrm {m} z})}
電磁場テンソル [ 注 2]
(
F
01
,
F
02
,
F
03
,
F
23
,
F
31
,
F
12
)
=
(
E
x
/
c
,
E
y
/
c
,
E
z
/
c
,
B
x
,
B
y
,
B
z
)
{\displaystyle (F^{01},F^{02},F^{03},F^{23},F^{31},F^{12})=(E_{x}/c,E_{y}/c,E_{z}/c,B_{x},B_{y},B_{z})}
電磁場テンソルのホッジ双対 [ 注 2]
(
F
~
01
,
F
~
02
,
F
~
03
,
F
~
23
,
F
~
31
,
F
~
12
)
=
(
B
x
,
B
y
,
B
z
,
−
E
x
/
c
,
−
E
y
/
c
,
−
E
z
/
c
)
{\displaystyle ({\tilde {F}}^{01},{\tilde {F}}^{02},{\tilde {F}}^{03},{\tilde {F}}^{23},{\tilde {F}}^{31},{\tilde {F}}^{12})=(B_{x},B_{y},B_{z},-E_{x}/c,-E_{y}/c,-E_{z}/c)}
電磁場テンソルとそのホッジ双対は交代記号 ε (エディントンのイプシロン ) を用いて次のように結ばれる。
F
~
α
β
=
1
2
ε
α
β
μ
ν
F
μ
ν
,
F
~
α
β
=
−
1
2
ε
α
β
μ
ν
F
μ
ν
{\displaystyle {\tilde {F}}^{\alpha \beta }={\frac {1}{2}}\varepsilon ^{\alpha \beta \mu \nu }F_{\mu \nu },\;{\tilde {F}}_{\alpha \beta }=-{\frac {1}{2}}\varepsilon _{\alpha \beta \mu \nu }F^{\mu \nu }}
すると電磁場の方程式は次のように表される。
アンペール ・ガウス の法則
∂
α
F
α
β
=
−
μ
0
J
e
β
{\displaystyle \partial _{\alpha }F^{\alpha \beta }=-\mu _{0}J_{\mathrm {e} }^{\beta }}
ファラデー ・ガウス の法則
∂
α
F
~
α
β
=
−
1
c
J
m
β
{\displaystyle \partial _{\alpha }{\tilde {F}}^{\alpha \beta }=-{\frac {1}{c}}J_{\mathrm {m} }^{\beta }}
ローレンツ力 [ 注 1]
f
α
=
(
q
e
F
α
β
+
q
m
μ
0
c
F
~
α
β
)
v
β
{\displaystyle f^{\alpha }=\left(q_{\mathrm {e} }F^{\alpha \beta }+{\frac {q_{\mathrm {m} }}{\mu _{0}c}}{{\tilde {F}}^{\alpha \beta }}\right)v_{\beta }}
電磁ポテンシャルを用いた表現では次のようになる。
磁気単極子が存在するとき、磁性体 に磁場が加わるとループ電流による磁化 M e 磁気分極 P m 誘電体 に電場が加わると電荷の偏りによる 誘電分極 P e M m 媒質 の外から見れば等価であるものの媒質内部の電磁場は違っていて、荷電粒子を入射するなどして区別することができる。
そこで、媒質の影響を取り入れた現象論的な電磁場 E ' D ' B ' H '
E
′
=
E
+
M
m
,
D
′
=
E
+
P
e
B
′
=
B
+
P
m
,
H
′
=
H
+
M
e
{\displaystyle {\begin{alignedat}{2}{\boldsymbol {E}}'=&{\boldsymbol {E}}+{\boldsymbol {M}}_{\mathrm {m} },\quad &{\boldsymbol {D}}'=&{\boldsymbol {E}}+{\boldsymbol {P}}_{\mathrm {e} }\\{\boldsymbol {B}}'=&{\boldsymbol {B}}+{\boldsymbol {P}}_{\mathrm {m} },\quad &{\boldsymbol {H}}'=&{\boldsymbol {H}}+{\boldsymbol {M}}_{\mathrm {e} }\end{alignedat}}}
分極電荷、分極磁荷を除いた真電荷、真電流、真磁荷、真磁流をそれぞれ ρ ' e J ' e ρ' m , J ' m
{
∇
⋅
B
′
=
ρ
m
′
∇
×
E
′
=
−
(
∂
B
′
∂
t
+
J
m
′
)
∇
⋅
D
′
=
ρ
e
′
∇
×
H
′
=
J
e
′
+
∂
D
′
∂
t
{\displaystyle {\begin{cases}{\begin{aligned}\nabla \cdot {\boldsymbol {B}}'&=\rho _{\mathrm {m} }'\\\nabla \times {\boldsymbol {E}}'&=-\left({\dfrac {\partial {\boldsymbol {B}}'}{\partial t}}+{\boldsymbol {J}}_{\mathrm {m} }'\right)\\\nabla \cdot {\boldsymbol {D}}'&=\rho _{\mathrm {e} }'\\\nabla \times {\boldsymbol {H}}'&={\boldsymbol {J}}_{\mathrm {e} }'+{\dfrac {\partial {\boldsymbol {D}}'}{\partial t}}\end{aligned}}\end{cases}}}
となり、真空中と同じ形で表すことができる。
磁気単極子を磁場の中に封じ込め振動させることによって燃料物質の陽子崩壊 を誘発してエネルギー源として利用する、というアイデアがある。
重力理論の専門家ロバート・L・フォワード が『竜の卵』において、磁気単極子と原子核が結合した高密度の物質「モノポリウム」を登場させ、その重力場で中性子星の潮汐力から人間を守るというアイデアを詳細に描写している[ 3] 山本弘 の小説『サイバーナイト 』では、これとほぼ同じ原理であるとしたモノポール反応炉が、モジュール(人が乗り込むタイプのパワードスーツ )やジャンプドライブ(ワープ )といった作中のテクノロジーに必要な存在とされている[ 4]
他に、アニメ『宇宙戦艦ヤマト 』シリーズのOVA 『YAMATO2520 』では動力源としてモノポールエンジンが、5pb. とニトロプラス 製作の科学アドベンチャーゲーム『ROBOTICS;NOTES 』では、「モノポール」(という名前の物体(?))が「空から落ちて」くる。特撮テレビ番組『ウルトラマンガイア 』では、体内に磁気単極子N極を持つ「超巨大単極子生物 モキアン 」が、地球内部のマントル流動を誘発させようとした。
^ a b c 一般的な表現とは添字の上下が異なるので注意。
^ a b 反対称テンソル であり、省略された成分は
F
10
=
−
F
01
{\displaystyle F^{10}=-F^{01}}