RC回路

RC回路（英: RC circuit）は、抵抗器とコンデンサで構成され、電圧または電流で駆動される電気回路。RCフィルタ、RCネットワークとも。1つの抵抗器と1つのコンデンサから構成される一次RC回路は、最も単純なRC回路の例である。

概要

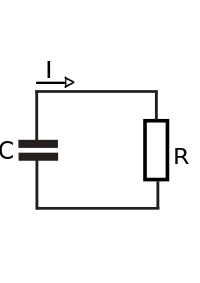RC回路

線形アナログ回路部品には、抵抗器（R）、コンデンサ（C）、コイル（L）がある。これらの組み合わせとしては、RC回路のほかにRL回路、LC回路、RLC回路が重要である（それぞれ、使っている部品の種類によって名前が付けられている）。多くのアナログ回路の重要な基本的特性はこれらの回路で示される。特に、これらの回路はパッシブフィルタとして機能する。本項目では、直列型と並列型のRC回路を扱う。

複素インピーダンス

静電容量$C$（ファラド）のコンデンサのインピーダンス$Z_{C}$（オーム）は次の式で表される。

$Z_{C}={\frac {1}{sC}}$

角周波数$s$は一般に複素数であり、次のように記述される。

$s\ =\ \sigma +j\omega$

ここで

• $j={\sqrt {-1}}$（虚数単位）
• $\sigma$は指数減少定数（ラジアン/秒）
• $\omega$は正弦波角周波数（ラジアン/秒）

正弦波定常状態

正弦波定常状態は、入力電圧が（指数減少成分がない）純粋な正弦波であるような特殊ケースを意味する。したがって

$\sigma \ =\ 0$

であり、$s$は次のように表せる。

$s\ =\ j\omega$

直列回路

直列RC回路

直列回路を分圧回路と見たとき、コンデンサにかかる電圧は以下のようになる。

$V_{C}(s)={\frac {1/Cs}{R+1/Cs}}V_{in}(s)={\frac {1}{1+RCs}}V_{in}(s)$

また、抵抗器にかかる電圧は以下のようになる。

$V_{R}(s)={\frac {R}{R+1/Cs}}V_{in}(s)={\frac {RCs}{1+RCs}}V_{in}(s)$

伝達関数

コンデンサの伝達関数は次のようになる。

$H_{C}(s)={V_{C}(s) \over V_{in}(s)}={1 \over 1+RCs}$

同様に抵抗器の伝達関数は以下の通りである。

$H_{R}(s)={V_{R}(s) \over V_{in}(s)}={RCs \over 1+RCs}$

極と零点

どちらの伝達関数にも1つの極が次の位置にある。

$s=-{1 \over RC}$

さらに、抵抗器の伝達関数には原点に零点がある。

利得と位相角

それぞれの部品における利得の大きさは以下の通り。

$G_{C}=|H_{C}(j\omega )|=\left|{\frac {V_{C}(j\omega )}{V_{in}(j\omega )}}\right|={\frac {1}{\sqrt {1+\left(\omega RC\right)^{2}}}}$

$G_{R}=|H_{R}(j\omega )|=\left|{\frac {V_{R}(j\omega )}{V_{in}(j\omega )}}\right|={\frac {\omega RC}{\sqrt {1+\left(\omega RC\right)^{2}}}}$

また、それぞれの位相角は次の通り。

$\phi _{C}=\angle H_{C}(j\omega )=\tan ^{-1}\left(-\omega RC\right)$
$\phi _{R}=\angle H_{R}(j\omega )=\tan ^{-1}\left({\frac {1}{\omega RC}}\right)$

これらの式をまとめて、出力を一般的なフェーザ表示で表すと次のようになる。

$V_{C}\ =\ G_{C}V_{in}e^{j\phi _{C}}$
$V_{R}\ =\ G_{R}V_{in}e^{j\phi _{R}}$

電流

この回路は直列回路なので、電流はどの箇所でも同じであり、次の式で得られる。

$I(s)={\frac {V_{in}(s)}{R+1/Cs}}={Cs \over 1+RCs}V_{in}(s)$

インパルス応答

各部品にかかる電圧のインパルス応答は、それぞれの伝達関数の逆ラプラス変換である。これは、入力電圧がインパルス（ディラックのデルタ関数）の時の回路の応答（出力）を表している。

コンデンサの電圧におけるインパルス応答は次の通り。

$h_{C}(t)={1 \over RC}e^{-t/RC}u(t)={1 \over \tau }e^{-t/\tau }u(t)$

ここで$u(t)$はヘヴィサイドの階段関数であり、

$\tau \ =\ RC$

は、時定数である。

同様に、抵抗器の電圧のインパルス応答は次の通りである。

$h_{R}(t)=\delta (t)-{1 \over RC}e^{-t/RC}u(t)=\delta (t)-{1 \over \tau }e^{-t/\tau }u(t)$

ここで$\delta (t)$はディラックのデルタ関数である。

周波数領域

回路の特性は周波数領域でも表現できる。周波数領域で解析することで、回路（フィルタ）がどの周波数を通過/除去するかを知ることができる。この解析は、周波数が非常に高くなるときや非常に低くなるときの利得がどうなるかを検討する際にも重要である。

$\omega \to \infty$となるとき:

$G_{C}\to 0$
$G_{R}\to 1$

$\omega \to 0$となるとき:

$G_{C}\to 1$
$G_{R}\to 0$

となる。

すなわち、コンデンサにかかる電圧を出力としたとき、高周波は減衰（除去）し、低周波は通過する。したがって、この回路は低周波濾波器として機能する。しかし、抵抗器にかかる電圧を出力とすると、高周波は通過し、低周波は除去される。この場合はこの回路が高周波濾波器として機能する。

フィルタが通過させる周波数の範囲を、そのフィルタの帯域幅という。フィルタによって信号の電力が本来の半分に減衰させられる周波数を遮断周波数と呼ぶ。そのとき、回路の利得は次のようになる。

$G_{C}=G_{R}={\frac {1}{\sqrt {2}}}$

この値を上掲の式に当てはめると

$\omega _{c}={\frac {1}{RC}}\ \mathrm {rad/s}$

または

$f_{c}={\frac {1}{2\pi RC}}\ \mathrm {Hz}$

となる。これがフィルタによって電力が本来の半分になる周波数である。

明らかに位相も周波数によって変化するが、一般に利得の変化ほど注目されない。

$\omega \to 0$となるとき:

$\phi _{C}\to 0$
$\phi _{R}\to 90^{\circ }=\pi /2^{c}$

$\omega \to \infty$となるとき:

$\phi _{C}\to -90^{\circ }=-\pi /2^{c}$
$\phi _{R}\to 0$

となる。

したがって、直流（0Hz）ではコンデンサの電圧は信号の電圧と位相が同じだが、抵抗器の電圧は位相が90°進む。周波数が高くなるにつれて、コンデンサの電圧の位相は信号の位相に対して90°遅れるようになっていき、抵抗器の電圧の位相は信号の位相と同じになっていく。

時間領域

本節ではネイピア数 e に関する知識を前提としている。

最も直接的に時間領域のふるまいを調べるには、上掲の$V_{C}$と$V_{R}$の式にラプラス変換を施せばよい。これにより実質的に$j\omega \to s$という変換がなされる。ステップ入力（$t=0$以前には$V_{in}=0$で、その後$V_{in}=V$となる入力）を与えると、

$V_{in}(s)=V{\frac {1}{s}}$
$V_{C}(s)=V{\frac {1}{1+sRC}}{\frac {1}{s}}$
$V_{R}(s)=V{\frac {sRC}{1+sRC}}{\frac {1}{s}}$

となる。

コンデンサ電圧のステップ応答

抵抗電圧のステップ応答

部分分数分解と逆ラプラス変換により、次が得られる。

$\,\!V_{C}(t)=V\left(1-e^{-t/RC}\right)$
$\,\!V_{R}(t)=Ve^{-t/RC}$

これらの式はコンデンサに電荷が蓄積されるときのコンデンサと抵抗器にかかる電圧を意味する。コンデンサが放電するときは式が全く逆になる。これは、$C=Q/V$ と $V=IR$ という関係（オームの法則）を使って電荷と電流で書き換えることもできる。

図に示されている通り、コンデンサにかかる電圧は時間経過とともに V に近づき、抵抗器にかかる電圧は 0 に近づいていく。これは、コンデンサが時間とともに電圧供給によって電荷を蓄えていき、最終的に完全に電荷を蓄えたときに開回路になるという直観的理解とも一致する。

これらの式は、直列RC回路に時定数があることを示し、それを一般に$\tau =RC$と表す。$\tau$はコンデンサにかかる電圧$V_{C}$が$V(1-1/e)$まで上がるのにかかる時間、および抵抗器にかかる電圧$V_{R}$が$V(1/e)$まで下がるのにかかる時間に対応している。

増減率は$\tau$当たり$\left(1-{\frac {1}{e}}\right)$である。したがって、$t=N\tau$から$t=(N+1)\tau$までの間に電圧は$t=N\tau$のときの電圧から最終的な電圧に向かって 63.2% 変化する。したがって、コンデンサへの電荷蓄積は$\tau$後には 63.2 % となり、約$5\tau$でほぼ完全に（99.3%）電荷を蓄積する。コンデンサが完全に電荷を蓄積した状態で電圧源を短絡回路に置き換えると、コンデンサにかかる電圧は$V$から 0 へ時間とともに指数関数的に低下していく。$\tau$後には電荷が 36.8% となり、約$5\tau$でほぼ完全に（0.7%）放電する。なお、回路に流れる電流$I$は、抵抗器にかかる電圧からオームの法則によって求めることができる。

以上のことは、回路を表した以下の微分方程式を解くことでも導き出すことができる。

${\frac {V_{in}-V_{C}}{R}}=C{\frac {dV_{C}}{dt}}$
$\,\!V_{R}=V_{in}-V_{C}$

1つめの方程式は積分因子を使って解くことができ、2つめはそこから容易に解ける。得られる解はラプラス変換を使って得られる解と全く同じである。

積分器

高い周波数でのコンデンサにかかる電圧を出力とする。高い周波数とは

$\omega \gg {\frac {1}{RC}}$

となるような周波数である。

これはつまり、コンデンサに電荷が蓄積されるのに十分な時間がないため、そこにかかる電圧も非常に小さいことを意味する。したがって、入力電圧は抵抗器にかかる電圧にほぼ等しい。これを示すため、次の電流$I$の式を考える。

$I={\frac {V_{in}}{R+1/j\omega C}}$

ここで、周波数についての条件は以下のようにも表せる。

$\omega C\gg {\frac {1}{R}}$

したがって

$I\approx {\frac {V_{in}}{R}}$となり、これは単なるオームの法則である。

ここで

$V_{C}={\frac {1}{C}}\int _{0}^{t}Idt$

であるから

$V_{C}\approx {\frac {1}{RC}}\int _{0}^{t}V_{in}dt$

となり、これはコンデンサにかかる電圧が一種の積分器となることを意味する。

微分器

低い周波数での抵抗器にかかる電圧を出力とする。低い周波数とは

$\omega \ll {\frac {1}{RC}}$

となるような周波数である。

この場合は、コンデンサは電荷を蓄積する時間があり、その電圧は入力電圧とほぼ等しくなる。再び電流$I$の式を考える。

$R\ll {\frac {1}{\omega C}}$

であるから

$I\approx {\frac {V_{in}}{1/j\omega C}}$
$V_{in}\approx {\frac {I}{j\omega C}}\approx V_{C}$

となる。したがって、抵抗器にかかる電圧は

$V_{R}=IR=C{\frac {dV_{C}}{dt}}R$
$V_{R}\approx RC{\frac {dV_{in}}{dt}}$

となり、これは抵抗器にかかる電圧が一種の微分器となることを意味する。

積分や微分をより正確にするには、オペアンプを使い、その入力やフィードバックループに抵抗器やコンデンサを適切に配置する必要がある。

並列回路

並列RC回路

並列RC回路は直列RC回路ほど興味深い性質を持たない。これは主に出力電圧$V_{out}$が入力電圧$V_{in}$と等しいためである。そのため、電流源を使って入力信号を与えない限り、この回路はフィルタとして機能しない。

複素インピーダンスを使ってそれぞれを流れる電流を表すと、

$I_{R}={\frac {V_{in}}{R}}\,$
$I_{C}=j\omega CV_{in}\,$

となる。

以上から明らかなように、コンデンサの電流は抵抗器（および入力）電流から90°位相がずれている。代わりに制御微分方程式を使って表すと次のようになる。

$I_{R}={\frac {V_{in}}{R}}$
$I_{C}=C{\frac {dV_{in}}{dt}}$

ステップ入力（実質的な0Hzまたは直流信号）を与えると、入力の微分は$t=0$でインパルスとなる。したがって、コンデンサは急速に電荷が蓄積され、回路が切れた状態になる。

関連項目

• 電気回路
• 積分回路、積分器
• 微分器

外部リンク

• RC Filter Calculator