ハイパスフィルタ

(実際にはこのような周波数特性は取れない)

ハイパスフィルタ(英語: High-pass filter: HPF)とは、フィルタの一種で、なんらかの信号のうち、遮断周波数より高い周波数の成分はほとんど減衰させず、遮断周波数より低い周波数の成分を逓減させるフィルタである。ローカットフィルタ等と呼ぶ場合もある。電気回路・電子回路では、フィルタ回路の一種である。日本語では「高域通過濾波器」とも言われる。オーディオでは「bass-cut filter」または「rumble filter」とも称する。
ハイパスフィルタはローパスフィルタと対称の関係にある。こういったフィルタには他にバンドパスフィルタとバンドストップフィルタがある。
伝達関数[編集]
連続時間のフィルタは、入出力の利得と位相の特性をラプラス変換を使用して伝達関数で表すことができる。
ハイパスフィルタの伝達関数は、
となる。ここで、 はラプラス変換の変数であり、 τ はフィルタの時定数、 K は通過域での利得である。
回路例[編集]
CとRを用いた回路[編集]

最も簡単なハイパスフィルタは、入力信号に並列する抵抗器と入力信号と直列するコンデンサから成り立っている。抵抗値と容量値の積(R×C)は時定数(τ)といい、遮断周波数に逆比例する。また、遮断周波数の信号を入力したとき、出力電圧は入力電圧の半分になる(−3dB)。遮断周波数f[Hz]、時定数τ[s]、抵抗値R[Ω]、容量値C[F]の関係は以下の式のようになる。
- 入力電圧値
- |Vin| [V]
- 出力電圧値
- |Vout| [V]
- 角周波数
- ω[rad](=2πf)
- コンデンサ・キャパシタ容量値
- C [F]
- 抵抗値
- R [Ω]
とした場合、
電圧利得の周波数特性は
ただし、[dB]として表すのが一般的である。
位相のずれの周波数特性は
となる。なお、この場合、θの単位は[rad](ラジアン)である。
オペアンプを用いた回路[編集]
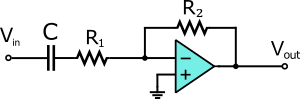
オペアンプを用いた1次のハイパスフィルタの回路図を右に示す。 この場合、通過域の利得は
で表され、遮断周波数は、
となる。
応用例[編集]
スピーカーにおいて、ツイーターにおける干渉もしくは破損を防ぐため、低域をブロックするために使われる。オーディオにおいて、パワーアンプより前で分離するためのフィルタ装置をチャネルディバイダ、パワーアンプの後、スピーカの直前で分離するものをネットワークと称する。 ほとんどのハイパスフィルタは直流(0Hz)ではゼロ利得となる。この特徴を利用し、交流信号に直流が重畳した信号(オフセットのある信号)から、オフセットを取り除くために使われるハイパスフィルタを「DC blocking filter」と呼ぶ。








