インパルス応答
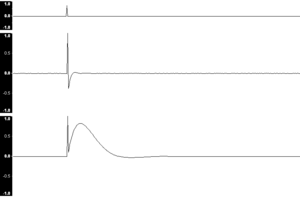
インパルス応答(インパルスおうとう、英語: impulse response)とは、インパルスと呼ばれる非常に短い信号を入力したときのシステムの出力である。インパルス反応とも。インパルスとは、時間的幅が無限小で高さが無限大のパルスである。実際のシステムではこのような信号は生成できないが、理想化としては有益な概念である。
LTIシステム(線形時不変系)と呼ばれるシステムは、そのインパルス応答によって完全に特徴付けられる。
数学的基礎[編集]
数学的には、インパルスはディラックのデルタ関数でモデル化される。T を(離散)システムとし、入力として x[n] をとり、y[n] という出力を生成するものとする。
したがって、T は(整数の)並びに作用して、別の並びを生成する作用素である。T はシステムそのものではなく、システムを数学的に表したものであることに注意が必要である。次のような T は非線形である。
また、次の場合は線形である。
T が線形であるとする。すると次が成り立つ。
また、次も成り立つ。
また、T が であるとき となるような変換について不変であるとする。このようなシステムでは、入力から得られる出力を計算で求めることができ、インパルス応答と呼ばれる特殊な並びでそのシステムの特性を完全に表すことができる。これは、次のように示すことができる。次の恒等式がある。
この両辺に T を作用させる。
もちろん、この式は以下の項が T の定義域にある場合のみ意味がある。
ここで、T は線形で、かつ変換に対して不変であるから、次のように書き換えられる。
出力 y[k] は次のように与えられる。
したがって、次のように書くことができる。
ここで
のように置くと、最終的に次の式が得られる。
は T で表されるシステムのインパルス応答である。上記からわかるように、h[n] は入力が離散的なディラックのデルタ関数であった時のシステム出力である。連続的な時間系でも、同様の結果が成り立つ。
概念的な例として、ある部屋の中に風船があり、その位置を p とする。風船が弾むと、「ぽん」という音がする。ここで、この部屋は「ぽん」という音を入力として多重反射させるシステム T である。入力 は「ぽん」であり、時間的幅が短いのでディラックのデルタ関数に似ている。出力 h[n,p] は残響の並びである。h[n,p] は風船の位置(p)に依存する。部屋の中のあらゆる位置 p について h[n,p] が判っていれば、我々はこの部屋のインパルス応答を把握していることになる。すると、その部屋が生成する音がどうなるかを常に予測することが可能となる。
数学的応用[編集]
数学においては、線型写像のインパルス応答は、写像におけるディラックのデルタ関数の像である。
インパルス応答関数のラプラス変換は、伝達関数として知られている。一般に、インパルス応答関数よりも伝達関数を使ってシステムを解析するほうが容易である。システムの出力のラプラス変換は、複素平面上(周波数領域)で伝達関数と入力関数の積を求めることで決定される。この結果に逆ラプラス変換を施すと、時間領域における出力関数が得られる。
時間領域で出力関数を直接決定するには、入力関数とインパルス応答関数の畳み込みが必要となる。これには積分が必要となり、周波数領域で2つの関数の単なる積を求めるよりも難しい。
実用[編集]
実際のシステムでは、テスト用の入力として完全なインパルスを生成するのは不可能である。したがって、インパルスの近似として短いパルスを使う。そのパルスがインパルス応答に比較して短ければ、その結果は理論上のインパルス応答に十分近いと言える。
スピーカー[編集]
1980年代にスピーカーのインパルス応答評価法が開発され、スピーカーの設計が大いに進歩した。スピーカーでは位相歪みが問題となる。これは、周波数特性のような測定可能な一般的特性とは異なる問題である。位相歪みは、共振、コーンにおけるエネルギー蓄積、スピーカー躯体の振動などによって発生する微妙な音の遅延が原因で発生する。位相歪みは音をにじませ(スミアー)、透明感がなくなる原因となる。インパルス応答を測定すると、その時間スミアーが分かるので、コーンや躯体の材質や形状の改良などに使うことで歪みを低減させることが可能となった。当初、短いパルスを使っていたが、システムの線形性を維持するには振幅を大きくできず、結果として出力も小さくなるため、ノイズとの識別が困難だった。その後、M系列のような入力を使うようになり、コンピュータを使ってそこからインパルス応答を求めるようになった。最近では、周波数ごとの遅延応答を図示できるようになっている。その応用としてホールなどの残響を測定し、音響設計をする手段としても用いられる。
デジタルフィルタ[編集]
インパルス応答は、音響処理におけるデジタルフィルタの設計で非常に重要である。デジタルフィルタは耳障りなプレエコーを生成することが多いためである。
電子工学的処理[編集]
インパルス応答解析は、レーダー、超音波検査、その他のデジタル信号処理でも重視される。興味深い例としてブロードバンドインターネット接続がある。電話回線では4kHzの音声信号(あるいはモデムを使って300bit/sのデータ)しか送れなかったが、現在では同じ回線で2Mb/sが可能となっている。これは、回線上で発生するエコーやスミアーを消し去る適応フィルタによるところが大きい。
制御システム[編集]
制御理論では、インパルス応答はディラックのデルタ関数の入力への応答特性である。これは力学系の解析に有効である。デルタ関数をラプラス変換すると1になるので、インパルス応答はシステムの伝達関数の逆ラプラス変換と等価になる。

![{\displaystyle y\left[n\right]=T\left[x\left[n\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/961a3a1d05ccd51e9e745cccba0587316bcea35c)
![{\displaystyle T\left[x\left[n\right]\right]=x^{2}\left[n\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff343f065eb62e3fb28540132ee7d31fc6b54517)
![{\displaystyle T\left[x\left[n\right]\right]=x\left[n-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6497a9f44ac48336346e200f45ae38eca594ba7)
![{\displaystyle T\left[x\left[n\right]+y\left[n\right]\right]=T\left[x\left[n\right]\right]+T\left[y\left[n\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bb10e1490efed5d3cb2cb8ab77b18830016ea94)
![{\displaystyle T\left[\lambda x\left[n\right]\right]=\lambda T\left[x\left[n\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63fdebe8fbf006f78b0e66957516e61c4a862a6f)
![{\displaystyle y\left[n-k\right]=T\left[x\left[n-k\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cc23b07dde0c70a34f6659e15e007f9d168d056)
![{\displaystyle x\left[n\right]=\sum _{k}x\left[k\right]\delta \left[n-k\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e66c6823c79306bddc3b22dd65a2ff1167711c5)
![{\displaystyle T\left[x\left[n\right]\right]=T\left[\sum _{k}x\left[k\right]\delta \left[n-k\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f508325ee76dd413eb06138c6e482b1cdc7f0c06)
![{\displaystyle \sum _{k}x\left[k\right]\delta \left[n-k\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f0e6c16d2800fe348dfe9b4cc4a1170e5ebecf3)
![{\displaystyle T\left[x\left[n\right]\right]=\sum _{k}x\left[k\right]T\left[\delta \left[n-k\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/728cee592f6bdfaa7cd5eb88772e25273545c66c)
![{\displaystyle y\left[k\right]=T\left[x\left[k\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe69e082b8b2f9d45a67add6f059606cf956770e)
![{\displaystyle y\left[n\right]=\sum _{k}x\left[k\right]T\left[\delta \left[n-k\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/370368ee80b3aa1f901d8054b3dcfed3b6454792)
![{\displaystyle h\left[n-k\right]=T\left[\delta \left[n-k\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73f14d5e48430f542d820689030f0f2499972a15)
![{\displaystyle y\left[n\right]=\sum _{k}x\left[k\right]h\left[n-k\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60cda1b57b2b9c701ea3d7a3f69cee5c77da0e0b)
![{\displaystyle h\left[n\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb4920cd26625cc4532f981c9ac79942d0efca00)
![{\displaystyle \delta _{p}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b43984c026505cf71fb99f31395cfa2ac6d93508)