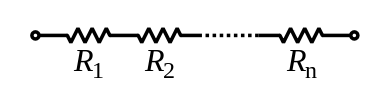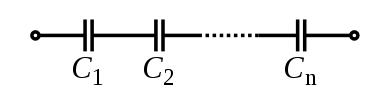| この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)
出典検索?: "直列回路と並列回路" – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2014年5月) |
 2つの抵抗器による直列回路(左)と並列回路(右)。電流計と電圧計も接続されている。
2つの抵抗器による直列回路(左)と並列回路(右)。電流計と電圧計も接続されている。
直列回路(ちょくれつかいろ、英語:series circuits)と並列回路(へいれつかいろ、英語:parallel circuits)とは、電子回路や電気回路の回路構成である。
電子部品の回路上の接続方法には直列(series)と並列(parallel)がある。2つの端子を持つ部品を数珠繋ぎに接続した回路を直列回路(series circuit)、2つの端子をそれぞれ互いに接続した回路を並列回路(parallel circuit)と呼ぶ。直列回路では、電流の経路が1つであり、同じ電流が各部品を順に流れる。並列回路では、電流の経路が分岐して各部品に同じ電圧がかかる。
例えば、2つの豆電球と電池を使った簡単な回路を考えてみる。電池から伸びた導線が1つの豆電球に接続され、そこから次の豆電球に接続され、最終的に電池に戻るという回路構成は直列回路である。電池から2本の導線が伸びて、それぞれ別の豆電球に繋がり、そこからまた別々に電池に戻る場合、回路構成は並列回路となる。
直列回路[編集]
直列回路は、カスケード結合(cascade-coupled)またはデイジーチェイン結合(daisychain-coupled)とも呼ばれる。キルヒホッフの法則より、直列回路に入った電流は回路内の全部品を流れることになる。つまり、直列回路上の各部品を流れる電流は同じである。また、全部品の電圧降下の合計は、個々の部品の電圧降下を加算したものとなる。
直列回路上の全部品の電気抵抗の合計は、個々の部品の電気抵抗値を加算したものとなる。
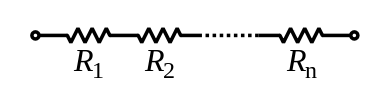

ここで、 、
、 などは直列接続された抵抗器である。オームの法則によれば、電流
などは直列接続された抵抗器である。オームの法則によれば、電流  は以下のようになる。
は以下のようになる。

個々の抵抗器  にかかる電圧は、再度オームの法則を使って次のようになる。
にかかる電圧は、再度オームの法則を使って次のようになる。

ここで  は上で求められた電流である。各抵抗器には抵抗値に比例した電圧がかかる。従って抵抗器が2つの場合、次のような関係が成り立つ。
は上で求められた電流である。各抵抗器には抵抗値に比例した電圧がかかる。従って抵抗器が2つの場合、次のような関係が成り立つ。

コイル[編集]
コイルも同様の法則に従い、コイルの直列回路でのインダクタンスの合計は個々のコイルのインダクタンスを全て加算した値となる。


しかし、部品配置によっては隣接するコイルの磁場が互いに影響しあうことを防げない場合もある。この相互作用を相互インダクタンス M で表す。例えば、2つのコイルを直列接続した場合、全体のインダクタンスは以下のいずれかとなる。

または

どちらになるかは互いの磁場がどう影響しあうかによる。
コイルが2つより多くなると、それぞれのコイル間の相互インダクタンスによって計算が複雑化する。コイルが3つの場合、相互インダクタンスは  、
、  、
、  の3つになり、全体のインダクタンスを表す式は8種類になる。
の3つになり、全体のインダクタンスを表す式は8種類になる。
コンデンサ[編集]
コンデンサは異なる法則に従う。コンデンサの直列回路の静電容量は、個々のコンデンサの静電容量の逆数の総和の逆数となる。
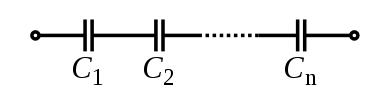
 .
.
並列回路[編集]
並列回路では、各部品にかかる電圧は同じ大きさで同じ方向になる。従って、全部品に同じ電圧変数を使う。全体を流れる電流は、キルヒホッフの法則より個々のループを流れる電流の総和である。オームの法則から、電圧を括りだすと次のような式になる。


式を簡略化するため、並列性を表現するのに垂直な2本の平行線  を使う。例えば、2つの抵抗器なら次のようになる。
を使う。例えば、2つの抵抗器なら次のようになる。
 .
.
電子回路の参考書によっては、斜め線を2本用いた「//」を並列回路の記号として用いることがある。

全部品の電気抵抗の総和は、個々の抵抗器の抵抗値  の逆数の総和の逆数である。
の逆数の総和の逆数である。
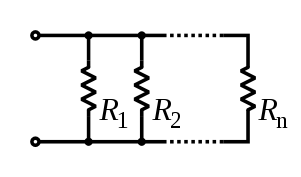

ある抵抗  に流れる電流は、オームの法則により次のようになる。
に流れる電流は、オームの法則により次のようになる。

各抵抗器には抵抗値の逆数に比例した電流が流れるので、2つの抵抗器がある場合、次のような関係が成り立つ。

コイル[編集]
コイルも同様で、全体のインダクタンスは個々のコイルのインダクタンスの逆数の総和の逆数である。

 .
.
コイル同士の磁場の相互作用がある場合、相互インダクタンスがあるため、この式には従わない。2つのコイルの相互インダクタンスを M としたとき、全体のインダクタンスは次のようになる。

 の場合、次のようになる。
の場合、次のようになる。

 の符号は互いの磁場の向きに依存する。2つの同じコイルを密結合した場合、全体のインダクタンスは1つのコイルのインダクタンスと等しくなる(M が L にほぼ等しくなる)。また、磁場の向きが互いを打ち消すようになっている場合、全体のインダクタンスはゼロになる。
の符号は互いの磁場の向きに依存する。2つの同じコイルを密結合した場合、全体のインダクタンスは1つのコイルのインダクタンスと等しくなる(M が L にほぼ等しくなる)。また、磁場の向きが互いを打ち消すようになっている場合、全体のインダクタンスはゼロになる。
2つより多くのコイルでは、それぞれのコイル間の相互インダクタンスが発生するため、全体のインダクタンスの計算は複雑になる。3つのコイルの場合、  、
、  、
、  という相互インダクタンスが発生する。これは
という相互インダクタンスが発生する。これは  行列の逆行列の項の総和で計算される(この場合は 3 × 3 の行列)。
行列の逆行列の項の総和で計算される(この場合は 3 × 3 の行列)。
このときの関係方程式は次の形式となる。

コンデンサ[編集]
コンデンサは異なる法則に従う。並列回路での全体の静電容量は個々のコンデンサの静電容量の単純な総和である。
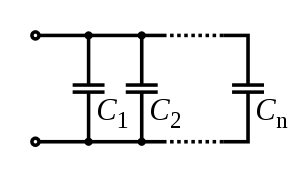

並列回路での定格電圧は、個々のコンデンサのうち定格電圧が最も小さいものによって制限される。
関連項目[編集]
外部リンク[編集]