フェルミエネルギー
量子力学や物性物理学においてフェルミエネルギー (Fermi energy)あるいはフェルミ準位(Fermi level)とは、相互作用のないフェルミ粒子系(理想フェルミ気体)の絶対零度での化学ポテンシャル(または電気化学ポテンシャル)µのことであり、通常と表される[1]。
フェルミエネルギーは量子統計力学、物性物理学、半導体物理学[2] などの分野で用いられる。
フェルミエネルギーとフェルミ準位は通常区別される.
呼び方について
[編集]半導体工学などでは、有限温度の理想フェルミ気体の化学ポテンシャルについても「フェルミエネルギー(またはフェルミ準位)」と呼ぶこともある。
また「フェルミエネルギー」と「フェルミ準位」は同義語として扱うことが多いが、理想フェルミ気体の化学ポテンシャルを、絶対零度では「フェルミエネルギー」、有限温度では「フェルミ準位」と区別して呼ぶこともある。このように定義した場合、絶対零度でフェルミ準位とフェルミエネルギーは等しくなる。
フェルミエネルギーでの占有数
[編集]
熱力学的平衡にある理想フェルミ気体において、エネルギーが E である準位を占有するフェルミ粒子の個数の統計的期待値は、次のフェルミ分布で表される[3]。
ここで T は温度、k はボルツマン定数、 μ は化学ポテンシャルである。分布のプロットを右図に示す。f が 1 に近づくほど、この状態が占有される確率は高くなる。f が 0 に近づくほど、この状態が空になる確率は高くなる。
絶対零度(基底状態)では、フェルミ分布は階段関数になり、その不連続点がフェルミエネルギーである。
フェルミエネルギー EF にエネルギー準位が存在する場合、 EF は絶対零度での占有数の統計的期待値が1/2になるエネルギー準位に等しく、「絶対零度での電子の占有確率が1/2になるエネルギー」とも言われる[4]。フェルミ準位に状態があれば (ε = µ)、その状態は50%の占有される確率を持つ。
またフェルミエネルギー EF にエネルギー準位が存在しない場合、フェルミエネルギーより高いエネルギー準位の絶対零度での占有数が0であることがわかる。よってフェルミエネルギーは「絶対零度におけるフェルミ粒子によって占められた準位のうちで最高の準位のエネルギー」とも言える[5]。ただしフェルミエネルギーに準位が存在しない場合、最も高いエネルギーを持つ粒子のエネルギーとフェルミエネルギーは一致しなくなる。半導体や絶縁体の場合がこれに相当する。
井戸型ポテンシャル中の自由電子
[編集]1次元の場合
[編集]一辺がLである箱の中にN個のフェルミ粒子(スピン1/2)があるときを考える。 この場合を表すモデルは、1次元の無限に深い長さLの井戸型ポテンシャルである。 この井戸型ポテンシャル中のフェルミ粒子のエネルギー準位は量子数nでラベル付けされる。
ここではフェルミ粒子が箱から受けるポテンシャルエネルギーである。
それぞれのエネルギー準位でスピン1/2(上向きスピン)と−1/2(下向きスピン)という異なる2つの状態が可能であるため、2つの粒子が同じエネルギーを占有することができる。しかしパウリの排他原理により、3つ以上の粒子は同じエネルギーを占有できない。絶対零度(基底状態)では全エネルギーが最低である電子配置をとり、n = N/2までの全てのエネルギーは占有され、n = N/2よりエネルギーが高い準位は全て空である。
フェルミエネルギーの基準をとなるように定義すると、奇数個の電子(N − 1)または偶数個の電子(N)のフェルミエネルギーは次のように与えられる。
3次元の場合
[編集]ここで一辺が長さLである3次元立方体の箱を考える(無限に深い井戸型ポテンシャルを参照)。 これは金属中の電子を記述するのに良いモデルとなる。
ここで状態は3つの量子数 nx, ny,nzでラベル付けされている。 1粒子エネルギーは、
nx, ny, nzは正の整数、mはフェルミ粒子(この場合は電子)の質量である。同じエネルギーをもつ複数の状態がある(たとえば)。N個の相互作用のないスピン1/2のフェルミ粒子をこの箱に入れる。このフェルミエネルギーを計算するために、Nが大きい場合を見てみる。
ベクトルを導入すると、それぞれの量子状態はエネルギー
をもつn空間の点に対応する。 は通常のユークリッド長さの二乗を表す。 エネルギーがEF + E0以下の状態の数は、 EF + E0が正であるn空間の領域での半径の球の中にある状態の数に等しい。 基底状態におけるこの数は、系のフェルミ粒子の数に等しい。

2つのスピン状態があるため因子2がつき、全てのnが正である領域には球の1/8だけがあるため、因子1/8がつく。 よって
よってフェルミエネルギーは次式で与えられる。
これから(L2 をV2/3に置き換えると)フェルミエネルギーは体積あたりの粒子数(個数密度)で決まることがわかる。
個のフェルミ粒子のフェルミ球の全エネルギーは次式で与えられる。
よって電子の平均エネルギーは次のように与えられる。
3次元の等方的な場合のフェルミ面は、フェルミ球として知られる。
任意の次元の場合
[編集]次元の体積積分を使うと、状態密度は、
粒子数を求めることにより、フェルミエネルギーを抽出できる。
よって
ここでは内部ヒルベルト空間の次元であり、スピンの場合は2である。
バンド構造
[編集]
固体のバンド理論では、電子のエネルギー固有状態はバンド構造を形成する。結晶中の電子のエネルギーはバンド構造を形成する。電子はバンド構造中の1粒子エネルギー固有状態 ε を占有する。この1粒子描像は近似ではあるが、電子のふるまいの理解を容易にし、正しく適用すれば一般的に正しい結果を与える。
物質のバンド構造中の EF の位置は、電子のふるまいを決定する上で重要となる。フェルミ準位は現実のエネルギー準位に必ずしも対応しておらず(絶縁体でのフェルミ準位はバンドギャップの中にある)、バンド構造の存在も必要としない。
金属中の電子
[編集]金属中の自由電子模型では、金属中の電子はフェルミ気体を作ると考えることができる。金属のフェルミエネルギーは、絶対零度の金属中の電子をバンドの底から詰めていき、その数が系の全電子数になったところの電子のエネルギーである。
金属や半金属、縮退半導体では、 EF は非局在バンドの中にある。 EF 近くの多数の状態は熱的に活性で、容易に電流を運ぶ。
金属の伝導電子の数密度はおよそ1028から1029 electrons/m3であり、通常の固体物質での原子の典型的な密度でもある。 この数密度からフェルミエネルギーを求めると、次のオーダーになることがわかる。
半導体・絶縁体中の電子
[編集]半導体や絶縁体の場合、フェルミエネルギーが伝導帯と価電子帯の間のバンドギャップの中にあり、エネルギー準位が存在しない。よって金属などでは成り立っていた「フェルミエネルギー = フェルミ粒子が占有している最も高いエネルギー準位」は、半導体・絶縁体では成り立たない。またフェルミエネルギーでのフェルミ分布関数の値1/2に、占有数の期待値という意味は無い。
真性半導体のフェルミエネルギーは、伝導帯のエネルギー、価電子帯のエネルギー、有効状態密度、を用いて次のように表される。
この第2項目は小さく、バンドギャップのほぼ中央に位置する。
非縮退半導体のフェルミエネルギーEFは、真性キャリア密度、伝導帯の電子密度、価電子帯の正孔密度を用いて次のように表せる[6]。
ドープ量が多いほど、フェルミエネルギーの位置はバンド端の近くになる。
絶縁体では、 EF は大きなバンドギャップの中にあり、電荷担体の存在しうる(有限の状態密度を持つ)バンドから遠く離れている。
半導体や半金属においてバンド構造に対する EF の位置は、ドーピングやゲーティングによってかなりの程度コントロールすることができる。これらのコントロールは電極によって固定されている EF を変えるわけではなく、全体のバンド構造を上下している(時にはバンド構造の形も変える)。半導体のフェルミ準位についての詳細は、[7] などを参照。
関連する量
[編集]このフェルミエネルギーの定義を使うと、様々な関連する量が有用になりえる。
フェルミ温度は次のように定義される。
フェルミ温度は、フェルミ統計に関連する量子的効果に熱的効果が匹敵する場合の温度として考えることができる[8]。 金属のフェルミ温度は室温より何桁も大きい。
その他の量としてフェルミ運動量とフェルミ速度がある。
ここでは電子の質量である。 これらの量はそれぞれ、フェルミ面でのフェルミ粒子の運動量と群速度である。 フェルミ運動量はとして書くこともできる。 ここではフェルミ球の半径であり、フェルミ波数ベクトルと呼ばれる[9]。
これらの量は、フェルミ面が球でない場合にはwell-definedではない。 上述のような2次の分散関係の場合は[10] を参照。
局所伝導帯基準、内部化学ポテンシャル、パラメータ ζ
[編集]バンド端のエネルギー εC に対して測定された電子エネルギー準位を示すために記号 ℰ を使うこととすると、一般的に ℰ = ε – εC を得る。また、パラメータ ζ [11] をバンド端を基準としたフェルミ準位 ζ = μ – εC と定義する。
すると、フェルミ分布関数は次のように書ける。
金属のバンド理論は、その基礎にある熱力学と統計力学に多大な注意を払ったゾンマーフェルトが1927年に発展させた。紛らわしいがいくつかの文脈ではバンド基準量 ζ は「フェルミ準位」「化学ポテンシャル」「電気化学ポテンシャル」と呼ばれ、大域的に基準を決めたフェルミ準位の曖昧さにつながる。この記事では ζ を示すために「伝導帯基準フェルミ準位」や「内部化学ポテンシャル」という言葉を使うことにする。
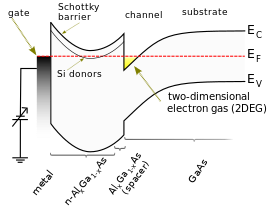
ζ は活性な電荷キャリアの数とその運動エネルギーと直接的に関係している。よってそれらは(電気伝導率など)物質の局所的特性に直接関与している。このため単一で均一な導電性物質での電子の特性に集中するとき、ζ の値に焦点を当てるのが一般的である。自由電子のエネルギー状態との類似性より、状態の ℰ はその状態の運動エネルギーであり、εC はポテンシャルエネルギーである。この点を考慮して、パラメータ ζ は「フェルミ運動エネルギー」と名前をつけることもできる。
μ とは違い、熱平衡状態においてもパラメータ ζ は物質中で一定ではない。εC は物質の質や不純物/ドーパントのような因子によって変化するため、物質中の位置によって μ は異なる。半導体や半金属の表面近くでは、電界効果トランジスタのように、ζ は外部から加えられた電場によって強く支配される。マルチバンド材料では、ζ は単一の場所でも複数の値をとり得る。たとえばアルミニウム金属片では、フェルミ準位を横切る2つの伝導バンドが存在する(その他の材料では更に多くバンドが存在する)[12]。各バンドに対応してそれぞれ異なるバンド端エネルギー εC と異なる ζ が存在する。
絶対零度での ζ の値は広くフェルミエネルギーと呼ばれており、ζ0 と書くことがある。しかし、紛らわしいことに「フェルミエネルギー」という言葉が絶対零度でないときの ζ を示すときに使われることもある。
フェルミ準位と電圧
[編集]
フェルミ準位の差は電圧計で簡単に測定することができる。
電流は静電ポテンシャル(ガルバニ電位)の差が駆動力であると言われることがあるが、厳密には正しくない[13]。その反例として、pn接合などのマルチ材料デバイスは平衡において内部静電ポテンシャル差を持っているが正味の電流は生じず、電圧計を接続しても 0 V である[14]。明らかに静電ポテンシャルは物質中の電荷の流れを決める因子の一つに過ぎず、パウリ反発、キャリア濃度勾配、電磁誘導、熱的効果なども重要な役割を果たしている。
実際、電子回路で測定される「電圧」と呼ばれる量は、電子の化学ポテンシャル(フェルミ準位)と単純な関係にある。電圧計のリード線が回路中の2点に接続されたときに表示される電圧は、単位電荷が一方の点からもう一方の点に移動したときに移動する「全」仕事の測定値である。単純なワイヤーが電圧の異なる2点間に接続されたとき(短絡が起きる)、電圧が正から負の方向に電流が流れ、仕事が熱に変換される。
物質のフェルミ準位は、電子をつけ加えるのに必要な仕事、または電子を取り除いたときに得られる仕事を表す。よって電子回路中の2点 A, B 間の測定される電圧差 VA − VB は、フェルミ準位で対応する化学ポテンシャル差 µA − µB と次の式で厳密に関係づけられる[15]。
ここで e は電気素量。
上記の議論から、電子は単純な経路が与えられたとき µ が高い点(低電圧)から低い点(高電圧)に移動することがわかる。この電子の流れは、低い µ を(帯電またはその他の反発効果により)増加させ、同様に高い µ を低下させる。その結果、2つの物質の µ は同じ値に落ち着く。このことは、次の電子回路の平衡状態に関する重要な事実を与える。
このことは、平衡状態では(電圧計で測定される)2点間の電圧はゼロであることも意味している。ここでの熱力学的平衡は、回路が内部で接続されており、バッテリーやその他の電源を含んでおらず、温度の変動も無い必要があることに注意。
関連用語
[編集]関連項目
[編集]出典
[編集]- ^ Kittel, Charles. Introduction to Solid State Physics, 7th Edition. Wiley
- ^ 例:Electronics (fundamentals And Applications) by D. Chattopadhyay, Semiconductor Physics and Applications by Balkanski and Wallis.
- ^ Kittel, Charles; Herbert Kroemer (1980-01-15). Thermal Physics (2nd Edition). W. H. Freeman. p. 357. ISBN 978-0-7167-1088-2
- ^ タウア・ニン 最新VLSIの基礎 第2版, Yuan Taur・Tak H. Ning・芝原健太郎・宮本恭幸・内田建, 丸善出版, 2013年1月.
- ^ 第8版 キッテル固体物理学入門, Charles Kittel・宇野良清・津屋昇・新関駒二郎・森田章・山下次郎, 丸善出版, 2005年12月.
- ^ B.L.アンダーソン、R.L.アンダーソン 著、樺沢宇紀 訳『半導体デバイスの基礎』 上巻(半導体物性)、丸善出版、2012年。ASIN 462106147X。ISBN 9784621061473。
- ^ Sze, S. M. (1964). Physics of Semiconductor Devices. Wiley. ISBN 0-471-05661-8
- ^ “Introduction to Quantum Statistical Thermodyamics”. Utah State University Physics. 23 April 2014閲覧。[リンク切れ]
- ^ Ashcroft, Neil W.; Mermin, N. David (1976). Solid State Physics. Holt, Rinehart and Winston. ISBN 0-03-083993-9
- ^ Fermi level and Fermi function, from HyperPhysics
- ^ Sommerfeld, Arnold (1964). Thermodynamics and Statistical Mechanics. Academic Press
- ^ “3D Fermi Surface Site”. Phys.ufl.edu (1998年5月27日). 2013年4月22日閲覧。
- ^ I. Riess, What does a voltmeter measure? Solid State Ionics 95, 327 (1197) [1]
- ^ Sah, Chih-Tang (1991). Fundamentals of Solid-State Electronics. World Scientific. p. 404. ISBN 9810206372
- ^ Datta, Supriyo (2005). Quantum Transport: Atom to Transistor. Cambridge University Presss. p. 7. ISBN 9780521631457
参考文献
[編集]- Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2nd ed.). W. H. Freeman Company. ISBN 0-7167-1088-9
- Table of Fermi energies, velocities, and temperatures for various elements.



















































