デバイ模型
| 統計力学 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|

| ||||||||||||
| 熱力学 · 気体分子運動論 | ||||||||||||
| ||||||||||||
デバイ模型(デバイもけい、英: Debye model)とは熱力学と固体物理学において、固体におけるフォノンの比熱(熱容量)への寄与を推定する手法である。1912年にピーター・デバイにより考え出された[1]。デバイ模型では、原子の熱による格子振動を箱の中のフォノンとして扱う。一方、先に発表されていたアインシュタイン模型では、固体を相互作用のない量子的な調和振動子の集まりとして取り扱う。
デバイ模型は低温における比熱が温度の三乗 T3 に比例することを正しく予言する。また、アインシュタイン模型同様、比熱の高温におけるデュロン=プティの法則に従う振る舞いも正しく説明することができる。しかし、格子振動を単純化して扱っているため、中間的な温度における正確性には弱点がある。
デバイ模型についての厳密な取り扱いについては、Shubin & Sunada 2006を参照。
導出[編集]
デバイ模型はプランクの法則に対応する固体状態の模型である。プランクの法則では電磁波を箱の中のフォトンの気体として取り扱う。デバイ模型では格子振動を箱の中のフォノンとして取り扱う(箱とはその固体である)。計算の大半の過程はプランクの法則における計算と非常に似通っている。
一辺の長さが L の立方体を考える。井戸型ポテンシャルの項目より、箱内部の音の散乱の反響モード(ここでは1次元について考える)は以下で与えられる波長をもつ。
ここで n は整数である。フォノンのエネルギーは
である。ここで h はプランク定数であり、 νn はフォノンの周波数である。周波数は波長に反比例するという近似をすると、以下の式を得る。
cs は固体中の音速である。3次元では以下の式となる。
周波数は波長に反比例する(すなわち音速が一定である)という近似は低エネルギーのフォノンには良い近似であるが、高エネルギーではあまりうまくいかない(フォノンの項目を参照)。これはデバイ模型の限界のひとつであり、(高温や低温では正確な結果を出すのに対し)中間的な温度では結果が不正確になってしまっている。
箱の中の全エネルギーを計算しよう。
ここで N(En) は箱の中で En のエネルギーをもったフォノンの数である。言い換えると、全エネルギーはあるエネルギーにそのエネルギーをもつフォノンの数をかけ、総和をとったものに等しい(ここでは1次元を考えている)。3次元では、以下を得る。
ここでデバイ模型とプランクの法則に違いが生じる。箱の中の電磁波とは違い、フォノンの周波数は無限大になることができないためにフォノンのエネルギー状態が有限となる。フォノンの周波数は伝播の媒体(=固体の原子格子)に拘束される。横波のフォノンの図を以下で考える。
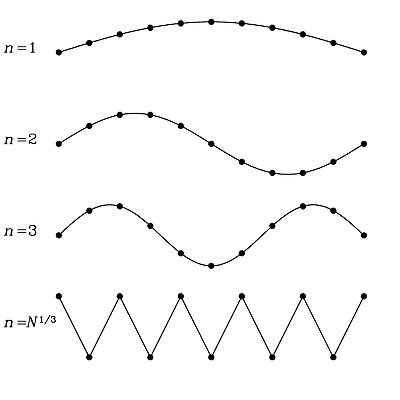
上の図で示すように、フォノンの波長の最小値が原子間隔の2倍であると仮定することは道理にかなっている。固体中には原子が N 個あり、今考えている固体は立方体であるから、一辺あたりの原子の数は 3√N 個である。よって原子間隔は L/3√N で与えられ、よって波長の最小値は
となり、さらにモード数 n の最大値は(フォトンでは無限大なのに対し)以下である。
この最大のモード数 nmax は3つのエネルギーの総和の上限である。
ゆっくりと振舞う正常な関数では、総和は積分で置き換えることができる。(このことはトーマス=フェルミ近似として知られている。)
ここまでの計算で、 N(E) (=エネルギー E をもつフォノンの数)には言及しなかった。フォノンはボース=アインシュタイン統計に従う。その分布は有名な以下のボース=アインシュタインの公式で与えられる。
フォノンは3つ(1つの縦波と(フォノンのエネルギーにほとんど影響しない)2つの横波)の偏光状態をとることができる。そのため上の公式を3倍する必要があり、ここでの分布は以下となる。
(実際には、「有効音速」cs := ceff を使うこともある。例えば、デバイ温度 TD(以下を参照)は単純にいうと ceff に比例し、より正確には縦波と横波の速度を区別(それぞれ1/3と2/3の寄与)してと表される。デバイ温度や有効音速は結晶の硬度の評価基準となっている。)
エネルギーを求める積分の式に N(E) を代入して以下を得る。
フォトンではこれらの積分は簡単に行うことができる。それは光の周波数が(少なくとも準古典的には)拘束されないためである。上の図が示すように、フォノンにおいてこれは正しくない。そこでデバイは3重積分を計算するため、球座標
を用いて、立方体を球の1/8と大胆に近似した。
ここで R は球の半径(立方体と球の1/8とで粒子数が一致するように定める)であり、 立方体の体積は単位格子の N 個分の体積である。
よって次を得る。
以上で正しい本来の積分を球の積分に置き換えたことにより、再び模型に不正確さが生じてしまっている。
エネルギーを求める積分は以下の式となる。
積分変数をに変えて
式を簡単に表記するため、デバイ温度 TD(定数をいくつかまとめたものであり、物質に依って異なる定数)を定義する。
以上より、比内部エネルギーを得ることができた。
ここで D3(x) は3次のデバイ関数である。
T に関して微分をすると、無次元量の熱容量を得る。これがデバイの比熱式である。
これらの公式はデバイ模型を任意の温度で扱っている。以下で導くより単純な公式は、高温や低温の極限における漸近的な振る舞いを記述する。既に言及したように、この低温や高温における振る舞いは(中間的な温度における振る舞いが不正確なのに対して)正確である。低温でデバイ模型が正確なのは、デバイ模型は低周波数の正しい分散関係 E(ν) を与えるためである。また、高温で正確なのは周波数の間隔あたりの振動の数が正確な総和則に一致するためである。
デバイによる導出[編集]
実際には、デバイは上記の式を違ったやり方で、より単純に導いた。デバイは連続媒体の固体力学を用いて、ある値よりも小さい周波数の振動状態の数は
へと漸近することに気づいた。ここで V は体積であり、 F は弾性率と密度からデバイが計算した因子である。これらを温度 T の調和振動子で期待されるエネルギーと結びつけ(アインシュタインがアインシュタイン模型ついても用いた手法である)、以下エネルギーを得る。
振動周波数の上限が無限まで伸びているなら、この形式は低温で正しい T4 的な振る舞いを与える。しかしデバイは N 個の原子では 3N 個以上の振動状態はありえないと確信した。そして原子固体において、振動状態の周波数スペクトルの最大値は νm であり、全状態の数は 3N だと仮定した。
デバイはこの仮定が本当は正しくないことを知っていた(高周波数は仮定よりも間隔が狭い)。しかし一方で高温においてはデュロン=プティの法則に一致し、正しい振る舞いをする。この仮定によりエネルギーは以下で与えられる。
ここで TD は hνm/k である。
ここで D3 は後に3次のデバイ関数と名づけられた。
低温の極限[編集]
デバイ模型においては、のときデバイ固体の温度が「低い」とよぶ。このときの比熱は
であるが、この定積分の値は正確に求めることができ、以下となる。
低温の極限では、前述のデバイ模型の限界は適用されず、フォノンの熱容量と温度、弾性係数、原子あたりの体積の正確な関係を導くことができる(弾性係数や原子あたりの体積はデバイ温度に含まれている)。
高温の極限[編集]
デバイ模型においては、のときデバイ固体の温度が「高い」とよぶ。のとき、と近似することができ、以下が導かれる。
これはデュロン=プティの法則であり、比熱を上昇させてしまう非調和性を考慮にいれなくても非常に正確な結果が導かれる。導体や半導体の固体の全比熱においては、無視できない電子比熱の寄与がある。
デバイvs.アインシュタイン[編集]

温度の関数として予言される熱容量のグラフ
デバイ模型とアインシュタイン模型はどの程度実験値と一致するのであろうか?どちらも驚くほど近い結果を示すが、特に低温ではアインシュタイン模型よりもデバイ模型がよい一致を示すことが知られている。
2つの模型はどのように違うのだろうか?質問に答えるには、同じグラフに2つの結果を描くのがよいだろう。アインシュタイン模型もデバイ模型も熱容量の「関数形式」を導く。両方とも数学「模型」であり、スケールのない数学模型はありえない。スケールにより、数学模型は実世界での対応するものと結びついている。アインシュタイン模型の比熱は以下の式で与えられ、
そのスケールは ε / k である。一方、デバイ模型のスケールはデバイ温度 TD である。両方のスケールは、模型を実験データにあてはめることで得られる。(デバイ温度は理論的には音速と結晶の次元から計算される。)双方の手法は固体の比熱に違った方向や違った形でアプローチしているため、アインシュタインとデバイのスケールは異なる。すなわち
であり、よってこれらをそのまま同じグラフへと描くことは意味がない。同じものを取り扱っている模型ではあるが、スケールが異なるのである。そこでアインシュタイン温度を
と定義することもできるが、当然
である。そこで二つの温度の間の比
を探しだす必要がある。
アインシュタイン固体は単一の周波数 ε = ћω = hν をもつ量子調和振動子で構成されている。この周波数が実際に存在するとすれば、固体中の音速と関連しているはずである。固体中の音の伝播が、互いに衝突している原子の連続であると想像するならば、明らかに振動の周波数は原子格子が維持する最小の周波数 λmin と一致するはずである。
これはアインシュタイン温度をつくり
よって求めたい2つの温度の比は以下のようになる。
これにより、両方のモデルを同じグラフへと描くことができるようになった。付け加えると、この比は3次元球の8分円の体積 1/84/3πR3 とそれを含む立方体の体積 R3 の比の3乗根である。これはちょうど、エネルギー積分を近似する際にデバイによって用いられた補正因子でもある。
デバイ温度の表[編集]
デバイ模型は完全には正確ではないものの、(伝導電子などの他の比熱への寄与が無視できる)絶縁体や結晶性固体における低温の比熱ではよい近似となっている。金属の低温の比熱では、デバイ模型による格子比熱の T3 に比例する比熱への寄与に加え、電子の比熱への T に比例する寄与が無視できない(十分低温では電子による比熱の方が支配的になる)。この場合、デバイ模型とは別に自由電子の比熱を見積もる必要がある。以下の表はいくつかの物質におけるデバイ温度のリストである[2]。
| アルミニウム | 428 K |
| カドミウム | 209 K |
| クロム | 630 K |
| 銅 | 343.5 K |
| 金 | 165 K |
| 鉄 | 470 K |
| 鉛 | 105 K |
| マンガン | 410 K |
| ニッケル | 450 K |
| 白金 | 240 K |
| ケイ素 | 645 K |
| 銀 | 225 K |
| タンタル | 240 K |
| 錫(白色) | 200 K |
| チタン | 420 K |
| タングステン | 400 K |
| 亜鉛 | 327 K |
| 炭素 | 2230 K |
| 氷 | 192 K |
他の準粒子への拡張[編集]
フォノン(量子化された音波)の代わりに他のボース粒子である準粒子(例えば強磁性のマグノン(量子化されたスピン波))についてもデバイ模型を適用すると、容易に類似した結果を導くことができる。この場合、低周波数の準粒子は分散関係が異なる。(例えばフォノンのE(ν) ∝ k(但しk = 2π / λ)の代わりにマグノンでは E(ν) ∝ k2 となる。)また、総和則(例えば)も異なる。結果として、強磁性では熱容量へのマグノンの寄与()を求めることができる。この寄与は十分に低温ではフォノンの寄与()よりも支配的になる。一方金属では、低温での熱容量への主な寄与は電子による ∝ T の項である。電子はフェルミ粒子であるため、その比熱はアーノルド・ゾンマーフェルトに遡る別の手法によって計算しなければならない。
関連項目[編集]
出典[編集]
- ^ Debye, Peter (1912). “Zur Theorie der spezifischen Wärmen” (German). Annalen der Physik (Leipzig) 344 (14): 789–839. doi:10.1002/andp.19123441404.
- ^ Kittel, Charles, Introduction to Solid State Physics, 7th Ed., Wiley, (1996)(氷の項目を除く)
参考文献[編集]
- Shubin, Mikhail; Sunada, Toshikazu (2006). “Geometric Theory of Lattice Vibrations and Specific Heat”. Pure and Appl. Math. Quaterly 2 (3): 745-777. arXiv:math-ph/0512088. doi:10.4310/PAMQ.2006.v2.n3.a7. MRMR2252116.
- CRC Handbook of Chemistry and Physics, 56th Edition (1975-1976)
- Schroeder, Daniel V. An Introduction to Thermal Physics. Addison-Wesley, San Francisco, Calif. (2000). Section 7.5.
- Kittel, Charles, Introduction to Solid State Physics, 7th Ed., Wiley, (1996)







![{\displaystyle \lambda _{\rm {min}}={2L \over {\sqrt[{3}]{N}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dff19d64e6c52aa5bf6260645c7140e88d41258)
![{\displaystyle n_{\rm {max}}={\sqrt[{3}]{N}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/774f19c328fa29631d0760b2a8c577294a46bd1c)
![{\displaystyle U=\sum _{n_{x}}^{\sqrt[{3}]{N}}\sum _{n_{y}}^{\sqrt[{3}]{N}}\sum _{n_{z}}^{\sqrt[{3}]{N}}E_{n}\,{\bar {N}}(E_{n})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6758e94a5462fd215c298ebb8d07b7c7e62faa0)
![{\displaystyle U\approx \int _{0}^{\sqrt[{3}]{N}}\int _{0}^{\sqrt[{3}]{N}}\int _{0}^{\sqrt[{3}]{N}}E(n)\,{\bar {N}}\left(E(n)\right)\,dn_{x}\,dn_{y}\,dn_{z}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90594627f2f33b29dbee96e79f62e8e3b9f86315)



![{\displaystyle U=\int _{0}^{\sqrt[{3}]{N}}\int _{0}^{\sqrt[{3}]{N}}\int _{0}^{\sqrt[{3}]{N}}E(n)\,{3 \over e^{E(n)/kT}-1}\,dn_{x}\,dn_{y}\,dn_{z}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60c36e0460a0819073e25fdf9c29389ab717630d)



![{\displaystyle R={\sqrt[{3}]{6N \over \pi }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10c56ad20622c9fb0fd910654309d0de1b975a93)



![{\displaystyle T_{D}\ {\stackrel {\mathrm {def} }{=}}\ {hc_{s}R \over 2Lk}={hc_{s} \over 2Lk}{\sqrt[{3}]{6N \over \pi }}={hc_{s} \over 2k}{\sqrt[{3}]{{6 \over \pi }{N \over V}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/411d5aa9ab5603b7ea4354a1a15d081145b5d11d)






















![{\displaystyle \nu ={c_{s} \over \lambda }={c_{s}{\sqrt[{3}]{N}} \over 2L}={c_{s} \over 2}{\sqrt[{3}]{N \over V}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d536a428a6732711cef27c5c9d7595d3db721b6)
![{\displaystyle T_{E}={\epsilon \over k}={h\nu \over k}={hc_{s} \over 2k}{\sqrt[{3}]{N \over V}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/deac1d0864c1435919b96e71a86aad5e5c61426c)
![{\displaystyle {T_{E} \over T_{D}}={\sqrt[{3}]{\pi \over 6}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73e4953d96f5e1cc8647c33643dbf65ae493cc34)


