「0.999...」の版間の差分
0.999...が1に等しいことの証明へのリダイレクト |
en:0.999... 16:56, 5 January 2007 の版より翻訳。著者:BradBeattie, Mets501, Melchoir, Noe, The Anome, Calbaer et al. |
||
| 1行目: | 1行目: | ||
<!-- NOTE: The content of this article is well-established. If you have an argument against one or more of the proofs listed here, please read the FAQ on [[Talk:0.999...]], or discuss it on [[Talk:0.999.../Arguments]]. However, please understand that the earlier, more naive proofs are not as rigorous as the later ones as they intend to appeal to intuition, and as such may require further justification to be complete. Thank you. --> |
|||
#REDIRECT [[0.999...が1に等しいことの証明]] |
|||
[[Image:999 Perspective.png|300px|right]]<!--[[Image:999 Perspective-color.png|300px|right]]--> |
|||
[[数学]]においては、 [[循環小数]]で '''0.999...''' と書かれる[[実数]]は [[1]] と ''完全に'' [[等式|等しい]]("0.999..." は <math>0.\dot{9}</math> または <math>0.\bar{9}</math> などとも書かれる) 。 換言すれば、 "0.999..." は "1" という記号と同じ数を表している。この等式に関するさまざまな [[証明]]が、厳密性、望ましいと思われる実数の研究結果、前提条件や歴史的背景、さらには対象となる読者、というそれぞれの多様性に応じて練り上げられてきた。 |
|||
この等式は長い間教科書において指導されてきており、ここ数十年間、[[数学教育学|数学教育]]の学者によりこの等式に対する生徒の反応が研究されているが、生徒はしばしばこの等式を受け入れない。生徒たちの推論は、概して実数に関するいくつかの共通の誤った直観に基づいている。それは、例えば、一つ一つの[[除法|小数展開]]がただ一つの数に対応するに違いないという考えであったり、[[無限小]]という量が存在するという期待であったり、[[算数]]が崩壊するという予想であったり、[[極限]]が理解する能力の欠如であったりする。もしくは、単に 0.999… には "最後の 9" があると考えているだけかもしれない。これらの考えは、実数に関しては正しくないが、これは[[有理数]]から実数を系統立てて構成することにより証明可能であり、また、そのような構成方法から 0.999...= 1 であることを直接証明することができる。同時に、直観によって想像される現象のいくつかは他の数体系においても起こりうる。さらに、"0.999..." と書ける対象が厳密に 1 [[不等式|より小さく]]なる数体系すらある。 |
|||
1 という数が2つの小数展開をもつということは、十進法に限った特殊性ではない.同様の現象が 10 以外の[[整数]]を[[基数]]とする場合にも起こる。さらに、数学者たちは非整数を基数として1を書き表す方法が何通り考えられるかについても研究してきた。また、この現象は 1 という数に限ったことではない。すべての 0 でない有限小数は後に 9 が続く別表現をもっている。簡単のため通常は、有限小数で表す方が好まれるが、さらに言えばこのことが「有限小数が''たった一つの''表現方法である」という誤解を招く原因ともなりうる。実際、無限小数展開が許されると、すべての[[位取り記数法]]はあいまいな数たちを無数に含むことになる。このように1つの数がさまざまな方法で表されるということは、[[小数]]の十進展開のパターンや[[カントール集合]]とよばれる単純なフラクタルの構造をよりよく理解するために適用されてきた。また、それらは実数全体の集合の無限性に対する古典的な研究の際にも起こっている。 |
|||
==0.999... とは何か== |
|||
0.999... は[[十進法]]で書かれた数であり、これが 1 に等しいという最も単純な証明のいくつかは、この記数法の便利な[[四則演算|算術]]的性質に依存している。 |
|||
十進小数のほとんどの計算([[加法]],[[減法]],[[乗法]],[[除法]],[[不等式|比較]])が整数の場合と同じ "桁レベルの操作" により為されている。また、整数の場合と同様に、ある桁が異なる任意の2つの''有限''小数は(あとに 0 がずっと続く場合を無視して)異なる数を表す。特に、"0.999...9" と表される任意の数(9は有限個)は厳密に 1 より小さい。 |
|||
省略記号 "..." の意味は厳密に特定されなければならない。ここでの "..." の用法は、言語もしくは 0.999...9 における "..." の用法とは異なる。後者の用法は、''有限''な部分を明言しなかったり省略したりする用法である。[[循環小数]]に対して用いるときには、"..." はある''無限''な部分を明言しないことを意味する。特に、0.999... は[[数列]] {0.9, 0.99, 0.999, 0.9999, ...} の[[極限]](これは、''k''= 1, 2, 3, ..., ∞ に対し 9 × 0.1<sup>''k''</sup> の形をしたすべての項の和に等しい)を表している。0.999... の誤った解釈は、これが 1 に等しいことに関する誤解の原因となる。 |
|||
等式 0.999...=1 の証明はいろいろある。これを代数的に示す前に、『2つの[[実数]]が等しいのは、これらの差(の絶対値)が(第3の)正の実数に等しくない場合に限る』ことに注意する。1 と 0.999... との距離は、任意に与えられた任意の正の数より小さい(これは上記の数列で定義される[[閉区間]]と[[三角不等式]]を用いて形式的に証明できる)。したがって、この距離は 0 であり、1 と 0.999... は等しい。このことを用いると |
|||
例えば 0.333... = <sup>1</sup>/<sub>3</sub> である理由も説明することができる。 |
|||
整数や有限小数の場合と異なり、それ以外の表記法は1つの数をいくつかの方法で表すことができる。例えば、[[分数]]を用いると、 |
|||
<sup>1</sup>/<sub>3</sub> = <sup>2</sup>/<sub>6</sub> となる。 |
|||
しかしながら、無限小数は1つの数を高々2つの方法でしか表すことができない。もし、2つの方法があったとすると、そのうちの1つは最後に 9 が無限に続く形であり、もう1つは有限で終わる形である(すなわち、あるところから先は 0 が繰り返す列からなる)。 |
|||
==桁ごとの操作== |
|||
=== 分数を用いた証明 === |
|||
無限小数が有限小数の必然的な拡張である1つの理由は、分数を表現することである。[[筆算]]を用いると <sup>1</sup>/<sub>3</sub> のような、整数の単純な割り算が循環小数 0.333... となる。ここで 3 は終わることなく永遠に続く。 |
|||
この小数を用いて、0.999...=1 を即座に証明することができる。3と3の積は各桁に 9 を生ずるので、 |
|||
3 × 0.333… は 0.999 に等しい.一方、<sup>1</sup>/<sub>3</sub> は 1 である。したがって 0.999...=1 である。<ref name="CME">cf. 同様な議論の二進数版も以下にある。 Silvanus P. Thompson, ''Calculus made easy'', St. Martin's Press, New York, 1998. ISBN 0-312-18548-0.</ref> この証明の別の形として、<sup>1</sup>/<sub>9</sub> = 0.111… に 9 を掛けることもできる。 |
|||
<math> |
|||
\begin{align} |
|||
0.333\dots &= \frac{1}{3} \\ |
|||
3 \times 0.333\dots &= 3 \times \frac{1}{3} = \frac{3 \times 1}{3} \\ |
|||
0.999\dots &= 1 |
|||
\end{align} |
|||
</math> |
|||
=== 代数的な証明 === |
|||
もう一つの証明はもっと簡潔に他の循環小数にも適用できる。十進法で表現された数に 10 を掛けると、数字は変化することなく、小数点が1つ右に移動する。ゆえに 10 × 0.999… は 9.999… に等しく、これはもとの数に比べて 9 大きい。このことを見るために、0.999... を 9.999... から引くときに、引き算が桁ごとに扱えるとみなすと、小数点以下各桁において、その結果は 9−9 すなわち 0 である。ところが、小数点のあとに永遠に続く 0 は数を変化させないので、この差はまさしく 9 である。最後の段階では代数を用いる。問題の小数 0.999... を ''c'' と呼ぶ。すると、 |
|||
10''c'' − ''c'' = 9 であり、これは 9''c'' = 9 と同値である。両辺を 9 で割ることにより、''c''=1 が得られ、証明が完了する。 |
|||
<ref name="CME"/> 数式を用いて書くと以下のようになる。 |
|||
<math> |
|||
\begin{align} |
|||
c &= 0.999\ldots \\ |
|||
10 c &= 9.999\ldots \\ |
|||
10 c - c &= 9.999\ldots - 0.999\ldots \\ |
|||
9 c &= 9 \\ |
|||
c &= 1 |
|||
\end{align} |
|||
</math> |
|||
以上2つの証明における桁ごとの操作の正当性は、鵜呑みにしたり、自明の理と見なしたりする必要はない。このことは "小数"と "小数が表す数" の間の基本的な関係を調べることによって証明することができる。 |
|||
有限小数に関しては、この過程は実数の計算法則にのみ依存している。 |
|||
この操作が無限小数にも適用できることを証明するためには、[[実解析]]の手法を必要とする。 |
|||
== 実解析 == |
|||
0.999... の問題は数学の形式的な発展には影響を与えないので、これは[[実解析]]の基本的な定理や命題が証明されるまで後回しにすることができる。1つの要請は十進法で表現される実数を特徴づけることである。これは、『符号、整数部分を形成する任意個数の数字の有限列、小数点、そして小数部分を形成する数字の列』から構成される。 |
|||
0.999... を議論する目的においては、整数部分は ''b''<sub>0</sub> とまとめうる。また、負の数は考えなくてよいので、小数展開は |
|||
:<math>b_0.b_1b_2b_3b_4b_5\dots</math> |
|||
の形である。整数部分と違って、小数部分は有限の桁数に制限されないことが肝心である。これは [[位取り記数法]]であるから、500 における "5" は 50 における "5" の10倍の大きさに寄与する。また、0.05 における "5" は 0.5 における "5" の 1/10 倍の大きさに寄与する。 |
|||
===無限数列と無限級数=== |
|||
おそらく、小数展開の最も一般的な成果は、小数展開を[[無限数列]]の和として定義することである。一般的には |
|||
:<math>b_0 . b_1 b_2 b_3 b_4 \ldots = b_0 + b_1({\tfrac{1}{10}}) + b_2({\tfrac{1}{10}})^2 + b_3({\tfrac{1}{10}})^3 + b_4({\tfrac{1}{10}})^4 + \cdots </math> |
|||
と表される。 |
|||
0.999... に対しては[[総和|無限等比級数]]に関する有力な[[収束]]定理 |
|||
<ref>Rudin p.61, Theorem 3.26; J. Stewart p.706</ref> |
|||
: <math>|r| < 1\quad</math> ならば <math>\quad ar+ar^2+ar^3+\cdots = \frac{ar}{1-r}</math> |
|||
を適用することが可能である。 |
|||
0.999... はこの和において公比を <math>r=\textstyle\frac{1}{10}</math> としたものであるから、この定理により |
|||
:<math>0.999\ldots = 9(\tfrac{1}{10}) + 9({\tfrac{1}{10}})^2 + 9({\tfrac{1}{10}})^3 + \cdots = \frac{9({\tfrac{1}{10}})}{1-{\tfrac{1}{10}}} = 1</math> |
|||
と簡単に問題を解決することができる。この(実際には 10=9.999... の)証明は早くも 1770 年の[[レオンハルト・オイラー]]による''[[Elements of Algebra]]''<ref>Euler p.170</ref> において見られる。 |
|||
[[Image:base4 333.svg|left|thumb|200px|Limits: The unit interval, including the '''base-4''' decimal sequence (.3, .33, .333, …) converging to 1.]] |
|||
等比数列の和の公式それ自身はオイラー以前の成果である。代表的な18世紀の導出法においては上記の[[#代数的な証明|証明]]と同じような項ごとの操作を用いていた。1811年になってやっと、Bonnycastle の教科書 ''An Introduction to Algebra'' では等比級数に関するこのような議論が 0.999... と同様の「巧妙な操作」を正当化するために用いられている。<ref>Grattan-Guinness p.69; Bonnycastle p.177</ref> |
|||
このような寛大な求和法に対抗した19世紀の反動により「無限数列の和はその部分和の極限として定義される」という、現在においても支配的な定義が生み出された。この定理に相当する証明ではこの数列を系統だてて計算しており、それは証明に基づいた微積分学や解析学の入門書に見られる。<ref>例えば、 J. Stewart p.706, Rudin p.61, Protter and Morrey p.213, Pugh p.180, J.B. Conway p.31</ref> |
|||
数列 {''x''<sub>0</sub>, ''x''<sub>1</sub>, ''x''<sub>2</sub>, …} は ''n'' が増加するにしたがって距離 | ''x'' − ''x''<sub>''n''</sub> | が 0 に近づくとき[[極限]] ''x'' をもつ。 |
|||
等式 0.999...=1 自身は以下のように極限として表すことにより証明される。 |
|||
:<math>0.999\ldots = \lim_{n\to\infty}0.\underbrace{ 99\ldots9 }_{n} = \lim_{n\to\infty}\sum_{k = 1}^n\frac{9}{10^k} = \lim_{n\to\infty}\left(1-\frac{1}{10^n}\right) = 1-\lim_{n\to\infty}\frac{1}{10^n} = 1.\,</math><ref>この極限については例えば以下に従う:from Rudin p. 57, Theorem 3.20e。 より直接的なアプローチについては、以下も参照: Finney, Weir, Giordano (2001) ''Thomas' Calculus: Early Transcendentals'' 10ed, Addison-Wesley, New York. Section 8.1, example 2(a), example 6(b).</ref> |
|||
最後のステップ ( lim <sup>1</sup>/<sub>10<sup>''n''</sup></sub> = 0 ) は、実数が [[アルキメデス性]] (Archimedean property) をもつという公理を用いて説明される。また、極限に基づく 0.999... に対するこの姿勢は、幾分わかりやすいがいくらか不正確な言葉を用いて説明されることがある。例えば、1846年の教科書 ''The University Arithmetic'' は「0.999...と無限に続く数は1である。なぜなら 9 を積み重ねるたびにその値は 1 に近づくからである」と説明しており、1895年の ''Arithmetic for Schools'' は「9 を十分多く用いれば、1 と 0.999... の距離は驚くほど小さい値である」と説明している。<ref>Davies p.175; Smith and Harrington p.115</ref> |
|||
このような発見的指導法においては、生徒に「0.999...それ自身は 1 より小さい」という印象をもたせがちである。詳しくは [[#教育における懐疑主義|後述]]。 |
|||
===区間縮小法と上限=== |
|||
[[Image:999 Intervals C.svg|right|thumb|Nested intervals: in base 3, 1 = 1.000… = 0.222…]] |
|||
前述の級数による定義は小数展開によって実数を定義する簡単な方法である。もう一つのアプローチは逆の手順をたどるものである。すなわち、先に実数を与え、その実数を表す小数展開を定義する方法である。 |
|||
実数 ''x'' が [[閉区間]] [0, 10] (すなわち 0 以上 10 以下)に属することが知られているとする。ここでこの区間を、端点のみで重なる 10 個の区間 [0, 1], [1, 2], [2, 3], ... , [9, 10] に分割する。実数 ''x'' はこのうちの少なくとも1つの区間に属する。例えば、それが区間 [2, 3] に属するときには、数字 "2" を記録することにする。さらにこれを [2, 2.1], [2.1, 2.2], …, [2.8, 2.9], [2.9, 3] なる区間に分割する。この操作を繰り返すと ''b''<sub>0</sub>, ''b''<sub>1</sub>, ''b''<sub>2</sub>, ''b''<sub>3</sub>, … という無限数列により名づけられた[[縮小区間]]が生じ、 |
|||
:''x'' = ''b''<sub>0</sub>.''b''<sub>1</sub>''b''<sub>2</sub>''b''<sub>3</sub>… |
|||
と記録される。 |
|||
この表現形式に従えば、実数 1 は区間 [0, 1] と区間 [1, 2] のいずれにも属し、数字を選ぶときにどちらの区間を選ぶこともできるので、1=1.000... と 1=0.999... の2通りの表現が得られることになる。この表現形式が記号 "=" の濫用でないことを保証するためには、それぞれの小数に対し唯一の実数を構成しなおす方法が必要になる。このことは極限を用いてなされるが、順序の議論を続ける別の構成方法もある。<ref>Beals p.22; I. Stewart p.34</ref> |
|||
[[区間縮小法の原理]]を用いるのが率直な方法である。この原理によれば、閉区間の無限減少列が与えられ、その幅が 0 に収束するとき、それらの区間の[[積集合|共通部分]]がただ1つの実数であることが保証される。したがって |
|||
''b''<sub>0</sub>.''b''<sub>1</sub>''b''<sub>2</sub>''b''<sub>3</sub>… |
|||
はすべての区間 [''b''<sub>0</sub>, ''b''<sub>0</sub> + 1], [''b''<sub>0</sub>.''b''<sub>1</sub>, ''b''<sub>0</sub>.''b''<sub>1</sub> + 0.1], ... に属する唯一の実数であると定義される。したがって 0.999... は [0, 1], [0.9, 1], [0.99, 1], ... , [0.99…9, 1] と、任意個の 9 を含むすべての区間に属する唯一の実数である。一方、実数 1 はこれら1つ1つの区間に属するので 0.999… = 1 となる。<ref>Bartle and Sherbert pp.60-62; Pedrick p.29; Sohrab p.46</ref> |
|||
『区間縮小法の原理』は通常、実数に関するもっと基本的な特徴である [[上界]] (least upper bound, ''suprema'') の存在に基づいている。 |
|||
これらの事実を直接的に用いると、''b''<sub>0</sub>.''b''<sub>1</sub>''b''<sub>2</sub>''b''<sub>3</sub>... を |
|||
近似値の集合{''b''<sub>0</sub>, ''b''<sub>0</sub>.''b''<sub>1</sub>, ''b''<sub>0</sub>.''b''<sub>1</sub>''b''<sub>2</sub>, ...} の上界として定義することができる。<ref>Apostol pp.9, 11-12; Beals p.22; Rosenlicht p.27</ref> |
|||
この定義(または区間縮小法による定義)は区間分割の手続きと矛盾がないことが示せるので再び 0.999...=1 を得る。 |
|||
[[トム・アポストル]]は次のように結論した。 |
|||
:「実数が2つの異なる小数表示をもつ可能性があるという事実は、単に、実数を[[集合|元]]にもつ異なる2つの集合が等しい上界をもつ可能性があるという事実の裏返しに過ぎない。」<ref>Apostol p.12</ref> |
|||
== 教育における懐疑主義 == |
|||
数学を学ぶ生徒は 0.999... と 1 が等しいことをしばしば受け入れない。その理由は彼らの本質的に異なる状況から [[極限]]の概念に対する深い懐疑心、そして[[無限小]]の性質の拒絶まで多岐にわたる。この困惑に寄与する多くの共通な要因がある。 |
|||
* 生徒はしばしば、「一つの数はただ1つの小数で表すことができるという信念に精神的に縛られている」。明白に異なる2つの小数が同じ数を表すことを知ると、それは[[パラドックス|逆説]]であるように見える。見かけ上よく知られた数 1 の登場がその感情をさらに強める。<ref>Bunch p.119; Tall and Schwarzenberger p.6. 最後の提案は Burrell (p.28) による。すなわち、「おそらくすべての数の中で最も安心する数は 1 であろう。したがって、0.999... を 1 として扱うときにとりわけ不安を覚える。」</ref> |
|||
* "0.999..." (または同様の表現)を、多いけれども有限の個数の "9" の列(おそらく可変であり特定できない長さ)として解釈する生徒もいる。たとえ生徒が "9" の無限個の列であることを受け入れたとしても、まだ最後の "9" が「無限の彼方に」あると期待しているかもしれない。<ref>Tall and Schwarzenberger pp.6-7; Tall 2000 p.221</ref> |
|||
* 直観的であいまいな指導により、生徒は数列の極限を、一つの決まった値ではなくある種の無限操作と考えるようになる。それは数列の各項はその極限に達する必要はないからである。生徒が数列とその極限の違いを受け入れても、彼らは "0.999..." を極限ではなく数列を意味するものと読む可能性がある。<ref>Tall and Schwarzenberger p.6; Tall 2000 p.221</ref> |
|||
* 0.999... を 1 よりもごく僅かだけ小さい、固定された値であるとみなす生徒もいる。 |
|||
* [[極限|収束列]]の値を実際の値ではなく近似値であると信じている生徒もいる。 |
|||
これらの考えは、通常の実数を扱う文脈においては誤っている。しかしながら、一般的な数学的道具として発明された、もしくは、0.999... を理解するのに有益な[[反例]]としての、より精巧な構造においてはそれらの考えの多くが部分的に正しいことが示される。 |
|||
このような説明の多くはデビット・トール (David Tall) 教授により発見された。教授は、自らが遭遇した大学生の誤解のいくつかについて、それを生徒に抱かせる原因となった指導法と認識の特徴を研究している。非常に多くの生徒がなぜ最初はこの等式を受け入れないのかを調べるために生徒を面接して、次のようなことを発見した。「生徒は 0.999... を、決まった値ではなく 1 に限りなく近づく数の列として理解し続けようとする。その原因は『先生は小数点以下の桁数がいくつあるかをはっきりと教えてなかった』という指導法の欠陥または『0.999... は 1 より小さい数の中で、存在しうる、1 に最も近い小数である』という認識である。」<ref>Tall 2000 p.221</ref> |
|||
基本的な証明の中で 0.333...=<sup>1</sup>/<sub>3</sub> の両辺を3倍する方法は、0.999...=1 であることを受け入れない生徒に有無を言わせないための、明らかに成功する戦略であるかのように見える。しかしながら、第1の等式を信じることと、第2の等式を信じないことの矛盾に直面すると、今度は第1の等式を疑い始める生徒もいるし、または単に不満を抱くだけの生徒もいる。<ref>Tall 1976 pp.10-14</ref> これより進んだ方法で簡単に分かるものもまたない。厳密な定義を十分適用する能力のある生徒が、0.999... を含めてさらに進んだ数学の結果に驚いたとしても、なお直観的な想像に頼ってしまうことがある。例えば、ある解析学を学ぶ生徒は 0.333...=<sup>1</sup>/<sub>3</sub> であることを [[上限]]の定義を用いて証明することができるが、その後もなお、昔の筆算の理解に基づいて 0.999...<1 であると主張した。<ref>Pinto and Tall p.5, Edwards and Ward pp.416-417</ref> 別の生徒は、<sup>1</sup>/<sub>3</sub>=0.333... であることを証明することができるが、[[#分数を用いた証明|分数を用いた証明]]に直面して「論理」が数学の計算を征服していると主張する。 |
|||
ジョセフ・メイザー (Joseph Mazur) は別の才能豊かな微積分学の生徒について語る。その生徒は「私が授業で言ったことにはほとんどすべて異議を唱えるが、自分の使っている計算機には決して異議を唱えない」。さらに、23 の平方根を計算することも含めて、数学をするのに必要なのは 9 桁(程度)だと信じるようになった。その生徒は 9.999...=10 であるという極限の議論に相変わらず不愉快な感じを抱いていたが、それは「乱暴な推測をする、無限概念の成長過程(wildly imagined infinite growing process)」と呼ばれる。<ref>Mazur pp.137-141</ref> |
|||
エド・デュビンスキー (Ed Dubinsky) による数学学習の理論 (APOS theory)の一部分として、デュビンスキーとその共同研究者 (2005) は、 0.999... を「1 から無限に小さい距離だけ離れている数を表す有限で不確定の文字列」であると思う生徒は「無限小数の構成過程の完全な概念がまだ形成されていない」と述べた。 |
|||
たとえ 0.999... の構成過程の完全な概念を身につけた生徒であっても、まだその過程を(既に持っている "1" の概念と同様の)一つの「対象」としてとらえ直すことができずに、0.999... という一つの過程と 1 という数の存在を矛盾するものととらえるかもしれない。デュビンスキーらはまた、「一つの対象としてとらえ直す」というこの精神的能力が、1/3 それ自体を数と見なしたり、自然数の集合それ自身を一つの対象として取り扱ったりすることと関係していると考える。<ref>Dubinsky 他 261-262</ref> |
|||
== 実数 == |
|||
他のアプローチでは、[[公理的集合論]]を用いて、有理数をもとにして構造が確かな[[実数#実数の様々な構成|実数を構成し]]、それを系統だてて定義する。[[自然数]] (0, 1, 2, ...) は 0 から始まり増加していく数であり、すべての数は『次の数 (successor)』を持っている。自然数にその −1 倍を付け加えて拡張することによってすべての [[整数]]が得られる。 さらに比に拡張し、[[有理数]]を得る。これらの数体系は、加法、減法、乗法、除法の算法を伴っている。さらに巧妙に、そこには[[距離]]が定義されており、ある数が別の数に比べて小さい、大きい、または等しいなどの判断ができる。 |
|||
有理数から実数への拡張が重要なステップである。このステップを達成するためには少なくとも2つの一般的な方法がある。ともに 1872年に発表された[[実数の切断]] (Dedekind cut) と[[コーシー列]] (Cauchy sequence) である。これらの構成法を直接的に用いて 0.999...=1 であることを証明している実解析の教科書は見られない。ここ数十年の傾向は、公理的に解析学を記述することである。実数の構成が提供されたときでさえ、それは実数の公理を証明するために用いられ、その上で公理的解析論による証明を支持している。しかしながら、著者の中には、実数の構成から始めることをもっと適切に、もっと論理的に行うことにより、証明すべき結果はもっと直接的になされる(self-contained)という考えを主張する人もいる。<ref>統合の歴史的な過程は以下を参照: Griffiths and Hilton (p.xiv) in 1970。 また、再び Pugh (p.10) in 2001。 両方とも実際には公理的解析論よりもデデキンド切断を好んでいる。切断の方法の教科書については以下を参照:Pugh p.17 or Rudin p.17. 論理的視点については Pugh p.10, Rudin p.ix, or Munkres p.30</ref> |
|||
=== 実数の切断 === |
|||
[[実数の切断]]のアプローチにおいては、それぞれの実数 ''x'' は、それより小さいすべての有理数からなる無限集合である。<ref> Enderton (p.113) は以下の記述を与えている。『デデキント切断の背景にあるアイディアは、有理数、つまり ''x'' より小さいすべての有理数の無限集合を与えられることによって実数 ''x'' が名づけられるということである。循環論法を避けるため、この方法で得られる有理数の集合が特徴づけられなければならない。』</ref> 特に、実数 1 は 1 より小さいすべての有理数の集合である。<ref>Rudin pp.17-20, Richman p.399, or Enderton p.119。正確には、この3人はこの切断をそれぞれ 1*, 1<sup>−</sup>, 1<sub>''R''</sub> と呼んでいる。3人ともそれを伝統的な 1 の定義と同一視している。Rudin と Enderton が『実数の切断』と呼ぶものを Richman は『nonprincipal な実数の切断』と呼ぶことに注意。 </ref> 実数の切断により、正の数の小数展開が簡単に決定できる。すなわち、小数展開表示を、ある段階の表示より小さい有理数の集合として定義するのである。したがって、実数 0.999... は ''r'' < 0, ''r'' < 0.9, ''r'' < 0.99, ... のどれかを満たす有理数 ''r'' の集合として定義する。一般的には、ある ''n'' に対して、 1 − (<sup>1</sup>/<sub>10</sub>)<sup>''n''</sup> の形の数より小さい有理数の集合として定義する。<ref>Richman p.399</ref> 0.999... のすべての元は 1 より小さいので、これは実数 1 の元である。逆に、実数 1 の元は 1 より小さい有理数 ''a''/''b'' であり、したがって ''a''/''b'' < 1 − (<sup>1</sup>/<sub>10</sub>)<sup>''b''</sup> となる。0.999... と 1 は全く同じ有理数を含むので、これらは同じ集合であり、0.999...=1 である。 |
|||
実数の切断による実数の定義は、最初 1872 年に[[リヒャルト・デーデキント]]によって発表された。<ref name="MacTutor2">{{cite web |url=http://www-gap.dcs.st-and.ac.uk/~history/PrintHT/Real_numbers_2.html |title=History topic: The real numbers: Stevin to Hilbert |author=J J O'Connor and E F Robertson |work=MacTutor History of Mathematics |date=October 2005 |accessdate=8月30日|accessyear=2006年}}</ref> 上記の、実数をそれぞれの小数展開に帰着させる方法は、フレッド・リッチマン (Fred Richman) の "Is 0.999...= 1?" という説明的な論文による。これは ''[[Mathematics Magazine]]'' に投稿されているが、これは数学を学ぶ学部生を対象としている。<ref>{{cite web |url=http://www.maa.org/pubs/mm-guide.html |title=Mathematics Magazine:Guidelines for Authors |publisher=The Mathematical Association of America |accessdate=8月23日|accessyear=2006年}}</ref> リッチマンは、有理数の任意の[[稠密]]な部分集合における切断を考えても同様な結果をもたらすことを注意している。特に彼は[[小数]]を用いたが、それにより証明はもっと直接的になる。「したがって、実数の伝統的な定義によれば、等式 0.9...=1 は最初から築かれている。」<ref>Richman pp.398-399</ref> Richman は、この手順をさらに修正して別の構造を導いており、それについて興味深く論じている。それについては以下の 「[[#他の数体系|「他の数体系」]]」 を参照。 |
|||
=== コーシー列 === |
|||
実数を構成するもう1つの方法は、有理数の順序をもっと間接的に用いることである。最初に,''x'' と ''y'' の距離は絶対値 | ''x'' − ''y'' | として定義できる。ここに、絶対値 | ''z'' | は ''z'' と −''z'' の小さくない方として定義されていて、したがって負にはならない。すると実数は、この距離を用いた[[コーシー列]]という有理数の列であると定義することができる。コーシー列とは、自然数から有理数への写像、数列 (''x''<sub>0</sub>, ''x''<sub>1</sub>, ''x''<sub>2</sub>, ...) において、任意の正の数 δ に対して、''N'' が存在し、以下の条件を満たす: ''N'' より大きいすべての ''m'', ''n'' に対して | ''x''<sub>''m''</sub> − ''x''<sub>''n''</sub>| ≤ δ が成り立つ(2項間の距離が次第に小さくなる)ものである。<ref>Griffiths & Hilton §24.2 "Sequences" p.386</ref> |
|||
数列 (''x''<sub>''n''</sub>) と (''y''<sub>''n''</sub>) が2つのコーシー列であるとき、(''x''<sub>''n''</sub> − ''y''<sub>''n''</sub>) が極限 0 をもつならば、これらのコーシー列は実数として等しいと定められる。小数 ''b''<sub>0</sub>.''b''<sub>1</sub>''b''<sub>2</sub>''b''<sub>3</sub>... を各桁で順に切捨てていくことにより、有理数からなるコーシー列が得られ、その真の値が定義される。<ref>Griffiths & Hilton pp.388, 393</ref> こうしてこの形式で、有理数の数列 |
|||
:<math>\left(1 - 0, 1 - {9 \over 10}, 1 - {99 \over 100}, \dots\right) |
|||
= \left(1, {1 \over 10}, {1 \over 100}, \dots \right)</math> |
|||
が極限 0 をもつことを示すことになる。したがって、''n''=0, 1, 2, ... に対してこの数列の第 ''n'' 項を考えると、 |
|||
:<math>\lim_{n\rightarrow\infty}\frac{1}{10^n} = 0</math> |
|||
であることを示さなければならない。 |
|||
最後の極限は簡単であり<ref>Griffiths & Hilton pp.395</ref>、例えば数列の[[極限]]の定義において、 ε = ''a''/''b'' > 0 に対し |
|||
''N'' = ''b'' をとることにより示される。したがって,再び 0.999...=1 を得る。 |
|||
コーシー列としての実数の定義については、最初に(いずれも)1872 年に [[エドゥアルト・ハイネ]] と [[ゲオルク・カントール]] により独立に発表された。<ref name="MacTutor2" /> 0.999...=1 の証明も含めて、小数展開による上記のアプローチは 1970 年に グリフィス (Griffiths) とヒルトン (Hilton) の書いた ''A comprehensive textbook of classical mathematics: A contemporary interpretation'' を厳密にたどっている。この本はよく知られた概念を現代の観点でもう一度見直してもらうために特定して書かれている。 <ref>Griffiths & Hilton pp.viii, 395</ref> |
|||
== 他の数体系 == |
|||
実数は非常に便利な数体系を形成しており、"0.999..." という表記法が実数を意味するものと考えることは根本的には『慣習』である。[[ウィリアム・ティモシー・ガワーズ]] (William Timothy Gowers) は ''Mathematics: A Very Short Introduction'' において、等式 0.999...=1 を結論することも同様に『慣習』であると述べている。すなわち、 |
|||
: 「しかしながら、それは決して独裁的な慣習ではない。なぜなら、それを受け入れなければ、一風変わった新しい対象を発明するか、または算数のよく知られた規則のいくつかを諦めるかのどちらかが強制されるからである。」<ref>Gowers p.60</ref> |
|||
新しい対象もしくは知られていない規則を用いて上の証明を再び解釈すると、0.999...≠1 であるような仮説の数体系に制限を加えることができる。リッチマンが述べたように、『ある人の証明は、別の人にとっては[[背理法]]である。(one man's proof is another man's ''reductio ad absurdum''.)』 <ref>Richman p.396; 彼の強調。この行は出版された論文の段落には見られるが、それより前に出されたプレプリントには見られない。 (訳注) ''reductio ad absurdum'' には「行き過ぎた議論」という意味もある。</ref> もし、 0.999... が 1 と異なれば、上の証明で立てられた少なくとも1つの仮定は潰れなければならない。 |
|||
===無限小=== |
|||
0.999...=1 のいくつかの証明は、通常の実数が[[アルキメデス的]]であること、すなわち、"0でない無限小は存在しない" ことに依存している。 |
|||
通常の実数に代わるいくつかのものを含むような、数学的に理路整然とした順序の導入された[[代数構造]]があるが、それは非アルキメデス的である。例えば、[[二元数]]は新しい無限小の要素 ε を含む。これは ε<sup>2</sup> = 0 であることを除けば [[複素数]] における虚数単位 ''i'' の類似である。結果として生じる構造は、記号処理系のための微分の理論 (automatic differentiation) で有用である。二元数には[[辞書式順序]]を与えることができ、この場合において ε の倍数は非アルキメデス的要素になる。<ref>Berz 439-442</ref> 実数に代わる構造を構成するもう一つの方法は、(特殊な例ではあるが)[[集合論]]や古典的な理論ではなく、[[トポス]]理論やそれに代わる諸論理を用いることである。例えば、『滑らかな無限小解析(smooth infinitesimal analysis)』 では[[逆元]]のない無限小が存在する。<ref>{{cite web|url=http://publish.uwo.ca/~jbell/invitation%20to%20SIA.pdf|title=An Invitation to Smooth Infinitesimal Analysis|author=John L. Bell |year=2003 |format=PDF |accessdate=6月29日 |accessyear=2006年}}</ref> |
|||
[[超準解析]]によってたくさんの無限小量(やその逆数)を含んだ体系が得られることはよく知られているが、これによって、普通とは異なり、しかもより直感的と思われる微積分へのアプローチが可能になる。<ref> 非標準的な数に関する完全な取り扱いは例えば以下を参照:Robinson's ''Non-standard Analysis''.</ref> 1972年にライトストーン (A.H. Lightstone) は超準解析に基づき、(0, 1) に属する超実数に対して一意的な "超小数展開" を対応させる考え方を展開した。ここで超小数展開とは超自然数で添字づけられた数字の列のことである。この枠組みにおいて、素朴には0.333... に対応する表示を2種類考えることができるが |
|||
::* 0.333...;...000... は正確には超小数と見なすことができないが |
|||
::* 0.333...;...333... はちょうど{{fraction|1|3}}と一致する |
|||
のでいずれにせよ0.333...と{{fraction|1|3}}の差は無限小ですらない。<ref>Lightstone pp.245-247。彼は表現の標準的な部分において、9 の繰返しの可能性を調べていない。</ref> |
|||
組合せ[[ゲーム理論]]も同様に、とくに関連のある一つの例として "無限二色ハッケンブッシュゲーム (infinite Blue-Red Hackenbush)" をもつ実数の代替構造を与える。1974年に、エルウィン・バールカンプ (Elwyn Berlekamp) は[[データ圧縮]]のアイディアに刺激されて ハッケンブッシュ文字列と実数の2進展開の関係について述べた。例えば、"ハッケンブッシュ文字列 (Hackenbush string)" LRRLRLRL... の値は 0.010101... = <sup>1</sup>/<sub>3</sub> である。しかしながら、文字列 LRLLL... (0.111...に対応する) の値は 1 に比べてごくわずかだけ小さい。 これらの2数(LRLLL... と 1)の差は [[超実数]] (surreal number) <sup>1</sup>/<sub>ω</sub> (ω は最初の [[無限序数]](infinite ordinal) ) である。これに関連するゲームは LRRRR… すなわち 0.000… である。<ref>Berlekamp, Conway, and Guy (pp.79-80, 307-311) は 1 と <sup>1</sup>/<sub>3</sub> について議論されており、さらに <sup>1</sup>/<sub>ω</sub> について触れられている。0.111... のゲームはバールカンプのルールに直接にしたがっており、それは以下に述べられている。{{cite web |url=http://www.maths.nott.ac.uk/personal/anw/Research/Hack/ |title=Hackenstrings and the 0.999… =1 FAQ |author=A. N. Walker |year=1999 |accessdate=6月29日|accessyear=2006年}}</ref> |
|||
===減法の崩壊=== |
|||
証明が崩されてしまうもう一つのパターンは単に 1 − 0.999… が存在しないのかどうか、という点である。なぜなら、減法は必ずしも可能でないからである。加法の演算をもつが、減法をもたない数学的構造は、[[可換]][[半群]]、可換[[モノイド]]、[[半環]] (semiring) を包括している。リッチマンは 0.999...<1 となるようにデザインされた、そのような2つの構造を考えた。 |
|||
まず、リッチマンは負でない ''decimal number'' を文字通り小数展開となるように定義する。彼は[[辞書式順序]]と加法を定義した。ここでは |
|||
0.999... < 1 であることに注意する。なぜなら単に、一の位において 0 < 1 となるからである。しかし、どんな「無限小数」 ''x'' に対しても 0.999... + ''x'' = 1 + ''x'' である。だから、decimal number に特徴的な一つのことは、加法が必ずしも打ち消しあわないということであり、もう一つは <sup>1</sup>/<sub>3</sub> に対応する decimal number は存在しないということである。乗法を定義すると、decimal number は正値全順序可換半環をなす。<ref>Richman pp.397-399</ref> |
|||
乗法を定義する際、リッチマンはまた、"cut ''D''" と呼ばれる別の構造を定義する。これは小数の切断の集合である。通常この定義は実数を導くが、彼は小数 ''d'' に対して、切断(−∞, ''d'' ) と "principal cut" (−∞, ''d'' ] の両方を許す。その結果、実数たちは小数と「不安定な状態で共存する(living uneasily together with)」ことになる。したがって、再び 0.999... < 1 を得る。"cut ''D''" には正の無限小は存在しないが、"一種の負の無限小" 0<sup>−</sup> が存在する。0<sup>−</sup> には小数展開は存在しない。彼は0.999... = 1 + 0<sup>−</sup> であると結論したが、一方、方程式 "0.999... + ''x'' = 1" は解をもたない。<ref>Richman pp.398-400. Rudin (p.23) は第1章の最後の練習問題として、この代替構造(ただし実数上)を選んでいる。</ref> |
|||
===''p''-進数=== |
|||
1 − 0.999... は何かと尋ねられると、生徒たちは数 "0.000...1" をしばしば発明する。これが意味を持つと持たないとにかかわらず、直観的な到達点は明らかである。すなわち、0.999... の "最後の 9" に 1 を足すことですべての 9 が 0 に変わって上の桁に送られ、一の位に 1 を残す、ということである。他の理由もあって、この考え方は正しくない。なぜなら 0.999... には "最後の9" がないからである。<ref>Gardiner p.98; Gowers p.60</ref> 『最後の9』を持つ無限な文字列を探すためには、どこか他のところを見なければならない。 |
|||
[[Image:4adic 333.svg|right|thumb|200px|The 4-adic integers (black points), including the sequence (3, 33, 333, …) converging to −1. The 10-adic analogue is ...999 = −1.]] |
|||
[[p進数|''p''-進数]]は[[整数論]]で興味がもたれている実数に代わる数体系である。実数と同様に、''p''-進数は[[コーシー列]]を経由して有理数から作ることができる。ただしこの構成には、0 は 1 よりも ''p'' に近く、''p<sup>n</sup>'' にはもっと近いという、普通と異なった距離を用いる。''p''-進数は素数 ''p'' に対しては体をなし、他の ''p'' (10 を含む)に対しては[[環 (数学)|環]]をなす。したがって,''p''-進数に計算を実行することができ、無限小は存在しない。 |
|||
『10-進数』は小数展開の類似であり、左の方へ進んでいく。10-進展開 ...999 はまさに "最後の 9" をもつが、"最初の9" はもたない。一の位に 1 を加えることができるが、すると 0 だけが残されて繰り上がりが続き、その結果 1 + ...999 = ...000 = 0 となる。すなわち、...999 = −1 である。<ref name="Fjelstad11">Fjelstad p.11</ref> もう一つの誘導の仕方は等比級数を用いる。"...999" の意味をもつ無限等比級数は実数においては収束しないが、10-進数では収束し、よく知られた公式を再び用いることができて |
|||
:<math>\ldots999 = 9 + 9(10) + 9(10)^2 + 9(10)^3 + \cdots = \frac{9}{1-10} = -1</math><ref>Fjelstad pp.14-15</ref> |
|||
となる。([[#無限数列と無限級数|前述の等比級数]]と比較せよ。)3番目の誘導方法はある中学1年生によって発明された。その生徒は教師が 0.999...=1 を極限を用いて行った議論に疑いをもったが、[[#代数的な証明|上記]]の 10 を掛ける証明を反対の方向へ用いてみようとした。すると、''x'' = ...999 ならば 10''x'' = ...990 であるから、10''x'' = ''x'' − 9 であり、再び ''x'' = −1 となる。<ref name="Fjelstad11" /> |
|||
最後の拡張として、0.999...=1(実数における等式)と ...999=−1(10-進数における等式)であるから、「盲目的に記号を偽弄することを恥じなければ(by blind faith and unabashed juggling of symbols)」<ref>DeSua p.901</ref> 2つの等式の両辺を加えて ...999.999... = 0 を得る。この等式はもはや 10-進数としても通常の小数展開としても意味をもたないが、よく知られた体系、すなわち実数を表現するために、左方への循環も許す "double-decimals" の理論を誰かが開発すれば、一転してこの等式も意味をもち正しくなる。<ref>DeSua pp.902-903</ref> |
|||
==一般化== |
|||
等式 0.999...=1 の証明は直ちに2つの方法で一般化される。最初に、まさにその特別な場合において考えられたように、すべての 0 でない有限小数 (すなわち、後ろに 0 が限りなく続く) は9 が後ろにずっと続く別表現をもっている。例えば、0.24999... は 0.25 に等しい。これらの数は正確に小数であり、稠密である。<ref>Petkovšek p.408</ref> |
|||
次に、0.999...=1 に相当する結果を他の[[基数]]にも適用することができる。例えば 2 を基数とする([[二進法]])と 0.111...=1 であり、3 を基数とする([[位取り記数法|三進法]])と 0.222...=1 である。実解析の教科書は 0.999...=1 の例を飛ばして、これらの一般化のうちの一つか両方を最初から紹介する傾向がある。<ref>Protter and Morrey p.503; Bartle and Sherbert p.61</ref> |
|||
1 の別表現は、非整数を基数としても現れる。例えば、[[黄金比]]を基数とすると、2つの標準的表示は 1.000... と 0.101010... であるが、他にも0.'''11''', 0.10'''11''', 0.1010'''11''' のように隣接する "1" を含む無数の表現がある。一般的に、1 と 2 の間の [[ほとんどすべての]] ''q'' に対し、"非可算無限" の 『1 の ''q''-進表現』が存在する。 他方で、(1 より大きい自然数を含めた) なお "非可算無限" の ''q'' が 1 の ''q''-進表現を(自明な 1.000... を除いて)ただ一つしかもたない。この結果は 1990 年ごろに [[ポール・エルデシュ]](Paul Erdős)、ミクローシュ・ホルヴァート(Miklos Horváth)、イストヴァン・ヨー(István Joó) によって最初に述べられた。1998 年に Vilmos Komornik とパオラ・ロレティ (Paola Loreti) はこのような最小の基数として ''q'' = 1.787231650... を決定した。この基数においては、1 = 0.11010011001011010010110011010011... であり、この数は[[トゥーエ-モース列]] (Thue-Morse sequence) を与える。これは循環しない。<ref>Komornik and Loreti p.636</ref> |
|||
さらに変則的な規則に基づく記数法 (the most general positional numeral systems) においても0.999 = 1 に相当する結果が得られる。これらもまた多様な表現をもつので、ある意味で扱いはさらに困難である。例えば、<ref>Kempner p.611; Petkovšek p.409</ref> |
|||
*[[平衡三進数]] (balanced ternary system) においては、 <sup>1</sup>/<sub>2</sub> = 0.111... = 1.<u>111</u>... |
|||
*[[階乗進数]] (factoradic system) においては、 1 = 1.000... = 0.1234... |
|||
マルコ・ペトカイゼク (Marko Petkovšek) は、そのように一つの数が複数の方法で表せるということは位取り記数法を用いることの必然的な結果であると述べ、すべての実数を扱う任意の位取り記数法において複数の表現をもつ実数の集合はつねに稠密であることを証明した。彼はこの証明を「一般位相空間に関する初級の教育的な練習問題」と呼んだ。それは、位取り記数法の値の集合を [[Stone空間]]と見ること、その実数表現が[[連続関数(トポロジー)|連続関数]]によって与えられることに気づくことを、その証明が含んでいるからである。<ref>Petkovšek pp.410-411</ref> |
|||
==応用例== |
|||
1 の別表現としての 0.999... に関する一つの応用が[[数論|初等整数論]]に見られる。1802年にグッドウィン (H. Goodwin) はある種の[[素数]]を分母とする分数の循環小数表現に 9 が出現することの所見を発表した。その例は、 |
|||
*<sup>1</sup>/<sub>7</sub> = 0.142857142857… そして 142 + 857 = 999 |
|||
*<sup>1</sup>/<sub>73</sub> = 0.0136986301369863… そして 0136 + 9863 = 9999 |
|||
を含む。 |
|||
ミディ(E. Midy) は 1836 年にこのような分数に関する一般的な結果を証明して、現在は[[ミディの定理]] (Midy's Theorem) と呼ばれている。その論文は曖昧であり、彼の証明が直接 0.999... を含むかどうか定かではない。しかし、レーヴィット (W. G. Leavitt) による少なくとも一つの現代的な証明ではそれが含まれている。もし、0.''b''<sub>1</sub>''b''<sub>2</sub>''b''<sub>3</sub>… という形の小数が正の整数であることを証明できれば、それは 0.999... に他ならず、それがこの定理において 9 たちが出現する原因となる。<ref>Leavitt 1984 p.301</ref> この方向への研究は [[最大公約数]]、[[剰余計算]] (modular arithmetic)、[[フェルマー数#フェルマー素数|フェルマー素数]]、[[群]]の元の[[位数]]、[[2次相互法則]] (quadratic reciprocity) などの概念に動機付けを与える。<ref>Lewittes pp.1-3; Leavitt 1967 pp.669,673; Shrader-Frechette pp.96-98</ref> |
|||
[[Image:Cantor base 3.svg|right|thumb|Positions of <sup>1</sup>/<sub>4</sub>, <sup>2</sup>/<sub>3</sub>, and 1 in the Cantor set]] |
|||
実解析に戻って、三進法での類似表現 0.222… = 1 は最も単純な [[フラクタル]] の一つ [[カントール三進集合]] (the middle-thirds Cantor set) の特徴づけに重要な役割を果たしている。 |
|||
*[[区間|単位区間]] [0,1] の点は、三進数で 0 と 2 のみを用いて表現される場合に限りカントール集合に属するという。 |
|||
小数第 ''n'' 位の数字は、この構成における 第 ''n'' 段階の点の位置に反映する。例えば、点 <sup>2</sup>/<sub>3</sub> は通常の 0.2 または 0.2000... として表現される。なぜなら、それは最初の欠損部分の右側に位置し、それ以後のすべての欠損部分の左に位置するからである。また、点 <sup>1</sup>/<sub>3</sub> は 0.1 ではなく 0.0222... として表現される。なぜなら、それは最初の欠損部分の左側に位置し、それ以後のすべての欠損部分の右側に位置するからである。<ref>Pugh p.97; Alligood, Sauer, and Yorke pp.150-152。Protter と Morrey (p.507) および Pedrick (p.29) はこの記述を練習問題として位置づけている。</ref> |
|||
9 の繰返しはカントールのもう一つの仕事にさえも現れる。彼が 1891 年に[[カントールの対角線論法|対角線論法]]を適用して単位区間 [0,1] の[[基数#可算・連続体|不可算]]性の適切な証明を与えたことを考慮しなければならない。このような証明ではある2つの実数が小数表現において異なることを言明することが必要とされる。したがって、0.2 と 0.1999... のような組を避けなければならない。簡単な方法においては、すべての数を無限小数で表すが、それに対する方法では 9 が最後に連続することを排斥する。<ref>マオール (Maor) (p.60) およびマンキェヴィチ (Mankiewicz) (p.151) は前者の方法を振り返る。マンキェヴィチはそれがカントールの仕事だとしているが、最初の出所は定かではない。Munkres (p.50) は後者の方法に言及している。</ref> カントール独自の議論に近いといえる証明の変形では実際に二進表現を用いており、三進表現を二進表現に変えることによりカントール集合の不可算性を同様に証明することができる。<ref>Rudin p.50, Pugh p.98</ref> |
|||
== 民間における文化 == |
|||
[[インターネット]]の登場に伴い、0.999... に関する論争は教室を抜け出し、 [[ニュースグループ]]や[[掲示板]]において平凡な話題となった。その中には、通常は数学にあまり関係のないニュースグループや掲示板を多く含む。ニュースグループ <tt>[news:sci.math sci.math]</tt> においては、0.999... に関する議論は「流行のスポーツ」であり、それは [[FAQ]] で回答された問題の一つである。<ref>Richman (p.396)が述べている。 {{cite web |url=http://www.faqs.org/faqs/sci-math-faq/specialnumbers/0.999eq1/ |author=Hans de Vreught | year=1994 | title=sci.math FAQ: Why is 0.9999… = 1? |accessdate=6月29日|accessyear=2006年}}</ref> その FAQ は <sup>1</sup>/<sub>3</sub> を用いる方法、10倍する方法、極限を用いる方法を簡潔に扱い、さらには同様にコーシー列にも言及している。 |
|||
一般的に興味をもたれている新聞のコラム ''The Straight Dope'' の2003年版では、誤った概念に関して言及しつつ、 <sup>1</sup>/<sub>3</sub> や極限を通して 0.999... について次のように議論している。 |
|||
:「我々の中の類人猿的要素が、『0.999... は実際に''数'' を表しているのではなく、''過程'' を表している。一つの数を見つけるために我々はその過程を途中で断ち切らなければならない。その時点において 0.999...=1 という概念は崩壊する。』と言って依然として抵抗している。 |
|||
:ナンセンスだ!」<ref>{{cite web |url=http://www.straightdope.com/columns/030711.html |title=An infinite question: Why doesn't .999~ = 1? |date=2003-07-11 |author=Cecil Adams |work=The Straight Dope |publisher=The Chicago Reader |accessdate=9月6日|accessyear=2006年}}</ref> |
|||
''The Straight Dope'' は「他の掲示板...ほとんどがビデオゲーム」から独立した専用の掲示板で議論を載せている。同様の調子で、0.999... の問題は、アメリカのゲーム開発会社ブリザード・エンターテイメント (Blizzard Entertainment) の Battle.net フォーラムで最初の7年間にとても一般的な話題であることがわかったため、その会社の社長 Mike Morhaime は [[2004年]][[4月1日]] の記者会見で 0.999...=1 であると発表した。 |
|||
:「我々はこの問題に対しきっぱりと決着をつけることに大変興奮しています。我々は 0.999... が 1 に等しいのか等しくないのかについての、心痛や心配に立ち会ってきました。ここに次の証明を提示し、我々の顧客に対して、最終的に断固としてこの問題に対処できることを嬉しく思います。」<ref>{{cite web |url=http://www.blizzard.com/press/040401.shtml |title=Blizzard Entertainment® Announces .999~ (Repeating) = 1 |work=Press Release |publisher=Blizzard Entertainment |date=2004-04-01 |accessdate=9月3日|accessyear=2006年}}</ref> |
|||
続く Blizzard のプレスリリース(報道機関向けの発表)では、極限に基づくものと10を掛けるものの2つの証明を提供している。 |
|||
== 関連する問題 == |
|||
<!--[[Intuitionism]] should be worked in somewhere and explained, not necessarily here.--> |
|||
*[[ゼノンのパラドックス]]、とりわけアキレウスと亀のパラドックスは、すぐ理解できるパラドックス 0.999...=1 を連想させる。アキレウスのパラドックスは数学的にモデル化され、0.999... と同じように等比数列を用いて解決される。しかしながら、この数学的な取り扱いがゼノンが探求していた潜在的な形而上の問題に対処しているかどうかは明らかでない。<ref>Wallace p.51, Maor p.17</ref> |
|||
*[[ゼロ除算|0 による除算]] は 0.999... のいくつかの一般的な議論に見られるが、それもまた論争を引き起こす。多くの著者が 0.999... を定義することを選択する一方で、ほとんどすべての現代的な取り扱いでは 0 による除算を定義していない。というのは、それが通常の実数では意味を与えられていないからである。しかしながら、0 による除算は[[複素解析]]など他の体系では定義されている。複素解析では、拡張された複素平面([[リーマン球面]])は[[無限遠点]]をもつ。ここで、<sup>1</sup>/<sub>0</sub> を無限大であると定義することには意味がある。<ref>例えば以下を参照。 J.B. Conway's treatment of Möbius transformations, pp.47-57</ref>また、実際その結果は奥深く、工学や物理学に適用可能である。何人かの著名な数学者は、どの数体系も発達するずっと前からそのような定義を論じていた。<ref>Maor p.54</ref> |
|||
*[[-0|負の 0]] は数を書き表す多くの方法においては、もう1つの冗長な特徴である。実数などの数体系においては、"0" は加法に関する単位元を意味し、正の数でも負の数でもない。通常 "−0" は加法に関する 0 の逆元を表すと解釈され、−0 = 0 でなければならない。<ref>Munkres p.34, Exercise 1(c)</ref> それにもかかわらず、いくつかの科学的な応用では、最も共通なコンピュータの数体系(例えば [[符号つき整数]]、[[1の補数|1 の補数表現]]、[[IEEE754|IEEE 754]] で定義されたような[[浮動小数点数|浮動小数点]]表示)のように、正と負の 0 を分けて用いる。<ref>{{cite book |author=Kroemer, Herbert; Kittel, Charles |title=Thermal Physics |edition=2e |publisher=W. H. Freeman |year=1980 |id=ISBN 0-7167-1088-9 |pages=462}}</ref><ref>{{cite web |url=http://msdn.microsoft.com/library/en-us/csspec/html/vclrfcsharpspec_4_1_6.asp |title=Floating point types |work=[[Microsoft Developer Network|MSDN]] C# Language Specification |accessdate=8月29日|accessyear=2006年}}</ref> IEEE の浮動小数点数の場合は、負の 0 は、与えられた正確な数値を表すには(絶対値が)小さすぎるが、それでもなお負の数である値を表している。したがって、IEEE 浮動点数表示における「負の 0 」は真実の意味で負の "0" ではない。 |
|||
==注== |
|||
<div class="small"> |
|||
<references /> |
|||
</div> |
|||
==参考文献== |
|||
<div class="references-small" style="-moz-column-count: 2; column-count: 2;"> |
|||
*{{cite book |author=Alligood, Sauer, and Yorke |year=1996 |title=Chaos: An introduction to dynamical systems |chapter=4.1 Cantor Sets |publisher=Springer |id=ISBN 0-387-94677-2}} |
|||
*:力学に関するこの入門的な教科書は、学部生または初級の大学院生向けである。(p.ix) |
|||
*{{cite book |last=Apostol |first=Tom M. |year=1974 |title=Mathematical analysis |edition=2e |publisher=Addison-Wesley |id=ISBN 0-201-00288-4}} |
|||
*:微積分学からより進んだ解析学 ''Mathematical analysis'' への変遷が「ごまかさないで、厳密で、最新であると同時に学者ぶることのないように」意図されている。(序文)Apostol は実数の構成に上限の存在公理を用いており、無限小数が2ページ後で紹介されている。(pp.9-11) |
|||
*{{cite book |author=Bartle, R.G. and D.R. Sherbert |year=1982 |title=Introduction to real analysis |publisher=Wiley |id=ISBN 0-471-05944-7}} |
|||
*:このテキストは「実解析の基本的性質と技巧を扱う、理解しやすくてほどよい進度の教科書」を目指している。実数の構成には上限の存在公理を用いている。(pp.vii-viii) |
|||
*{{cite book |last=Beals |first=Richard |title=Analysis |year=2004 |publisher=Cambridge UP |id=ISBN 0-521-60047-2}} |
|||
*{{cite book |author=Berlekamp, E.R.; J.H. Conway; and R.K. Guy |year=1982 |title=Winning Ways for your Mathematical Plays |publisher=Academic Press |id=ISBN 0-12-091101-9}} |
|||
*{{cite journal |last=Berz |first=Martin |title=Automatic differentiation as nonarchimedean analysis |year=1992 |journal=Computer Arithmetic and Enclosure Methods |publisher=Elsevier |pages=439-450 |url=http://citeseer.ist.psu.edu/berz92automatic.html}} |
|||
*{{cite book |last=Bunch |first=Bryan H. |title=Mathematical fallacies and paradoxes |year=1982 |publisher=Van Nostrand Reinhold |id=ISBN 0-442-24905-5}} |
|||
*:この本は、その中心的な話題「数学的な現実性と物理的な現実性のやや希薄な関係」を調べる道具として、パラドックスと誤った推論による解析を紹介している。高校1年生程度の代数を仮定しており、(第2章の等比数列を含めて)さらに進んだ数学はこの本の中で発展していく。 0.999... は完全に扱われているものの一つではないが、カントールの対角線論法を扱うなかで簡潔に述べられている。(pp.ix-xi, 119) |
|||
*{{cite book |last=Burrell |first=Brian |title=Merriam-Webster's Guide to Everyday Math: A Home and Business Reference |year=1998 |publisher=Merriam-Webster |id=ISBN 0-87779-621-1}} |
|||
*{{cite book |last=Conway |first=John B. |title=Functions of one complex variable I |edition=2e |publisher=Springer-Verlag |origyear=1973 |year=1978 |id=ISBN 0-387-90328-3}} |
|||
*:このテキストは必修科目としての「基本的な微積分の厳密な課程」の役割を担っており、述べられているその原則は "An Introduction to Mathematics" として複素解析を紹介し、対象を明確に正確に述べることである。(p.vii) |
|||
*{{cite book |last=Davies |first=Charles |year=1846 |title=The University Arithmetic: Embracing the Science of Numbers, and Their Numerous Applications |publisher=A.S. Barnes |url=http://books.google.com/books?vid=LCCN02026287&pg=PA175}} |
|||
*{{cite journal |last=DeSua |first=Frank C. |title=A system isomorphic to the reals |format=restricted access |journal=The American Mathematical Monthly |volume=67 |number=9 |month=November |year=1960 |pages=900-903 |url=http://links.jstor.org/sici?sici=0002-9890%28196011%2967%3A9%3C900%3AASITTR%3E2.0.CO%3B2-F}} |
|||
*{{cite journal |author=Dubinsky, Ed, Kirk Weller, Michael McDonald, and Anne Brown |title=Some historical issues and paradoxes regarding the concept of infinity: an APOS analysis: part 2 |journal=Educational Studies in Mathematics |year=2005 |volume=60 |pages=253-266 |id={{doi|10.1007/s10649-005-0473-0}}}} |
|||
*{{cite journal |author=Edwards, Barbara and Michael Ward |year=2004 |month=May |title=Surprises from mathematics education research: Student (mis)use of mathematical definitions |journal=The American Mathematical Monthly |volume=111 |number=5 |pages=411-425}} |
|||
*{{cite book |last=Enderton |first=Herbert B. |year=1977 |title=Elements of set theory |publisher=Elsevier |id=ISBN 0-12-238440-7}} |
|||
*:集合論の入門的な学部生用の教科書であり、「特別な予備知識を前提としない」。公理的集合論または数体系の構成に焦点をおいた学習課程を提供するために書かれているが、公理という題材は、あまり重要視されないような方法で扱われている。(pp.xi-xii) |
|||
*{{cite book |last=Euler |first=Leonhard |origyear=1770 |year=1822 |edition=3rd English edition |title=Elements of Algebra |editor=John Hewlett and Francis Horner, English translators. |publisher=Orme Longman |url=http://books.google.com/books?id=X8yv0sj4_1YC&pg=PA170}} |
|||
*{{cite journal |last=Fjelstad |first=Paul |title=The repeating integer paradox |format=restricted access |journal=The College Mathematics Journal |volume=26 |number=1 |month=January |year=1995 |pages=11-15 |url=http://links.jstor.org/sici?sici=0746-8342%28199501%2926%3A1%3C11%3ATRIP%3E2.0.CO%3B2-X |id={{doi|10.2307/2687285}}}} |
|||
*{{cite book |last=Gardiner |first=Anthony |title=Understanding Infinity: The Mathematics of Infinite Processes |origyear=1982 |year=2003 |publisher=Dover |id=ISBN 0-486-42538-X}} |
|||
*{{cite book |last=Gowers |first=Timothy|title=Mathematics: A Very Short Introduction |year=2002 |publisher=Oxford UP |id=ISBN 0-19-285361-9}} |
|||
*{{cite book |last=Grattan-Guinness |first=Ivor |year=1970 |title=The development of the foundations of mathematical analysis from Euler to Riemann |publisher=MIT Press |id=ISBN 0-262-07034-0}} |
|||
*{{cite book | last=Griffiths | first=H.B. | coauthors=P.J. Hilton | title=A Comprehensive Textbook of Classical Mathematics: A Contemporary Interpretation | year=1970 | publisher=Van Nostrand Reinhold | location=London | id=ISBN 0-442-02863-6.}} (LCC QA37.2 G75) |
|||
*:この本は、バーミンガム地方のグラマースクールの数学教師の課程から生まれたものである。この課程は、学校で教えられる数学をもとにして大学レベルの数学への展望を伝えるのが目的であり、「大学で数学の専門課程を1年間学んだ程度のレベル」の生徒向けである。実数の構成は第24章で述べられているが、「おそらくこの本全体の中で最も難しい章」である。しかしながら著者たちはこの難しさをイデアル論を用いているためとしている。イデアル論はここでは扱われていない。(pp.vii, xiv) |
|||
*{{cite journal |last=Kempner |first=A.J. |title=Anormal Systems of Numeration |format=restricted access |journal=The American Mathematical Monthly |volume=43 |number=10 |month=December |year=1936 |pages=610-617 |url=http://links.jstor.org/sici?sici=0002-9890%28193612%2943%3A10%3C610%3AASON%3E2.0.CO%3B2-0}} |
|||
*{{cite journal |author=Komornik, Vilmos; and Paola Loreti |title=Unique Developments in Non-Integer Bases |format=restricted access |journal=The American Mathematical Monthly |volume=105 |number=7 |year=1998 |pages=636-639 |url=http://links.jstor.org/sici?sici=0002-9890%28199808%2F09%29105%3A7%3C636%3AUDINB%3E2.0.CO%3B2-G}} |
|||
*{{cite journal |last=Leavitt |first=W.G. |title=A Theorem on Repeating Decimals |format=restricted access |journal=The American Mathematical Monthly |volume=74 |number=6 |year=1967 |pages=669-673 |url=http://links.jstor.org/sici?sici=0002-9890%28196706%2F07%2974%3A6%3C669%3AATORD%3E2.0.CO%3B2-0}} |
|||
*{{cite journal |last=Leavitt |first=W.G. |title=Repeating Decimals |format=restricted access |journal=The College Mathematics Journal |volume=15 |number=4 |month=September |year=1984 |pages=299-308 |url=http://links.jstor.org/sici?sici=0746-8342%28198409%2915%3A4%3C299%3ARD%3E2.0.CO%3B2-D}} |
|||
*{{cite web | url=http://arxiv.org/abs/math.NT/0605182 |title=Midy's Theorem for Periodic Decimals |last=Lewittes |first=Joseph |work=New York Number Theory Workshop on Combinatorial and Additive Number Theory |year=2006 |publisher=[[arXiv]]}} |
|||
*{{cite journal |last=Lightstone |first=A.H. |title=Infinitesimals |format=restricted access |journal=The American Mathematical Monthly |year=1972 |volume=79 |number=3 |month=March |pages=242-251 |url=http://links.jstor.org/sici?sici=0002-9890%28197203%2979%3A3%3C242%3AI%3E2.0.CO%3B2-F}} |
|||
*{{cite book |last=Mankiewicz |first=Richard |year=2000 |title=The story of mathematics|publisher=Cassell |id=ISBN 0-304-35473-2}} |
|||
*:Mankiewicz は、数学、数学者の著作、歴史的概略の視覚的な側面と質的な側面を組み合わせることによって『理解しやすい形式で数学の歴史』を述べようとしている。(p.8) |
|||
*{{cite book |last=Maor |first=Eli |title=To infinity and beyond: a cultural history of the infinite |year=1987 |publisher=Birkhäuser |id=ISBN 3-7643-3325-1}} |
|||
*:年代順というより話題別の無限に関する回顧。この本は「一般的な読者を意図している」が「数学者の視点から語っている」。数学的な厳密性と読みやすい言葉遣いの板ばさみで、Maor は「この問題を正しく取り扱うことに成功したことを願っている」と述べている。(pp.x-xiii) |
|||
*{{cite book |last=Mazur |first=Joseph |title=Euclid in the Rainforest: Discovering Universal Truths in Logic and Math |year=2005 |publisher=Pearson: Pi Press |id=ISBN 0-13-147994-6}} |
|||
*{{cite book |last=Munkres |first=James R. |title=Topology |year=2000 |origyear=1975 |edition=2e |publisher=Prentice-Hall |id=ISBN 0-13-181629-2}} |
|||
*:形式的な予備知識を必要としないで「大学3~4年生または大学院の1年生レベル」における入門書を意図している。「読者が集合論についてよく知っていることを仮定すらしない。」(p.xi) Munkres の実数の扱いは公理的であり、この道具を持たない構成方法について彼は「このアプローチの方法は多くの時間と努力を必要とし、数学的な興味として扱うよりもはるかに論理的である。」と述べている。(p.30) |
|||
*{{cite book |last=Pedrick |first=George |title=A First Course in Analysis |year=1994 |publisher=Springer |id=ISBN 0-387-94108-8}} |
|||
*{{cite journal |last=Petkovšek |first=Marko |title=Ambiguous Numbers are Dense |format=restricted access |journal= American Mathematical Monthly |volume=97 |number=5 |month=May |year=1990 |pages=408-411 |url=http://links.jstor.org/sici?sici=0002-9890%28199005%2997%3A5%3C408%3AANAD%3E2.0.CO%3B2-Q}} |
|||
*{{cite journal |author=Pinto, Márcia and David Tall |title=Following students' development in a traditional university analysis course |journal=PME25 |pages=v4: 57-64 |year=2001 |url=http://www.warwick.ac.uk/staff/David.Tall/pdfs/dot2001j-pme25-pinto-tall.pdf}} |
|||
*{{cite book |author=Protter, M.H. and C.B. Morrey |year=1991 |edition=2e |title=A first course in real analysis |publisher=Springer |id=ISBN 0-387-97437-7}} |
|||
*:この本は「微積分学の標準的な仮定を終えた生徒に適切な、解析学の理論的構成を紹介する」ことを目標とする。(p.vii) 第2章の終わりで著者は、実数において有界単調列が収束するということを公理として仮定しているが、その後で区間縮小法の原理と上限の存在の性質を証明している。(pp.56-64) 小数展開は Appendix 3 "Expansions of real numbers in any base" に見られる。(pp.503-507) |
|||
*{{cite book |last=Pugh |first=Charles Chapman |title=Real mathematical analysis |year=2001 |publisher=Springer-Verlag |id=ISBN 0-387-95297-7}} |
|||
*:実数のよく知られた性質を仮定する一方で、Pugh はできるだけ早い段階で実数の切断を紹介する。公理的な取り扱いについて「実数の体系に基づいて実数が構成されていることを考えると、これは一つの詐欺である。」と述べている。(p.10) 上限の存在の性質とそれに関係するいくつかの事実を証明した後は、その他の場面で切断は用いられていない。 |
|||
*{{cite journal |first=Fred |last=Richman |year=1999 |month=December |title=Is 0.999… = 1? |format=restricted access |journal=Mathematics Magazine |volume=72 |issue=5 |pages=396-400 |url=http://links.jstor.org/sici?sici=0025-570X%28199912%2972%3A5%3C396%3AI0.%3D1%3E2.0.CO%3B2-F}} Free HTML preprint: {{cite web |url=http://www.math.fau.edu/Richman/HTML/999.htm |first=Fred|last=Richman|title=Is 0.999… = 1? |date=1999-06-08 |accessdate=8月23日|accessyear=2006年}} 注:雑誌の論文にはプレプリントには見られない記述が含まれている。 |
|||
*{{cite book |last=Robinson |first=Abraham |title=Non-standard analysis |year=1996 |edition=Revised edition |publisher=Princeton University Press|id=ISBN 0-691-04490-2}} |
|||
*{{cite book |last=Rosenlicht |first=Maxwell |year=1985 |title=Introduction to Analysis |publisher=Dover |id=ISBN 0-486-65038-3}} |
|||
*{{cite book |last=Rudin |first=Walter |title=Principles of mathematical analysis |edition=3e |year=1976 |origyear=1953 |publisher=McGraw-Hill |id=ISBN 0-07-054235-X}} |
|||
*:より進んだ学部生の課程のための教科書。「有理数から実数を構成する方法からはじめるのは(論理的には正しいけれども)教育上好ましくないことを経験上確信している。初期の段階では、多くの生徒は、このことの必要性についてその価値を認めることができない。それゆえ、実数の体系は、上限が存在する実数体として紹介され、この性質の興味深いいくつかの応用例がすぐになされる。デデキントの構成は無視されている。現在はこれは第1章の Appendix にあり、機が熟したときにいつでも勉強して楽しむことができる。」(p.ix) |
|||
*{{cite journal |last=Shrader-Frechette |first=Maurice |title=Complementary Rational Numbers |format=restricted access |journal=Mathematics Magazine |volume=51 |number=2 |month=March |year=1978 |pages=90-98 |url=http://links.jstor.org/sici?sici=0025-570X%28197803%2951%3A2%3C90%3ACRN%3E2.0.CO%3B2-O}} |
|||
*{{cite book |author=Smith, Charles and Charles Harrington |year=1895 |title=Arithmetic for Schools |publisher=Macmillan |url=http://books.google.com/books?vid=LCCN02029670&pg=PA115}} |
|||
*{{cite book |last=Sohrab |first=Houshang |title=Basic Real Analysis |year=2003 |publisher=Birkhäuser |id=ISBN 0-8176-4211-0}} |
|||
*{{cite book |last=Stewart |first=Ian |title=The Foundations of Mathematics |year=1977 |publisher=Oxford UP |id=ISBN 0-19-853165-6}} |
|||
*{{cite book |last=Stewart |first=James |title=Calculus: Early transcendentals |edition=4e |year=1999 |publisher=Brooks/Cole |id=ISBN 0-534-36298-2}} |
|||
*:この本は「生徒たちが微積分を理解するのを援助」し、「観念に対する理解を育成する」ことを目的としている。(p.v) 微積分の基本性質の証明は省略されている。 |
|||
*{{cite journal |author=D.O. Tall and R.L.E. Schwarzenberger |title=Conflicts in the Learning of Real Numbers and Limits |journal=Mathematics Teaching |year=1978 |volume=82 |pages=44-49 |url=http://www.warwick.ac.uk/staff/David.Tall/pdfs/dot1978c-with-rolph.pdf}} |
|||
*{{cite journal |last=Tall |first=David |title=Conflicts and Catastrophes in the Learning of Mathematics |journal=Mathematical Education for Teaching |year=1976/7 |volume=2 |number=4 |pages=2-18 |url=http://www.warwick.ac.uk/staff/David.Tall/pdfs/dot1976a-confl-catastrophy.pdf}} |
|||
*{{cite journal |last=Tall |first=David |title=Cognitive Development In Advanced Mathematics Using Technology |journal=Mathematics Education Research Journal |year=2000 |volume=12 |number=3 |pages=210-230 |url=http://www.warwick.ac.uk/staff/David.Tall/pdfs/dot2001b-merj-amt.pdf}} |
|||
*{{cite book|last=von Mangoldt|first=Dr. Hans| title=Einführung in die höhere Mathematik|edition=1st ed.|year=1911|publisher=Verlag von S. Hirzel| location=Leipzig|language=German|chapter=Reihenzahlen}} |
|||
*{{cite book |last=Wallace |first=David Foster|title=Everything and more: a compact history of infinity |year=2003 |publisher=Norton |id=ISBN 0-393-00338-8}} |
|||
</div> |
|||
== 関連項目 == |
|||
* [[位取り記数法]] |
|||
* [[実解析]] |
|||
* [[超準解析]] |
|||
== 外部リンク == |
|||
{{commons|0.999...}} |
|||
*[http://www.cut-the-knot.org/arithmetic/999999.shtml .999999... = 1?] from cut-the-knot |
|||
*[http://mathforum.org/dr.math/faq/faq.0.9999.html Why does 0.9999… = 1 ?] |
|||
*[http://www.newton.dep.anl.gov/askasci/math99/math99167.htm Ask A Scientist: Repeating Decimals] |
|||
*[http://descmath.com/diag/nines.html Repeating Nines] |
|||
<!-- *[http://www.steve.bush.org/links/humor/pg001185.html Mathematical Gazette joke] -->*[http://qntm.org/pointnine Point nine recurring equals one] |
|||
*[http://www.warwick.ac.uk/staff/David.Tall/themes/limits-infinity.html David Tall's research on mathematics cognition] |
|||
{{Link FA|en}} |
|||
<!--[[category:数の表現|0.999...]] |
|||
[[Category:数学に関する記事|0.999...]] |
|||
書式がよくわからないのでとりあえずコメントアウトしておきます。修正をお願いします。--> |
|||
[[en:0.999...]] |
|||
[[be:0,(9)]] |
|||
[[el:0,999...]] |
|||
[[es:0,9 periódico]] |
|||
[[fr:Développement décimal de l'unité]] |
|||
[[de:Eins]] |
|||
[[ka:0.999...]] |
|||
[[nov:0.999...]] |
|||
[[pl:0,(9)]] |
|||
[[pt:0,999...]] |
|||
[[ro:0,(9)]] |
|||
[[ru:0,(9)]] |
|||
[[sl:0,999...]] |
|||
[[fi:0,999...]] |
|||
[[sv:0,999...]] |
|||
[[th:การพิสูจน์ว่า 0.999... เท่ากับ 1]] |
|||
[[zh:证明0.999...等于1]] |
|||
2007年1月19日 (金) 16:01時点における版

数学においては、 循環小数で 0.999... と書かれる実数は 1 と 完全に 等しい("0.999..." は または などとも書かれる) 。 換言すれば、 "0.999..." は "1" という記号と同じ数を表している。この等式に関するさまざまな 証明が、厳密性、望ましいと思われる実数の研究結果、前提条件や歴史的背景、さらには対象となる読者、というそれぞれの多様性に応じて練り上げられてきた。
この等式は長い間教科書において指導されてきており、ここ数十年間、数学教育の学者によりこの等式に対する生徒の反応が研究されているが、生徒はしばしばこの等式を受け入れない。生徒たちの推論は、概して実数に関するいくつかの共通の誤った直観に基づいている。それは、例えば、一つ一つの小数展開がただ一つの数に対応するに違いないという考えであったり、無限小という量が存在するという期待であったり、算数が崩壊するという予想であったり、極限が理解する能力の欠如であったりする。もしくは、単に 0.999… には "最後の 9" があると考えているだけかもしれない。これらの考えは、実数に関しては正しくないが、これは有理数から実数を系統立てて構成することにより証明可能であり、また、そのような構成方法から 0.999...= 1 であることを直接証明することができる。同時に、直観によって想像される現象のいくつかは他の数体系においても起こりうる。さらに、"0.999..." と書ける対象が厳密に 1 より小さくなる数体系すらある。
1 という数が2つの小数展開をもつということは、十進法に限った特殊性ではない.同様の現象が 10 以外の整数を基数とする場合にも起こる。さらに、数学者たちは非整数を基数として1を書き表す方法が何通り考えられるかについても研究してきた。また、この現象は 1 という数に限ったことではない。すべての 0 でない有限小数は後に 9 が続く別表現をもっている。簡単のため通常は、有限小数で表す方が好まれるが、さらに言えばこのことが「有限小数がたった一つの表現方法である」という誤解を招く原因ともなりうる。実際、無限小数展開が許されると、すべての位取り記数法はあいまいな数たちを無数に含むことになる。このように1つの数がさまざまな方法で表されるということは、小数の十進展開のパターンやカントール集合とよばれる単純なフラクタルの構造をよりよく理解するために適用されてきた。また、それらは実数全体の集合の無限性に対する古典的な研究の際にも起こっている。
0.999... とは何か
0.999... は十進法で書かれた数であり、これが 1 に等しいという最も単純な証明のいくつかは、この記数法の便利な算術的性質に依存している。 十進小数のほとんどの計算(加法,減法,乗法,除法,比較)が整数の場合と同じ "桁レベルの操作" により為されている。また、整数の場合と同様に、ある桁が異なる任意の2つの有限小数は(あとに 0 がずっと続く場合を無視して)異なる数を表す。特に、"0.999...9" と表される任意の数(9は有限個)は厳密に 1 より小さい。
省略記号 "..." の意味は厳密に特定されなければならない。ここでの "..." の用法は、言語もしくは 0.999...9 における "..." の用法とは異なる。後者の用法は、有限な部分を明言しなかったり省略したりする用法である。循環小数に対して用いるときには、"..." はある無限な部分を明言しないことを意味する。特に、0.999... は数列 {0.9, 0.99, 0.999, 0.9999, ...} の極限(これは、k= 1, 2, 3, ..., ∞ に対し 9 × 0.1k の形をしたすべての項の和に等しい)を表している。0.999... の誤った解釈は、これが 1 に等しいことに関する誤解の原因となる。
等式 0.999...=1 の証明はいろいろある。これを代数的に示す前に、『2つの実数が等しいのは、これらの差(の絶対値)が(第3の)正の実数に等しくない場合に限る』ことに注意する。1 と 0.999... との距離は、任意に与えられた任意の正の数より小さい(これは上記の数列で定義される閉区間と三角不等式を用いて形式的に証明できる)。したがって、この距離は 0 であり、1 と 0.999... は等しい。このことを用いると 例えば 0.333... = 1/3 である理由も説明することができる。
整数や有限小数の場合と異なり、それ以外の表記法は1つの数をいくつかの方法で表すことができる。例えば、分数を用いると、 1/3 = 2/6 となる。 しかしながら、無限小数は1つの数を高々2つの方法でしか表すことができない。もし、2つの方法があったとすると、そのうちの1つは最後に 9 が無限に続く形であり、もう1つは有限で終わる形である(すなわち、あるところから先は 0 が繰り返す列からなる)。
桁ごとの操作
分数を用いた証明
無限小数が有限小数の必然的な拡張である1つの理由は、分数を表現することである。筆算を用いると 1/3 のような、整数の単純な割り算が循環小数 0.333... となる。ここで 3 は終わることなく永遠に続く。 この小数を用いて、0.999...=1 を即座に証明することができる。3と3の積は各桁に 9 を生ずるので、 3 × 0.333… は 0.999 に等しい.一方、1/3 は 1 である。したがって 0.999...=1 である。[1] この証明の別の形として、1/9 = 0.111… に 9 を掛けることもできる。
代数的な証明
もう一つの証明はもっと簡潔に他の循環小数にも適用できる。十進法で表現された数に 10 を掛けると、数字は変化することなく、小数点が1つ右に移動する。ゆえに 10 × 0.999… は 9.999… に等しく、これはもとの数に比べて 9 大きい。このことを見るために、0.999... を 9.999... から引くときに、引き算が桁ごとに扱えるとみなすと、小数点以下各桁において、その結果は 9−9 すなわち 0 である。ところが、小数点のあとに永遠に続く 0 は数を変化させないので、この差はまさしく 9 である。最後の段階では代数を用いる。問題の小数 0.999... を c と呼ぶ。すると、 10c − c = 9 であり、これは 9c = 9 と同値である。両辺を 9 で割ることにより、c=1 が得られ、証明が完了する。 [1] 数式を用いて書くと以下のようになる。
以上2つの証明における桁ごとの操作の正当性は、鵜呑みにしたり、自明の理と見なしたりする必要はない。このことは "小数"と "小数が表す数" の間の基本的な関係を調べることによって証明することができる。 有限小数に関しては、この過程は実数の計算法則にのみ依存している。 この操作が無限小数にも適用できることを証明するためには、実解析の手法を必要とする。
実解析
0.999... の問題は数学の形式的な発展には影響を与えないので、これは実解析の基本的な定理や命題が証明されるまで後回しにすることができる。1つの要請は十進法で表現される実数を特徴づけることである。これは、『符号、整数部分を形成する任意個数の数字の有限列、小数点、そして小数部分を形成する数字の列』から構成される。 0.999... を議論する目的においては、整数部分は b0 とまとめうる。また、負の数は考えなくてよいので、小数展開は
の形である。整数部分と違って、小数部分は有限の桁数に制限されないことが肝心である。これは 位取り記数法であるから、500 における "5" は 50 における "5" の10倍の大きさに寄与する。また、0.05 における "5" は 0.5 における "5" の 1/10 倍の大きさに寄与する。
無限数列と無限級数
おそらく、小数展開の最も一般的な成果は、小数展開を無限数列の和として定義することである。一般的には
と表される。
0.999... に対しては無限等比級数に関する有力な収束定理 [2]
- ならば
を適用することが可能である。
0.999... はこの和において公比を としたものであるから、この定理により
と簡単に問題を解決することができる。この(実際には 10=9.999... の)証明は早くも 1770 年のレオンハルト・オイラーによるElements of Algebra[3] において見られる。
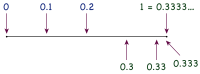
等比数列の和の公式それ自身はオイラー以前の成果である。代表的な18世紀の導出法においては上記の証明と同じような項ごとの操作を用いていた。1811年になってやっと、Bonnycastle の教科書 An Introduction to Algebra では等比級数に関するこのような議論が 0.999... と同様の「巧妙な操作」を正当化するために用いられている。[4] このような寛大な求和法に対抗した19世紀の反動により「無限数列の和はその部分和の極限として定義される」という、現在においても支配的な定義が生み出された。この定理に相当する証明ではこの数列を系統だてて計算しており、それは証明に基づいた微積分学や解析学の入門書に見られる。[5]
数列 {x0, x1, x2, …} は n が増加するにしたがって距離 | x − xn | が 0 に近づくとき極限 x をもつ。 等式 0.999...=1 自身は以下のように極限として表すことにより証明される。
最後のステップ ( lim 1/10n = 0 ) は、実数が アルキメデス性 (Archimedean property) をもつという公理を用いて説明される。また、極限に基づく 0.999... に対するこの姿勢は、幾分わかりやすいがいくらか不正確な言葉を用いて説明されることがある。例えば、1846年の教科書 The University Arithmetic は「0.999...と無限に続く数は1である。なぜなら 9 を積み重ねるたびにその値は 1 に近づくからである」と説明しており、1895年の Arithmetic for Schools は「9 を十分多く用いれば、1 と 0.999... の距離は驚くほど小さい値である」と説明している。[7] このような発見的指導法においては、生徒に「0.999...それ自身は 1 より小さい」という印象をもたせがちである。詳しくは 後述。
区間縮小法と上限
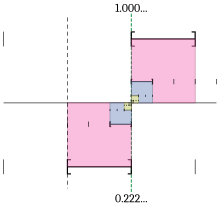
前述の級数による定義は小数展開によって実数を定義する簡単な方法である。もう一つのアプローチは逆の手順をたどるものである。すなわち、先に実数を与え、その実数を表す小数展開を定義する方法である。
実数 x が 閉区間 [0, 10] (すなわち 0 以上 10 以下)に属することが知られているとする。ここでこの区間を、端点のみで重なる 10 個の区間 [0, 1], [1, 2], [2, 3], ... , [9, 10] に分割する。実数 x はこのうちの少なくとも1つの区間に属する。例えば、それが区間 [2, 3] に属するときには、数字 "2" を記録することにする。さらにこれを [2, 2.1], [2.1, 2.2], …, [2.8, 2.9], [2.9, 3] なる区間に分割する。この操作を繰り返すと b0, b1, b2, b3, … という無限数列により名づけられた縮小区間が生じ、
- x = b0.b1b2b3…
と記録される。
この表現形式に従えば、実数 1 は区間 [0, 1] と区間 [1, 2] のいずれにも属し、数字を選ぶときにどちらの区間を選ぶこともできるので、1=1.000... と 1=0.999... の2通りの表現が得られることになる。この表現形式が記号 "=" の濫用でないことを保証するためには、それぞれの小数に対し唯一の実数を構成しなおす方法が必要になる。このことは極限を用いてなされるが、順序の議論を続ける別の構成方法もある。[8]
区間縮小法の原理を用いるのが率直な方法である。この原理によれば、閉区間の無限減少列が与えられ、その幅が 0 に収束するとき、それらの区間の共通部分がただ1つの実数であることが保証される。したがって b0.b1b2b3… はすべての区間 [b0, b0 + 1], [b0.b1, b0.b1 + 0.1], ... に属する唯一の実数であると定義される。したがって 0.999... は [0, 1], [0.9, 1], [0.99, 1], ... , [0.99…9, 1] と、任意個の 9 を含むすべての区間に属する唯一の実数である。一方、実数 1 はこれら1つ1つの区間に属するので 0.999… = 1 となる。[9]
『区間縮小法の原理』は通常、実数に関するもっと基本的な特徴である 上界 (least upper bound, suprema) の存在に基づいている。 これらの事実を直接的に用いると、b0.b1b2b3... を 近似値の集合{b0, b0.b1, b0.b1b2, ...} の上界として定義することができる。[10] この定義(または区間縮小法による定義)は区間分割の手続きと矛盾がないことが示せるので再び 0.999...=1 を得る。 トム・アポストルは次のように結論した。
教育における懐疑主義
数学を学ぶ生徒は 0.999... と 1 が等しいことをしばしば受け入れない。その理由は彼らの本質的に異なる状況から 極限の概念に対する深い懐疑心、そして無限小の性質の拒絶まで多岐にわたる。この困惑に寄与する多くの共通な要因がある。
- 生徒はしばしば、「一つの数はただ1つの小数で表すことができるという信念に精神的に縛られている」。明白に異なる2つの小数が同じ数を表すことを知ると、それは逆説であるように見える。見かけ上よく知られた数 1 の登場がその感情をさらに強める。[12]
- "0.999..." (または同様の表現)を、多いけれども有限の個数の "9" の列(おそらく可変であり特定できない長さ)として解釈する生徒もいる。たとえ生徒が "9" の無限個の列であることを受け入れたとしても、まだ最後の "9" が「無限の彼方に」あると期待しているかもしれない。[13]
- 直観的であいまいな指導により、生徒は数列の極限を、一つの決まった値ではなくある種の無限操作と考えるようになる。それは数列の各項はその極限に達する必要はないからである。生徒が数列とその極限の違いを受け入れても、彼らは "0.999..." を極限ではなく数列を意味するものと読む可能性がある。[14]
- 0.999... を 1 よりもごく僅かだけ小さい、固定された値であるとみなす生徒もいる。
- 収束列の値を実際の値ではなく近似値であると信じている生徒もいる。
これらの考えは、通常の実数を扱う文脈においては誤っている。しかしながら、一般的な数学的道具として発明された、もしくは、0.999... を理解するのに有益な反例としての、より精巧な構造においてはそれらの考えの多くが部分的に正しいことが示される。
このような説明の多くはデビット・トール (David Tall) 教授により発見された。教授は、自らが遭遇した大学生の誤解のいくつかについて、それを生徒に抱かせる原因となった指導法と認識の特徴を研究している。非常に多くの生徒がなぜ最初はこの等式を受け入れないのかを調べるために生徒を面接して、次のようなことを発見した。「生徒は 0.999... を、決まった値ではなく 1 に限りなく近づく数の列として理解し続けようとする。その原因は『先生は小数点以下の桁数がいくつあるかをはっきりと教えてなかった』という指導法の欠陥または『0.999... は 1 より小さい数の中で、存在しうる、1 に最も近い小数である』という認識である。」[15]
基本的な証明の中で 0.333...=1/3 の両辺を3倍する方法は、0.999...=1 であることを受け入れない生徒に有無を言わせないための、明らかに成功する戦略であるかのように見える。しかしながら、第1の等式を信じることと、第2の等式を信じないことの矛盾に直面すると、今度は第1の等式を疑い始める生徒もいるし、または単に不満を抱くだけの生徒もいる。[16] これより進んだ方法で簡単に分かるものもまたない。厳密な定義を十分適用する能力のある生徒が、0.999... を含めてさらに進んだ数学の結果に驚いたとしても、なお直観的な想像に頼ってしまうことがある。例えば、ある解析学を学ぶ生徒は 0.333...=1/3 であることを 上限の定義を用いて証明することができるが、その後もなお、昔の筆算の理解に基づいて 0.999...<1 であると主張した。[17] 別の生徒は、1/3=0.333... であることを証明することができるが、分数を用いた証明に直面して「論理」が数学の計算を征服していると主張する。
ジョセフ・メイザー (Joseph Mazur) は別の才能豊かな微積分学の生徒について語る。その生徒は「私が授業で言ったことにはほとんどすべて異議を唱えるが、自分の使っている計算機には決して異議を唱えない」。さらに、23 の平方根を計算することも含めて、数学をするのに必要なのは 9 桁(程度)だと信じるようになった。その生徒は 9.999...=10 であるという極限の議論に相変わらず不愉快な感じを抱いていたが、それは「乱暴な推測をする、無限概念の成長過程(wildly imagined infinite growing process)」と呼ばれる。[18]
エド・デュビンスキー (Ed Dubinsky) による数学学習の理論 (APOS theory)の一部分として、デュビンスキーとその共同研究者 (2005) は、 0.999... を「1 から無限に小さい距離だけ離れている数を表す有限で不確定の文字列」であると思う生徒は「無限小数の構成過程の完全な概念がまだ形成されていない」と述べた。 たとえ 0.999... の構成過程の完全な概念を身につけた生徒であっても、まだその過程を(既に持っている "1" の概念と同様の)一つの「対象」としてとらえ直すことができずに、0.999... という一つの過程と 1 という数の存在を矛盾するものととらえるかもしれない。デュビンスキーらはまた、「一つの対象としてとらえ直す」というこの精神的能力が、1/3 それ自体を数と見なしたり、自然数の集合それ自身を一つの対象として取り扱ったりすることと関係していると考える。[19]
実数
他のアプローチでは、公理的集合論を用いて、有理数をもとにして構造が確かな実数を構成し、それを系統だてて定義する。自然数 (0, 1, 2, ...) は 0 から始まり増加していく数であり、すべての数は『次の数 (successor)』を持っている。自然数にその −1 倍を付け加えて拡張することによってすべての 整数が得られる。 さらに比に拡張し、有理数を得る。これらの数体系は、加法、減法、乗法、除法の算法を伴っている。さらに巧妙に、そこには距離が定義されており、ある数が別の数に比べて小さい、大きい、または等しいなどの判断ができる。
有理数から実数への拡張が重要なステップである。このステップを達成するためには少なくとも2つの一般的な方法がある。ともに 1872年に発表された実数の切断 (Dedekind cut) とコーシー列 (Cauchy sequence) である。これらの構成法を直接的に用いて 0.999...=1 であることを証明している実解析の教科書は見られない。ここ数十年の傾向は、公理的に解析学を記述することである。実数の構成が提供されたときでさえ、それは実数の公理を証明するために用いられ、その上で公理的解析論による証明を支持している。しかしながら、著者の中には、実数の構成から始めることをもっと適切に、もっと論理的に行うことにより、証明すべき結果はもっと直接的になされる(self-contained)という考えを主張する人もいる。[20]
実数の切断
実数の切断のアプローチにおいては、それぞれの実数 x は、それより小さいすべての有理数からなる無限集合である。[21] 特に、実数 1 は 1 より小さいすべての有理数の集合である。[22] 実数の切断により、正の数の小数展開が簡単に決定できる。すなわち、小数展開表示を、ある段階の表示より小さい有理数の集合として定義するのである。したがって、実数 0.999... は r < 0, r < 0.9, r < 0.99, ... のどれかを満たす有理数 r の集合として定義する。一般的には、ある n に対して、 1 − (1/10)n の形の数より小さい有理数の集合として定義する。[23] 0.999... のすべての元は 1 より小さいので、これは実数 1 の元である。逆に、実数 1 の元は 1 より小さい有理数 a/b であり、したがって a/b < 1 − (1/10)b となる。0.999... と 1 は全く同じ有理数を含むので、これらは同じ集合であり、0.999...=1 である。
実数の切断による実数の定義は、最初 1872 年にリヒャルト・デーデキントによって発表された。[24] 上記の、実数をそれぞれの小数展開に帰着させる方法は、フレッド・リッチマン (Fred Richman) の "Is 0.999...= 1?" という説明的な論文による。これは Mathematics Magazine に投稿されているが、これは数学を学ぶ学部生を対象としている。[25] リッチマンは、有理数の任意の稠密な部分集合における切断を考えても同様な結果をもたらすことを注意している。特に彼は小数を用いたが、それにより証明はもっと直接的になる。「したがって、実数の伝統的な定義によれば、等式 0.9...=1 は最初から築かれている。」[26] Richman は、この手順をさらに修正して別の構造を導いており、それについて興味深く論じている。それについては以下の 「「他の数体系」」 を参照。
コーシー列
実数を構成するもう1つの方法は、有理数の順序をもっと間接的に用いることである。最初に,x と y の距離は絶対値 | x − y | として定義できる。ここに、絶対値 | z | は z と −z の小さくない方として定義されていて、したがって負にはならない。すると実数は、この距離を用いたコーシー列という有理数の列であると定義することができる。コーシー列とは、自然数から有理数への写像、数列 (x0, x1, x2, ...) において、任意の正の数 δ に対して、N が存在し、以下の条件を満たす: N より大きいすべての m, n に対して | xm − xn| ≤ δ が成り立つ(2項間の距離が次第に小さくなる)ものである。[27]
数列 (xn) と (yn) が2つのコーシー列であるとき、(xn − yn) が極限 0 をもつならば、これらのコーシー列は実数として等しいと定められる。小数 b0.b1b2b3... を各桁で順に切捨てていくことにより、有理数からなるコーシー列が得られ、その真の値が定義される。[28] こうしてこの形式で、有理数の数列
が極限 0 をもつことを示すことになる。したがって、n=0, 1, 2, ... に対してこの数列の第 n 項を考えると、
であることを示さなければならない。
最後の極限は簡単であり[29]、例えば数列の極限の定義において、 ε = a/b > 0 に対し N = b をとることにより示される。したがって,再び 0.999...=1 を得る。
コーシー列としての実数の定義については、最初に(いずれも)1872 年に エドゥアルト・ハイネ と ゲオルク・カントール により独立に発表された。[24] 0.999...=1 の証明も含めて、小数展開による上記のアプローチは 1970 年に グリフィス (Griffiths) とヒルトン (Hilton) の書いた A comprehensive textbook of classical mathematics: A contemporary interpretation を厳密にたどっている。この本はよく知られた概念を現代の観点でもう一度見直してもらうために特定して書かれている。 [30]
他の数体系
実数は非常に便利な数体系を形成しており、"0.999..." という表記法が実数を意味するものと考えることは根本的には『慣習』である。ウィリアム・ティモシー・ガワーズ (William Timothy Gowers) は Mathematics: A Very Short Introduction において、等式 0.999...=1 を結論することも同様に『慣習』であると述べている。すなわち、
- 「しかしながら、それは決して独裁的な慣習ではない。なぜなら、それを受け入れなければ、一風変わった新しい対象を発明するか、または算数のよく知られた規則のいくつかを諦めるかのどちらかが強制されるからである。」[31]
新しい対象もしくは知られていない規則を用いて上の証明を再び解釈すると、0.999...≠1 であるような仮説の数体系に制限を加えることができる。リッチマンが述べたように、『ある人の証明は、別の人にとっては背理法である。(one man's proof is another man's reductio ad absurdum.)』 [32] もし、 0.999... が 1 と異なれば、上の証明で立てられた少なくとも1つの仮定は潰れなければならない。
無限小
0.999...=1 のいくつかの証明は、通常の実数がアルキメデス的であること、すなわち、"0でない無限小は存在しない" ことに依存している。 通常の実数に代わるいくつかのものを含むような、数学的に理路整然とした順序の導入された代数構造があるが、それは非アルキメデス的である。例えば、二元数は新しい無限小の要素 ε を含む。これは ε2 = 0 であることを除けば 複素数 における虚数単位 i の類似である。結果として生じる構造は、記号処理系のための微分の理論 (automatic differentiation) で有用である。二元数には辞書式順序を与えることができ、この場合において ε の倍数は非アルキメデス的要素になる。[33] 実数に代わる構造を構成するもう一つの方法は、(特殊な例ではあるが)集合論や古典的な理論ではなく、トポス理論やそれに代わる諸論理を用いることである。例えば、『滑らかな無限小解析(smooth infinitesimal analysis)』 では逆元のない無限小が存在する。[34]
超準解析によってたくさんの無限小量(やその逆数)を含んだ体系が得られることはよく知られているが、これによって、普通とは異なり、しかもより直感的と思われる微積分へのアプローチが可能になる。[35] 1972年にライトストーン (A.H. Lightstone) は超準解析に基づき、(0, 1) に属する超実数に対して一意的な "超小数展開" を対応させる考え方を展開した。ここで超小数展開とは超自然数で添字づけられた数字の列のことである。この枠組みにおいて、素朴には0.333... に対応する表示を2種類考えることができるが
- 0.333...;...000... は正確には超小数と見なすことができないが
- 0.333...;...333... はちょうど1⁄3と一致する
のでいずれにせよ0.333...と1⁄3の差は無限小ですらない。[36]
組合せゲーム理論も同様に、とくに関連のある一つの例として "無限二色ハッケンブッシュゲーム (infinite Blue-Red Hackenbush)" をもつ実数の代替構造を与える。1974年に、エルウィン・バールカンプ (Elwyn Berlekamp) はデータ圧縮のアイディアに刺激されて ハッケンブッシュ文字列と実数の2進展開の関係について述べた。例えば、"ハッケンブッシュ文字列 (Hackenbush string)" LRRLRLRL... の値は 0.010101... = 1/3 である。しかしながら、文字列 LRLLL... (0.111...に対応する) の値は 1 に比べてごくわずかだけ小さい。 これらの2数(LRLLL... と 1)の差は 超実数 (surreal number) 1/ω (ω は最初の 無限序数(infinite ordinal) ) である。これに関連するゲームは LRRRR… すなわち 0.000… である。[37]
減法の崩壊
証明が崩されてしまうもう一つのパターンは単に 1 − 0.999… が存在しないのかどうか、という点である。なぜなら、減法は必ずしも可能でないからである。加法の演算をもつが、減法をもたない数学的構造は、可換半群、可換モノイド、半環 (semiring) を包括している。リッチマンは 0.999...<1 となるようにデザインされた、そのような2つの構造を考えた。
まず、リッチマンは負でない decimal number を文字通り小数展開となるように定義する。彼は辞書式順序と加法を定義した。ここでは 0.999... < 1 であることに注意する。なぜなら単に、一の位において 0 < 1 となるからである。しかし、どんな「無限小数」 x に対しても 0.999... + x = 1 + x である。だから、decimal number に特徴的な一つのことは、加法が必ずしも打ち消しあわないということであり、もう一つは 1/3 に対応する decimal number は存在しないということである。乗法を定義すると、decimal number は正値全順序可換半環をなす。[38]
乗法を定義する際、リッチマンはまた、"cut D" と呼ばれる別の構造を定義する。これは小数の切断の集合である。通常この定義は実数を導くが、彼は小数 d に対して、切断(−∞, d ) と "principal cut" (−∞, d ] の両方を許す。その結果、実数たちは小数と「不安定な状態で共存する(living uneasily together with)」ことになる。したがって、再び 0.999... < 1 を得る。"cut D" には正の無限小は存在しないが、"一種の負の無限小" 0− が存在する。0− には小数展開は存在しない。彼は0.999... = 1 + 0− であると結論したが、一方、方程式 "0.999... + x = 1" は解をもたない。[39]
p-進数
1 − 0.999... は何かと尋ねられると、生徒たちは数 "0.000...1" をしばしば発明する。これが意味を持つと持たないとにかかわらず、直観的な到達点は明らかである。すなわち、0.999... の "最後の 9" に 1 を足すことですべての 9 が 0 に変わって上の桁に送られ、一の位に 1 を残す、ということである。他の理由もあって、この考え方は正しくない。なぜなら 0.999... には "最後の9" がないからである。[40] 『最後の9』を持つ無限な文字列を探すためには、どこか他のところを見なければならない。
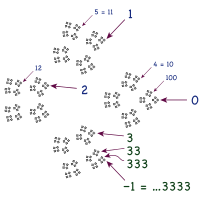
p-進数は整数論で興味がもたれている実数に代わる数体系である。実数と同様に、p-進数はコーシー列を経由して有理数から作ることができる。ただしこの構成には、0 は 1 よりも p に近く、pn にはもっと近いという、普通と異なった距離を用いる。p-進数は素数 p に対しては体をなし、他の p (10 を含む)に対しては環をなす。したがって,p-進数に計算を実行することができ、無限小は存在しない。
『10-進数』は小数展開の類似であり、左の方へ進んでいく。10-進展開 ...999 はまさに "最後の 9" をもつが、"最初の9" はもたない。一の位に 1 を加えることができるが、すると 0 だけが残されて繰り上がりが続き、その結果 1 + ...999 = ...000 = 0 となる。すなわち、...999 = −1 である。[41] もう一つの誘導の仕方は等比級数を用いる。"...999" の意味をもつ無限等比級数は実数においては収束しないが、10-進数では収束し、よく知られた公式を再び用いることができて
となる。(前述の等比級数と比較せよ。)3番目の誘導方法はある中学1年生によって発明された。その生徒は教師が 0.999...=1 を極限を用いて行った議論に疑いをもったが、上記の 10 を掛ける証明を反対の方向へ用いてみようとした。すると、x = ...999 ならば 10x = ...990 であるから、10x = x − 9 であり、再び x = −1 となる。[41]
最後の拡張として、0.999...=1(実数における等式)と ...999=−1(10-進数における等式)であるから、「盲目的に記号を偽弄することを恥じなければ(by blind faith and unabashed juggling of symbols)」[43] 2つの等式の両辺を加えて ...999.999... = 0 を得る。この等式はもはや 10-進数としても通常の小数展開としても意味をもたないが、よく知られた体系、すなわち実数を表現するために、左方への循環も許す "double-decimals" の理論を誰かが開発すれば、一転してこの等式も意味をもち正しくなる。[44]
一般化
等式 0.999...=1 の証明は直ちに2つの方法で一般化される。最初に、まさにその特別な場合において考えられたように、すべての 0 でない有限小数 (すなわち、後ろに 0 が限りなく続く) は9 が後ろにずっと続く別表現をもっている。例えば、0.24999... は 0.25 に等しい。これらの数は正確に小数であり、稠密である。[45]
次に、0.999...=1 に相当する結果を他の基数にも適用することができる。例えば 2 を基数とする(二進法)と 0.111...=1 であり、3 を基数とする(三進法)と 0.222...=1 である。実解析の教科書は 0.999...=1 の例を飛ばして、これらの一般化のうちの一つか両方を最初から紹介する傾向がある。[46]
1 の別表現は、非整数を基数としても現れる。例えば、黄金比を基数とすると、2つの標準的表示は 1.000... と 0.101010... であるが、他にも0.11, 0.1011, 0.101011 のように隣接する "1" を含む無数の表現がある。一般的に、1 と 2 の間の ほとんどすべての q に対し、"非可算無限" の 『1 の q-進表現』が存在する。 他方で、(1 より大きい自然数を含めた) なお "非可算無限" の q が 1 の q-進表現を(自明な 1.000... を除いて)ただ一つしかもたない。この結果は 1990 年ごろに ポール・エルデシュ(Paul Erdős)、ミクローシュ・ホルヴァート(Miklos Horváth)、イストヴァン・ヨー(István Joó) によって最初に述べられた。1998 年に Vilmos Komornik とパオラ・ロレティ (Paola Loreti) はこのような最小の基数として q = 1.787231650... を決定した。この基数においては、1 = 0.11010011001011010010110011010011... であり、この数はトゥーエ-モース列 (Thue-Morse sequence) を与える。これは循環しない。[47]
さらに変則的な規則に基づく記数法 (the most general positional numeral systems) においても0.999 = 1 に相当する結果が得られる。これらもまた多様な表現をもつので、ある意味で扱いはさらに困難である。例えば、[48]
- 平衡三進数 (balanced ternary system) においては、 1/2 = 0.111... = 1.111...
- 階乗進数 (factoradic system) においては、 1 = 1.000... = 0.1234...
マルコ・ペトカイゼク (Marko Petkovšek) は、そのように一つの数が複数の方法で表せるということは位取り記数法を用いることの必然的な結果であると述べ、すべての実数を扱う任意の位取り記数法において複数の表現をもつ実数の集合はつねに稠密であることを証明した。彼はこの証明を「一般位相空間に関する初級の教育的な練習問題」と呼んだ。それは、位取り記数法の値の集合を Stone空間と見ること、その実数表現が連続関数によって与えられることに気づくことを、その証明が含んでいるからである。[49]
応用例
1 の別表現としての 0.999... に関する一つの応用が初等整数論に見られる。1802年にグッドウィン (H. Goodwin) はある種の素数を分母とする分数の循環小数表現に 9 が出現することの所見を発表した。その例は、
- 1/7 = 0.142857142857… そして 142 + 857 = 999
- 1/73 = 0.0136986301369863… そして 0136 + 9863 = 9999
を含む。
ミディ(E. Midy) は 1836 年にこのような分数に関する一般的な結果を証明して、現在はミディの定理 (Midy's Theorem) と呼ばれている。その論文は曖昧であり、彼の証明が直接 0.999... を含むかどうか定かではない。しかし、レーヴィット (W. G. Leavitt) による少なくとも一つの現代的な証明ではそれが含まれている。もし、0.b1b2b3… という形の小数が正の整数であることを証明できれば、それは 0.999... に他ならず、それがこの定理において 9 たちが出現する原因となる。[50] この方向への研究は 最大公約数、剰余計算 (modular arithmetic)、フェルマー素数、群の元の位数、2次相互法則 (quadratic reciprocity) などの概念に動機付けを与える。[51]

実解析に戻って、三進法での類似表現 0.222… = 1 は最も単純な フラクタル の一つ カントール三進集合 (the middle-thirds Cantor set) の特徴づけに重要な役割を果たしている。
- 単位区間 [0,1] の点は、三進数で 0 と 2 のみを用いて表現される場合に限りカントール集合に属するという。
小数第 n 位の数字は、この構成における 第 n 段階の点の位置に反映する。例えば、点 2/3 は通常の 0.2 または 0.2000... として表現される。なぜなら、それは最初の欠損部分の右側に位置し、それ以後のすべての欠損部分の左に位置するからである。また、点 1/3 は 0.1 ではなく 0.0222... として表現される。なぜなら、それは最初の欠損部分の左側に位置し、それ以後のすべての欠損部分の右側に位置するからである。[52]
9 の繰返しはカントールのもう一つの仕事にさえも現れる。彼が 1891 年に対角線論法を適用して単位区間 [0,1] の不可算性の適切な証明を与えたことを考慮しなければならない。このような証明ではある2つの実数が小数表現において異なることを言明することが必要とされる。したがって、0.2 と 0.1999... のような組を避けなければならない。簡単な方法においては、すべての数を無限小数で表すが、それに対する方法では 9 が最後に連続することを排斥する。[53] カントール独自の議論に近いといえる証明の変形では実際に二進表現を用いており、三進表現を二進表現に変えることによりカントール集合の不可算性を同様に証明することができる。[54]
民間における文化
インターネットの登場に伴い、0.999... に関する論争は教室を抜け出し、 ニュースグループや掲示板において平凡な話題となった。その中には、通常は数学にあまり関係のないニュースグループや掲示板を多く含む。ニュースグループ sci.math においては、0.999... に関する議論は「流行のスポーツ」であり、それは FAQ で回答された問題の一つである。[55] その FAQ は 1/3 を用いる方法、10倍する方法、極限を用いる方法を簡潔に扱い、さらには同様にコーシー列にも言及している。
一般的に興味をもたれている新聞のコラム The Straight Dope の2003年版では、誤った概念に関して言及しつつ、 1/3 や極限を通して 0.999... について次のように議論している。
- 「我々の中の類人猿的要素が、『0.999... は実際に数 を表しているのではなく、過程 を表している。一つの数を見つけるために我々はその過程を途中で断ち切らなければならない。その時点において 0.999...=1 という概念は崩壊する。』と言って依然として抵抗している。
- ナンセンスだ!」[56]
The Straight Dope は「他の掲示板...ほとんどがビデオゲーム」から独立した専用の掲示板で議論を載せている。同様の調子で、0.999... の問題は、アメリカのゲーム開発会社ブリザード・エンターテイメント (Blizzard Entertainment) の Battle.net フォーラムで最初の7年間にとても一般的な話題であることがわかったため、その会社の社長 Mike Morhaime は 2004年4月1日 の記者会見で 0.999...=1 であると発表した。
- 「我々はこの問題に対しきっぱりと決着をつけることに大変興奮しています。我々は 0.999... が 1 に等しいのか等しくないのかについての、心痛や心配に立ち会ってきました。ここに次の証明を提示し、我々の顧客に対して、最終的に断固としてこの問題に対処できることを嬉しく思います。」[57]
続く Blizzard のプレスリリース(報道機関向けの発表)では、極限に基づくものと10を掛けるものの2つの証明を提供している。
関連する問題
- ゼノンのパラドックス、とりわけアキレウスと亀のパラドックスは、すぐ理解できるパラドックス 0.999...=1 を連想させる。アキレウスのパラドックスは数学的にモデル化され、0.999... と同じように等比数列を用いて解決される。しかしながら、この数学的な取り扱いがゼノンが探求していた潜在的な形而上の問題に対処しているかどうかは明らかでない。[58]
- 0 による除算 は 0.999... のいくつかの一般的な議論に見られるが、それもまた論争を引き起こす。多くの著者が 0.999... を定義することを選択する一方で、ほとんどすべての現代的な取り扱いでは 0 による除算を定義していない。というのは、それが通常の実数では意味を与えられていないからである。しかしながら、0 による除算は複素解析など他の体系では定義されている。複素解析では、拡張された複素平面(リーマン球面)は無限遠点をもつ。ここで、1/0 を無限大であると定義することには意味がある。[59]また、実際その結果は奥深く、工学や物理学に適用可能である。何人かの著名な数学者は、どの数体系も発達するずっと前からそのような定義を論じていた。[60]
- 負の 0 は数を書き表す多くの方法においては、もう1つの冗長な特徴である。実数などの数体系においては、"0" は加法に関する単位元を意味し、正の数でも負の数でもない。通常 "−0" は加法に関する 0 の逆元を表すと解釈され、−0 = 0 でなければならない。[61] それにもかかわらず、いくつかの科学的な応用では、最も共通なコンピュータの数体系(例えば 符号つき整数、1 の補数表現、IEEE 754 で定義されたような浮動小数点表示)のように、正と負の 0 を分けて用いる。[62][63] IEEE の浮動小数点数の場合は、負の 0 は、与えられた正確な数値を表すには(絶対値が)小さすぎるが、それでもなお負の数である値を表している。したがって、IEEE 浮動点数表示における「負の 0 」は真実の意味で負の "0" ではない。
注
- ^ a b cf. 同様な議論の二進数版も以下にある。 Silvanus P. Thompson, Calculus made easy, St. Martin's Press, New York, 1998. ISBN 0-312-18548-0.
- ^ Rudin p.61, Theorem 3.26; J. Stewart p.706
- ^ Euler p.170
- ^ Grattan-Guinness p.69; Bonnycastle p.177
- ^ 例えば、 J. Stewart p.706, Rudin p.61, Protter and Morrey p.213, Pugh p.180, J.B. Conway p.31
- ^ この極限については例えば以下に従う:from Rudin p. 57, Theorem 3.20e。 より直接的なアプローチについては、以下も参照: Finney, Weir, Giordano (2001) Thomas' Calculus: Early Transcendentals 10ed, Addison-Wesley, New York. Section 8.1, example 2(a), example 6(b).
- ^ Davies p.175; Smith and Harrington p.115
- ^ Beals p.22; I. Stewart p.34
- ^ Bartle and Sherbert pp.60-62; Pedrick p.29; Sohrab p.46
- ^ Apostol pp.9, 11-12; Beals p.22; Rosenlicht p.27
- ^ Apostol p.12
- ^ Bunch p.119; Tall and Schwarzenberger p.6. 最後の提案は Burrell (p.28) による。すなわち、「おそらくすべての数の中で最も安心する数は 1 であろう。したがって、0.999... を 1 として扱うときにとりわけ不安を覚える。」
- ^ Tall and Schwarzenberger pp.6-7; Tall 2000 p.221
- ^ Tall and Schwarzenberger p.6; Tall 2000 p.221
- ^ Tall 2000 p.221
- ^ Tall 1976 pp.10-14
- ^ Pinto and Tall p.5, Edwards and Ward pp.416-417
- ^ Mazur pp.137-141
- ^ Dubinsky 他 261-262
- ^ 統合の歴史的な過程は以下を参照: Griffiths and Hilton (p.xiv) in 1970。 また、再び Pugh (p.10) in 2001。 両方とも実際には公理的解析論よりもデデキンド切断を好んでいる。切断の方法の教科書については以下を参照:Pugh p.17 or Rudin p.17. 論理的視点については Pugh p.10, Rudin p.ix, or Munkres p.30
- ^ Enderton (p.113) は以下の記述を与えている。『デデキント切断の背景にあるアイディアは、有理数、つまり x より小さいすべての有理数の無限集合を与えられることによって実数 x が名づけられるということである。循環論法を避けるため、この方法で得られる有理数の集合が特徴づけられなければならない。』
- ^ Rudin pp.17-20, Richman p.399, or Enderton p.119。正確には、この3人はこの切断をそれぞれ 1*, 1−, 1R と呼んでいる。3人ともそれを伝統的な 1 の定義と同一視している。Rudin と Enderton が『実数の切断』と呼ぶものを Richman は『nonprincipal な実数の切断』と呼ぶことに注意。
- ^ Richman p.399
- ^ a b J J O'Connor and E F Robertson (2005年10月). “History topic: The real numbers: Stevin to Hilbert”. MacTutor History of Mathematics. 8月30日閲覧。accessdateの記入に不備があります。
- ^ “Mathematics Magazine:Guidelines for Authors”. The Mathematical Association of America. 8月23日閲覧。accessdateの記入に不備があります。
- ^ Richman pp.398-399
- ^ Griffiths & Hilton §24.2 "Sequences" p.386
- ^ Griffiths & Hilton pp.388, 393
- ^ Griffiths & Hilton pp.395
- ^ Griffiths & Hilton pp.viii, 395
- ^ Gowers p.60
- ^ Richman p.396; 彼の強調。この行は出版された論文の段落には見られるが、それより前に出されたプレプリントには見られない。 (訳注) reductio ad absurdum には「行き過ぎた議論」という意味もある。
- ^ Berz 439-442
- ^ John L. Bell (2003年). “An Invitation to Smooth Infinitesimal Analysis” (PDF). 6月29日閲覧。accessdateの記入に不備があります。
- ^ 非標準的な数に関する完全な取り扱いは例えば以下を参照:Robinson's Non-standard Analysis.
- ^ Lightstone pp.245-247。彼は表現の標準的な部分において、9 の繰返しの可能性を調べていない。
- ^ Berlekamp, Conway, and Guy (pp.79-80, 307-311) は 1 と 1/3 について議論されており、さらに 1/ω について触れられている。0.111... のゲームはバールカンプのルールに直接にしたがっており、それは以下に述べられている。A. N. Walker (1999年). “Hackenstrings and the 0.999… =1 FAQ”. 6月29日閲覧。accessdateの記入に不備があります。
- ^ Richman pp.397-399
- ^ Richman pp.398-400. Rudin (p.23) は第1章の最後の練習問題として、この代替構造(ただし実数上)を選んでいる。
- ^ Gardiner p.98; Gowers p.60
- ^ a b Fjelstad p.11
- ^ Fjelstad pp.14-15
- ^ DeSua p.901
- ^ DeSua pp.902-903
- ^ Petkovšek p.408
- ^ Protter and Morrey p.503; Bartle and Sherbert p.61
- ^ Komornik and Loreti p.636
- ^ Kempner p.611; Petkovšek p.409
- ^ Petkovšek pp.410-411
- ^ Leavitt 1984 p.301
- ^ Lewittes pp.1-3; Leavitt 1967 pp.669,673; Shrader-Frechette pp.96-98
- ^ Pugh p.97; Alligood, Sauer, and Yorke pp.150-152。Protter と Morrey (p.507) および Pedrick (p.29) はこの記述を練習問題として位置づけている。
- ^ マオール (Maor) (p.60) およびマンキェヴィチ (Mankiewicz) (p.151) は前者の方法を振り返る。マンキェヴィチはそれがカントールの仕事だとしているが、最初の出所は定かではない。Munkres (p.50) は後者の方法に言及している。
- ^ Rudin p.50, Pugh p.98
- ^ Richman (p.396)が述べている。 Hans de Vreught (1994年). “sci.math FAQ: Why is 0.9999… = 1?”. 6月29日閲覧。accessdateの記入に不備があります。
- ^ Cecil Adams (2003年7月11日). “An infinite question: Why doesn't .999~ = 1?”. The Straight Dope. The Chicago Reader. 9月6日閲覧。accessdateの記入に不備があります。
- ^ “Blizzard Entertainment® Announces .999~ (Repeating) = 1”. Press Release. Blizzard Entertainment (2004年4月1日). 9月3日閲覧。accessdateの記入に不備があります。
- ^ Wallace p.51, Maor p.17
- ^ 例えば以下を参照。 J.B. Conway's treatment of Möbius transformations, pp.47-57
- ^ Maor p.54
- ^ Munkres p.34, Exercise 1(c)
- ^ Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2e ed.). W. H. Freeman. pp. 462. ISBN 0-7167-1088-9
- ^ “Floating point types”. MSDN C# Language Specification. 8月29日閲覧。accessdateの記入に不備があります。
参考文献
- Alligood, Sauer, and Yorke (1996). “4.1 Cantor Sets”. Chaos: An introduction to dynamical systems. Springer. ISBN 0-387-94677-2
- 力学に関するこの入門的な教科書は、学部生または初級の大学院生向けである。(p.ix)
- Apostol, Tom M. (1974). Mathematical analysis (2e ed.). Addison-Wesley. ISBN 0-201-00288-4
- 微積分学からより進んだ解析学 Mathematical analysis への変遷が「ごまかさないで、厳密で、最新であると同時に学者ぶることのないように」意図されている。(序文)Apostol は実数の構成に上限の存在公理を用いており、無限小数が2ページ後で紹介されている。(pp.9-11)
- Bartle, R.G. and D.R. Sherbert (1982). Introduction to real analysis. Wiley. ISBN 0-471-05944-7
- このテキストは「実解析の基本的性質と技巧を扱う、理解しやすくてほどよい進度の教科書」を目指している。実数の構成には上限の存在公理を用いている。(pp.vii-viii)
- Beals, Richard (2004). Analysis. Cambridge UP. ISBN 0-521-60047-2
- Berlekamp, E.R.; J.H. Conway; and R.K. Guy (1982). Winning Ways for your Mathematical Plays. Academic Press. ISBN 0-12-091101-9
- Berz, Martin (1992). “Automatic differentiation as nonarchimedean analysis”. Computer Arithmetic and Enclosure Methods (Elsevier): 439-450.
- Bunch, Bryan H. (1982). Mathematical fallacies and paradoxes. Van Nostrand Reinhold. ISBN 0-442-24905-5
- この本は、その中心的な話題「数学的な現実性と物理的な現実性のやや希薄な関係」を調べる道具として、パラドックスと誤った推論による解析を紹介している。高校1年生程度の代数を仮定しており、(第2章の等比数列を含めて)さらに進んだ数学はこの本の中で発展していく。 0.999... は完全に扱われているものの一つではないが、カントールの対角線論法を扱うなかで簡潔に述べられている。(pp.ix-xi, 119)
- Burrell, Brian (1998). Merriam-Webster's Guide to Everyday Math: A Home and Business Reference. Merriam-Webster. ISBN 0-87779-621-1
- Conway, John B. (1978) [1973]. Functions of one complex variable I (2e ed.). Springer-Verlag. ISBN 0-387-90328-3
- このテキストは必修科目としての「基本的な微積分の厳密な課程」の役割を担っており、述べられているその原則は "An Introduction to Mathematics" として複素解析を紹介し、対象を明確に正確に述べることである。(p.vii)
- Davies, Charles (1846). The University Arithmetic: Embracing the Science of Numbers, and Their Numerous Applications. A.S. Barnes
- DeSua, Frank C. (November 1960). “A system isomorphic to the reals” (restricted access). The American Mathematical Monthly 67 (9): 900-903.
- Dubinsky, Ed, Kirk Weller, Michael McDonald, and Anne Brown (2005). “Some historical issues and paradoxes regarding the concept of infinity: an APOS analysis: part 2”. Educational Studies in Mathematics 60: 253-266. doi:10.1007/s10649-005-0473-0.
- Edwards, Barbara and Michael Ward (May 2004). “Surprises from mathematics education research: Student (mis)use of mathematical definitions”. The American Mathematical Monthly 111 (5): 411-425.
- Enderton, Herbert B. (1977). Elements of set theory. Elsevier. ISBN 0-12-238440-7
- 集合論の入門的な学部生用の教科書であり、「特別な予備知識を前提としない」。公理的集合論または数体系の構成に焦点をおいた学習課程を提供するために書かれているが、公理という題材は、あまり重要視されないような方法で扱われている。(pp.xi-xii)
- Euler, Leonhard (1822) [1770]. John Hewlett and Francis Horner, English translators.. ed. Elements of Algebra (3rd English edition ed.). Orme Longman
- Fjelstad, Paul (January 1995). “The repeating integer paradox” (restricted access). The College Mathematics Journal 26 (1): 11-15. doi:10.2307/2687285.
- Gardiner, Anthony (2003) [1982]. Understanding Infinity: The Mathematics of Infinite Processes. Dover. ISBN 0-486-42538-X
- Gowers, Timothy (2002). Mathematics: A Very Short Introduction. Oxford UP. ISBN 0-19-285361-9
- Grattan-Guinness, Ivor (1970). The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press. ISBN 0-262-07034-0
- Griffiths, H.B.; P.J. Hilton (1970). A Comprehensive Textbook of Classical Mathematics: A Contemporary Interpretation. London: Van Nostrand Reinhold. ISBN 0-442-02863-6. (LCC QA37.2 G75)
- この本は、バーミンガム地方のグラマースクールの数学教師の課程から生まれたものである。この課程は、学校で教えられる数学をもとにして大学レベルの数学への展望を伝えるのが目的であり、「大学で数学の専門課程を1年間学んだ程度のレベル」の生徒向けである。実数の構成は第24章で述べられているが、「おそらくこの本全体の中で最も難しい章」である。しかしながら著者たちはこの難しさをイデアル論を用いているためとしている。イデアル論はここでは扱われていない。(pp.vii, xiv)
- Kempner, A.J. (December 1936). “Anormal Systems of Numeration” (restricted access). The American Mathematical Monthly 43 (10): 610-617.
- Komornik, Vilmos; and Paola Loreti (1998). “Unique Developments in Non-Integer Bases” (restricted access). The American Mathematical Monthly 105 (7): 636-639.
- Leavitt, W.G. (1967). “A Theorem on Repeating Decimals” (restricted access). The American Mathematical Monthly 74 (6): 669-673.
- Leavitt, W.G. (September 1984). “Repeating Decimals” (restricted access). The College Mathematics Journal 15 (4): 299-308.
- Lewittes, Joseph (2006年). “Midy's Theorem for Periodic Decimals”. New York Number Theory Workshop on Combinatorial and Additive Number Theory. arXiv. Template:Cite webの呼び出しエラー:引数 accessdate は必須です。
- Lightstone, A.H. (March 1972). “Infinitesimals” (restricted access). The American Mathematical Monthly 79 (3): 242-251.
- Mankiewicz, Richard (2000). The story of mathematics. Cassell. ISBN 0-304-35473-2
- Mankiewicz は、数学、数学者の著作、歴史的概略の視覚的な側面と質的な側面を組み合わせることによって『理解しやすい形式で数学の歴史』を述べようとしている。(p.8)
- Maor, Eli (1987). To infinity and beyond: a cultural history of the infinite. Birkhäuser. ISBN 3-7643-3325-1
- 年代順というより話題別の無限に関する回顧。この本は「一般的な読者を意図している」が「数学者の視点から語っている」。数学的な厳密性と読みやすい言葉遣いの板ばさみで、Maor は「この問題を正しく取り扱うことに成功したことを願っている」と述べている。(pp.x-xiii)
- Mazur, Joseph (2005). Euclid in the Rainforest: Discovering Universal Truths in Logic and Math. Pearson: Pi Press. ISBN 0-13-147994-6
- Munkres, James R. (2000) [1975]. Topology (2e ed.). Prentice-Hall. ISBN 0-13-181629-2
- 形式的な予備知識を必要としないで「大学3~4年生または大学院の1年生レベル」における入門書を意図している。「読者が集合論についてよく知っていることを仮定すらしない。」(p.xi) Munkres の実数の扱いは公理的であり、この道具を持たない構成方法について彼は「このアプローチの方法は多くの時間と努力を必要とし、数学的な興味として扱うよりもはるかに論理的である。」と述べている。(p.30)
- Pedrick, George (1994). A First Course in Analysis. Springer. ISBN 0-387-94108-8
- Petkovšek, Marko (May 1990). “Ambiguous Numbers are Dense” (restricted access). American Mathematical Monthly 97 (5): 408-411.
- Pinto, Márcia and David Tall (2001). “Following students' development in a traditional university analysis course”. PME25: v4: 57-64.
- Protter, M.H. and C.B. Morrey (1991). A first course in real analysis (2e ed.). Springer. ISBN 0-387-97437-7
- この本は「微積分学の標準的な仮定を終えた生徒に適切な、解析学の理論的構成を紹介する」ことを目標とする。(p.vii) 第2章の終わりで著者は、実数において有界単調列が収束するということを公理として仮定しているが、その後で区間縮小法の原理と上限の存在の性質を証明している。(pp.56-64) 小数展開は Appendix 3 "Expansions of real numbers in any base" に見られる。(pp.503-507)
- Pugh, Charles Chapman (2001). Real mathematical analysis. Springer-Verlag. ISBN 0-387-95297-7
- 実数のよく知られた性質を仮定する一方で、Pugh はできるだけ早い段階で実数の切断を紹介する。公理的な取り扱いについて「実数の体系に基づいて実数が構成されていることを考えると、これは一つの詐欺である。」と述べている。(p.10) 上限の存在の性質とそれに関係するいくつかの事実を証明した後は、その他の場面で切断は用いられていない。
- Richman, Fred (December 1999). “Is 0.999… = 1?” (restricted access). Mathematics Magazine 72 (5): 396-400. Free HTML preprint: Richman, Fred (1999年6月8日). “Is 0.999… = 1?”. 8月23日閲覧。accessdateの記入に不備があります。 注:雑誌の論文にはプレプリントには見られない記述が含まれている。
- Robinson, Abraham (1996). Non-standard analysis (Revised edition ed.). Princeton University Press. ISBN 0-691-04490-2
- Rosenlicht, Maxwell (1985). Introduction to Analysis. Dover. ISBN 0-486-65038-3
- Rudin, Walter (1976) [1953]. Principles of mathematical analysis (3e ed.). McGraw-Hill. ISBN 0-07-054235-X
- より進んだ学部生の課程のための教科書。「有理数から実数を構成する方法からはじめるのは(論理的には正しいけれども)教育上好ましくないことを経験上確信している。初期の段階では、多くの生徒は、このことの必要性についてその価値を認めることができない。それゆえ、実数の体系は、上限が存在する実数体として紹介され、この性質の興味深いいくつかの応用例がすぐになされる。デデキントの構成は無視されている。現在はこれは第1章の Appendix にあり、機が熟したときにいつでも勉強して楽しむことができる。」(p.ix)
- Shrader-Frechette, Maurice (March 1978). “Complementary Rational Numbers” (restricted access). Mathematics Magazine 51 (2): 90-98.
- Smith, Charles and Charles Harrington (1895). Arithmetic for Schools. Macmillan
- Sohrab, Houshang (2003). Basic Real Analysis. Birkhäuser. ISBN 0-8176-4211-0
- Stewart, Ian (1977). The Foundations of Mathematics. Oxford UP. ISBN 0-19-853165-6
- Stewart, James (1999). Calculus: Early transcendentals (4e ed.). Brooks/Cole. ISBN 0-534-36298-2
- この本は「生徒たちが微積分を理解するのを援助」し、「観念に対する理解を育成する」ことを目的としている。(p.v) 微積分の基本性質の証明は省略されている。
- D.O. Tall and R.L.E. Schwarzenberger (1978). “Conflicts in the Learning of Real Numbers and Limits”. Mathematics Teaching 82: 44-49.
- Tall, David (1976/7). “Conflicts and Catastrophes in the Learning of Mathematics”. Mathematical Education for Teaching 2 (4): 2-18.
- Tall, David (2000). “Cognitive Development In Advanced Mathematics Using Technology”. Mathematics Education Research Journal 12 (3): 210-230.
- von Mangoldt, Dr. Hans (1911). “Reihenzahlen” (German). Einführung in die höhere Mathematik (1st ed. ed.). Leipzig: Verlag von S. Hirzel
- Wallace, David Foster (2003). Everything and more: a compact history of infinity. Norton. ISBN 0-393-00338-8














