リミットサイクル

ファン・デル・ポール振動子で現れる安定なリミットサイクル。内側の軌道も外側の軌道も、ある閉軌道に漸近している。

リミットサイクル（英: limit cycle, 仏: cycle limite）とは、力学系における相空間上での閉軌道であり、時間 t を無限大、またはマイナス無限大にしたとき、その閉軌道に収束する軌道が少なくとも1つ存在するものである。極限閉軌道や極限周期軌道とも呼ばれる。1881年、力学系の始祖でもあるアンリ・ポアンカレによって初めて見いだされた。

リミットサイクルは非線形系でのみ現れる。リミットサイクルと充分に近い軌道が、全てリミットサイクルに収束するとき、漸近安定である、または単に安定であるという。

安定なリミットサイクルでは、相空間上の様々な初期値から出発した軌道は閉軌道に収束する。閉軌道に小さな摂動が加わっても元の閉軌道に戻る。物理的には、リミットサイクルは自励振動の数理モデルとなる。リミットサイクルを持つ例として、ファン・デル・ポール振動子がある。代数的微分方程式におけるリミットサイクル軌道の数を求める問題は、ヒルベルトの第16問題の第2の問題として知られる。2次元相空間の場合は、ポアンカレ・ベンディクソンの定理などによってリミットサイクルの存在（または非存在）を予見できる。

定義

系の時間を t ∈ R、状態変数を X = (x₁, x₂, ... , x_n) ∈ Rⁿ とする。n 次元連続力学系のある解 X(t) が平衡解ではなく、なおかつ X(t) = X(t + T) を満たすような T > 0 が存在するとき、X(t) は周期解と呼ばれる。特に X(t) = X(t + T) を満たす最小の T は周期と呼ばれる。 時間 t が ∞ から −∞ まで変わるときに解 X(t) が取る像の集まりを軌道と呼ぶ。軌道は、系の相空間 x₁, x₂, ... , x_n 上に描かれる一つの曲線に対応する。周期解が描く軌道は、閉軌道や周期軌道と呼ばれる。閉軌道を C で表すとする。相空間 x₁, x₂, ... , x_n 上で C は単純閉曲線となる。

リミットサイクルは次のように定義される。ある初期値 X₀ = X(0) が与えられt解を ϕ (t, X₀) と表すとする。相空間上にある閉軌道 C が存在するとする。C のある近傍 U が存在し、U 上の任意の点を初期値とする ϕ (t, X₀) が t → ∞ または t → −∞ で C に漸近するとき、C はリミットサイクルと呼ばれる。言い換えると、d(ϕ(t, X₀), C) を点 ϕ (t, X₀) と集合 C の内の ϕ (t, X₀) に最も近い点のあいだの距離として定義するとき、

$\lim _{t\to \infty }d(\phi (t,X_{0}),C)=0$

または

$\lim _{t\to -\infty }d(\phi (t,X_{0}),C)=0$

となる C と X₀ ∉ C が存在するとき、C はリミットサイクルと呼ばれる。

リミットサイクル型の振動を示す系をリミットサイクル振動子などとも呼ぶ。「リミット」は極限集合を意味し、リミットサイクルは極限閉軌道、極限周期軌道、極限サイクルなどとも呼ばれる。極限集合とは軌道が収束する先を意味し、とくに収束先が1点である場合だけでなく閉軌道のような例も含めて定義したものである。

極限集合には t → ∞ 方向の ω 極限集合と t → −∞ 方向の α 極限集合の2つがある。極限集合を用いてリミットサイクルを定義すると次のようになる。ある初期値 X₀ の軌道は閉軌道ではないとする。しかし、その初期値 X₀ の ω 極限集合 ω(X₀) または α 極限集合 α(X₀) が閉軌道だとする。このとき、ω(X₀) または α(X₀) はリミットサイクルと呼ばれる。

2次元連続力学系では、相平面上でリミットサイクルは必ず孤立した閉軌道となる。すなわち、リミットサイクルとなる閉軌道 C の近傍には他の閉軌道は存在し得ない。近傍内の全ての軌道は、C に吸引されるように近づくか、C から反発するように遠ざかるかの2通りしかない。相空間上の「孤立した閉軌道」をリミットサイクルの定義とする流儀もある。

周りの軌道を吸引するリミットサイクルは漸近安定あるいは単に安定であるという。安定なリミットサイクルはアトラクタの1種である。リアプノフ指数で特徴付けすると、閉軌道接線方向のリアプノフ指数は 0 で、その他の方向のリアプノフ指数は負であるのが安定なリミットサイクルである。安定なリミットサイクルのことを周期アトラクタともいう。

周りの軌道を反発するリミットサイクルは軌道不安定あるいは単に不安定であるという。相平面のリミットサイクルで、内側の軌道が吸引されて外側の軌道が反発するような場合、あるいは内側の軌道が反発して外側の軌道が吸引されるような場合、これらの場合のリミットサイクルは半安定であるという。

存在条件

実数直線 R 上の1次元自律系の微分方程式系では、周期解は存在し得ない。2次元自律系あるいは1次元非自律系以上から周期解が現れるようになる。また、リミットサイクルは非線形の系のみで起こる現象である。線形の系ではリミットサイクルは起こらない。

流れに沿って相空間の体積が変化しない系を保存系と呼び、体積が零に漸近する系を散逸系と呼ぶ。散逸系の場合にリミットサイクルが存在する。周期軌道が散逸系で存在する場合、それらの周期軌道の大抵はリミットサイクルであると推定される。系が勾配系である場合も、リミットサイクルは存在しない。

以下、変数の時間微分 d/dt を変数の上部に · を付けて表す（ニュートンの記法）。もし、系を2次元自律系

${\begin{aligned}{\dot {x}}&=f(x,\ y),\\{\dot {y}}&=g(x,\ y)\end{aligned}}$

に限定すれば、閉軌道およびリミットサイクルの有無が判別できる定理がいくつかある。ポアンカレ・ベンディクソンの定理により、平衡点を含まない有界な軌道の極限集合は閉軌道である。すなわち、このような軌道は閉軌道そのものか、存在するリミットサイクルに吸引される軌道であるかのどちらかである。さらに、ベンディクソンの条件によれば、単連結な領域 Ω 上で

$\operatorname {div} (f(x,\ y),\ g(x,\ y))={\frac {\partial f(x,\ y)}{\partial x}}+{\frac {\partial g(x,\ y)}{\partial y}}$

の値が零ではなく、かつ符号が一定であれば、Ω に完全に含まれる閉軌道は存在しない。また、系がリエナール方程式に相当するのであれば、リエナールの定理により原点を囲む漸近安定なリミットサイクルが存在する。

力学系のパラメータ（定数係数）が変化することによって、解に定性的な変化が起こることを分岐という。リミットサイクルも分岐を経て発生する。2次元系でリミットサイクルが発生する典型的な分岐は、ホップ分岐と呼ばれる分岐である。ホップ分岐では、パラメータ変化によって安定な平衡点が不安定に遷移し、その周囲に安定なリミットサイクルが起こる。あるいは、安定な平衡点と不安定なリミットサイクルが不安定な平衡点に遷移する場合もある。ホップ分岐は局所分岐の1種である。リミットサイクルが関わる大域分岐としては、ホモクリニック分岐やリミットサイクル同士が衝突するサドルノード分岐などがある。

2次元系のリミットサイクルにポアンカレ写像を適用した図。局所断面上の状態点が不動点へ漸近していく様子を示す。

周期軌道の安定性は、ポアンカレ写像の構成や周期軌道周りの線形化方程式（変分方程式）の構成から判別できる。適当な n − 1 次元の局所断面を取り、ポアンカレ写像を設定することで連続力学系の周期解を離散力学系の写像に置き換えることができる。写像が漸近安定な不動点を持つ場合は元の周期軌道が漸近安定である。ポアンカレ写像は、リミットサイクルを見出したポアンカレ自身がリミットサイクルを考察するために生み出した手法である。あるいは、周期軌道からの微小なズレを想定して周期軌道に対する線形化方程式を構成することによって、フロケ理論を適用することができる。線形化方程式のフロケ乗数あるいはフロケ指数から周期軌道の安定性が決定できる。ただし、ポアンカレ写像による方法も線形化方程式による方法も、任意の微分方程式系に適用できる解析的な一般的手法は存在しない。ポアンカレ写像であれば対象の系ごとに個別に工夫して構成する必要があり、フロケ乗数による判定であれば数値計算による手法がある。

具体例

2次元系

微分方程式系 ${\dot {x}}=x-y-x(x^{2}+y^{2})$, ${\dot {y}}=x+y-y(x^{2}+y^{2})$ の方向場。原点を除く全ての軌道は回転しながら単位円の閉軌道に漸近する。

リミットサイクルが現れる簡単な微分方程式系の例として、

${\begin{aligned}{\dot {x}}&=x-y-x(x^{2}+y^{2}),\\{\dot {y}}&=x+y-y(x^{2}+y^{2})\end{aligned}}$

という2次元系がある。この系を極座標で表せば、

${\begin{aligned}{\dot {r}}&=r(1-r^{2}),\\{\dot {\theta }}&=1\end{aligned}}$

となり、動径 r と偏角 θ の振る舞いが互いに無関係に決まる単純な形となる。θ(t) の一般解は一定振動数で回転し続ける関数となる。r(t) の一般解は

$r(t)={\frac {r_{0}}{\sqrt {r_{0}^{2}+(1-r_{0}^{2})e^{-2t}}}}$

という関数となる。ここで、r₀ は t = 0 における r の値である。よって、r₀ ≠ 0 であれば、r(t) は t → ∞ で r → 1 であり、系の原点を除く全ての軌道は回転しながら単位円に近づいていくこととなる。この結果は、明示的な一般解を必要としない簡易な安定判別によっても得られる。よって、原点を中心とする単位円がこの系の安定なリミットサイクルである。

上記の微分方程式系にパラメータ a を与えた

${\begin{aligned}{\dot {r}}&=r(a-r^{2}),\\{\dot {\theta }}&=1\end{aligned}}$

では、a > 0 であれば、半径 √a の円が上記と同様に安定なリミットサイクルである。しかし a < 0 のときは、全ての軌道は原点に収束する。a = 0 のときも、代数的なオーダーの速さだが全ての軌道は原点に収束する。a > 0 になったときに、原点は不安定となり、原点周囲に安定なリミットサイクルが発生する。よって、この系では a = 0 でホップ分岐が起きている。

ファン・デル・ポール方程式における、それぞれのリミットサイクルに漸近する軌道の様子。

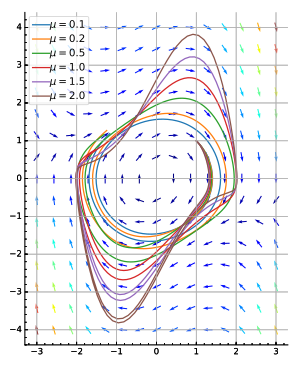
上記は解析解を得ることができる例だが、ほとんどの非線形微分方程式系は解析的に解くことはできない。非線形振動現象の代表的な例であり、なおかつ実際の現象に由来する二階非線形微分方程式として、バルタザール・ファン・デル・ポールが三極真空管の発振回路で起こる自励振動を解明するために導いたファン・デル・ポール方程式がある。2次元微分方程式系の形では、ファン・デル・ポール方程式は

${\begin{aligned}{\dot {x}}&=y,\\{\dot {y}}&=\mu (1-x^{2})y-x\end{aligned}}$

として表される。ここで μ > 0 がパラメータである。

上記の例と異なり、このファン・デル・ポール方程式の解は初等関数で表すことができない。しかし上記の例と同様に、原点周りにリミットサイクルが存在し、初期値が原点を取る場合を除いて全ての軌道がリミットサイクルに収束する。この証明はポアンカレ写像を構成する手法で行うことができる。あるいは、ファン・デル・ポール方程式はリエナール方程式の1種であることから、リエナールの定理よりファン・デル・ポール方程式系の相平面上には唯一の安定なリミットサイクルが存在することがわかる。

ファン・デル・ポール方程式のリミットサイクルは μ の値によってその形状が変化する。μ が小さいほど、リミットサイクルは円軌道に近づく。μ が大きいほど形状は円から離れていき、μ が大きいほど第1象限と第3象限で背が高くなる。このとき、時系列では弛張振動の様相を示し、緩やかな変化と急な変化の組み合わせから成る振動現象が起きている。

3次元系

1周期 (a = 0.1, b = 0.1, c = 4)

2周期 (a = 0.1, b = 0.1, c = 6)

4周期 (a = 0.1, b = 0.1, c = 8.5)

レスラー方程式のリミットサイクル。a = b = 0.1 で固定して、c を変えたとき。

3次元系においてリミットサイクルが現れる微分方程式系としては、レスラー方程式やローレンツ方程式などがある。オットー・レスラーが提案したレスラー方程式は

${\begin{aligned}{\dot {x}}&=-y-z,\\{\dot {y}}&=x+ay,\\{\dot {z}}&=b+xz-cz\end{aligned}}$

で表される微分方程式系で、a, b, c がパラメータである。非線形項は第3式の xz のみであるにも拘らず、レスラー方程式の解は様々な振る舞いを見せる。

例えば、a = 0.1, b = 0.1, c = 4 というパラメータ値の組み合わせで、レスラー方程式の相空間には安定なリミットサイクルが現れる。ここから、a と b の値は 0.1 のままとして c の値を増やしていくと、ある c の値で1重巻きの閉曲線であったリミットサイクルは2重巻きの閉曲線に移り変わる。すなわち、2周して元の状態に戻るような閉曲線になる。パラメータ c の変化によって周期 T の長さがおおよそ倍になる分岐が起きており、このような分岐を周期倍分岐と呼ぶ。リミットサイクルが2重巻きになるには、閉軌道が交差せずに2周できる空間の余地が必要となる。よって、このようなリミットサイクルの周期倍分岐は3次元以上の系でのみ起こる現象である。

周期倍分岐を経て、例えば a = 0.1, b = 0.1, c = 6 のとき、レスラー方程式のリミットサイクルは2重巻き（2周期）の状態にある。さらに c の値を増やしていくと2重巻きのリミットサイクルは4重巻きのリミットサイクルになり、周期はさらに倍になる。以下同様に、c の値の増加に伴って周期倍分岐が起き続け、ある c の値で周期は無限となり、リミットサイクルからカオスへ変わる。これは系のアトラクタがカオス（ストレンジアトラクタ）へと分岐するルートの一つで、周期倍分岐ルートと呼ばれる。この例では、 a = 0.1, b = 0.1, c = 9 のアトラクタはカオスである。

レスラー方程式は、エドワード・ローレンツが提案したローレンツ方程式に触発され、導入されたものであった。ローレンツ方程式でもまた同様に、リミットサイクルの存在と周期倍分岐ルートが確認される。また、チュア回路では、2つのリミットサイクルが同時に存在する様とそれぞれの周期倍分岐が見られる。

実存の現象

実存する現象に対して、リミットサイクルは自励振動現象の数理モデルとなり得る。自励振動とは、流入するエネルギーは非振動的であるにも拘らず、系自身の特性から自ずと発生する振動現象である。リミットサイクル振動子には、外力による強制振動の周期に依存せずに系自身でリズムを生み出す自律性がある。また、リミットサイクル振動子に外乱が加わった場合、一時的に振幅が変化するかもしれないが、外乱が無くなれば元の振幅に戻ることができる。このようなリミットサイクルの安定性は、工学的にも生物的にも重要である。

初期状態に依存せずに安定なリズムを作るメトロノーム

一定のリズムを鳴らす機械式のメトロノームは安定なリズムの好例である。最初に針を小さく振って動かしたとしても、針を大きく振って動かしたとしても、メトロノームは一定の振動に落ち着く。メトロノームの減衰力と駆動力がバランスすることによって安定な振動を生み出しており、簡単なモデル化によってもメトロノームにおけるリミットサイクルの存在が確認できる。また例えば心臓の拍動などのように、生物のリズム現象の多くは（生物分野では恒常性と呼ばれる）安定性を持っている。このような安定なリズムを記述するのにリミットサイクルを持つモデルが有効である。

参照文献

• Steven H. Strogatz、田中 久陽・中尾 裕也・千葉 逸人（訳）、2015、『ストロガッツ　非線形ダイナミクスとカオス ―数学的基礎から物理・生物・化学・工学への応用まで―』、丸善出版 ISBN 978-4-621-08580-6
• 郡 宏・森田 善久、2011、『生物リズムと力学系』初版、共立出版〈シリーズ・現象を解明する数学〉 ISBN 978-4-320-11000-7
• 桑村 雅隆、2015、『パターン形成と分岐理論 ―自発的パターン発生の力学系入門―』初版、共立出版〈シリーズ・現象を解明する数学〉 ISBN 978-4-320-11004-5
• 船越 満明、2008、『カオス』初版、朝倉書店〈シリーズ 非線形科学入門3〉 ISBN 978-4-254-11613-7
• Morris W. Hirsch; Stephen Smale; Robert L. Devaney、桐木 紳・三波 篤朗・谷川 清隆・辻井 正人（訳）、2007、『力学系入門　原著第2版 ―微分方程式からカオスまで―』初版、共立出版 ISBN 978-4-320-01847-1
• 上田 睆亮、2008、『カオス現象論』初版、コロナ社〈現代非線形科学シリーズ12〉 ISBN 978-4-339-02611-5
• K.T.アリグッド・T.D.サウアー・J.A.ヨーク、津田 一郎（監訳）、星野 高志・阿部 巨仁・黒田 拓・松本 和宏（訳）、2012b、『カオス　第2巻　力学系入門』、丸善出版 ISBN 978-4-621-06279-1
• S. ウィギンス、丹羽 敏雄（監訳）、今井 桂子・田中 茂・水谷 正大・森 真（訳）、2013、『非線形の力学系とカオス』新装版、丸善出版 ISBN 978-4-621-06435-1
• 香田 徹・小室 元政・松本 隆・CHUA, Leon O.・徳永 隆治・相沢 洋二・大石 真一・八幡 英雄、合原 一幸（編）、1990、『カオス ―カオス理論の基礎と応用―』初版、サイエンス社 ISBN 4-7819-0592-7
• 川上 博 (2005年). “非線形現象入門”. 徳島大学 教育・研究者情報データベース. 2018年6月14日閲覧。
• “1群11編 非線形問題 1章 非線形力学系”. 電子情報通信学会知識ベース. pp. 1–13 (2010年9月16日). 2018年6月16日閲覧。

外部リンク

• 「リミットサイクル」 - 日本天文学会 編『天文学辞典』
• Limit cycle - Encyclopedia of Mathematics
• リミットサイクル - J-GLOBAL
• Chaos4 Japanese（カオス4 ブランコ） - YouTube　力学系、バタフライ効果、カオス理論に関する一般向けビデオ「CHAOS」、第4章、日本語訳：坪井俊