「マンハッタン距離」の版間の差分
編集の要約なし |
IAmKungLao (会話 | 投稿記録) ページ「Taxicab geometry」の翻訳により作成 タグ: サイズの大幅な増減 コンテンツ翻訳 コンテンツ翻訳バージョン2 |
||
| 1行目: | 1行目: | ||
[[ファイル:Manhattan_distance.svg|サムネイル|200x200ピクセル| マンハッタン距離とユークリッド距離の比較:マンハッタン距離では、赤、黄、青のパスの最短パス長はすべて同じ12である。 ユークリッド幾何学では、緑の線は長さを持っている<math>6 \sqrt{2} \approx 8.49</math>ユニークな最短経路である。 ]] |
|||
[[Image:Manhattan distance bgiu.png|thumb|250px|right|マンハッタン距離の例: どの色のコースを辿っても同じ距離が決まっている]] |
|||
'''マンハッタン距離'''(マンハッタンきょり、''Manhattan distance'')または'''''L''<sub>1</sub>-距離'''は、[[幾何学]]における[[距離空間|距離概念]]のひとつ。各座標の差(の[[絶対値]])の総和を2点間の距離とする。 |
'''マンハッタン距離'''(マンハッタンきょり、''Manhattan distance'')または'''''L''<sub>1</sub>-距離、タクシーの幾何、 直線距離 、 ''L'' <sub>1</sub>距離 、 ''L'' <sup>1</sup>距離、<math>\ell_1</math>ノルム ( [[Lp空間|''L'' <sup>''p''</sup> spaceを]]参照)、 [[ヘビゲーム|スネーク]]距離 、 シティブロック距離'''は、[[幾何学]]における[[距離空間|距離概念]]のひとつ。各座標の差(の[[絶対値]])の総和を2点間の距離とする。 |
||
[[ユークリッド幾何学]]における[[ユークリッド計量|通常の距離]]([[ユークリッド距離]])に代わり、この距離概念を用いた幾何学は'''タクシーの幾何''' (''taxicab geometry'') と呼ばれる。[[19世紀]]に[[ヘルマン・ミンコフスキー]]によって考案された。 |
[[ユークリッド幾何学]]における[[ユークリッド計量|通常の距離]]([[ユークリッド距離]])に代わり、この距離概念を用いた幾何学は'''タクシーの幾何''' (''taxicab geometry'') と呼ばれる。[[19世紀]]に[[ヘルマン・ミンコフスキー]]によって考案された。 |
||
通常の距離関数または[[ユークリッド幾何学]]の[[距離函数|メトリック]]が、2点間の[[距離]]が[[直交座標系|デカルト座標]]の[[絶対差]]の合計である新しいメトリックで置き換えられる幾何学の形式である。 。 <ref>{{Cite web|url=https://xlinux.nist.gov/dads/HTML/manhattanDistance.html|title=Manhattan distance|first=Paul E.|author=Black|website=Dictionary of Algorithms and Data Structures|accessdate=October 6, 2019}}</ref> '''マンハッタン距離'''の名前は、 [[マンハッタン]]島の[[1811年委員会計画|ほとんどの道路のグリッドレイアウト]]を暗示している 。これにより、車が[[行政区 (ニューヨーク市)|自治区内]]の2つの交差点間を移動できる最短距離は、タクシージオメトリの交差点の距離と同じになる。 |
|||
| ⚫ | |||
| ⚫ | |||
ジオメトリは18世紀から[[回帰分析]]で使用されており、今日ではしばしば[[ラッソ回帰|LASSO]]と呼ばれている。 幾何学的解釈は、19世紀の[[非ユークリッド幾何学]]にさかのぼり、 [[ヘルマン・ミンコフスキー|ヘルマンミンコフスキー]]によるものである。 |
|||
| ⚫ | |||
| ⚫ | |||
タクシー距離、 <math>d_1</math> 、2つのベクトル間<math>\mathbf{p}, \mathbf{q}</math> [[直交座標系|デカルト座標系]]が固定された''n''次元の[[実数]] [[ベクトル空間]]では、 [[直交座標系|座標軸]]への点間の[[線分|線分の]]投影の長さの合計である。 より正式には、 |
|||
: <math>d_1(\mathbf{p}, \mathbf{q}) = \|\mathbf{p} - \mathbf{q}\|_1 = \sum_{i=1}^n |p_i-q_i|,</math> |
|||
<math>(\mathbf{p}, \mathbf{q})</math>は [[空間ベクトル|ベクトル]]である。 |
|||
: <math>\mathbf{p}=(p_1,p_2,\dots,p_n)\text{ and }\mathbf{q}=(q_1,q_2,\dots,q_n)\,</math> |
|||
たとえば、 [[平面|飛行機]]では、タクシーの距離<math>(p_1,p_2)</math>そして<math>(q_1,q_2)</math>である<math>| p_1 - q_1 | + | p_2 - q_2 |.</math> |
|||
| ⚫ | |||
| ⚫ | |||
ただし、<math>\boldsymbol{x} := (x_1, x_2, ..., x_n)</math>, <math>\boldsymbol{y} := (y_1, y_2, ..., y_n)</math> とおいた。例えば、[[平面]]上において座標 <math>(x_1, y_1)</math> に置かれた点 <math>P_1</math> と、座標 <math>(x_2, y_2)</math> に置かれた点 <math>P_2</math> 間のマンハッタン距離は |
ただし、<math>\boldsymbol{x} := (x_1, x_2, ..., x_n)</math>, <math>\boldsymbol{y} := (y_1, y_2, ..., y_n)</math> とおいた。例えば、[[平面]]上において座標 <math>(x_1, y_1)</math> に置かれた点 <math>P_1</math> と、座標 <math>(x_2, y_2)</math> に置かれた点 <math>P_2</math> 間のマンハッタン距離は |
||
:<math>|x_1 - x_2| + |y_1 - y_2|</math> |
: <math>|x_1 - x_2| + |y_1 - y_2|</math> |
||
となる。 |
となる。 |
||
== プロパティ == |
|||
タクシー距離は、座標系の[[回転]]に依存するが、座標軸に関するその[[鏡映|反射]]またはその[[平行移動|並進に]]は依存しない。 全てのマンハッタン距離を満たすヒルベルトの公理 (の定式化[[ユークリッド幾何学]]を除く) [[図形の合同|側角側公理]] 、等しく「長い」両側と、それらの間に同じ角度を有する2つの三角形は、典型的ではないとして[[図形の合同|合同]]上記側面はに起こる場合を除き平行になる。 |
|||
=== サークル === |
|||
[[ファイル:TaxicabGeometryCircle.svg|右|サムネイル|276x276ピクセル| 離散および連続したタクシージオメトリの円 ]] |
|||
[[円 (数学)|円]]は、 ''中心''と呼ばれる点から、 ''[[半径]]''と呼ばれる固定距離の点のセットである。 タクシージオメトリでは、距離はユークリッドジオメトリとは異なるメトリックによって決定され、円の形状も変化する。 タクシーの円は、座標軸に対して45度の角度で側面が向けられた[[正方形]]である。 右の図は、これが真実である理由を示している。青で示されている、中心からの距離が固定されたすべてのポイントのセットを赤で示している。 街区のサイズが小さくなると、ポイントはより多くなり、連続したタクシージオメトリで回転した正方形になる。 両側に長さがあるが<math>\sqrt{2}r</math> [[ユークリッド距離|ユークリッド計量]]を使用する ''。r''は円の半径で、タクシージオメトリの長さは2 ''r''である。 したがって、円の円周は8 ''r''である。 したがって、幾何学的なアナログの値は[[円周率|<math>\pi </math>]]このジオメトリでは4である。 タクシージオメトリの単位円の式は次のとおりである。 <math>|x| + |y| = 1</math> [[直交座標系|デカルト座標]]で |
|||
: <math>r = \frac{1}{| \sin \theta| + |\cos\theta|}</math> |
|||
半径1の円(この距離を使用)は、その中心のフォンノイマン近傍である。 |
|||
以下のための半径''r''の円[[チェビシェフ距離]] ( [[Lp空間|<sub>L∞</sub>メトリック]]平面上の)はチェビシェフ距離を平面タクシー距離に回転及びスケーリングによって同等とみなすことができるので、平面、また座標軸に辺の長さ2 ''r個の''並列の正方形である。 ただし、L <sub>1</sub>と<sub>L∞</sub>メトリックの間のこの等価性は、より高い次元に一般化されない。 |
|||
これらの円のコレクションの各ペアに空でない交差がある場合は常に、コレクション全体の交差ポイントが存在する。したがって、マンハッタン距離は単射距離空間を形成する 。 |
|||
== 用途 == |
|||
=== チェスの距離の測定 === |
|||
[[チェス]]では、 [[ルーク]]の[[チェスボード|チェス盤上の]]正方形間の距離は、タクシー距離で測定される。 [[キング (チェス)|王]]と[[クイーン (チェス)|女王]]は[[チェビシェフ距離|チェビシェフ距離を]]使用し、 [[ビショップ|司教]]は45度回転したチェス盤の(同じ色の正方形の間の)タクシー距離、つまり対角線を座標軸として使用する。 ある正方形から別の正方形に到達するには、キングのみがそれぞれの距離に等しい移動数を必要とする。ルーク、クイーン、ビショップは1つか2つの移動が必要である(空のボード上で、ビショップの場合はまったく移動が可能であると想定している)。 |
|||
=== 圧縮センシング === |
|||
劣決定の線形方程式系を解く場合、パラメーターベクトルの[[正則化|正則]]化項は、 <math>\ell_1</math> -ベクトルのノルム(タクシージオメトリ)。 <ref>{{Cite journal|last=Donoho|first=David L.|date=March 23, 2006|title=For most large underdetermined systems of linear equations the minimal <math>\ell_1</math>-norm solution is also the sparsest solution|journal=Communications on Pure and Applied Mathematics|volume=59|issue=6|pages=797–829|DOI=10.1002/cpa.20132}}</ref> このアプローチは、 [[圧縮センシング]]と呼ばれる信号回復フレームワークに現れる。 |
|||
=== 頻度分布の違い === |
|||
タクシージオメトリは、離散度数分布の違いを評価するために使用できる。 たとえば、 RNAスプライシングでは、スプライスサイトの近くの各特定の[[ヌクレオチド]]に各ヘキサマーが出現する確率をプロットする[[オリゴマー|ヘキサマーの]]位置分布をL1距離と比較できる。 各位置分布は、各エントリが特定のヌクレオチドで始まる六量体の可能性を表すベクトルとして表すことができる。 2つのベクトル間のL1距離が大きい場合は、分布の性質に大きな違いがあることを示し、距離が小さい場合は、同様の形状の分布を示する。 これは、各セグメントの面積がそのポイントでの2つの曲線の尤度の絶対差であるため、2つの分布曲線間の面積を測定することと同じである。 すべてのセグメントについて合計すると、L1距離と同じ測定値を提供する。 <ref name="lim">{{Cite journal|last=Lim|first=Kian Huat|last2=Ferraris|first2=Luciana|last3=Filloux|first3=Madeleine E.|last4=Raphael|first4=Benjamin J.|last5=Fairbrother|first5=William G.|date=July 5, 2011|title=Using positional distribution to identify splicing elements and predict pre-mRNA processing defects in human genes|journal=Proceedings of the National Academy of Sciences of the United States of America|volume=108|issue=27|pages=11093–11098|bibcode=2011PNAS..10811093H|DOI=10.1073/pnas.1101135108|PMID=21685335|PMC=3131313}}</ref> |
|||
== 例 == |
== 例 == |
||
| 16行目: | 60行目: | ||
[[チェス]]では、[[ルーク]]にとってのマス間の距離はマンハッタン距離によって測られる([[キング (駒)|キング]]・[[クイーン (駒)|クイーン]]や[[ビショップ]]は[[チェビシェフ距離]]を用いる)。 |
[[チェス]]では、[[ルーク]]にとってのマス間の距離はマンハッタン距離によって測られる([[キング (駒)|キング]]・[[クイーン (駒)|クイーン]]や[[ビショップ]]は[[チェビシェフ距離]]を用いる)。 |
||
== 歴史 == |
|||
{{DEFAULTSORT:まんはつたんきより}} |
|||
''L'' <sup>1</sup>メトリックは、 [[ルジェル・ヨシプ・ボスコヴィッチ|Roger Joseph Boscovich]]によって1757年に[[回帰分析]]で使用されました。 <ref name="Stigler1986">{{Cite book|last=Stigler|first=Stephen M.|year=1986|title=The History of Statistics: The Measurement of Uncertainty before 1900|publisher=Harvard University Press|isbn=9780674403406|url=https://archive.org/details/historyofstatist00stig|accessdate=October 6, 2019}}</ref> 幾何学的解釈は19世紀後半にまでさかのぼり、 [[非ユークリッド幾何学|非ユークリッド幾何学の]]発展、特に[[ヘルマン・ミンコフスキー|ヘルマンミンコウスキー]]とその[[ミンコフスキーの不等式]]によるものである。この幾何学は、特に数の幾何学で使用される特別なケースである{{Harv|Minkowski|1910}} 。 [[Lp空間|''L'' <sup>p</sup>空間]]の形式化は{{Harv|Riesz|1910}} である。 |
|||
| ⚫ | |||
== 関連項目 == |
|||
* [[ノルム線型空間|ノルムベクトル空間]] |
|||
* [[距離函数|メトリック]] |
|||
* 直交凸包 |
|||
* [[ハミング距離]] |
|||
* [[15パズル]] |
|||
* [[ランダムウォーク]] |
|||
* マンハッタンの配線 |
|||
== ノート == |
|||
{{Reflist}} |
|||
== 参考文献 == |
|||
* {{Cite book|first=Eugene F.|last=Krause|title=Taxicab Geometry|url=https://archive.org/details/taxicabgeometrya0000krau|year=1987|publisher=Dover|isbn=978-0-486-25202-5}} |
|||
* {{Cite book|last=Minkowski|first=Hermann|author-link=Hermann Minkowski|title=Geometrie der Zahlen|url=https://archive.org/details/geometriederzahl00minkrich|publisher=R. G. Teubner|location=Leipzig and Berlin|mr=0249269|year=1910|jfm=41.0239.03|accessdate=October 6, 2019|language=de}} |
|||
* {{Cite journal|last=Riesz|first=Frigyes|author-link=Frigyes Riesz|year=1910|title=Untersuchungen über Systeme integrierbarer Funktionen|journal=Mathematische Annalen|volume=69|issue=4|pages=449–497|language=de|DOI=10.1007/BF01457637}} |
|||
== 外部リンク == |
|||
* {{MathWorld|title=Taxicab Metric}} |
|||
* {{Cite web|url=http://www.ams.org/publicoutreach/feature-column/fcarc-taxi|title=Taxi!|first=Joe|author=Malkevitch|website=American Mathematical Society|date=October 1, 2007|accessdate=October 6, 2019}} |
|||
| ⚫ | |||
[[Category:ノルム]] |
|||
[[Category:計量幾何学]] |
|||
[[Category:デジタル幾何学]] |
[[Category:デジタル幾何学]] |
||
[[Category:数学に関する記事]] |
|||
2020年8月31日 (月) 19:28時点における版

マンハッタン距離(マンハッタンきょり、Manhattan distance)またはL1-距離、タクシーの幾何、 直線距離 、 L 1距離 、 L 1距離、ノルム ( L p spaceを参照)、 スネーク距離 、 シティブロック距離は、幾何学における距離概念のひとつ。各座標の差(の絶対値)の総和を2点間の距離とする。
ユークリッド幾何学における通常の距離(ユークリッド距離)に代わり、この距離概念を用いた幾何学はタクシーの幾何 (taxicab geometry) と呼ばれる。19世紀にヘルマン・ミンコフスキーによって考案された。
通常の距離関数またはユークリッド幾何学のメトリックが、2点間の距離がデカルト座標の絶対差の合計である新しいメトリックで置き換えられる幾何学の形式である。 。 [1] マンハッタン距離の名前は、 マンハッタン島のほとんどの道路のグリッドレイアウトを暗示している 。これにより、車が自治区内の2つの交差点間を移動できる最短距離は、タクシージオメトリの交差点の距離と同じになる。
ジオメトリは18世紀から回帰分析で使用されており、今日ではしばしばLASSOと呼ばれている。 幾何学的解釈は、19世紀の非ユークリッド幾何学にさかのぼり、 ヘルマンミンコフスキーによるものである。
正式な定義
タクシー距離、 、2つのベクトル間 デカルト座標系が固定されたn次元の実数 ベクトル空間では、 座標軸への点間の線分の投影の長さの合計である。 より正式には、
は ベクトルである。
たとえば、 飛行機では、タクシーの距離そしてである
より形式的には、2点間の距離を直交する座標軸に沿って測定することで一般の 次元空間においてマンハッタン距離 が定義される。
ただし、, とおいた。例えば、平面上において座標 に置かれた点 と、座標 に置かれた点 間のマンハッタン距離は
となる。
プロパティ
タクシー距離は、座標系の回転に依存するが、座標軸に関するその反射またはその並進には依存しない。 全てのマンハッタン距離を満たすヒルベルトの公理 (の定式化ユークリッド幾何学を除く) 側角側公理 、等しく「長い」両側と、それらの間に同じ角度を有する2つの三角形は、典型的ではないとして合同上記側面はに起こる場合を除き平行になる。
サークル
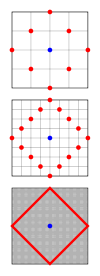
円は、 中心と呼ばれる点から、 半径と呼ばれる固定距離の点のセットである。 タクシージオメトリでは、距離はユークリッドジオメトリとは異なるメトリックによって決定され、円の形状も変化する。 タクシーの円は、座標軸に対して45度の角度で側面が向けられた正方形である。 右の図は、これが真実である理由を示している。青で示されている、中心からの距離が固定されたすべてのポイントのセットを赤で示している。 街区のサイズが小さくなると、ポイントはより多くなり、連続したタクシージオメトリで回転した正方形になる。 両側に長さがあるが ユークリッド計量を使用する 。rは円の半径で、タクシージオメトリの長さは2 rである。 したがって、円の円周は8 rである。 したがって、幾何学的なアナログの値はこのジオメトリでは4である。 タクシージオメトリの単位円の式は次のとおりである。 デカルト座標で
半径1の円(この距離を使用)は、その中心のフォンノイマン近傍である。
以下のための半径rの円チェビシェフ距離 ( L∞メトリック平面上の)はチェビシェフ距離を平面タクシー距離に回転及びスケーリングによって同等とみなすことができるので、平面、また座標軸に辺の長さ2 r個の並列の正方形である。 ただし、L 1とL∞メトリックの間のこの等価性は、より高い次元に一般化されない。
これらの円のコレクションの各ペアに空でない交差がある場合は常に、コレクション全体の交差ポイントが存在する。したがって、マンハッタン距離は単射距離空間を形成する 。
用途
チェスの距離の測定
チェスでは、 ルークのチェス盤上の正方形間の距離は、タクシー距離で測定される。 王と女王はチェビシェフ距離を使用し、 司教は45度回転したチェス盤の(同じ色の正方形の間の)タクシー距離、つまり対角線を座標軸として使用する。 ある正方形から別の正方形に到達するには、キングのみがそれぞれの距離に等しい移動数を必要とする。ルーク、クイーン、ビショップは1つか2つの移動が必要である(空のボード上で、ビショップの場合はまったく移動が可能であると想定している)。
圧縮センシング
劣決定の線形方程式系を解く場合、パラメーターベクトルの正則化項は、 -ベクトルのノルム(タクシージオメトリ)。 [2] このアプローチは、 圧縮センシングと呼ばれる信号回復フレームワークに現れる。
頻度分布の違い
タクシージオメトリは、離散度数分布の違いを評価するために使用できる。 たとえば、 RNAスプライシングでは、スプライスサイトの近くの各特定のヌクレオチドに各ヘキサマーが出現する確率をプロットするヘキサマーの位置分布をL1距離と比較できる。 各位置分布は、各エントリが特定のヌクレオチドで始まる六量体の可能性を表すベクトルとして表すことができる。 2つのベクトル間のL1距離が大きい場合は、分布の性質に大きな違いがあることを示し、距離が小さい場合は、同様の形状の分布を示する。 これは、各セグメントの面積がそのポイントでの2つの曲線の尤度の絶対差であるため、2つの分布曲線間の面積を測定することと同じである。 すべてのセグメントについて合計すると、L1距離と同じ測定値を提供する。 [3]
例
マンハッタン距離は、都市ブロック距離(city block distance, 市街地距離)としても知られている。マンハッタン距離の名は、マンハッタンのような正方形のブロックに区分された都市で、自動車が運転される距離に由来する。ある角から東に 3 ブロック、北に 6 ブロックの位置にある角まで移動するには、いかなる経路を辿っても最低 9 ブロックを通過せねばならない。
チェスでは、ルークにとってのマス間の距離はマンハッタン距離によって測られる(キング・クイーンやビショップはチェビシェフ距離を用いる)。
歴史
L 1メトリックは、 Roger Joseph Boscovichによって1757年に回帰分析で使用されました。 [4] 幾何学的解釈は19世紀後半にまでさかのぼり、 非ユークリッド幾何学の発展、特にヘルマンミンコウスキーとそのミンコフスキーの不等式によるものである。この幾何学は、特に数の幾何学で使用される特別なケースである(Minkowski 1910) 。 L p空間の形式化は(Riesz 1910) である。
関連項目
ノート
- ^ Black. “Manhattan distance”. Dictionary of Algorithms and Data Structures. 2019年10月6日閲覧。
- ^ Donoho, David L. (March 23, 2006). “For most large underdetermined systems of linear equations the minimal -norm solution is also the sparsest solution”. Communications on Pure and Applied Mathematics 59 (6): 797–829. doi:10.1002/cpa.20132.
- ^ Lim, Kian Huat; Ferraris, Luciana; Filloux, Madeleine E.; Raphael, Benjamin J.; Fairbrother, William G. (July 5, 2011). “Using positional distribution to identify splicing elements and predict pre-mRNA processing defects in human genes”. Proceedings of the National Academy of Sciences of the United States of America 108 (27): 11093–11098. Bibcode: 2011PNAS..10811093H. doi:10.1073/pnas.1101135108. PMC 3131313. PMID 21685335.
- ^ Stigler, Stephen M. (1986). The History of Statistics: The Measurement of Uncertainty before 1900. Harvard University Press. ISBN 9780674403406 2019年10月6日閲覧。
参考文献
- Krause, Eugene F. (1987). Taxicab Geometry. Dover. ISBN 978-0-486-25202-5
- Minkowski, Hermann (1910) (ドイツ語). Geometrie der Zahlen. Leipzig and Berlin: R. G. Teubner. JFM 41.0239.03. MR0249269 2019年10月6日閲覧。
- Riesz, Frigyes (1910). “Untersuchungen über Systeme integrierbarer Funktionen” (ドイツ語). Mathematische Annalen 69 (4): 449–497. doi:10.1007/BF01457637.
外部リンク
- Weisstein, Eric W. "Taxicab Metric". mathworld.wolfram.com (英語).
- Malkevitch (2007年10月1日). “Taxi!”. American Mathematical Society. 2019年10月6日閲覧。























