ベクレル

ベクレル becquerel
記号	Bq
系	国際単位系 (SI)
種類	組立単位
量	放射能の量
組立	s-1
定義	放射性核種の壊変数が1秒間に1の割合である放射能
語源	アンリ・ベクレル

ベクレル（英語：becquerel、記号: Bq）とは、放射能の量を表す単位で、SI組立単位の1つである。1秒間に放射性核種が1個崩壊すると1 Bqである。

概要

はじめに1ベクレルあった放射性物質がどれだけの速さで減衰するのか表したグラフ。放射能(単位はベクレルなど)も指数関数的に減衰する。崩壊定数は半減期に反比例するため、崩壊定数が大きい(=半減期が短い)ほど早く減衰していることがわかるだろう。グラフで上の線ほど崩壊定数が小さいため減衰していないが一番下では凄まじい速さで減衰しているのがわかる。ここでy軸が放射能(単位:ベクレル)、x軸は時間の単位を秒ととった場合半減期は有効数字3桁で上から17.3秒、3.47秒、0.693秒、0.139秒、0.0277秒である。

例えば、毎秒370個の放射性核種（原子核）が崩壊して放射線を発している場合、その放射能は370 Bqとなる。時間経過により変化するため半減期の極めて短い放射性核種や半減期は十分長いものの半減期よりも十分長い時間が経過した場合の詳細な計算法は後述する。ここでは概要のみ述べる。

ベクレルは時間が経過するとともに減少するのだというと、とくに半減期が1秒にすら満たない核種や素粒子ではBqで表せるのか疑う読者もいるかもしれないが、物理的には放射能(単位はベクレルなど)はλNと微分で表す物理量であるため崩壊定数さえ分かれば理論値は計算できるため問題は起こらない。また実測値は1秒間の崩壊数というのは整数になるではないかと言われるかもしれないが、このような事情のためベクレルの数値は小数で表すことは普通であり、整数条件を満足する必要性はない。

更には半減期が経過すると原子数は半分になるわけであるが、放射能は微分で定義され原子数と崩壊定数の積で表せるため同様に半減期が経過すればベクレルもまたちょうど半分になるというのもただちにわかる。すなわち原子数のみならず放射能に対しても同一の半減期で減衰すると理解でき、同様に計算できるわけである。

例えば1万ベクレルの(出入りのない)放射性物質があり、半減期が経過すれば5000ベクレルに減衰するというわけである。1ベクレルの場合半減期が経過すれば0.5ベクレルと減衰していく。指数関数的減衰のためゼロにはならないが、原子数は有限であり原子数が少なくなればポアソン過程で表現されるうえ、最終的にはゼロまたは化学分析や放射線測定が困難なレベルにまで減衰する。太陽系創世時の半減期の短い(とはいえ短いというのは、地球の年齢46億年に対してだが)、核種の放射能はこのような運命を辿ったとされている。

実験的に放射能を測定する場合、対象の物質や性質がわかっているなら、放射能が時間変化で急激変化しない場合はカウント数と放射能の強さをあらかじめ測定しておいて、相対的な差で放射能を測定するなどの手法が用いられる。半減期が極めて短い原子核・素粒子の放射能の測定手法の詳細はここでは論じないが、相当高感度・高性能の測定器が求められる。

逆に半減期が極めて長い場合や放射能が極めて低い場合もめったに放出しない放射線を確実に検出せねばならないため、これも高い技術力が要求される。高木仁三郎は大学教員時代、超微量の放射能測定器を開発していたが、核実験フォールアウトによる遮蔽材として使われる鉄の汚染が問題となっていた。

これら測定技術は素粒子物理学や超ウラン元素の実験的研究、宇宙線の観測等でとくに重要となる。粒子検出器も参照せよ。

名称と表現

ベクレルという名称は、ウランの放射能を発見しノーベル物理学賞を受賞したフランスの物理学者アンリ・ベクレルに因む。かつては壊変毎秒（かいへんまいびょう、dps; decays per second / disintegrations per second）と言ったが1975年の国際度量衡総会にて、この名称になった。

ベクレルは、SI基本単位では[s^-1]と表される。T ^-1の次元を持つが、放射能の計量以外には使用できない。同じT ^-1の次元を持つ単位にはヘルツ（Hz）や毎秒（s^-1）がある。

ベクレルは数値の桁が大きくなるため、kBq（kilobecquerel, 10³Bq）、MBq（megabecquerel, 10⁶Bq）、GBq (gigabecquerel, 10⁹Bq）、TBq（terabecquerel, 10¹²Bq）などのSI接頭辞を使用することが多い。ミリベクレルなどの小さいほうのものもよく用いられる。単位としてのベクレルをフルスペルで英字表記する場合は常に小文字で「becquerel」と書かねばならず、単位記号では「Bq」と頭文字だけを大文字にすると国際単位系のルールで規定されている。

かつては、1gのラジウムの放射能を表すキュリー（記号Ci）という単位が用いられていた。

• 1Ci＝3.7×10¹⁰Bq＝37GBq
• 1Bq＝2.7×10⁻¹¹Ci=27pCi

放射能の量[Bq] と 放射線の強さ[Gy]、[Sv]

ベクレルなどの放射能の単位は、放射性物質から放射線がどのぐらいでてくるのかという事を表す物理量であり、出てきた後の放射線が物質や人体とどのように相互作用するのかはベクレルだけわかっても一切わからない。それらを評価するにはこの節で書いたような情報が必要だということである。この図はアルファ線、ベータ線、ガンマ線、中性子線と物質との相互作用を簡単に表したものである。アルファ線やベータ線は電荷を持っており電離作用が強い。アルファ線は電離作用は凄まじいが飛距離は少ない。短い距離で多くの分子を電離し破壊する。ベータ線は軽いので弾き飛ばされやすく、空気中など密度の低い物質内ではジグザグに動き、水中など密度の高い物質内ではアルファ線同様ほとんど飛ばずに近くの分子を電離する。電離させた電子も電離作用をもっていて、これをデルタ線とよぶ。ガンマ線はエネルギーによってエネルギーが低い順に光電効果・コンプトン効果・対生成・光核反応を引き起こす。中性子線については下図の解説を参照。

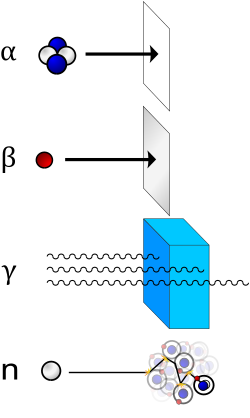
出てきた放射線は物質と相互作用して速さが遅くなっていき、やがて停止する。この図はアルファ線、ベータ線、ガンマ線を遮蔽するには何が必要かをあらわしている。アルファ線は紙一枚で停止させられるが、ガンマ線はたくさんの水でも全て止めるとができない(ガンマ線自体指数関数的減衰であるからどのみちゼロにはできないのだが)。特に人体の影響を計算する時も人体の大半が水であると計算するため、ガンマ線は人体も貫通するということである。一番下が中性子線であり、とくに水素の原子核である陽子のような軽い原子核と衝突することによって停止する。その過程で原子核を弾き飛ばしたり(これが電離作用をもつ)、ガンマ線を放出したりする。中性子自体も10分の半減期で陽子へと壊変する。人体の大半は水や有機化合物といった水素原子や軽元素を大量に含むため、中性子線の影響を受けやすいといえるのである。

冒頭で前述したようにベクレルは放射能の量を現す単位である。一方、放射線の吸収線量を表す単位はグレイ(単位記号：[Gy] ) であり、被曝による生物学的影響の大きさ（線量当量）の単位がシーベルト(単位記号：[Sv] ) である。人体への影響を評価するにはこれらの単位を用いねばならない。

同ベクレルの放射能が存在しても人体への影響を評価するには、線源の形状・遮蔽の評価、吸収線量や線量当量の強さは条件によって異なる。

すなわち、放射性物質が異なれば例え放射能が同量であっても、放出する放射線の種類やエネルギーは異なるであろうし、どのような状態で放射性物質が存在するのか、測定位置までの距離はどのぐらいあるか、測定者と線源との間にある物質の遮蔽によりどのぐらい放射線が遮られるかなどによっても影響が変わってくるため、その他の情報を一切伏せてただ放射能が合計何ベクレルある、というだけでは判断のしようがないのである。またシーベルトからベクレルに換算することもそういった条件がわからない限り難しいといえる。

冒頭でキュリーとベクレルを換算しているが、これがなぜできるのかといえば、放射性物質が何回崩壊したかという同じ量だから簡単に換算できるわけである。例えば長さ同士であればセンチとインチなどの単位が違っても換算できるが、長さと重さなどのそもそも単位そのものが違うならば換算が不可能だということである。放射能単位であるベクレルから人体影響を評価するシーベルトへの換算は長さと重さほど全く違う量ではないものの、様々な条件が重要となってくるためそれがわからないなら簡単に換算は不可能である。例えば同一のロープの長さと重さということであれば相互に換算ができるだろうが、種類の違うものの長さと重さとなるとその違いがわからないと換算ができないことからもわかるだろう。

もちろんベクレルからシーベルトへの換算が絶対に不可能というのではなく、さまざまな条件がわからない限り単純計算では難しいというわけである。

ベクレルと原子核の個数との関係

→詳細は「比放射能」を参照

→詳細は「半減期」を参照

単位時間あたりにN個の放射性の原子核(以下原子数という)が崩壊する確率は、崩壊定数に比例し、その半減期T_1/2に反比例する。これは

$\lambda ={\frac {\ln(2)}{T_{1/2}}}$

単位時間あたりに崩壊する量を表すという崩壊定数の定義および、上記式より半減期が長くなると崩壊定数が小さくなる(=反比例する)ということよりただちにわかる。放射壊変の微分方程式

$-{\frac {dN(t)}{dt}}=\lambda {N}$

より、放射能は右辺で定義されるから、放射能の単位であるベクレルはその核種の崩壊定数λまたは半減期T_1/2(いずれも時間の単位は秒を取らねばならない)と原子数Nとで一意に定まる。

この微分方程式を初期条件 t=0のときの原子数を$N_{0}$個とすると、時刻tにおける原子数は

$N(t)=N_{0}e^{-\lambda {t}}$

となる。定義によりこれを微分したときに両辺に-1を掛けた量が放射能であるから、任意の時刻tにおける放射能Bq(t)は

$Bq(t)=\lambda {N}_{0}e^{-\lambda {t}}$

であることがわかる。t=0とおくとe^-λ0=1であるから、時間変化を考えない場合は原子数と崩壊定数の二つが定まればその放射性物質の放射能が求められるということがわかる。つまり二変数函数であるといえる。

ベクレルから質量や原子数や半減期を計算したりする方法は比放射能を参照せよ。またこの式は一次反応を仮定しており、娘核種も放射能を持っていて、時間変化により親・娘量核種の総放射能を求めるといった場合連立微分方程式を解かねばならない。簡単なものは半減期に計算例がある。これらの半減期の長さによって任意の時間が経過したときの放射能の強さは放射平衡によって論じられる。

1グラムのラジウムの放射能

ここでは具体例として、1グラムのラジウムに何個のラジウム原子核が含まれていて、それが何ベクレルの放射能を持っているのか実際に計算する。そのためには上述したように、原子数に単位を秒で取った崩壊定数をかければよい。

純粋な(ほかの物質が混じっていない)1gのラジウム226にはアボガドロ定数をA=6.02ｘ10²³としたとき、A割る質量数=原子数であるから、

$N={\frac {A}{226}}\approx {2.66\times {10}^{21}}$

すなわち約2.66×10²¹個(2兆6600億の10億倍個)の原子核が含まれることがわかる。

ラジウム226の半減期T_1/2は1600年であり、これを秒に換算すれば

1600 [年] = 1600x365x24x60²≒5.05ｘ¹⁰[秒]

すなわちラジウム226の半減期は5.05ｘ10¹⁰秒(505億秒)である。次に崩壊定数を求めよう。崩壊定数λはln(2)/T_1/2であったから求めた半減期を代入し、

$\lambda ={\frac {\ln(2)}{5.05\times 10^{10}}}\approx {\frac {0.693}{5.05\times 10^{10}}}\approx 1.37\times 10^{-11}$

となる。放射能を計算するためλNを求めれば、

$1.37\times 10^{-11}\times 2.66\times 10^{21}\approx 3.64\times 10^{10}$

約3.64x10¹⁰ベクレルであるといえる。当初のキュリーCiの定義はラジウム1グラムの放射能で3.7x10¹⁰であったから、有効数字3桁で計算した上の計算例は小数点第二位を繰り上げれば一致することがわかる。

この場合のラジウム226は時間と共に崩壊によって減少していくので、計算するにあたっては経過時間を考慮する必要がある。また時刻t>0における放射能は、崩壊後の核種が放射性である場合、その核種と親核種との放射能の総和はによる放射能の分が増えるのでλN[Bq]より大きくなる。

関連項目

• 放射能の単位
  • 壊変毎分
  • キュリー - Ci
  • ラザフォード - Rd
  • マッヘ - M.E.
• 吸収線量・放射線量の単位
  • シーベルト - Sv
  • ラド - rad
  • グレイ - Gy
  • レム - rem
  • レントゲン - R
• 放射性崩壊
  • 放射能
  • 比放射能
  • 半減期
  • 崩壊定数
  • 指数関数的減衰
• SI接頭辞 - キロ・メガやミリ・マイクロなどの単位の前につけて倍数を表す記号。3ケタずつ変化する。日本語では4ケタずつ位取りが変化するので換算時に注意。
• 柴崎力栄 - 大阪工業大学の准教授で「弁当にベクレルが入っている」とツイッターに書き込み話題となった[1]。放射性物質は味覚で感じ取ることはできない。