過剰適合

ノイズのある、ほぼ線形なデータは、一次関数にも多項式関数にも適合する。多項式関数は各データポイントを通過し、一次関数は必ずしもデータポイントを通過しないが、端の方で大きな変化が生じることがないため、一次関数の方がよりよい適合であると言える。回帰曲線を使ってデータを外挿した場合、過剰適合であれば悪い結果となる。

教師あり学習（ニューラルネットワークなど）における過剰適合。訓練時のエラーを青、評価時のエラーを赤で示している。訓練時のエラーが減少しているのに、評価時のエラーが増えている場合、過剰適合が起きている可能性がある。

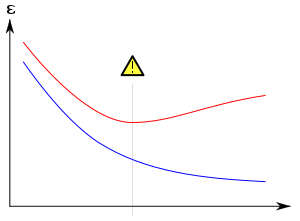
過剰適合（英: Overfitting）とは、統計学や機械学習において、訓練データに対して学習されているが、未知データに対しては適合できていない、汎化できていない状態を指す。汎化能力の不足に起因する。

その原因の一つとして、統計モデルへの適合の媒介変数が多すぎる等、訓練データの個数に比べて、モデルが複雑で自由度が高すぎることがある。不合理で誤ったモデルは、入手可能なデータに比較して複雑すぎる場合、完全に適合することがある。

機械学習

機械学習の分野では過学習とも呼ばれる。過剰適合の概念は機械学習でも重要である。通常、学習アルゴリズムは一連の訓練データを使って訓練される。つまり、典型的な入力データとその際の既知の出力結果を与える。学習者はそれによって、訓練データでは示されなかった他の例についても正しい出力を返すことができるようになると期待される。しかし、学習期間が長すぎたり、訓練データが典型的なものでなかった場合、学習者は訓練データの特定のランダムな（本来学習させたい特徴とは無関係な）特徴にまで適合してしまう。このような過剰適合の過程では、訓練データについての性能は向上するが、それ以外のデータでは逆に結果が悪くなる。

ニューラルネットワークの訓練における過剰適合の過程をオーバートレーニング（Overtraining）とも呼ぶ。

正則化

機械学習や統計学において、媒介変数を減らすのではなく、誤差関数に正則化項を追加して、モデルの複雑度・自由度に抑制を加え、過学習を防ぐ方法がある。Tikhonov 正則化（Tikhonov Regularization）やLASSOなどがある[1]。

サポートベクターマシンにおいては、媒介変数（パラメータ）を減らすのではなく、マージンを最大化することにより、過学習を防いでいて、これも、Tikhonov 正則化と同じような手法に基づいている。

参照：逆問題

交差検定

統計学の場合も機械学習の場合も、追加の技法（交差検定、早期打ち切り(early stopping)）を用いることによって、過剰適合に陥らず、訓練がよりよい一般化となっていることを確認し、かつ示す必要がある。

参考文献

• Tetko, I.V.; Livingstone, D.J.; Luik, A.I. Neural network studies. 1. Comparison of Overfitting and Overtraining, J. Chem. Inf. Comput. Sci., 1995, 35, 826-833