ニューラルネットワーク

人工知能の分野におけるニューラルネットワーク（英: neural network; NN、神経網）は、生物の学習メカニズムを模倣した機械学習手法として広く知られているものであり、「人工ニューロン」と呼ばれる計算ユニットをもち、生物の神経系のメカニズムを模倣しているものである。人間の脳の神経網を模した数理モデル。模倣対象となった生物のニューラルネットワーク（神経網）とはっきり区別する場合は、人工ニューラルネットワーク (英: artificial neural network) と呼ばれる。

以下では説明の都合上、人工的なニューラルネットワークのほうは「人工ニューラルネットワーク」あるいは単に「ニューラルネットワーク」と呼び、生物のそれは「生物のニューラルネットワーク」あるいは「生物の神経網」、ヒトの頭脳のそれは「ヒトのニューラルネットワーク」あるいは「ヒトの神経網」と表記することにする。

概要

生物のニューロン

人工ニューラルネットワークを理解するには、そもそもそれがどのようなものを模倣しようとしているのかを知っておく必要があるので説明する。ヒトの神経系にはニューロンという細胞があり、ニューロン同士は互いに軸索 (axon) と樹状突起 (dendrite) を介して繋がっている。ニューロンは樹状突起で他の神経細胞から情報を受け取り、細胞内で情報処理してから、軸索で他のニューロンに情報を伝達する。そして、軸索と樹状突起が結合する部分をシナプス(synapse)という（右図も参照。クリックして拡大して見ていただきたい。紫色の部分がひとつのニューロンであり、Dendrite, Axonなどが示されている。）。　このシナプスの結合強度というのは、外的な刺激に反応してちょくちょく変化する。このシナプス結合強度の変化こそが生物における「学習」のメカニズムである。

人工ニューロン

ヒトの神経網を模した人工ニューラルネットワークでは、計算ユニットが《重み》を介して繋がり、この《重み》がヒトの神経網のシナプス結合の「強度」と似た役割を担っている。各ユニットへの入力は《重み》によって強さが変化するように作られており、ユニットにおける関数計算に影響を与える。ニューラルネットワークというのは、入力用ニューロンから出力用ニューロンへと向かって計算値を伝播させてゆくが、その過程で《重み》をパラメータとして利用し、入力の関数を計算する。（ただし計算値が出力用ニューロンへと伝播されてゆくというだけでは入力パターンからある決まった出力パターンが出るだけなので、さほど有益というわけではない。）《重み》が変化することで「学習」が起きる（ここが重要なのである）。

（右図も参照のこと。右図で「weights」や、丸で囲まれた「w」が縦に並んでいるのが《重み》である。）

生物のニューラルネットワークに与えられる外的刺激に相当するものとして、人工ニューラルネットワークでは「訓練データ」が与えられる。いくつか方法があるが、たとえば訓練データとして入力データと出力ラベルが与えられ、たとえば何かの画像データとそれについての正しいラベルが与えられる（たとえばリンゴの画像データとappleというラベル、オレンジの画像データとorangeというラベルが与えられる）。ある入力に対して予測される出力が本当のラベルとどの程度一致するかを計算することで、ニューラルネットワークの《重み》についてフィードバックを得られ、ニューロン間の《重み》は誤差（予測誤差）に応じて、誤差が減少するように調整される。多数のニューロン間で《重み》の調整を繰り返し行うことで次第に計算関数が改善され、より正確な予測をできるようになる。（たとえばオレンジの画像データを提示されると「orange」と正しいラベルを答えられるようになる。） この《重み》の調整方法は、数学的にはバックプロパゲーションで偏微分して確率的勾配降下法で学習する方法である。

なお、ヒトのニューロンを模したユニットは人工ニューロンあるいはノードと呼ばれる。

相互作用ニューラルネットワークモデルの一例

右図の、多数のユニットが結合しネットワークを構成している数理モデルは、ニューラルネットワークのほんの一例である。（実際にはニューロンの数もさまざまに設定可能であるし、結合のしかたもさまざまに設定可能である。右図はあくまで、とりあえず説明にとりかかるための "一例" と理解いただきたい。 ユニットの構成（例: 線形変換の次元、非線形変換の有無・種類）やネットワークの構造（例: ユニットの数・階層構造・相互結合、入出力の再帰）に関して様々な選択肢があり、様々なモデルが提唱されている。）

各ユニットは入力のアフィン変換を必ず含み、多くの場合それに後続する非線形変換を含む（$unit({\boldsymbol {x}})=\sigma ({\boldsymbol {w}}{\boldsymbol {x}}+{\boldsymbol {b}})$）。

ニューラルネットワークは機械学習のモデルとして利用され、分類・回帰・生成など様々なクラスのタスクに教師あり/教師なし問わず利用される。利用分野にはパターン認識やデータマイニング（例: 画像認識、レコメンデーション）が挙げられる。学習法は確率的勾配降下法が主流である。

2層以上の多層パーセプトロンは微分可能で連続な任意の関数を近似できることが証明されている（線形分離不可能な問題を解ける）。

形式ニューロンなど研究の源流としては生物の神経系の探求であるが、その当初から、それが実際に生物の神経系のシミュレーションであるか否かについては議論がある。生物学と相互の進展により、相違点なども研究されている。

歴史

初期の研究

今日のディープニューラルネットワークは、200年以上前の統計学における初期の研究に基づいている。最も単純な種類のフィードフォワードニューラルネットワーク（FNN）は線形ネットワークであり、これは線形の活性化関数を持つ出力ノードの単一層で構成される。入力は一連の重みを介して直接出力に供給される。各ノードで重みと入力の積の合計が計算される。これらの計算された出力と与えられた目標値との間の平均二乗誤差は、重みを調整することによって最小化される。この技術は2世紀以上にわたって最小二乗法または線形回帰として知られている。これは、惑星の動きを予測するためにルジャンドル（1805年）およびガウス（1795年）によって、点集合に対する良好な近似線形フィットを見つける手段として使用された。 歴史的に、ノイマン型のようなデジタルコンピュータは、多数のプロセッサによるメモリへのアクセスを伴う明示的な命令の実行を介して動作する。一方、一部のニューラルネットワークは、コネクショニズムの枠組みを通じて生物学的システムにおける情報処理をモデル化しようとする試みから生まれた。ノイマン型とは異なり、コネクショニストの計算ではメモリと処理が分離されない。

形式ニューロン

1943年、ウォーレン・マカロックとウォルター・ピッツは、ニューラルネットワークのための学習しない計算モデルである「神経回路網理論」を考察した（形式ニューロンを参照）。このモデルは、研究を2つのアプローチに分岐させる道を開いた。1つのアプローチは生物学的プロセスに焦点を当て、もう1つのアプローチはニューラルネットワークの人工知能への応用に焦点を当てた。 1949年、ドナルド・ヘッブは、ヘッブの法則として知られるようになった「シナプスの可塑性の理論」という仮説を提案した。これは、ローゼンブラットのパーセプトロンやホップフィールド・ネットワークなど、多くの初期のニューラルネットワークで使用された。

1954年、ファーリーとクラークは、計算機を使用してヘッブ型ネットワークをシミュレートした。1956年、ロチェスター、ホランド、ハビット、デューダによって他のニューラルネットワーク計算機が作成された。

パーセプトロン

1958年、心理学者のフランク・ローゼンブラットは、最初に実装された人工ニューラルネットワークの1つであるパーセプトロンについて記述した。これは米国海軍研究局によって資金提供された。 R. D. ジョセフ（1960年）は、ファーリーとクラークによるさらに初期のパーセプトロンのような装置について言及している。「MITリンカーン研究所のファーリーとクラークは、パーセプトロンのような装置の開発において、実際にはローゼンブラットに先行していた」。しかし、「彼らはその主題を断念した」。

パーセプトロンは人工ニューラルネットワークの研究に対する世間の興奮を高め、米国政府は資金を大幅に増加させた。これは、パーセプトロンが人間の知能を模倣する能力に関する計算機科学者による楽観的な主張によって煽られた「AIの黄金時代」に貢献した。単純パーセプトロンには適応的な隠れ層がなかった。しかし、ジョセフ（1960年）は、適応的な隠れ層を持つ多層パーセプトロンについても議論した。1962年、ローゼンブラットは、H. D. ブロックと B. W. ナイトの研究も引用し、これらのアイデアを引用し採用した。残念ながら、これらの初期の取り組みは、隠れ層のための実用的な学習アルゴリズム、すなわち確率的勾配降下法にはつながらなかった。

1960年代と1970年代のディープラーニングのブレークスルー

1960年代と1970年代に人工ニューラルネットワークに関する基礎研究が行われた。

1965年、ソビエト連邦のアレクシー・イヴァネンコとラパによって、最初の実用的なディープラーニングアルゴリズムが示された。これは、任意に深いニューラルネットワークを訓練するための手法であるデータ処理のグループ手法であった。彼らはそれを多項式回帰の一形態、あるいはローゼンブラットのパーセプトロンの一般化と見なした。1971年の論文では、この手法で訓練された8層のディープネットワークが記述されており、これは回帰分析による層ごとの訓練に基づいている。余分な隠れユニットは、別の検証セットを使用して刈り込まれる。ノードの活性化関数はKolmogorov-Gabor. の多項式であるため、これらは乗法ユニットまたは「ゲート」を持つ最初のディープネットワークでもあった。

1967年、甘利俊一が多層パーセプトロンの確率的勾配降下法による学習を理論的に解析した論文を発表した。甘利の学生である斎藤庄司によるコンピュータ実験では、2つの修正可能な層を持つ2層の多層パーセプトロンが、線形分離不可能なパターンクラスを分類するために内部表現を学習し、日本語の修士論文で発表した。甘利俊一は1968年に書籍『情報理論II ―情報の幾何学的理論―』を出版し手法を解説した。扱っていたのは、入力が2次元ベクトル、出力がスカラーの二値分類問題で、1966年のR. O. Duda等の手書き文字認識のモデルを改変した $w^{(5)}\max\{W^{(1)}x,W^{(2)}x\}+w^{(6)}\min\{W^{(3)}x,W^{(4)}x\}$ という区分的線形識別関数のモデルである。甘利俊一は2023年の書籍『深層学習と統計神経力学』のp.69で、これを5層と数えているのだが、一般的なニューラルネットワークの層の数を数える際は、入力層は数えず、更に、甘利俊一は線形変換と活性化関数で2層と数えているが、普通はこれを1層と数え、よって、一般的な数え方では5層ではなく2層である。確率的勾配降下法は1951年に開発されたものであるが、『深層学習と統計神経力学』のp.7によると、甘利俊一は1967年当時その研究を知らなくて、確率的勾配降下法を再発見している。その後のハードウェアの発展とハイパーパラメータの調整により、エンドツーエンドの確率的勾配降下法は現在主流の訓練手法となっている。

ところが、1969年にマービン・ミンスキーとシーモア・パパートが単純パーセプトロンの限界（線形分離不可能なデータの判別問題を扱えないこと、排他的論理和回路を処理できないこと）を数学的に証明し、書籍『パーセプトロン』でそのことを記載したことで、1970年代になると神経回路網的手法に対する期待が一気にしぼみ、その研究者の数が急激に減ってしまった。なお、この単純パーセプトロンの限界は、上述の単純パーセプトロンではないイヴァフネンコと甘利が発表したニューラルネットワークには存在しなかった。甘利俊一の書籍『深層学習と統計神経力学』のp.9によると、彼らの書籍が原因というより、当時、東京大学の大型コンピューターを用いて計算していたが、256KBしかメモリがなく、当時のコンピューターの性能が低すぎたのがニューラルネットワークが流行らなかった原因であると述べている（なお、書籍には256KBではなく256Kワードと書かれているが、1966年11月1日に東京大学に納入されたHITAC 5020Eをさしているはずだが、これは64Kワードで1ワード32ビットのため、256KBである）。

1969年、福島邦彦はReLU（正規化線形ユニット）活性化関数を導入した。ReLUは、ディープラーニングで最も人気のある活性化関数となっている。

1976年、ニューラルネットワーク学習に転移学習が導入された。

誤差逆伝播法（バックプロパゲーション）の導入

バックプロパゲーション（誤差逆伝播法）とは、出力側から偏微分することで効率よく計算する手法である。1673年にゴットフリート・ヴィルヘルム・ライプニッツによって導出された連鎖律を使用する。自動微分ではトップダウン型（リバース・モード）と呼ばれる。

1962年、ローゼンブラットによって「back-propagating error correction procedure（誤差逆伝播訂正手順）」という用語が初めて用いられた。しかし、その時点ではこれを実装する方法を知らなかった。そして、これは言葉は似ているが、出力側からの偏微分の話ではない。

1960年、ヘンリー・J・ケリーはに制御理論の文脈で、誤差逆伝播法（バックプロパゲーション）の連続的な前駆体を発表していた。1964年に自動微分が発表され、その際発表されたのは入力側から偏微分する方法だが、1960年代後半に出力側から自動微分にて偏微分する方法が文章では発表されていなかったが提案はされていた。1970年、セッポ・リンナインマーは修士論文で誤差逆伝播法（バックプロパゲーション）の現代的な形式を発表し、文章で発表したのはこれが最初とされる。1971年、G.M. オストロフスキーらはそれを再発表した。1982年、ポール・ワーボスはニューラルネットワークに誤差逆伝播法（バックプロパゲーション）を適用した（彼の1974年の博士論文、1994年の著書で再版は、まだアルゴリズムを記述していなかった）。

1986年、デビッド・ラメルハートらが出力側から偏微分する方法をバックプロパゲーション（誤差逆伝播法）と命名する。論文は最急降下法を使用していたのだが、同時に確率的勾配降下法で学習する方法も定着する。確率的勾配降下法により、それまでの限界を突破する道がとうとう開け、「ニューラルネットワーク」として多くの研究者の注目を浴びるようになった。

畳み込みニューラルネットワーク（CNN）の導入

1979年、福島邦彦は、畳み込み層とダウンサンプリング層、および重み複製を備えた畳み込みニューラルネットワーク（CNN）のディープラーニングアーキテクチャを導入したネオコグニトロンを開発。畳み込みニューラルネットワークの一般的なダウンサンプリング手順であるmaxプーリング法も導入された。しかし、この時点では確率的勾配降下法による学習は行われていなかった。畳み込みニューラルネットワークはコンピュータビジョンに不可欠なツールとなっている。

1987年、アレックス・ウェイベルによって、音素認識にCNNを適用するための時間遅延ニューラルネットワーク（TDNN）が導入された。これは畳み込み、重み共有、およびバックプロパゲーションを使用した。 1988年、ウェイ・チャンはバックプロパゲーションで訓練されたCNNをアルファベット認識に適用した。

1989年、ヤン・ルカンらは、郵便物の手書きZIPコードを認識するためにLeNetと呼ばれるCNNを作成した。訓練には3日を要した。LeNet-5という、7層のCNNは、数字を分類するもので、いくつかの銀行で32×32ピクセルの画像にデジタル化された小切手の手書き数字を認識するために適用された。1990年、ウェイ・チャンは光コンピューティングハードウェア上にCNNを実装した。

1991年には、CNNが医用画像オブジェクトのセグメンテーションおよびマンモグラムにおける乳がん検出に応用された。 1988年以降、特に最初のカスケードネットワークが複数のシーケンスアラインメントによって生成された「プロファイル」（行列）で訓練されたとき、ニューラルネットワークの使用はタンパク質構造予測の分野を変革した。

リカレントニューラルネットワーク（RNN）の導入

リカレントニューラルネットワーク（RNN）は、2つの学問から見出された手法である。1つ目は統計力学であった。1972年、甘利俊一は、連想記憶のモデルとして、学習の要素を加えて、ヘッブの法則によってイジング模型の重みを修正することを提案した。これはジョン・ホップフィールド（1982年）によってホップフィールド・ネットワークとして普及した。

2つ目は神経科学であった。1901年、カハールは小脳皮質に「リカレント半円」を観察した。神経心理学者であったドナルド・ヘッブは、短期記憶の説明として「反響回路」を考察した。1943年、マカロックとピッツの論文では、サイクルを含むニューラルネットワークを考察し、そのようなネットワークの活動は、過去に無限に遡る活動の影響を受ける可能性がある、つまり再帰性があると指摘した。

1982年、アレイアーキテクチャを持つリカレントニューラルネットワーク（RNN）、すなわちクロスバー適応アレイ（Crossbar Adaptive Array）が導入された。このリカレントニューラルネットワークは、出力から教師（教示）入力への直接的な再帰接続を使用した。行動や決定を計算することに加えて、結果の状況の内部状態評価を計算した。外部教師を排除し、ニューラルネットワークに自己学習法を導入した。

1980年代初頭、認知心理学において、学術誌「American Psychologist」で、認知と感情の関係についての議論が行われた。1980年、ザイアンスは感情は最初に計算され、認知とは独立していると述べたが、1982年、ラザルスは、認知が最初に計算され、感情とは不可分であると述べた。1982年、クロスバー適応アレイは、認知と感情の関係のニューラルネットワークモデルを提示した。これは、AIシステムであるリカレントニューラルネットワーク（RNN）が、認知心理学によって同時に取り組まれた問題に貢献した議論の一例であった。 ジョーダン・ネットワーク（1986年）とエルマン・ネットワーク（1990年）という2つの研究は、リカレントニューラルネットワーク（RNN）を認知心理学の応用することに貢献した。

1980年代、誤差逆伝播法（バックプロパゲーション）は深いリカレントニューラルネットワーク（RNN）に対してうまく機能しなかった。この問題を克服するために、1991年、ユルゲン・シュミットフーバーは「ニューラルシーケンスチャンカー」または「ニューラルヒストリーコンプレッサー」を提案し、自己教師あり事前学習（ChatGPTの「P：Pre-trained」）と知識蒸留の重要な概念を導入した。1993年、ニューラルヒストリーコンプレッサーは、時間展開されたリカレントニューラルネットワーク（RNN）で1000以上の後続層を必要とする「超深層学習」タスクを解決した。

1991年、ゼップ・ホフレイターの論文では、勾配消失問題を特定して分析し、それを解決するために再帰的な残差接続を提案した。彼とシュミットフーバーは、複数の応用領域で精度の記録を打ち立てた長・短期記憶（LSTM）を導入した。これはまだ現代版のLSTMではなく忘却機能が必要とされた。これらの技術はRNNアーキテクチャのデフォルトとなった。

1985年から1995年の間、統計力学の影響で、テリー・セジュノウスキー、ピーター・デイアン、ジェフリー・ヒントンらによって、ボルツマンマシン、制限付きボルツマンマシン、ヘルムホルツマシン、およびウェイク-スリープアルゴリズムなど、いくつかのアーキテクチャと手法が開発された。これらは深層生成モデルの教師なし学習のために設計された。

ディープラーニングの登場

2006年、ジェフリー・ヒントンらによりオートエンコーダおよびディープ・ビリーフ・ネットワークが提案された。オートエンコーダは、ニューラルネットにおいて、入力層と出力層に同じデータを用いて教師なし学習させたものである。もともとは、次元削減や特徴抽出といった小さい次元に落とし込む作業を効率的に行うために開発された。実用上では、入力と出力の差分をとることで、異常検知に利用されている。

2009年から2012年にかけて、人工ニューラルネットワークは画像認識コンテストで賞を獲得し始め、さまざまなタスクで人間レベルのパフォーマンスに近づき、当初はパターン認識と手書き文字認識で成果を上げた。

2011年、ダン・シレサン、ウエリ・マイヤー、ジョナサン・マッシ、ルカ・マリア・ガンバルデッラ、ユルゲン・シュミットフーバーによるCNN「DanNet」は、視覚パターン認識コンテストで初めて超人的なパフォーマンスを達成し、従来の方法を3倍上回った。その後、さらに多くのコンテストで優勝した。彼らはまた、GPU上のマックスプーリングCNNがパフォーマンスを大幅に向上させることを示した。 2012年10月、アレックス・クリジェフスキー、イリヤ・サツケバー、ジェフリー・ヒントンによるAlexNetは、ImageNetが開催する大規模な画像認識技術コンテストILSVRC(the ImageNet Large Scale Visual Recognition Challenge)で、既存の機械学習手法に大差をつけて勝利した。さらに、カレン・シモニャンとアンドリュー・ジサーマンによるVGG-16ネットワークやGoogleのInceptionv3が開発され飛躍的に性能が向上した。

2012年、アンドリュー・ンとジェフ・ディーンは、ラベルのない画像を見るだけで、猫などの高レベルの概念を認識することを学習するネットワークを作成した。教師なし事前学習と、GPUおよび分散コンピューティングによる計算能力の向上により、特に画像および視覚認識の問題でより大規模なネットワークを使用できるようになり、これが「ディープラーニング」として知られるようになった。

2013年、動径基底関数ネットワークとウェーブレットネットワークが導入された。これらは最良の近似特性を提供することが示されており、非線形システム同定および分類アプリケーションで適用されている。

2014年、敵対的生成ネットワーク（GAN）（イアン・グッドフェローら、2014年）が導入され、2014年から2018年の期間に生成モデリングの最先端となった。GANの原理はもともと1991年にユルゲン・シュミットフーバーによって発表され、「人工的好奇心」と呼ばれた。2つのニューラルネットワークがゼロサムゲームの形で互いに競い合い、一方のネットワークの利得がもう一方のネットワークの損失となる。最初のネットワークは、出力パターンに対する確率分布をモデル化する生成モデルである。2番目のネットワークは、勾配降下法によって、これらのパターンに対する環境の反応を予測することを学習する。優れた画質は、テロ・カラスらによるプログレッシブGANに基づいたNvidiaのStyleGAN（2018年）によって達成される。ここでは、GANジェネレータはピラミッド方式で小規模から大規模に成長させられる。GANによる画像生成は広く成功を収め、ディープフェイクに関する議論を引き起こした。

2015年、拡散モデルが発表された。拡散モデルは、DALL-E 2（2022年）やStable Diffusion（2022年）に用いられGANを凌駕した。 当時、20～30層の「超深層ニューラルネットワーク」を訓練する必要があったが、あまりにも多くの層を重ねると、訓練精度が急激に低下する、いわゆる「劣化」問題が発生した。

2015年、それらの問題を解決するために、超深層ネットワークを訓練するために、2015年5月にハイウェイネットワークが発表され、2015年12月に残差ニューラルネットワーク（ResNet）が発表された。

アテンションメカニズムの導入

2014年頃、GoogleによりSeq2Seqが開発され、アテンションメカニズムが追加された。Seq2Seqは、情報理論のエンコード・デコードの考え方を機械翻訳に応用したもので、2014年に発表された2つの論文をもとに開発された。。具体的には、エンコーダーと呼ばれるニューラルネットワークが入力シーケンス（文章など）を固定長の数値ベクトルに変換し、デコーダーと呼ばれる別のニューラルネットワークがそのベクトルから出力シーケンスを生成する。当初のモデルでは、エンコーダーとデコーダーの両方にLSTMが使用されていた。このseq2seqには主に2つの問題点があった。一つ目は、ボトルネック問題と呼ばれる問題であり、入力情報を固定長のベクトルに圧縮するため、長い文章では情報が失われやすいという問題があった。二つ目は、リカレントニューラルネットワーク（RNN）をベースにしているため、計算の並列化が難しく、処理に時間がかかるという問題があった。

2017年に発表された論文、「Attention Is All You Need」により、seq2seqが抱えている問題を解決した。これが現代のTransformerにつながった。1992年に発表されたユルゲン・シュミットフーバーの「高速重みコントローラー」は線形にスケールし、後に非正規化線形Transformerと等価であることが示された。 Transformerは、自然言語処理のモデルとしてますます選択されるようになっている。ChatGPT、GPT-4、BERTなど、多くの現代の大規模言語モデルがこのアーキテクチャを使用している。

年表

• 1943年 - ウォーレン・マカロックとウォルター・ピッツが形式ニューロンを発表した。
• 1956年 - ダートマス会議より第1次AIブームが発生する。
• 1958年 - フランク・ローゼンブラットがパーセプトロンを発表した。単純パーセプトロンの学習方法を発表した。
• 1960年 - バーナード・ヴィドローとマーシャン・ホフが損失関数が二乗誤差損失の形式ニューロン（活性化関数が符号関数の単純パーセプトロン）を、内側のアフィン変換 Wx + b の部分を確率的勾配降下法で学習させた。
• 1964年 - R.E. Wengertが自動微分を発表した。最初に提案した人は不明であるが、バックプロパゲーションと同じく、自動微分にて出力側から偏微分する方法が1960年代後半には提案されていた。
• 1967年 - 甘利俊一が多層パーセプトロンを確率的勾配降下法で学習した。線形分離不可能なパターンが学習できることを書籍『情報理論II ―情報の幾何学的理論―』のp.119で例示した。
• 1969年 - マービン・ミンスキーとシーモア・パパートが著書『パーセプトロン』の中で、単純パーセプトロンは線形分離不可能なパターンを識別できない事を示した。
• 1979年 - 福島邦彦がネオコグニトロンを発表し、文字認識に使用し、後にこれが畳み込みニューラルネットワークへと発展する。
• 1982年 - ジョン・ホップフィールドによってホップフィールド・ネットワーク（再帰型ニューラルネットワーク）が提案された。
• 1984年 - ジェフリー・ヒントンらによりボルツマンマシンが提案された。
• 1986年 - デビッド・ラメルハート、ジェフリー・ヒントンらにより出力側から偏微分する方法がバックプロパゲーション（誤差逆伝播法）と命名された。論文では最急降下法を使用していたのだが、確率的勾配降下法が学習方法として定着した。第2次AIブームが発生する。
• 1988年 - 畳み込みニューラルネットワークを本間俊光らが音素の認識に、1989年にヤン・ルカンらが文字の認識に使用した。畳み込みニューラルネットワークはディープラーニングの一種に分類される。
• 2006年 - ジェフリー・ヒントンらによりオートエンコーダおよびディープ・ビリーフ・ネットワークが提案される。
• 2012年 - ジェフリー・ヒントンの研究室の畳み込みニューラルネットワークを用いた画像認識システムAlexNetがImageNet Large Scale Visual Recognition Challengeで優勝する。第3次AIブームが発生する。
• 2017年 - Transformerが発表され、大規模言語モデルで使用される。

代表的な人工ニューラルネットワーク

順伝播型ニューラルネットワーク

順伝播型ニューラルネットワーク（フィードフォワードニューラルネットワーク、英: Feed-forward Neural Network; FFN, FFNN）は内部に循環を持たないニューラルネットワークの総称・クラスである。

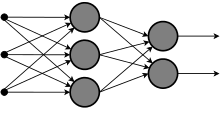
ニューラルネットワークではしばしば層（レイヤ）の概念を取り入れる。FFNでは入力レイヤ→中間レイヤ→出力レイヤというように単一方向/順方向へのみ信号が伝播する。これは回帰型ニューラルネットワークと対比される。層間の結合様式により様々なニューラルネットワークが存在するが、結合様式に関わらず回帰結合を持たないものはすべてFFNに属する。以下はFFNの一例である。

• 単純パーセプトロン: 1-layer 層間全結合ネットワーク
• 多層パーセプトロン: N-layer 層間全結合ネットワーク
• 畳み込みニューラルネットワーク: N-layer 層間局所結合ネットワーク（c.f. recurrent CNN; RCNN）

並列計算

FFNがもつ特徴に並列計算がある。回帰結合をもつネットワークはシーケンシャルに処理を繰り返す必要があるため、1データに対して時間方向に並列計算できない。FFNは層内で並列計算が可能であり、RNNと比較して容易に並列計算機（例: GPU）の計算能力を上限まで引き出せる。

多層パーセプトロンの模式図

RBFネットワーク

誤差逆伝播法に用いられる活性化関数に放射基底関数を用いたニューラルネットワーク

• RBFネットワーク
• 一般回帰ニューラルネットワーク（GRNN、General Regression Neural Network）- 正規化したRBFネットワーク

自己組織化写像

自己組織化写像はコホネンが1982年に提案した教師なし学習モデルであり、多次元データのクラスタリング、可視化などに用いられる。自己組織化マップ、コホネンマップとも呼ばれる。

• 自己組織化写像
• 学習ベクトル量子化

畳み込みニューラルネットワーク

畳み込みニューラルネットワーク

畳み込みニューラルネットワークとは層間が全結合ではない順伝播型ニューラルネットワークの一種。画像を対象とするために用いられることが多い。

再帰型ニューラルネットワーク（リカレントニューラルネット、フィードバックニューラルネット）

→「回帰型ニューラルネットワーク」も参照

フィードフォワードニューラルネットと違い、双方向に信号が伝播するモデル。すべてのノードが他の全てのノードと結合を持っている場合、全結合リカレントニューラルネットと呼ぶ。シーケンシャルなデータに対して有効で、自然言語処理や音声、動画の解析などに利用される。

• ホップフィールド・ネットワーク

Transformer

→「Transformer (機械学習モデル)」も参照

Self-Attention機構（自己注意機構）を利用したモデルである。再帰型ニューラルネットワークの代替として考案された。

従来の自然言語処理用モデルに比べ計算量が少なく構造も単純なため、自然言語処理に使われることが多い。

確率的ニューラルネット

乱数による確率的な動作を導入した人工ニューラルネットワークモデル。モンテカルロ法のような統計的標本抽出手法と考えることができる。

• ボルツマンマシン
• ベイジアンネットワーク

スパイキングニューラルネットワーク

ニューラルネットワークをより生物学的な脳の働きに近づけるため、活動電位（スパイク）を重視して作られた人工ニューラルネットワークモデル。スパイクが発生するタイミングを情報と考える。ディープラーニングよりも扱える問題の範囲が広い次世代技術と言われている。ニューラルネットワークの処理は逐次処理のノイマン型コンピュータでは処理効率が低く、活動電位まで模倣する場合には処理効率がさらに低下するため、実用する際には専用プロセッサとして実装される場合が多い。

2015年現在、スパイキングNN処理ユニットを積んだコンシューマー向けのチップとしては、QualcommのSnapdragon 820が登場する予定となっている。

複素ニューラルネットワーク

入出力信号やパラメータ（重み、閾値）が複素数値であるようなニューラルネットワークで活性化関数は必然的に複素関数になる。

利点

情報の表現

入力信号と出力信号が複素数（2次元）であるため、複素数で表現された信号はもとより、2次元情報を自然に表現可能。また特に波動情報（複素振幅）を扱うのに適した汎化能力（回転と拡大縮小）を持ち、エレクトロニクスや量子計算の分野に好適である。四元数ニューラルネットワークは3次元の回転の扱いに優れるなど、高次複素数ニューラルネットワークの利用も進む。

学習特性

階層型の複素ニューラルネットワークの学習速度は、実ニューラルネットワークに比べて2〜3倍速く、しかも必要とするパラメータ（重みと閾値）の総数が約半分で済む。学習結果は波動情報（複素振幅）を表現することに整合する汎化特性を示す。

生成モデル/統計モデル

生成モデル（統計モデルとも）は、データが母集団の確率分布に従って生成されると仮定しそのパラメータを学習するニューラルネットワークの総称である。統計的機械学習の一種といえる。モデル（＝母集団）からのサンプリングによりデータ生成が可能な点が特徴である（詳しくは推計統計学 § 統計モデル、機械学習 § 統計的機械学習）。

自己回帰型生成ネット

$series\sim p(x_{t},x_{t-1},...,t_{0})=\prod _{i=0}^{N}p(x_{t}|x_{<t})=\prod _{i=0}^{N}NeuralNetwork(x_{t}|x_{<t})$

自己回帰型生成ネット（Autoregressive Generative Network）とは、系列データの生成過程（同時確率分布）を系列の過去データに対する条件付分布の積と考え条件付分布をニューラルネットワークで表現するモデルである。非線形自己回帰生成モデルの一種、詳しくは自己回帰モデル § 非線形自己回帰生成モデル。画像生成におけるPixelCNN、音声生成におけるWaveNet・WaveRNNがその例である。学習時は学習データを条件付け（=入力）にできるため、ニューラルネットワーク自体が再帰性を持っていなければ並列学習が容易である（CNN型のWaveNetなど）。ニューラルネットワーク自体に再帰性がある場合は学習時も系列に沿った逐次計算が必要となる（RNN型のWaveRNNなど）。

変分オートエンコーダ

変分オートエンコーダ (VAE) とは、ネットワークA（エンコーダ）が確率分布のパラメータを出力し、ネットワークＢ（デコーダ）が確率分布から得られた表現をデータへと変換するモデルである。画像・音楽生成におけるVQ-VAE-2がその例である。

敵対的生成ネットワーク

敵対的生成ネットワーク (Generative Adversarial Network, GAN) とは、ガウシアン等の確率分布から得られたノイズをネットワークA (Generator) がデータへ変換し、ネットワークBが母集団からサンプリングされたデータとネットワークＡの出力を見分けるように学習するモデルである。DCGANやStyleGAN、BigGANがその例である。

flow-based生成モデル

flow-based生成モデルはFlow、Glow、NICE、realNVP等が存在する。

Graph neural networks (GNN)

グラフを入力とするニューラル・ネットワークである。

構成要素

ニューラルネットワークは様々な要素を組み合わせからなる。各構成要素は経験的・理論的に示された特徴をニューラルネットワークへもたらしている。

Table. ニューラルネットワークの構成要素

総称/名称		概念	意図/効果	例
skip connection		x = x + f(x)	勾配消失の防止	ResNet
			アンサンブル学習	ResNet
			位置情報の保持	U-Net
ボトルネック構造		Wshallow > Wmiddle < Wdeep	特徴抽出	AE
			圧縮された潜在表現	generative AE
階層構造		middle(x) = f(x + bottom(x))	局所/全体特徴の両立	U-Net GAN
一貫性 consistency	cycle	GB2A(GA2B(a)) = a	コンテンツ/不変特徴の保持	CycleGAN
	latent	D(G(z)) = D(G(z+Δ))	潜在変数ゆらぎへの堅牢性	ICR-BigGAN
	データ拡張	D(Aug(x)) = D(x) D(G(z)) = D(Aug(G(z)))	leakのないデータ拡張	CR-GAN ICR-BigGAN
progressive	output	Size(Gt=0(x)) < Size(Gt=1(x))	学習の高速化・安定化	PGGAN
	input	Input Complexity t0 < t1	学習の高速化・安定化	PA-GAN
正規化	batch	y = γc Norm(x) + βc	学習の高速化
	layer
	instance
	group
	Conditional	y = γcnl,s Norm(c) + βcnl,s	スタイル変換
	AdaIN	y = σ(s) Norm(c) + μ(s)	スタイル変換	StyleGAN
	SPADE		スタイル変換

バッチ正規化

バッチ正規化（英: Batch Normalization）は学習時のミニバッチに対する正規化である。バッチ正規化レイヤー/BNでは学習時にバッチ内統計量（平均μ, 分散σ）を計算し、この統計量により各データを正規化する。その上で学習可能パラメータ (β, γ) を用いて y = γX+βの線形変換をおこなう。これにより値を一定のバラツキに押し込めた上で柔軟に線形変換することができる。

CNNの場合、各チャネルごとにバッチ正規化処理がおこなわれる。バッチ方向ではない正規化手法も様々提案されており、Layer Norm・Instance Norm・Group Normなどがある。また正規化時のβ・γを計算から求めたりNN(β)・NN(γ)で表現する手法も存在する。

活性化関数

→詳細は「活性化関数」を参照

ニューラルネットワークにおいて、各人工神経は線形変換を施した後、非線形関数を通すが、これを活性化関数という。シグモイド関数やReLUなど様々な種類があり、詳細は活性化関数を参照。

学習

ニューラルネットワークの学習は、損失関数を最小化する最適化問題である。現在は確率的勾配降下法が最もよく用いられている。確率的勾配降下法の計算方法は AdaGrad, AdaDelta, Adam など様々な変種が作られている。詳細は確率的勾配降下法を参照。

偏微分の計算方法

→「バックプロパゲーション」も参照

確率的勾配降下法を使用するには、損失関数のパラメータに関する偏微分を計算する必要がある。その際、出力側から偏微分を計算すると効率よく計算できる。この手法は1986年にバックプロパゲーションと命名された。1960年代に開発された自動微分のトップダウン型（リバース・モード）と同一の手法であり、現在では、手作業で式変形をするのではなく自動微分が通常は使われる。手作業で式変形する方法はバックプロパゲーションを参照。入力側よりも出力側から偏微分を計算すると計算効率が良いのは損失関数の出力がスカラーだからであり、詳細は自動微分を参照。

勾配法以外の学習方法

1986年のバックプロパゲーション命名以前は、勾配法以外の学習方法(gradient-free method)が主に使われていて、様々な方法が提案されてきて、現在でも研究が進められている。

確率的勾配降下法のテクニック

確率的勾配降下法を用いて（深層）ニューラルネットワークモデルを素早く・最適解へ収束させるために様々なテクニックが提唱されている。

標準的なテクニックをヤン・ルカンらが1998年にまとめていて、2010年に Xavier Glorot らが追証・発展させている。以下に要約する。詳細はそれぞれの論文を参照。

• オンライン学習において訓練データが一周したら毎回シャッフルし直す
• 入力は、平均を0にし、主成分分析により線形相関を取り除き、分散が1になるように線形変換する。面倒だったら主成分分析は省略しても良い。
• 目標値（出力）は活性化関数を通す場合は、二次導関数が最大になる範囲内を使用するべきである。$1.7159\tanh(2x/3)$ の場合は −1〜1 で、tanh(x) の場合は $-0.5\cosh ^{-1}(2)$ 〜 $0.5\cosh ^{-1}(2)$ = −0.65848 〜 0.65848 である。
• 初期値: 各層で平均0分散1、かつ連続一様分布
  • 入力ベース: $U(-{\sqrt {3/{{\text{fan}}_{\text{in}}}}},{\sqrt {3/{{\text{fan}}_{\text{in}}}}})$ by ヤン・ルカン
  • 入出力ベース: $U(-{\sqrt {6/{{\text{fan}}_{\text{in}}+{\text{fan}}_{\text{out}}}}},{\sqrt {6/{{\text{fan}}_{\text{in}}+{\text{fan}}_{\text{out}}}}})$ by Xavier Glorot
• 勾配法: 様々なパラメータ更新法が提案され利用されている（確率的勾配降下法#変種を参考）。
• 活性化関数
  • 原点を通過すなわち $f(0)=0$
    • 例:$\tanh(x)$、${\frac {x}{1+|x|}}$、逆に標準シグモイド関数は f(0) = 0.5 のため不適切
  • 入出力範囲 $f(\pm 1)=\pm 1$
    • 例: $1.7159\tanh(2x/3)$
  • ReLU（ランプ関数、アナログ閾素子（英: analog threshold element））: 経験的に良い性能

確率的勾配降下法の限界

• 損失超平面が極小値 (英: local minima) を持ちうるため、勾配法では広域最適解 (英: global minima) に収束する保証がない (Remelhart, 1986)
• 一カ所でも勾配消失を起こすとそれより下層は学習が進まなくなるため、層数が増えるほど勾配消失を起こす確率が増大していく
• 勾配が0に近い部分が存在する活性化関数を使っていると勾配消失を起こしやすい
• 学習が必ず収束するとは限らない
• 各次元の分散に差がありすぎると分散の小さいところに重みが集中しやすい

推論

ニューラルネットワークの学習と対比して、学習したニューラルネットワークで出力を計算することは推論（英: inference）と呼ばれる。

実装

ニューラルネットワークは「アフィン変換 + 非線形活性化関数; $y=\sigma ({\boldsymbol {w}}{\boldsymbol {x}}+{\boldsymbol {b}})$」を基本単位とするため、実装の基礎はドット積ひいては積和演算になる。またレイヤー概念によりスカラ出力を束ねた出力ベクトルとなり（${\boldsymbol {y}}=\sigma (W{\boldsymbol {x}}+{\boldsymbol {b}})$）、Level 2 BLAS すなわち行列ベクトル積が基礎となる。入力のバッチ化は入出力の行列化と同義であり（$Y=\sigma (WX+B)$）、Level 3 BLAS すなわち行列積が基礎となる。

ハードウェアアクセラレーション

ニューラルネットワークの学習と推論を高速化する様々なハードウェアアクセラレーションAPIが提案・実装されている。NVIDIAのcuDNNやIntelのoneDNNなどが挙げられる。

GPU

行列の掛け算はGPGPUが得意としており、高速に計算できる。PythonではPyTorchやTensorFlowなどのライブラリおよびそれを間接的に使用してる機械学習のライブラリなどがある。

CPUによる並列化

CPUのメニーコアやSIMDを有効活用する簡単な方法は行列演算ライブラリを使用する方法である。行列演算ライブラリとしては、例えばインテルのCPU向けではIntel Math Kernel Libraryなどがある。

バックプロパゲーションは完了までに非常に時間のかかる反復処理である。マルチコアのコンピュータでマルチスレッド技法を使えば、収斂までにかかる時間を大幅に短縮することができる。バッチ学習を行う場合、マルチスレッドでバックプロパゲーションのアルゴリズムを実行するのが比較的簡単である。

訓練データをそれぞれのスレッド毎に同程度の大きさに分割して割り当てる。それぞれのスレッドで順方向と逆方向のプロパゲーションを行う。重みとしきい値のデルタをスレッド毎に合計していく。反復の周回毎に全スレッドを一時停止させて、重みとしきい値のデルタを合計し、ニューラルネットワークに適用する。これを反復毎に繰り返す。このようなバックプロパゲーションのマルチスレッド技法がEncog Neural Network Frameworkで使われている。

量子化

量子化（英: quantization）はニューラルネットワークの重み（weight）および演算入出力（activation）の数値表現精度を下げる最適化である。例えば8-bit量子化では通常FP32で表現される数値をINT8で表現する。

量子化の効果は以下の要素から生み出される。

• プロセッサ命令: FP32より高効率なINT8命令の利用（例:IPC、1命令あたりの演算数（AVX-FP32: 8要素、AVX2-INT8: 32要素））
• キャッシュ: 容量低下によるキャッシュへ乗るデータ量増加 → キャッシュヒット率向上
• メモリ: 容量低下によるメモリ消費とメモリ転送量の減少
• 数値精度: 計算精度の低下によるモデル出力精度の低下
• 計算量: 量子化-脱量子化の導入による計算量の増加

量子化が最終的にメリットをもたらすかは上記の要素の組み合わせで決定される。効率的な命令セットを持たない場合、出力精度が下がりさらにQDQの計算負荷が勝って速度が悪化する場合もある。このように、量子化の効果はモデルとハードウェアに依存する。

量子化手法にはいくつかのバリエーションがある。

• 静的量子化（英: Static Quantization）: 代表的データを用いた量子化パラメータの事前算出
• 動的量子化（英: Dynamic Quantization）: 各実行ステップのactivation値に基づくactivation用量子化パラメータの動的な算出（weightは実行前に量子化）
• fake quantization (Quantize and DeQuantize; QDQ): 量子化+脱量子化（$y=dequant(quant(x))$）。学習時の量子化模倣あるいは量子化オペレータの表現

スパース化

スパース化（英: sparsification）はニューラルネットワークの重みを疎行列とする最適化である。スパース化は精度の低下と速度の向上をもたらす。

スパース化の効果は以下の要素から生み出される。

• キャッシュ: 容量低下によるキャッシュへ乗るデータ量増加 → キャッシュヒット率向上
• メモリ: 容量低下によるメモリ消費とメモリ転送量の減少
• 数値精度: 小さい値のゼロ近似によるモデル出力精度の低下
• 計算量: ゼロ重みとの積省略による計算量の減少

スパース化の恩恵を受けるためにはそのためのフォーマットや演算が必要になる。ゼロ要素を省略する疎行列形式、疎行列形式に対応した演算実装などが挙げられる。またスパース化を前提として精度低下を防ぐよう学習する手法が存在する。

より広い意味での重み除去は枝刈り（英: pruning）と呼ばれる。枝刈りでは行列のスパース化のみでなく、チャネルやモジュール自体の削除（ゼロ近似）を含む。

実装例

ここでは、2層の多層パーセプトロンで回帰を実装する。$x=[-1,1]$ において、$y=2x^{2}-1$ を学習する。活性化関数はReLUを使用。学習は、確率的勾配降下法でバックプロパゲーションを行う。

2層の多層パーセプトロンのモデルの数式は以下の通り。X が入力、Y が出力、T が訓練データで全て数式では縦ベクトル。$\psi$ は活性化関数。$W_{1},W_{2},B_{1},B_{2}$ が学習対象。$B_{1},B_{2}$ はバイアス項。

$Y=W_{2}\psi (W_{1}X+B_{1})+B_{2}$

誤差関数は以下の通り。誤差関数は出力と訓練データの間の二乗和誤差を使用。

$E={\frac {1}{2}}\|Y-T\|^{2}$

誤差関数 $E$ をパラメータで偏微分した数式は以下の通り。肩についてる T は転置行列。$\circ$ はアダマール積。

${\begin{aligned}{\frac {\partial E}{\partial W_{1}}}&=\left(\left((Y-T)^{\mathrm {T} }W_{2}\right)^{\mathrm {T} }\circ \psi '(W_{1}X+B_{1})\right)X^{\mathrm {T} }\\{\frac {\partial E}{\partial B_{1}}}&=\left((Y-T)^{\mathrm {T} }W_{2}\right)^{\mathrm {T} }\circ \psi '(W_{1}X+B_{1})\\{\frac {\partial E}{\partial W_{2}}}&=(Y-T)\psi (W_{1}X+B_{1})^{\mathrm {T} }\\{\frac {\partial E}{\partial B_{2}}}&=Y-T\end{aligned}}$

Python 3.5 によるソースコード。Python において、@ は行列の乗法の演算子、** は冪乗の演算子、行列同士の * はアダマール積。

import numpy as np

dim_in = 1              # 入力は1次元
dim_out = 1             # 出力は1次元
hidden_count = 1024     # 隠れ層のノードは1024個
learn_rate = 0.005      # 学習率

# 訓練データは x は -1～1、y は 2 * x ** 2 - 1
train_count = 64        # 訓練データ数
train_x = np.arange(-1, 1, 2 / train_count).reshape((train_count, dim_in))
train_y = np.array([2 * x ** 2 - 1 for x in train_x]).reshape((train_count, dim_out))

# 重みパラメータ。-0.5 〜 0.5 でランダムに初期化。この行列の値を学習する。
w1 = np.random.rand(hidden_count, dim_in) - 0.5
w2 = np.random.rand(dim_out, hidden_count) - 0.5
b1 = np.random.rand(hidden_count) - 0.5
b2 = np.random.rand(dim_out) - 0.5

# 活性化関数は ReLU
def activation(x):
    return np.maximum(0, x)

# 活性化関数の微分
def activation_dash(x):
    return (np.sign(x) + 1) / 2

# 順方向。学習結果の利用。
def forward(x):
    return w2 @ activation(w1 @ x + b1) + b2

# 逆方向。学習
def backward(x, diff):
    global w1, w2, b1, b2
    v1 = (diff @ w2) * activation_dash(w1 @ x + b1)
    v2 = activation(w1 @ x + b1)

    w1 -= learn_rate * np.outer(v1, x)  # outerは直積
    b1 -= learn_rate * v1
    w2 -= learn_rate * np.outer(diff, v2)
    b2 -= learn_rate * diff

# メイン処理
idxes = np.arange(train_count)          # idxes は 0～63
for epoc in range(1000):                # 1000エポック
    np.random.shuffle(idxes)            # 確率的勾配降下法のため、エポックごとにランダムにシャッフルする
    error = 0                           # 二乗和誤差
    for idx in idxes:
        y = forward(train_x[idx])       # 順方向で x から y を計算する
        diff = y - train_y[idx]         # 訓練データとの誤差
        error += diff ** 2              # 二乗和誤差に蓄積
        backward(train_x[idx], diff)    # 誤差を学習
    print(error.sum())                  # エポックごとに二乗和誤差を出力。徐々に減衰して0に近づく。

参考文献

• 上坂吉則『ニューロコンピューティングの数学的基礎』 近代科学社、1993年、ISBN 4-7649-0219-2。
• 斎藤康毅『ゼロから作るDeep Learning - Pythonで学ぶディープラーニングの理論と実装』 オライリージャパン、2016年（第1刷）、ISBN 978-4873117584。
• Vaswani, Ashish; Shazeer, Noam; Parmar, Niki; Uszkoreit, Jakob; Jones, Llion; Gomez, Aidan N.; Kaiser, Łukasz; Polosukhin, Illia (2017-12-04). “Attention is all you need”. Proceedings of the 31st International Conference on Neural Information Processing Systems (Red Hook, NY, USA: Curran Associates Inc.): 6000–6010. doi:10.5555/3295222.3295349. ISBN 978-1-5108-6096-4. https://dl.acm.org/doi/10.5555/3295222.3295349. 
• 山内康一郎『作って学ぶニューラルネットワーク ― 機械学習の基礎から追加学習まで』 コロナ社、2020年、ISBN 978-4-339-02911-6。

関連項目

• 人工知能
• 強化学習
• 機械学習
• ニューロコンピュータ
• コネクショニズム
• 認知科学
• ウォーレン・マカロック
• ウォルター・ピッツ
• ヘッブの法則
• 認知アーキテクチャ
• 階層構造
• 創発
• Neuroevolution
• コネクトーム
• ディープラーニング
• ヒトの脳
• 幹細胞
• 脳オルガノイド

外部リンク

• 『ニューラルネットワークモデル』 - コトバンク
• 『ニューラルネットワーク』 - コトバンク