指数表記
指数表記(しすうひょうき、英: exponential notation)、または科学的表記(scientific notation)[1]は、数の表記方法の1つである。非常に大きな数または非常に小さな数を表記するのに便利で、科学技術分野で多用される。
| 通常の表記 | 指数表記 |
|---|---|
| 2 | 2×100 |
| 300 | 3×102 |
| 4321.768 | 4.321768×103 |
| −53000 | −5.3×104 |
| 6720000000 | 6.72×109 |
| 0.2 | 2×10−1 |
| 987 | 9.87×102 |
| −0.00000000751 | −7.51×10−9 |
表記方法[編集]
任意の有理数を、次の形式で表現する[2]。負の数の場合は、先頭にマイナス符号を付ける。
- m × 10n
m は有理数、n は整数である。m を仮数部 (mantissa)、n を指数部 (exponent) と呼ぶ。
例えば、
- 6.02214076×1023 アボガドロ定数(単位: mol−1)
- 6.62607015×10−34 プランク定数 (単位: J s)
- −9.2847647043×10−24 電子の磁気モーメント(単位: J⋅T−1)
仮数部 (m) には通常有限小数を用い、小数部は3桁ごとにスペース(正確には thin space)を挟むのが通例である。ただし、小数点の後の数字列が4桁の場合やスペースの後の数字列が4桁の場合は、1桁だけ分けるためのスペースを挿入しないのが普通である[3][4]。
例えば、
- 7.2973525693×10−3 微細構造定数(無次元量)
E表記[編集]
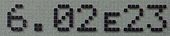
コンピュータにおける表記では、仮数部と指数部の間に記号"E"(大文字)または"e"(小文字)を挟む。この表記法はE表記(英: E notation)と呼ばれ、JIS X 0210-1986(情報交換用文字列による数値表現)[5]に規定されている。
- 例: -8.984E+8 または -8.984e+8 (= −8.984 × 108)
- 例: 1.234E-5 、 +1.234E-5 、1.234e-5 または +1.234e-5 (= 1.234 × 10−5)
(注)仮数が正数の場合は先頭の「+」は省略できる。指数が正数の場合は指数の前の「+」は省略できる[6]。
単位記号[編集]
指数表記の使用の拡張として、単位記号の表記にも用いられる[7]。例えば、
不確かさを含めた表記[編集]
計測値には数値の不確かさがあるので、その程度を含めた指数表記を用いることがある。例えば、
- 中性子の質量の表記: 1.67492749804(95)×10−27 kg
これは、(1.67492749804±0.00000000095)×10−27 kgを簡略に表記したものである(不確かさ (測定)#表記)。
正規化[編集]
指数表記において、仮数部 mを 1 ≦ m < 10 となるような表記にすることを正規化と呼ぶ(Normalized numberも参照)。次の例では、左辺を正規化したものが右辺である。
- 267.8948 × 1011 = 2.678 948 × 1013
1 ≦ m < 1000 となるように表記することもある。
- 1.716 742 × 1020 = 171.6742 × 1018 (指数を3の倍数となるようにする。)
正規形[編集]
JIS X 0210-1986(情報交換用文字列による数値表現)においては、上記のように正規化したものを「通常の表記法」としているのに対して、0.1 ≦ m < 1 となるような m を用いた表現を「正規形」と定義している[8]。
- 例:正規形 :+0.61902E+04
これは 0.61902×104、すなわち 6190.2 または 6.1902×103 と同一である。
使用[編集]
陽子の質量は、0.00000000000000000000000000167262192369 kg であり、電子の質量は、0.00000000000000000000000000000091093837015 kg である。このような通常の表記では、両者の質量の比較が非常にしにくい。これに対して、指数表記であれば、前者は 1.67262192369×10−27 kg であり、後者は 9.1093837015×10−31 kg となって比較が容易であり、また陽子の質量が電子のそれの約1836倍( 1.67262192369×10−27 kg / 9.1093837015×10−31 kg )であることも容易に計算できる。このため、科学技術分野においては数値の表記として指数表記が極めて頻繁に用いられる。
地球の質量は、5972000000000000000000000 kgである[9]。指数表記では、5.972×1024 kgとなる。
3の倍数の指数部[編集]
工学の分野では、指数部 n の値として、3, 6, 9, 12, 15, −3, −6, −9, −12 など 3 の倍数を用いることが多い。これはSI接頭語は103毎の倍数となっているものを使用することが推奨される(SI接頭語#使用法)ため、換算が容易であるからである。
- 3.3 × 107 Hz → 33 × 106 Hz = 33 MHz
- 0.009 52 g → 9.52 × 10−3 g = 9.52 mg
- 2703 W → 2.703 × 103 W = 2.703 kW
- 5.8 × 10−8 m → 58 × 10−9 m = 58 nm
指数表記にしない例[編集]
定義定数そのものを表記する場合は次の例のように、指数表記にしないことが多い。
- 例:光速度 299792458 m/s[11] (2.99792458×108 m/s とはしない。)
- 例:天文単位 (au) 149597870700 m[12] (1.49597870700×1011 m とはしない。)
リュードベリ定数のように、慣例的に指数表記にしない物理定数もある。
- 例:リュードベリ定数 10973731.568160 m−1[13]
- 例:フォン・クリッツィング定数 25812.80745... Ω [14]
日本の命数法の場合[編集]
日本語の命数法では、日常的に用いられる数の単位はおよそ兆までであり、その先にも京や垓などの単位があるが、京以上の数については指数表記を用いるのが普通である。例えば3162穣年なら3162×100007年などと表記する。
指数表記以外の表記[編集]
多くの現実的な目的においては、非常に大きな数を表すのに指数表記が一般的に用いられるが、モーザー数やグラハム数などのように、指数表記を用いるのが事実上不可能なほど超巨大な数を扱う場合には、超階乗やクヌースの矢印表記、 コンウェイのチェーン表記などが用いられる(巨大数#巨大数の表記法を参照)。
脚注[編集]
- ^ 数値の科学的表記 分析室の屋根裏、弘前大学、2021-01-29
- ^ 科学的表記法 (scientific notation) KIT物理ナビゲーション、金沢工業大学
- ^ 国際単位系(SI)第9版(2019)日本語版 産業技術総合研究所 計量標準総合センター、p.119
- ^ 実例として、国際単位系 (SI) 国際文書第8版(2006) 日本語版 p. 38 表7(SI単位で表される数値が実験的に求められる非SI単位)中、時間の自然単位、長さの原子単位.ボーア(ボーア半径)0.5291772108 (18)×10−10 m
- ^ JIS X0210-1986 情報交換用文字列による数値表現
- ^ JIS X0210-1986 情報交換用文字列による数値表現、7.1,7.2 、p.4
- ^ 国際単位系(SI)第9版(2019)日本語版 産業技術総合研究所 計量標準総合センター、p.116
- ^ JIS X0210-1986 情報交換用文字列による数値表現、7.5 、p.5
- ^ 理科年表2020年版 天文部 p.78
- ^ Guide for the Use of the International System of Units (SI), 2008 Edition 7.9 Choosing SI prefixes, pp.18-19, NIST
- ^ 光速度 CODATA 2014
- ^ 理科年表2020、p.377、2019年11月20日発行
- ^ [1] CODATA Value 2018
- ^ [2] CODATA Value 2018
関連項目[編集]
- 指数
- オーダー (物理学) - 正規化表現をしたときの、指数にのみ注目する。
- Parts-per表記 - ppm, ppb など
- 単位記号
- 計算尺 - 数値の読み取りに使う
- 有効数字
- 浮動小数点数
- 桁落ち、情報落ち - 表現精度が限られた指数表記に特有の誤差。
