万有引力定数

出典: フリー百科事典『ウィキペディア（Wikipedia）』
移動先: 案内、 検索
万有引力定数
NewtonsLawOfUniversalGravitation.svg
万有引力の法則における万有引力定数 G
記号 G
値 6.67408(31)×10−11 m3 kg−1 s−2 [1]
定義 重力相互作用の大きさを表す定数
相対標準不確かさ 4.7×10−5
テンプレートを表示

万有引力定数（ばんゆういんりょくていすう）あるいは（ニュートンの）重力定数（じゅうりょくていすう、英: (Newtonian) constant of gravitation）とは、重力相互作用の大きさを表す物理定数である。アイザック・ニュートンの万有引力の法則において導入された。記号は一般に G で表される。

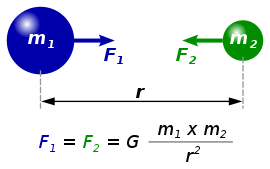
ニュートンの万有引力理論において、それぞれ m1、m2 の質量を持つ2つの物体が、距離 r だけ離れて存在しているとき、これらの間に働く万有引力 Fg は

となる。このときの比例係数 G が万有引力定数である。SIに基づいて、質量 m1、m2 にキログラム（kg）、長さ r にメートル（m）、力 Fg にニュートン（N、これは kg m s−2 に等しい）を用いれば、万有引力定数 G の単位は m3 kg−1 s−2 となる。

アインシュタインの一般相対性理論においては、ニュートンの重力理論に対する修正と拡張が為され、一般相対性理論の基礎方程式であるアインシュタイン方程式においても比例係数としてこの重力定数が現れる。

値[編集]

万有引力定数の2014年CODATA推奨値は

G = 6.67408(31)×10−11 m3 kg−1 s−2

である[1]。括弧内の数値は表された最後の桁を単位とした数値の標準不確かさを表す。上記の定数は、質量 1 kg の2つの質点が 1 m 離れた時の引力を単位ニュートン (N) で表した値と等しく、非常に小さい値である。たとえばそれぞれの重心が互いに 1 m 離れた1トン (=1000 kg) の物体が引き合う力は約 6.7×10−5 N であり、地球上で おおよそ 6.8 mg の質量の物体に働く重力に等しい。

また、万有引力定数をプランク定数と真空の光速で換算した量は

G/ħc =6.70861(31)×10−39 (GeV⁄c2)−2

である[2]。

キャヴェンディッシュによる測定[編集]

万有引力定数を定めるには、互いに質量のわかっているものの間に働く万有引力を精密に測定せねばならない。万有引力定数はキャヴェンディッシュによる1798年の鉛球実験（キャヴェンディッシュの実験）に基づいて初めて計測された。これは針金で吊るした棒の両端に二つの鉛球をつけ、固定した別の鉛球との間に働く力を計測するものであった。この実験はもともと地球の密度を求めるためのものとして考案されたもので、万有引力定数が求められたことによって、既知の重力加速度と地球の半径から地球の質量そして密度がはじめて求められた。この実験で求められた万有引力定数は 6.74×10−11 m3 kg−1 s−2 であり、現在知られている上記の値と比較しても相当に高精度なものであった。

精度の低さ[編集]

万有引力は非常に弱い力であるとともに、負の質量が存在しないために静電遮蔽のような効果を用いることができず、周囲の物質による影響が除去しにくいために測定が非常に難しい。上に示したCODATA2014の値にも、4.7×10−5 の標準不確かさがある。この不確かさは、様々な重要な物理定数の中では最も大きい[3][4][5]。

このような測定精度の低さのためCODATA推奨値も時代と共に以下のように変遷している[6]。CODATA2014推奨値とCODATA2010推奨値との差は、3.6×10−5 もあり[注 1]、基礎物理定数としては変化が極めて著しい。

万有引力定数のCODATA推奨値の変遷[7]
推奨値 G / m3kg−1s−2 標準不確かさ
1973 CODATA[8] 6.6720(41)×10−11 6.1×10−4
1986 CODATA 6.672 59(85)×10−11 1.3×10−4
1998 CODATA 6.673(10)×10−11 1.5×10−3
2002 CODATA 6.6742(10)×10−11 1.5×10−4
2006 CODATA 6.674 28(67)×10−11 1.0×10−4
2010 CODATA 6.673 84(80)×10−11 1.2×10−4
2014 CODATA 6.674 08(31)×10−11 4.7×10−5

万有引力定数の精度が4桁程度しかないことは、連星パルサーの質量の測定精度などにも影響する。また、ミリメートル以下の範囲でニュートンの万有引力が精度良く確かめられていないことから、小さなスケールでは重力理論の変更を考慮する余地が残されていて、近年、小さなスケールで余剰次元を持つ5次元膜宇宙モデル（ブレーンワールドモデル）が盛んに研究されている。

その他の値[編集]

国際測地学協会では1999年に万有引力定数の値として G = 6.67259(30)×10−11 m3 s−2 kg−1 を用いることを定めている[9]。NASAでもこの値を採用している[10]。

2007年には原子干渉計を用いた測定による万有引力定数として、G = 6.693(21)×10−11 m3 s−2 kg−1 というそれまでの測定結果とは著しく異なった値がサイエンスに報告された[11]。

天体の質量との積[編集]

万有引力定数の測定精度が低いのに対し、G に太陽質量 MS を乗じた日心重力定数（英語版）や、地球質量 ME を乗じた地心重力定数は精度よく計測されている。 これらの値は各々、

GMS = 1.32712442099(100)×1020 m3 s−2

GME = 3.986004418(8)×1014 m3 s−2

である[12]。

従って、地球質量の精度は万有引力定数の測定精度に依存し、CODATA 2006による地球質量は ME = 5.9722(6)×1024 kg と計算され[12]、国際測地学協会の協定値では ME = 5.9737(3)×1024 kg と計算される。NASAでは ME = 5.9736×1024 kg としている[13]。

一般相対性理論とアインシュタインの重力定数[編集]

アルベルト・アインシュタインの一般相対性理論においては、重力場を記述するアインシュタイン方程式の中に万有引力定数 G が現れる。アインシュタイン方程式は

と表される。左辺の Gμν は時空の曲率を表したアインシュタイン・テンソルと呼ばれるテンソルであり、Λ は「宇宙定数」と呼ばれる定数で、gμν は時空の計量テンソルと呼ばれるテンソルである。また、右辺の Tμν は物質分布を示すエネルギー・運動量テンソルであり、右辺の係数をまとめた κ = 8πG/c4 は、アインシュタインの重力定数と呼ばれることもある。

なお、左辺の Gμν は、リッチテンソル Rμν とスカラー曲率 R 及び時空の計量テンソル gμν を用いると Gμν = Rμν - 1/2Rgμν とも表わされる。

脚注[編集]

[ヘルプ]

注釈[編集]

  1. ^ 導出の計算式は 6.674 08×10−11/6.673 84×10−11 - 1 = 3.596×10−5 ≒ 3.6×10−5 となる。

出典[編集]

  1. ^ a b CODATA Value
  2. ^ CODATA Value
  3. ^ 例えば、Mohr et al. (2012) p.1594, TABLE XLVIII.
  4. ^ Mohr et al. (2012) pp.1587-1591
  5. ^ Mohr et al. (2012) p.1583, FIG. 6.
  6. ^ "Older values of the constants"
  7. ^ 1982年から2010までの主な測定結果については、Mohr et al. (2012) p.1567, TABLE XVII. が参考になる。
  8. ^ Cohen and Taylor
  9. ^ 『理科年表2009』
  10. ^ "Astrodynamic Constants"
  11. ^ Fixler, Foster, McGuirk, and Kasevich
  12. ^ a b "Selected Astronomical Constants" ただし値は時刻系の違いに依存し、示された値は太陽系座標時（TCB、Barycentric Coordinate Time）を用いて表されたものである。
  13. ^ "Earth Fact Sheet"

参考文献[編集]

関連項目[編集]

外部リンク[編集]

「https://ja.wikipedia.org/w/index.php?title=万有引力定数&oldid=60600929」から取得