ノート:五度圏

「五度圏」が閉じない理由について

解決済み後続議論の#議論の仕切り直しにて合意形成済み--610CH-405（会話） 2019年7月14日 (日) 12:40 (UTC)

題記の件につき2019年5月5日 (日) 09:31の版で下記の記述を追加しました。

しかし、純正な完全五度の周波数比は 1：1.5 なので、これを12回繰り返すと 1.5¹²≒129.746337890625 となり、7オクターヴ上（2⁷＝128）との間にわずかな差がある。

しかし、Kagefumimaruさんから「文脈の混乱」を理由にリバートされました。記述に間違いはなく、理解を深める上で有効と考えます。諸氏のご意見を伺いたく。--Tamie（会話） 2019年5月5日 (日) 10:21 (UTC)

ここまでの議論は利用者‐会話:Kagefumimaru#「五度圏」の件の通りです。--Tamie（会話） 2019年5月5日 (日) 10:29 (UTC)

Wikipediaはその分野に専門でない人にもわかりやすく書いた方が良いと思います。私の案はこんな感じです。すいませんが編集しちゃいまいました。--Gruppetto（会話） 2019年5月5日 (日) 11:47 (UTC)

Gruppettoさんの案では何故「ピッチクラスは閉じた環を形成しない」のか読者にはさっぱりわかりませんし、「上述のように」といいつつ上では異名同音について何も述べていないので意味不明です。「ピッチクラスは閉じた環を形成しない」のはピタゴラス音律において「異名同音関係が利用できない」ためであることがここの説明の中心です。12の純正な完全五度と7オクターヴとの差といったことはピタゴラス音律についての知識を前提としたもので、五度圏の図からはそのような操作は自ずからは出てきません。--Kagefumimaru（会話） 2019年5月5日 (日) 13:44 (UTC)

文の構造からいえば、元の文面では「実際には純正な完全五度の連鎖から得られるピッチクラスは閉じた環を形成しない」という『事実の提示』を行い、次に「閉じた環とするには G♭ / F♯ のような異名同音関係を利用する必要があるが、純正な完全五度を連鎖させた場合は異名同音のあいだにピタゴラスコンマの差が生じる」というその『理由の説明』を行っています。これにたいして『事実の提示』の前にも「このため」で接続されるような『理由の説明』を入れては文脈が混乱することは必至です。--Kagefumimaru（会話） 2019年5月5日 (日) 14:11 (UTC)

Kagefumimaruさんの版こそ「異名同音の音高差＝ピタゴラスコンマ」という、一般の人にはあまり知られていない知識を前提とするもののように思います。--Gruppetto（会話） 2019年5月5日 (日) 14:02 (UTC)

元の説明文においてピタゴラスコンマについての知識は特に要求されてはいないはずです。たとえばピタゴラスコンマを「甲」や「乙」といった名称にしても文意は通るはずです。もちろんここに具体的な数値を入れてその導出方法を説明してもいいでしょう。しかしそれは「ピタゴラスコンマ」としておけばピタゴラスコンマで説明されます--Kagefumimaru（会話） 2019年5月5日 (日) 14:15 (UTC)

もし具体的な数値を示すことが必要であれば以下のような案を提示します。

「実際には純正な完全五度の連鎖から得られるピッチクラスは閉じた環を形成しない。閉じた環とするには G♭ / F♯ のような異名同音関係を利用する必要があるが、純正な完全五度を連鎖させた場合は異名同音のあいだに約23.46セントの差が生じる。この差はピタゴラスコンマと呼ばれる。」

--Kagefumimaru（会話） 2019年5月5日 (日) 14:45 (UTC)

現状のGruppettoさんによる『純正な完全五度の周波数比 1：1.5 を12回繰り返した 1.512≒129.746337890625 と、7オクターヴ上（27＝128）との間の差（ピタゴラスコンマ）が異名同音のあいだに生じる』も、どこからともなく「12の純正な完全五度と7オクターヴとの差」という操作が出てきて読者には意味不明でしょう。--Kagefumimaru（会話） 2019年5月5日 (日) 15:02 (UTC)

ではこうしました。一般の人への分かりやすさは必要です。リンク先のピタゴラスコンマも一般の人への分かりやすさに配慮が足りません。百科事典だから正しいことさえ書いてあれば良いというのも一理はありますが、一般の人への分かりやすさも私は多少は考慮したいです。「純正な完全五度の周波数比 1：1.5 を12回繰り返した 1.512≒129.746337890625 と、7オクターヴ上（2の7乗＝128）との間の差」というTamieさんの記述の方がピタゴラスコンマの記事よりずっと分かりやすいからです。--Gruppetto（会話） 2019年5月5日 (日) 15:04 (UTC)追記--Gruppetto（会話） 2019年5月5日 (日) 15:10 (UTC)

それのどこが一般の人へのわかりやすさが配慮されているのでしょうか、相変わらず「12の純正な完全五度と7オクターヴとの差」という操作が唐突に出てきて意味不明と思います。上述の私の文案の一般の読者への配慮にかけている点を具体的に指摘してください。--Kagefumimaru（会話） 2019年5月5日 (日) 15:12 (UTC)

随分と妥協してKagefumimaruさんの文案を取り入れました。Kagefumimaruさんはかなり頭の良い方なのだと思います。しかし、一般の方への分かりやすさはこのTamieさんの記述が優れていると感じます。--Gruppetto（会話） 2019年5月5日 (日) 15:21 (UTC)

ですから「12の純正な完全五度と7オクターヴとの差」という操作を唐突に持ち出しても一般の読者には理解できないのでこれでは駄目です。また円滑な議論のために編集する前に文案をノートに提示してください。--Kagefumimaru（会話） 2019年5月5日 (日) 15:26 (UTC)

いや、私は「12の純正な完全五度と7オクターヴとの差」という話がとても分かりやすく感じました。それが不適切と仰るなら、同じくらいの分かりやすさでその不適切さを説明していただけますと有難いです。--Gruppetto（会話） 2019年5月5日 (日) 15:31 (UTC)

「12の純正な完全五度と7オクターヴとの差」という操作の由来が予備知識のない読者には知ることが出来ません。--Kagefumimaru（会話） 2019年5月5日 (日) 15:36 (UTC)

では、純正な完全5度を基にした異名同音に音高差が生じる理由を、「ピタゴラスコンマ」という言葉を用いずになるべく簡潔に短く表現すると、どうなりますか？--Gruppetto（会話） 2019年5月5日 (日) 15:41 (UTC)

自然がそのように出来ているからです。--Kagefumimaru（会話） 2019年5月5日 (日) 15:43 (UTC)

それは「説明の放棄」ですね。「12の純正な完全五度と7オクターヴとの差」の方ががシンプルで適切です。だからこの表現を私は支持します。--Gruppetto（会話） 2019年5月5日 (日) 15:46 (UTC)

これが厳密な意味での説明です。何故光速度が不変なのかや円周率が超越数なのかといった質問と同質のものです。数値の算出方法は示せてもそれが何故なのかの説明にはなりません。そしてあなたは「12の純正な完全五度と7オクターヴとの差」という操作の由来が予備知識のない読者には知ることができないのに、なぜそれを適切な説明と信じるのか説明してください。--Kagefumimaru（会話） 2019年5月5日 (日) 15:48 (UTC)

「なんで空はあおいの？」「自然がそのように出来ているからです」これをやったらwikipediaは終わりですよ。--Gruppetto（会話） 2019年5月5日 (日) 15:56 (UTC)

空が青く見えるのは波長の短い青の光が大気中で拡散しやすい性質を持つからであると説明できます。3の冪乗と2の冪乗が一致しないといった事とは全く性質を異にすることで、たとえ話として不適切です。しかしなぜ波長の短い光が青く見えるのかということは同様に説明はできないでしょう--Kagefumimaru（会話） 2019年5月5日 (日) 16:07 (UTC)

議論中にすみません。まったくの門外漢です。12という数字は表を見れば１周する数とわかるので特に気にはなりませんでした。オクターブについてもリンクをたどっていけば理解が可能な範囲なのかなと思います（正直言うと「周波数比」あたりから何のことやらわからないので、わからない度合は同じくらいという印象です）。一番気になったのは、1:1.5という比率がピタゴラス音律のページで言うところの3:2と同じなのかなあという点なので、同じなのであれば表記をそろえていただけるとわかりやすいかなという感想です。お二人とも少し過熱されているようですので、少し間を置いてご検討いただければと思います。--Nano blocks（会話） 2019年5月5日 (日) 15:51 (UTC)

そこは2:3にしても論旨は同じなので2:3に合わせて良いと思います。--Gruppetto（会話） 2019年5月5日 (日) 15:56 (UTC)

とりあえずまとめますと、TamieさんとGruppettoさんが必要だと考える「12の純正な完全五度と7オクターヴとの差」という操作は私は説明に不要だと考えますし、なによりそのような操作が突然脈絡なく書かれても読者には理解し難いと思うため、私はその記述の追加を認められません。Gruppettoさんは「12の純正な完全五度と7オクターヴとの差」という操作の由来が予備知識のない読者には知ることができないという指摘に対して、これを正当化する説明を拒否しています。Tamieさんのこれら関する意見は今の所ありません。--Kagefumimaru（会話） 2019年5月5日 (日) 17:49 (UTC)

私はtamieさんと同じく、この記述は理解を深める上で有効と考えます。「『12の純正な完全五度と7オクターヴとの差』という操作の由来が予備知識のない読者には知ることができない」とKagefumimaruさんはお考えのようですが、私はそうは思いません。--Gruppetto（会話） 2019年5月5日 (日) 19:20 (UTC)

Gruppettoさんが書いてくださった案でわたしは納得ですが、ただ、「閉じた環とするには G♭ / F♯ のような異名同音関係を利用する必要があるが、」という部分も、なぜそうすれば環が閉じるのかという具体的説明が何もないので、読む人にほんとうにわかるのか疑問です。この部分は削除した方が「閉じない」ことのずっと単純明快な説明になると思います。閉じさせるための話は、最後に平均律が出てくるのですから、それだけでよいのではないでしょうか。ただ、平均律の話で「平均律の場合、完全五度はそれぞれ純正音程よりもピタゴラスコンマの1/12だけ狭められているため、」とあるのも、完全五度は7半音ですから、「平均律の完全五度は純正音程の完全五度（1：1.5）よりもピタゴラスコンマの7/12（7半音分）だけ狭められて、およそ 1：1.4983 となっているため、」というような説明にしないとわかりにくいのではないでしょうか。1.4983 というのはもちろん128の12乗根です。わたしが 2：3 でなく 1：1.5 という表現を使ったのも、ここでの説明が容易だからです。--Tamie（会話） 2019年5月5日 (日) 22:53 (UTC)

Tamieさんの平均律の理解は誤っています。平均律の完全五度は純正音程より1/12ピタゴラスコンマだけ狭められています。--Kagefumimaru（会話） 2019年5月5日 (日) 23:15 (UTC)

それから異名同音関係の利用は説明に不可欠です。たとえばお聞きしますが、Cから12回完全五度上昇した音は何ですか？--Kagefumimaru（会話） 2019年5月5日 (日) 23:30 (UTC)

平均律は半音あたりピタゴラスコンマの 1/12 だけ狭められて、オクターヴでちょうど 2倍になる（元に戻る）のではありませんか？　完全五度は7半音分ですから、7/12だけ狭いのではないでしょうか。Cから12回完全五度上昇した音は、Cよりピタゴラスコンマ（約1/4半音）だけ高い「ほぼC」の音でしょう。それを何と呼ぶか、わたしは音楽の専門教育を受けた者ではないのでそこまでは知りませんが、それは単に「名付け方」だけの問題であり、五度圏が閉じないことと直接の関係はないですよね。--Tamie（会話） 2019年5月6日 (月) 00:02 (UTC)

あなたの平均律の理解は完全に間違っています、とりあえず平均律をお読みください。Cから12回完全五度上昇した音はB♯です。CとB♯は全く異なる音です。--Kagefumimaru（会話） 2019年5月6日 (月) 00:07 (UTC)

失礼しました、完全五度については納得しましたので取り下げます。しかし「Cから12回完全五度上昇した音はB♯」とありますが、このB#が、Cよりピタゴラスコンマだけ高い音のことですから、間違っていませんよね。それを単にB#と呼ぶだけのことであり、平均律のB#と同じわけではありません。異名同音の説明が必要とお考えなら、五度圏の図の6時の位置にある音について、Cから6回上昇して得られる嬰ヘと、逆に6回下行してえられる変トの間にピタゴラスコンマだけの差が生ずると説明されるとわかりやすいのではありませんか。--Tamie（会話） 2019年5月6日 (月) 00:22 (UTC)

閉じた状態を説明せずに閉じないことを説明することなど出来ません。 G♭と F♯のあいだに差が存在するというだけでは何も説明していません、異名同音の慣習を前提としなければそれは当たり前です。それはG♭= F♯とみなすことで五度圏は閉じるという説明があってはじめて意味をなします。--Kagefumimaru（会話） 2019年5月6日 (月) 00:36 (UTC)

もしどうしても「12の純正な完全五度と7オクターヴとの差」について盛り込むのでしたら、脚注を利用してこのように説明すべきだと考えます。

「実際には純正な完全五度の連鎖から得られるピッチクラスは閉じた環を形成しない。閉じた環とするには G♭ / F♯ のような異名同音関係を利用する必要があるが、純正な完全五度を連鎖させた場合は異名同音のあいだに約23.46セントの差が生じる＜注＞。この差はピタゴラスコンマと呼ばれる。」

注：例えばG♭から12回の完全5度の上昇によってF♯に達するが(G♭-D♭-A♭-E♭-B♭-F-C-G-D-A-E-B-F♯)、これを純正な完全5度(3/2)で行った場合の音程(3/2)^12は、元のG♭の7オクターヴ上(2/1)^7のG♭に対して3^12/2^19＝531441/524288の差が発生し、これは約23.46セントである。

しかし私はこのような内容はピタゴラスコンマの記事で説明すべき内容だと考えますし、あまつさえ五度圏の記事にこのような説明抜きに「12の純正な完全五度と7オクターヴとの差」を突然持ち出すのは言語道断と考えます。--Kagefumimaru（会話） 2019年5月6日 (月) 03:53 (UTC)

「言語道断」というほど問題とは思いません。すみませんが、それはKagefumimaruさんの主観的嫌悪感のようにすら感じます。ピタゴラスコンマの内容は正しいですが、五度圏を読んで「ピタゴラスコンマって何だろう？」と思った人がクリックしても、中には「何だか難しいな。理解できなくていいや」となって戻ってしまう人が何割かいると思います。以下に私の案を示します。

「実際には純正な完全五度の連鎖から得られるピッチクラスは閉じた環を形成しない。閉じた環とするには G♭ / F♯ のような異名同音関係を利用する必要があるが、純正な完全五度を連鎖させた場合は異名同音のあいだに約23.46セントの音高差が生じる＜注＞。この差はピタゴラスコンマと呼ばれる。」

注：例えばG♭から12回の完全5度の上昇によってF♯に達するが(G♭-D♭-A♭-E♭-B♭-F-C-G-D-A-E-B-F♯)、これを純正な完全5度(2:3＝1:1.5)で行った場合 1.5¹²≒129.746337890625 となり、元のG♭の7オクターヴ上のG♭（2⁷＝128）との間に音高差が発生し、これが約23.46セントである。

差が生じる理由についてはKagefumimaruさんの説明も適切ですが、tamieさんの説明の方がより分かり易いのでtamieさんの説明方法を用いました。--Gruppetto（会話） 2019年5月6日 (月) 05:06 (UTC)

音程を小数で表記することは無意味な数字の羅列となって不適切ですし、演算の過程が全く見えませんし、この場合ピタゴラスコンマの正確な値も示されていません。小数表記のどこがわかりやすいと考えたのか説明してください。もし上述の分数や乗数の表記が見づらいと理由でしたら実際にはTeXで表記しますから問題ありません。そしてピタゴラスコンマの記事の内容が分かりづらいと考えるのなら、ピタゴラスコンマを修正すべきです。何故問題を五度圏に持ち込むのですか？--Kagefumimaru（会話） 2019年5月6日 (月) 05:20 (UTC)

Kagefumimaruさんの説明も適切なのは分かります。しかし、数学がそれほど得意でない人には、tamieさんの説明の方が分かり易いと思います。ピタゴラスコンマの分かりにくさについては、それはそれ、これはこれで、それぞれが分かりやすさを目指せば良いのです。--Gruppetto（会話） 2019年5月6日 (月) 05:35 (UTC)

だから小数表記のどこがわかりやすいのか具体的に説明してください--Kagefumimaru（会話） 2019年5月6日 (月) 05:40 (UTC)

少数表記だとなぜ分かりにくいのか説明して下さい。--Gruppetto（会話） 2019年5月6日 (月) 05:46 (UTC)

上述のとおりです、無意味な数字の羅列となること、演算の過程が全く見えないことです。また音楽理論の文献で音程が小数で表記されることはありません、それでは解りづらいからです。たとえばニューグローヴ音楽事典のピタゴラス音律の記事から例を引用します "The ratio for the octave is 2:1, and for the 5th 3:2. To find the ratio for the sum of two intervals their ratios are multiplied; to find the ratio for the intervallic difference, the ratios are divided. The ratio for the 4th is 4:3 (octave – 5th, hence 2:1 ÷ 3:2); for the whole tone, 9:8 (5th – 4th, hence 3:2 ÷ 4:3); for the major 6th, 27:16 (5th + whole tone, hence 3:2 × 9:8); for the minor 3rd, 32:27 (octave – major 6th, hence 2:1 ÷ 27:16, or 4th – whole tone, hence 4:3 ÷ 9:8); for the ‘ditone’ or major 3rd, 81:64 (whole tone + whole tone, hence 9:8 × 9:8); for the ‘limma’ or diatonic minor 2nd, 256:243 (4th – major 3rd, hence 4:3 ÷ 81:64); for the somewhat larger ‘apotomē’, 2187:2048 (whole tone – limma, hence 9:8 ÷ 256:243) and so on." もしこれが小数で表記したら理解が困難で不適切です。--Kagefumimaru（会話） 2019年5月6日 (月) 05:52 (UTC)

そうですか。私にはtamieさんの説明の方が分かり易いです。--Gruppetto（会話） 2019年5月6日 (月) 06:00 (UTC)

何故わかりやすいのかを説明してください。--Kagefumimaru（会話） 2019年5月6日 (月) 06:01 (UTC)

私にはtamieさんの説明の方が分かりやすく、しかしそれはKagefumimaruさんにはむしろ分かりづらい、という事実があるだけです。なので私としてはtamieさんの説明方法を支持するのみです。他の方の意見を待つことにしましょう。--Gruppetto（会話） 2019年5月6日 (月) 06:31 (UTC)

だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月6日 (月) 06:37 (UTC)

活発な議論ありがとうございます。しかし、練れば練るほど、やっぱりわかりにくくなっていくように思えてなりません。わたしにはわたしが書いた記述がいちばん直感的でわかりやすいのですが... わたしにはKagefumimaruさんの「閉じた状態を説明せずに閉じないことを説明することなど出来ません。 」というところからして理解不能です。わたしは、五度圏はそもそも閉じないから、平均律という閉じる方法が考えだされたと思っているからですが。--Tamie（会話） 2019年5月6日 (月) 09:12 (UTC)

五度圏というイメージが使用されるようになったのは平均律の考案より後のことです。現代的な意味での五度圏図の最初の例は Johann David Heinichen Der General-Bass in der Composition(1728)であり、より古くはJoan Carles Amat Guitarra española(1586) にも円形に24の調を配したものが出てきますが、いずれにせよ平均律の思想に基づくものです。--Kagefumimaru（会話） 2019年5月6日 (月) 09:34 (UTC)

上記の私の案を少し修正してみました。

「実際には純正な完全五度の連鎖から得られるピッチクラスは閉じた環を形成しない。閉じた環とするには G♭ / F♯ のような異名同音関係を利用する必要があるが、純正な完全五度を連鎖させた場合は異名同音のあいだに約23.46セントの差が生じる＜注＞。この差はピタゴラスコンマと呼ばれる。」

注：例えばG♭から12回の完全5度の上昇によってF♯が得られる(G♭-D♭-A♭-E♭-B♭-F-C-G-D-A-E-B-F♯)。これを純正な完全5度(3/2)で行った場合、このF♯と、元のG♭の7オクターヴ上のG♭との差は ${\frac {\left({\frac {3}{2}}\right)^{12}}{2^{7}}}={\frac {3^{12}}{2^{19}}}={\frac {531441}{524288}}$ となり、これは約23.46セントである。

Gruppettoさんは議論を拒否しましたし、tamieさんは元より他者に判断を委ねるということですから、特に反対意見が寄せられない場合はこの案で記事を編集したいと思います。--Kagefumimaru（会話） 2019年5月6日 (月) 23:00 (UTC)

別に議論を「拒否」などしていませんよ。勘違いしないで下さいね。--Gruppetto（会話） 2019年5月9日 (木) 05:17 (UTC)

平均律の方が早いということですが、それは「現代的な意味での五度圏」という概念が文献上に現れたときというにすぎません。純正五度系列から音階を作ることはピタゴラスの時代から考えられていたのですから、紀元前から実践的な意味での概念は存在したのです。上記のKagefumimaruさんの新案は、なぜ音列をG♭から始めなければならないのかが、百科事典を読みにくるような多くの人にとっては理解しがたく、ますますわかりにくくなっているだけです。なぜわかりにくい分数表記を好まれるのか、当方には理解できません。分数で苦しむ小学生はたくさんいるんですよ。わたしは「他者に判断を委ねる」などと言ったことはありません。他の方の意見も聞きたいと言っただけです。Kagefumimaruさんの新案でなくGruppettoさんが書いてくださった現在の版の方が良いと考えますから、現在の版を維持すべきです。現状では 2：1 ですから、Kagefumimaruさんは勝手な編集をすべきではないと考えます。--Tamie（会話） 2019年5月6日 (月) 23:23 (UTC)

G♭からはじめるのはもちろん「G♭ / F♯ のような異名同音関係を利用する必要がある」という文を受けてのことであり、これ以上わかり易い例があるとは思えません。分数表記は前述の理由により小数表記より優れています。そもそもウィキペディアが分数を理解できない読者にまで配慮することは不可能です。--Kagefumimaru（会話） 2019年5月6日 (月) 23:51 (UTC)

そんなことはありません。現にGruppettoさんも、わたしの記述の方がわかりやすいと言われてますし、百科事典というのはそもそも平易であるべきです。Kagefumimaruさんは妙に「異名同音」ということばにこだわっておられますが、厳密な意味で異名同音というのは平均律におけるG♭とF#のような関係だけであって、純正五度系列から生じるG♭とF#はピタゴラスコンマだけズレているのですから「異名異音」です。この表現も混乱を引き起こすだけですから、ここで用いるべきではありません。現状の版からも削除すべきと考えてます。--Tamie（会話） 2019年5月7日 (火) 00:02 (UTC)

何故私の案がわかりにくいのかを具体的に述べてください。五度圏の説明に異名同音の概念は必須です、根拠としてニューグローヴ音楽事典の五度圏の項目では"Such an arrangement is dependent on an Enharmonic relationship somewhere in the circle"とあります。Enharmonic の訳語が「異名同音」という不適切な形で定着してしまったのは仕方のないことです、訳語の統一性の観点からこれを場合によって「異名異音」とすることはできません。また「エンハーモニック音」等の表記は解りづらいだけでしょう。--Kagefumimaru（会話） 2019年5月7日 (火) 00:12 (UTC)

参考までにen:Enharmonicをお読みください、異名同音は平均律だけに適用されるものではありません。--Kagefumimaru（会話） 2019年5月7日 (火) 00:19 (UTC)

異名同音をご覧ください。私は日本人なので、英語を正確に認識できないことの方が圧倒的に多いですから、英語でゴマかそうとしないでください。『音律と音階の科学』（講談社）にも、「音律によってはC#とD♭、D#とE♭等は異名異音になる」と書かれています。ズレているのに異名同音だという説明自体が矛盾していてわかりにくいし、そもそも純正完全五度で描いた五度圏は原理的に閉じないのです。だから、Kagefumimaruさんの「閉じた状態を説明せずに閉じないことを説明することなど出来ません。 」というところからして話が逆だと言っているのです。閉じないものを閉じるためにいろいろな音律が考えられたわけですから、閉じることを先に考える必要などありません。--Tamie（会話） 2019年5月7日 (火) 10:56 (UTC)

では「目が見える」という概念に依らず「目が見えない」ということを説明してください。--Kagefumimaru（会話） 2019年5月7日 (火) 11:00 (UTC)

先日コメントした者です。現在のお三方での議論だと平行線のままで、結論を出すのは難しいのではないかと思います（Gruppettoさんも同様のお考えであって、議論拒否というわけではないと思います）。性急に結論を急がず、第三者からの意見が出るのを待ってはいかがでしょうか。私は門外漢過ぎて有意義な意見を言えませんが、①語順は現行版が一番分かりやすい、②異名同音に関してはリンク先を読めば何となく分かるのであって困ることはない、③数式の難しさは小数でも分数でもどっちもどっち（数式はピタゴラスコンマの方で詳述するのがベストと思うんですが、この記事にあって悪いとまでは思いません）、④前にも述べた通りピタゴラス音律の記述と見比べたときに同じことを言っていると分かる形になればいいなあ、という感想です。五度圏という単語を実際に検索するのは一定の音楽知識はある人でしょうから、ある程度音楽に詳しい第三者の方から意見が出れば一番なのではないかと思います。--Nano blocks（会話） 2019年5月7日 (火) 11:03 (UTC)

Nano blocksさん、ありがとうございます。わたしもそう思っています。Kagefumimaruさんが反論されるので答えていますが、ここは第三者のコメントを依頼する場であって、我々ふたりがいくらやりあっても無意味ですよね。ただ、Kagefumimaruさんも改善案を示されていますから、わたしも以下にわたしなりの改善案を示して、他の方からのコメントを待ちたいと思います。

五度圏（ごどけん、英語：circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである。ハ長調を基準にして見ると、主音が5度上がる毎に調号の＃がひとつ増え、反対に5度下がる毎に♭がひとつ増えるという関係になっている。

しかし、純正な完全五度の周波数比は 2:3（＝ 1：1.5 ）なので、これを12回繰り返すと 1.5¹²≒129.7463 となり、7オクターヴ上（2⁷＝128）との間にわずかな差がある。この差をピタゴラスコンマという。このため、12時の位置にあるハの音から右回りに6回上昇して得られる嬰ヘと、逆に左回りに6回下降して得られる変トの間にピタゴラスコンマだけの差が生ずる。つまり、完全五度だけを繰り返す方法では閉じた環にはならず、少なくともどこか1か所は 1:1.5 の比率を崩さないと閉じることができない。

どの位置でどのように調節するかによって、さまざまな音律が生み出されてきた。例えば平均律は、完全五度を純正音程（1:1.5）よりもわずかに小さい、およそ 1:1.4983 （128の12乗根）とすることによって五度圏が閉じるように調節した音律であり、6時の位置の嬰ヘと変トは完全に一致し、異名同音となる。

以上です。--Tamie（会話） 2019年5月7日 (火) 12:45 (UTC)

五度圏によって音律が生み出されたかのような記述は歴史的事実に反するのでやめてください。五度圏とは調をサークルにした「図」であってそれに内包される原理と混同してはいけません。--Kagefumimaru（会話） 2019年5月7日 (火) 13:04 (UTC)

Wikipediaは歴史的事実だけを説く場ではありません。他のどんな学問も、必ず歴史の順に解説するわけではありません。--

Tamie（会話） 2019年5月7日 (火) 21:48 (UTC)

ウィキペディアに書いてよいのは事実だけです、あなたの妄想を書いていい場所ではありません。--Kagefumimaru（会話） 2019年5月7日 (火) 21:55 (UTC)

どちらが妄想なのか第三者のコメントをもらうのがこの場であり、そうしろとおっしゃったのはKagefumimaruさんです。--Tamie（会話） 2019年5月7日 (火) 22:01 (UTC)

当方の私案中の脚注が、ここではじゃまなので削除しました。--Tamie（会話） 2019年5月7日 (火) 22:05 (UTC)

17・18世紀の音楽家が音律の記述に五度圏を用いることはありませんでした。Tamieさんの記述は当時の音楽家が五度圏を想定していたような誤解を与える文章です。もうひとつ、この説明は嬰ヘと変トのあいだにピタゴラスコンマの差が生ずる理由を全く示していません。--Kagefumimaru（会話） 2019年5月7日 (火) 22:08 (UTC)

では、以下のように修正します。強調部分が変更箇所です。

五度圏（ごどけん、英語：circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである。ハ長調を基準にして見ると、主音が5度上がる毎に調号の＃がひとつ増え、反対に5度下がる毎に♭がひとつ増えるという関係になっている。

しかし、純正な完全五度の周波数比は 2:3（＝ 1：1.5 ）なので、これを12回繰り返すと 1.5¹²≒129.7463 となり、7オクターヴ上（2⁷＝128）との間にわずかな差がある。この差をピタゴラスコンマという。このため、12時の位置にあるハの音から右回りに6回上昇して得られる嬰ヘと、逆に左回りに6回下降して得られる変トの間にピタゴラスコンマだけの差が生ずる。つまり、完全五度だけを繰り返す方法では閉じた環にはならず、少なくともどこか1か所は 1:1.5 の比率を崩さないと閉じることができない。

どの位置でどのように調節するかによって、さまざまな音律が成立し得る。例えば平均律は、完全五度を純正音程（1:1.5）よりもわずかに小さい、およそ 1:1.4983 （128の12乗根）とすることによって五度圏が閉じるように調節した音律であり、6時の位置の嬰ヘと変トは完全に一致し、異名同音となる。

以上が私の第二案です。嬰ヘと変トのあいだにピタゴラスコンマの差が生ずる理由は明確に説明しています。--Tamie（会話） 2019年5月7日 (火) 22:17 (UTC)

コメント依頼から来ました。大変申し上げにくいのですが、問題になっている部分は、そもそも「五度圏」の説明としてどの程度必要なものなんですか？　例えば英語版のこの記事は構造や歴史、使われ方などの節立てになっており、私としては、これらはピタゴラスコンマや異名同音よりよほど重要に思えますが。

また、ここまでの長い長いやりとりで、出典（信頼できる情報源）がまったく示されないのはなぜなんでしょうか。みなさん、なにを元に議論しておられるのでしょうか？　どう書くかの前に、この記事に何が必要で何に基づいて書くのかを考えていただければと思います。--みっち（会話） 2019年5月8日 (水) 12:43 (UTC)

「五度圏が閉じない」ということはそれほど重要でない余談と言うべき事柄です。というより五度圏が閉じない、というよりは「五度圏の五度は平均律の五度である」というのがこの箇所の説明の述べる論旨です、結局は余談ですが。出典として既に提示してある William Drabkin, “Circle of fifths,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001). の冒頭部分を例として引用し、訳出してみます。

Circle of fifths (Ger. Quintenzirkel).

The arrangement of the tonics of the 12 major or minor keys by ascending or descending perfect 5ths, thus making a closed circle:

C–G–D–A–E–B–F♯ ＝ G♭–D♭–A♭–E♭–B♭–F–C

Such an arrangement is dependent on an Enharmonic relationship somewhere in the circle; this is usually reckoned at F♯/G♭ for the major keys and at D♯/E♭ for the minor keys. Normally the system of Equal temperament is assumed for the circle of 5ths, with every note having an infinite number of enharmonic equivalents (B♯ ＝ C ＝ D♭♭), though it is possible to use a tuning system in which certain 5ths are greater than the 12th part of the circle (e.g. pure 5ths) and others are commensurately smaller, so that the octave is still a closed circle. But in Pythagorean intonation, the system based entirely on pure 5ths, the ‘circle’ is open, since this system does not admit enharmonic equivalents. In the arrangement C–G–D–A–E–B–F♯–C♯–G♯–D♯–A♯–E♯–B♯, if all the 5ths are pure, then B♯ will be slightly higher than C. For this reason the arrangement of 5ths in the Pythagorean system can be represented by a spiral or coil, but not by a closed circle.

五度圏

12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたもの:

C–G–D–A–E–B–F♯ ＝ G♭–D♭–A♭–E♭–B♭–F–C

このような配列は異名同音関係に依存している、これは通常、長調ではF♯/G♭、短調ではD♯/E♭とみなすものである。一般に五度圏は平均律を想定しており、各音は無限の数の異名同音を有している(B♯ ＝ C ＝ D♭♭)、だが五度圏は環の12区分を超えるような五度（例えば純正五度）や小さい五度によるが、オクターヴはなおも閉じた環をなしているという音律を使用することもできる。しかし純正五度のみに基づくピタゴラス音律では「環」は閉じない、なぜならこの方法では異名同音が一致することが許されないためである。C–G–D–A–E–B–F♯–C♯–G♯–D♯–A♯–E♯–B♯という配列で五度がすべて純正な場合B♯はCよりも少しだけ高くなる。このためピタゴラス音律の五度の配列は閉じた環ではなく螺旋やコイルとなる。

以上、参考まで。--Kagefumimaru（会話） 2019年5月8日 (水) 17:55 (UTC)

「五度圏は閉じないので、ピタゴラスのコンマにどう対処するかは、ピタゴラス音律にとどまらず、その後現れたほとんどの音律に共通する大問題となった。歴史的な紆余曲折はあったが、これを一挙に解決してしまったのが平均律である云々」といったことが、既に5月7日の当方の記述に紹介した 小方厚著 『音律と音階の科学』 講談社 2007年 ISBN987-4-06-257567-6 に（比較的）わかりやすく書かれています。実際、音律というと現在はピタゴラス音律、純正率、中全音律、平均律くらいしか話題になりませんが、昔は「古典調律」とよばれるようなもっといろいろな音律が考えられており、何とかして響きの良い音律にしようという努力がなされていたようです。実際、ピアノのようにその場で即座に調律を変えることができない楽器では、もしハ長調で純正率に調律してしまうと、ハ長調の曲は美しく響くが、他の調に転調した途端に聴くに耐えないひどいものになってしまいます。わたしは専門家ではないので、これ以上うまく説明できませんが、結局ピアノのような鍵盤楽器では、転調が自由にできる平均律が採用されることになった、ということのようです。五度圏が閉じないというのは、それくらい大きな問題だったと言えると思います。--Tamie（会話） 2019年5月8日 (水) 22:39 (UTC)

それは音律の問題であって五度圏の記事に書くことではありません。--Kagefumimaru（会話） 2019年5月8日 (水) 23:13 (UTC)

「五度圏」「音律」「音階」は、全て深く関連し合うものであって、それはあっち、これはこっちなどと切り離して考えることではありません。五度圏が閉じないから、音律の問題が出てくるのです。もし五度圏が原理的に閉じているものであったら、音律や音階の問題で多くの学者や音楽家がさんざん苦労する必要はなかったわけですから。--Tamie（会話） 2019年5月8日 (水) 23:27 (UTC)

Tamieさんが述べているような問題の焦点は「異名同音が一致しないこと」であって「五度圏が閉じないこと」ではありません。さまざまな音律が考案されたのは別に五度圏を描きたかったからではありません。--Kagefumimaru（会話） 2019年5月8日 (水) 23:32 (UTC)

「五度圏」がそもそも平均律を前提としているのはわかりましたが、閉じない理由は余談として書いてあっても問題ありません。書くのであればtamieさんが示したような少数での表記を支持します。--Gruppetto（会話） 2019年5月9日 (木) 05:17 (UTC)

だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月9日 (木) 06:28 (UTC)

分数表記も適切なのはわかりますが、少数表記の方が平易なのは事実です。--Gruppetto（会話） 2019年5月9日 (木) 06:44 (UTC)

だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月9日 (木) 06:58 (UTC)

それを説明する必要はありません。少数表記の方がわかりやすい、という人が存在する、という事実があるのみです。--Gruppetto（会話） 2019年5月9日 (木) 13:22 (UTC)

Gruppettoさんの「説明する必要はありません」という主張はWP:DRで推奨されていないものです。だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月9日 (木) 13:31 (UTC)

違います。私は議論を否定しているのではなく、少数表記の方がわかりやすい、という人間がいる、という事実を無視してはいけない、と言っています。現時点では音高差説明に関しては2対1で少数表記が支持されています。--Gruppetto（会話） 2019年5月9日 (木) 13:42 (UTC)

小数表記のどこがわかりやすいのか具体的に説明していけない理由は何もありません。だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月9日 (木) 13:48 (UTC)

蕎麦よりうどんが好きな人に、蕎麦の方がなぜ美味いと感じるかを説明するのは不可能です。だからそこを議論するのは不毛です。--Gruppetto（会話） 2019年5月9日 (木) 13:54 (UTC)

ではあなたは不毛と知って私に『少数表記だとなぜ分かりにくいのか説明して下さい』と質問したのですか？そうではないはずです。だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月9日 (木) 13:59 (UTC)

不毛さをわかってもらう為に、そう質問したのです。--Gruppetto（会話） 2019年5月9日 (木) 14:06 (UTC)

私は小数表記のわかりにくさについて不毛ではない有意な説明をしました。だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月9日 (木) 14:10 (UTC)

Kagefumimaruさんの説明を読んでも、私は相変わらず少数表記の方がわかりやすい、というのが事実ですね。--Gruppetto（会話） 2019年5月9日 (木) 14:22 (UTC)

だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月9日 (木) 14:24 (UTC)

ですから、それを説明するのは不可能であり、現在は少数表記の支持者が多数だという事実があります。--Gruppetto（会話） 2019年5月9日 (木) 14:30 (UTC)

私は現に説明しましたし、あなたがずっと「少数」と書き間違えていることにいい加減イライラしています。だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月9日 (木) 14:36 (UTC)

そうでした「小数」ですね。私は小数表記の方がわかりやすいので、小数表記を支持します。分数表記の方が良いという意見が増えたなら、それに従います。wikipediaは多くの人のとってわかりやすくあるべきだからです。--Gruppetto（会話） 2019年5月9日 (木) 14:46 (UTC)

だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月9日 (木) 14:51 (UTC)

だからそれは不毛です。分数表記の支持者が増えたらそれに従いますが。--Gruppetto（会話） 2019年5月9日 (木) 14:56 (UTC)

私は小数表記のわかりにくさについて不毛ではない有意な説明をしました。だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月9日 (木) 15:02 (UTC)

いいえ。私はKagefumimaruさんの説明を読んでも小数表記の方がわかりやすいことに変わりはありません。だから不毛なのです。そこでどうするか。Wikipediaは多くの人にとって分かりやすくあるべきですから、分数表記の支持者の方が多数になったらそれに従います。--Gruppetto（会話） 2019年5月9日 (木) 15:06 (UTC)

支持者の多さということであれば既に述べたとおり音程の分数表記は当該分野での信頼できる情報源における標準的な表記法であり小数表記の追随を許しません。だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月9日 (木) 15:13 (UTC)

私の言っている支持者の多さとは、このノートページの議論での話です。--Gruppetto（会話） 2019年5月9日 (木) 15:28 (UTC)

支持者をこのノートページに限定するのは理不尽です。そもそもウィキペディアは多数決主義をとっていません。だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月9日 (木) 15:32 (UTC)

（インデント戻す）ウィキペディアは多数決主義をとっていませんが、私個人が、その議論の内容によっては多数決に委ねるのは私の自由なのであります。私個人としては、小数表記を支持することを重ねて表明いたします。--Gruppetto（会話） 2019年5月9日 (木) 16:44 (UTC)

あなたには対話相手との合意形成の努力を放棄する自由はありません。だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月9日 (木) 20:41 (UTC)

あなたに他人の自由を制限する権限はありません。--Gruppetto（会話） 2019年5月10日 (金) 04:20 (UTC)

Wikipedia:合意形成には『合意に向けた議論は常に「理由」を示して「相手を説得する」努力が求められます』とあります。したがってGruppettoさんがウィキペディアの編集に関与するなら合意形成の努力を放棄する自由はありません。だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月10日 (金) 13:08 (UTC)

理由は小数表記の支持者が多いという現実があるから、と再三示しています。この事実を見ようとしないKagefumimaruさんこそが、合意形成の努力を放棄しています。--Gruppetto（会話） 2019年5月10日 (金) 13:34 (UTC)

私は一度も小数表記の支持者が多いという説明を受けていません。だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月10日 (金) 13:38 (UTC)

そうやって都合の悪い話はなかったことにする、という態度は「合意形成の努力」とは到底言えませんね。Kagefumimaruさんがやっているのは合意する努力ではなく、議論相手を転ばせる努力です。--Gruppetto（会話） 2019年5月10日 (金) 14:16 (UTC)

見ての通り議論の過程は全て保存されていますから話をなかったことには出来ません。だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月10日 (金) 14:42 (UTC)

その説明は合意形成には不要なのでお断りします。--Gruppetto（会話） 2019年5月10日 (金) 15:13 (UTC)

Wikipedia:合意形成には『合意に向けた議論は常に「理由」を示して「相手を説得する」努力が求められます』とあります。だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月10日 (金) 22:14 (UTC)

ですから既に「理由」は示しました。--Gruppetto（会話） 2019年5月11日 (土) 04:18 (UTC)

だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月11日 (土) 04:29 (UTC)

もしも神様がこの世をお創りになったときに 1.5¹²＝2⁷＝128 という式が厳密に成り立つように産んでくださったなら、ピタゴラスの時代にすばらしくよく協和する理想的な音律が完成していたのです。ところが神様は少々意地悪なところがあって、1.5¹²≠2⁷＝128 なる世界をお創りになりました。だから純正五度を基本に作られたピタゴラス音階では、どうしてもハモらない音程ができてしまうのです。これを何とかしよう、少しでも美しく響くようにしようという目的で考え出されてきたのが、古典調律を含むさまざまな音律なのです。そうして最終的にピアノのような楽器では平均律という解しかないということになりました。だからピアノの和音はよく聴くと決してハモっていません。和音といっても、周波数が正確に単純な整数の比にはなっていないからです。つまり多くの研究者や音楽家が苦労して生み出してきた音律は、全て「五度圏が閉じない」ことに由来するハモらない音程を何とかしようという研究の歴史なのです。だから「五度圏が閉じない」という事実は、実は音楽学の根本的な大問題なのです。--Tamie（会話） 2019年5月9日 (木) 12:44 (UTC)

三度音程が無視されています。--Kagefumimaru（会話） 2019年5月9日 (木) 13:18 (UTC)

すいませんがtamieさんの話も五度圏とズレてしまってきているようです。「最終的にピアノのような楽器では平均律という解しかないということになりました」とおっしゃっていますが、そうはなっていません。現在は古楽の演奏では古典調律が用いられることもあります。電子楽器ではツマミ一つで様々な古典調律が選択できるものもあります。--Gruppetto（会話） 2019年5月9日 (木) 13:29 (UTC)

お二人とも情報源を示していただき、ありがとうございます。Tamieさんにはすでにお示しいただいていたのを見落としていたようで失礼しました。さて、確認させていただくと、私の理解では、五度圏は、（厳密には）平均律を前提にした異名同音による（依存した）環（サークル）であり、他の音律では環が閉じない、ということでよろしいでしょうか。このため、とくに鍵盤楽器の場合には平均律以外での調律は困難であったということですよね。お示しいただいた出典の文脈からはそのように読み取りました。Tamieさんが書きたい趣旨も同様ということであれば、このような書き方がいいのではないでしょうか。書きぶりとして注意すべきなのは、環が閉じないから調整して閉じさせる、とすると五度圏というよりも調律主体の説明となってしまい、違和感があります。なお私としては、すでに述べたように、この項目にとっては音楽理論上の五度圏の構造・役割、成り立ちなどが本筋であり、それ抜きでいきなり調律の話が出てくるのはバランスを欠くと考えます。このようないびつな構成では「閉じないものをなんで環と呼ぶのか」、「五度圏は実は環ではない」というような混乱や誤解が広まる恐れもありますから、この点はご配慮ください。あと、差を分数か少数点かで争うのも不毛ですからどちらも書かないか、あるいは断固絶対ぜーっったいどうしてもなにがなんでも譲れないなら両方書いたらいいです。くだらない。そんなことで争うヒマがあったら、ぜひ主要な説明を補強してください。私からは以上です。--みっち（会話） 2019年5月9日 (木) 14:40 (UTC)

『とくに鍵盤楽器の場合には平均律以外での調律は困難であったということですよね』それは全くの誤解です！こんなところで説明することでもないので、とりあえず中全音律ヴェルクマイスター音律ヴァロッティ音律あたりをちらっと眺めてください、これらはすべて鍵盤用の調律法です。--Kagefumimaru（会話） 2019年5月9日 (木) 14:49 (UTC)

みっちさん、Gruppettoさん、何度もコメントありがとうございます。私も音楽の専門家ではないのでなかなかうまく説明できず申し訳ないのですが、「私の理解では、五度圏は、（厳密には）平均律を前提にした異名同音による（依存した）環（サークル）であり、他の音律では環が閉じない、ということでよろしいでしょうか。」という部分は正しくありません。ピタゴラスの時代には既に、完全五度（2：3）の音程を重ねていくと、今日の平均律の音階にかなり近い音律が得られることがわかっていましたが、困ったことに完全五度を12回続けていくと、ほんの少し環が閉じないこともわかったのです。そこでピタゴラスはやむを得ずDEGABの音はCから五度ずつ上に求め、Fだけは1オクターブ上のCから五度だけ低いFにすることによってピタゴラス音階を定めたのです。そのため、この音階では上にも書いたように、どうしても美しく響かない音程が出てきます。これは根源的には「2と3は素数である」ということに由来するのですが、百科事典の記事でそこまで踏み込んで書くことはなかなか困難です。1冊の本になってしまうからです。何はともあれ、その美しく響かない音程を、何とかして少しでも美しく響くようにしたいということで、さまざまな音律が考えられ、ごく大雑把に言うとピタゴラス音律→純正率→中全音律→平均律というように流れてきたといえます。つまり、正確な言い方ではないのですが、五度圏というのは音律を考えるためのツールだともいうことができます。閉じない五度圏に由来するハモらない音を何とかしようとする結果、出てきた回答のひとつが平均律であり、これがピアノの普及とともに、最も一般的に受け入れられてきたということです。もちろん鍵盤楽器の音律も、いきなり平均律という解が出てきたというわけではなく、Kagefumimaruさんが言われるようなヴェルクマイスター音律などさまざまな試行錯誤があって、結局現在は平均律が最も一般的になったということです。--Tamie（会話） 2019年5月9日 (木) 22:54 (UTC)

書き漏らしましたが、「五度圏」が閉じないのは「完全五度だけを重ねていったとき」のことであり、ピタゴラス音階も純正率も中全音律も平均律も、比率をどこかで 2：3 から少しズラすことによって五度圏を閉じているのです。どの位置をどれだけ 2：3 からズラすかによって、さまざまな音律が生まれるということです。--Tamie（会話） 2019年5月9日 (木) 23:22 (UTC)

先ほど「五度圏が閉じない」のは、”根源的には「2と3は素数である」ということに由来する” と急にわけのわからないことを書いてしまいました。1.5¹²≠2⁷ という式は次のように変形することができます。(3/2)¹²≠2⁷ → 3¹²/2¹²≠2⁷ → 3¹²≠2⁷×2¹² → 3¹²≠2¹⁹。整数論によると、3^m＝2ⁿ を満たす m と n のペアは存在しないので、純正完全五度の環は、何周先まで伸ばし続けても決して閉じないということになるわけです。--Tamie（会話） 2019年5月10日 (金) 00:14 (UTC)

レスポンスいただいたので、もう1回だけ。Tamieさん、平均律のほかに（純正に限らず）完全5度を単純に重ねて環が閉じる音律はありますか？　なければ私の理解で正しいことになります。補足すれば、純正な完全5度の積み重ねでは閉じない環を、どのようにして閉じるかというのが、各種音律の派生理由ということですよね。Kagefumimaruさんには、後段の「とくに鍵盤楽器の場合には平均律以外による調律は困難があった」は、端折りすぎて意味が変わっていました。「平均律以外の調律では、（音律によって違いはあるものの）転調に困難があった」に修正します。

で、問題なのは、そうしてまで環を閉じたい理由はなにかということです。現状の記事ではこれが不明のままです。なぜ「環」なのかは、この記事の存在意義といってもいい。これは調整差をどう表すかなどよりもよほど重要ではありませんか？　これ以上は繰り返しませんが、この記事に何を書くのか、何を根拠とするのかを再度検討していただきたいと思います。コメント依頼の直接のお答えになっていないかもしれませんが、記事そのものの改善の方が私にとっても多くの利用者にとっても優先的ですし、改善によって些末な問題も解決に向かうでしょうから、そこはご了承ください。--みっち（会話） 2019年5月10日 (金) 10:10 (UTC)

みっちさん、こんにちは。もう一度まとめますと、(1)純正完全五度だけからなる五度圏は閉じない。ピタドラスコンマだけズレる。(2)しかし、例えばドから始めてレミファソラシドとあがっていったとき、最後のドは最初のドのちょうど1オクターヴ上でなくては困るわけです。音楽は何オクターヴもの音域があるのが普通ですから、実用の音律では必ずドとその上のドはちょうど1オクターヴでなければならず、ピタゴラスコンマだけズレていては困るのです。(3)そこで実用の音律では、五度圏のどこか少なくとも1か所は純正完全五度（2：3）から故意にズラして、五度圏をちょうど1周で閉じさせてやらなくてはなりません。(4)従って、実際に音楽に使われる音律はピタゴラス音律も純正律も中全音律も平均律も、全て五度圏が閉じるように調節されているわけです。ただ、その調節の仕方が音律によってそれぞれ違っているということなのです。(5)例えばピタゴラスは上にも書きましたが、C（ハ長調のド）から始めてDEGABの音はCから純正五度ずつ上の方にできる音を用い、Fだけは始めのCの1オクターブ上のCから五度だけ低いFにすることによって五度圏をとじるという方法でピタゴラス音階を定めたのです。(6)純正律においてはさらに長3度の和音が美しく響くように、5倍音をうまく取り入れて五度圏を閉じるのですが、ここまでくると、このノートページで説明するのは当方には荷が重いので、先に挙げた本をお読みいただけると幸いです。(7)平均律の場合は全ての五度を純正完全五度（2:3＝1：1.5）より狭くして約1：1.4983 とすることによって五度圏を閉じます。このため、平均律は全ての半音の周波数比率が同一（2の12乗根≒1.05946）になるので、転調しても違和感が全くなくなりますが、その代償として、どんな和音も純正には響かなくなるのです。でも、それほど音が濁るというほどではないので、現在の鍵盤楽器には最も一般的に採用されているわけです。(8)Kagefumimaruさんがおっしゃるように、音律は他にもいろいろなものが考えられていますが、結局どれも一長一短としか言えません。これ以上の詳しいことはここで述べるのは難しいです。(9)この記事に何を書くのかという点ですが、ここは「五度圏」の記事ですから、純正完全五度だけで音階を作るろうとすると、ピタゴラスコンマと呼ばれる差が生じて閉じないこと、実際の音階を作るためには、少なくともどこか1か所は純正完全五度を崩すしかないこと、その最もわかりやすい例として、単純に比率を全て均等に小さくする平均律がある、ということが書かれていればよいと考えます。それ以外の音律については、それぞれの音律に関する記事があるわけですから、それらを見ていただこうということです。音律と音階というのは実に奥が深く、昔から何人もの有名な学者が頭を悩ましてきた問題ですから、百科事典を読むだけで理解するのは到底困難ですから、こうした記事で「五度圏」って何となく面白そうだと思ったなら、やはりそれなりの書物をひもといてもらわないと無理です。百科事典というのは、そういうとっかかりになれば十分だと当方は考えています。--Tamie（会話） 2019年5月10日 (金) 11:53 (UTC)

同じことを再度申し上げますが、Tamieさんは問題の所在を完全に取り違えており、「異名同音が一致しないこと」と「五度圏が閉じないこと」を混同しています。例えるなら「液晶ディスプレイ」の項目で「パーソナルコンピューター」の動作を説明しようとしているようなものです。--Kagefumimaru（会話） 2019年5月10日 (金) 13:03 (UTC)

何で環なのかといえばいえば、任意の調からの転調の説明のためです。五度圏は本来的に和声的空間を視覚化する図であって、音律を考えるために作られたものではありません。--Kagefumimaru（会話） 2019年5月10日 (金) 13:26 (UTC)

The New Grove Dictionary of Music and Musiciansに「一般に五度圏は平均律を想定しており」とあるなら、このページもそのように説明した方が良いですね。現状は最後に平均律が出てくるので、環を閉じる為に様々な音律が生まれた、という誤解を生みやすいです。--Gruppetto（会話） 2019年5月10日 (金) 14:41 (UTC)

5月8日に書いた通り、小方厚著 『音律と音階の科学』 講談社 2007年 ISBN987-4-06-257567-6 には「五度圏は閉じないので、ピタゴラスのコンマにどう対処するかは、ピタゴラス音律にとどまらず、その後現れたほとんどの音律に共通する大問題となった。歴史的な紆余曲折はあったが、これを一挙に解決してしまったのが平均律である云々」と書かれているのですから「環を閉じる為に様々な音律が生まれた」というのは間違っておりません。ただ、それだけのためでなく、例えば完全五度以外に長3度の和音も可能な限り美しく響かせたい、できる限り転調がうまくいくようにしたい、といったさまざまな要求を満たすために実に多くの音律が考案されるに至ったわけですが、どの音律であろうと、全体として五度圏は必ず閉じていなければ、オクターヴ（1：2）という最も基本となる前提を満たしていないことになってしまうのです。--Tamie（会話） 2019年5月10日 (金) 22:43 (UTC)

「何で環なのかといえばいえば、任意の調からの転調の説明のためです。」とのことですが、「何のために作られたのか」ということと「何を表しているのか」ということは、本質的には関係のないことです。--Tamie（会話） 2019年5月10日 (金) 23:03 (UTC)

小方厚という方ですが、経歴を見ると専門は「ビーム物理」で、音楽家としてはアマチュアのジャズ愛好家、という点が気になります。音楽理論の歴史という面では必ずしも専門家とは言えないのではないでしょうか？--Gruppetto（会話） 2019年5月11日 (土) 04:36 (UTC)

日本大百科全書（ニッポニカ）では、確かに「平均律は、この螺旋を閉じた圏に収めようとする努力から考案されたとも解釈できる」とありますね。世界大百科事典では、「5度圏理論は西洋ばかりでなく，中国や日本にも古くから存在し，17世紀の朱載堉，および中根元圭の十二平均律理論の以前から実践的には5度圏によるエンハーモニックの解釈が行われていたと考えられる」とありますね。これはどう考えるべきか。--Gruppetto（会話） 2019年5月11日 (土) 12:23 (UTC)

Gruppettoさん、こんにちは。小方厚さんに関してはおっしゃる通りです。音楽家とか、そういう意味の専門家ではありませんが、物理学者だけあって理論的にはかなり踏み込んで、53音平均律や不協和曲線など、当方の手許にある専門書にも解説されていない内容までていねいに解説されています。音楽の専門家ではない人が書いたものを無暗に信用すべきでないと言われてしまうと、それ以上は何も言えませんが。
同じく平凡社の『音楽大事典』にも『世界大百科事典』と全く同じ解説があり、さらに「平均律以前の精密な音律論においては、5度螺旋が追及された」とあります。ピタゴラスの時代から5度音程による音階が研究され、ピタゴラスコンマが存在することまでわかっていたのですから、平均律よりずっと前の時代から五度圏という概念が存在し、あちこちで研究されていたということを言っているのではないでしょうか。エンハーモニックについてはたいへん長い記事になっていていろいろな定義が列挙されており、「全音・半音といったレベルからすれば同一階梯というに近い微小差」「音名と記譜法は異なるが、12平均律においては同音となるような関係をいうようにもなった」などなどとあり、Kagefumimaruさんの言われるようなF#とG♭におけるような小さな差を指すこともあるように見えます。残念ながらこのあたりのレベルになると、当方にはなかなか正確には理解しかねるところがあります。
ところでまことに恐縮なのですが、明朝から20日ほど現場に缶詰になる仕事が入ってしまい、非常時以外は外部との連絡が取れなくなってしまいました。期初の予定では当方の担当でなかったのですが、ピンチヒッターを命じられてしまいました。Gruppettoさんが分数よりはわかりやすいと言ってくださったことでもありますので、今回は5月7日にGruppettoさんが修正してくださった現在の版を以て、とりあえずこのコメント依頼は終了ということにさせてください。何卒ご了承をお願いします。活発な議論ありがとうございました。--Tamie（会話） 2019年5月11日 (土) 13:24 (UTC)

何の解決もしていないのに一方的に議論を放棄しないでください。議論を放棄するのであればあなたの編集以前に記事を回復することに同意してください。--Kagefumimaru（会話） 2019年5月11日 (土) 20:41 (UTC)

まことに申し訳ありません。「今回は5月7日にGruppettoさんが修正してくださった現在の版を以て」と書いたのは、当方が勝手に手出しをせずにという意味です。今回は当方の一方的な都合によるものなので、Kagefumimaruさんのご判断にお任せしますが、Gruppettoさんからいただいたご意見にも配慮していただけるならまことに幸いです。--Tamie（会話） 2019年5月11日 (土) 22:12 (UTC)

＞「議論を放棄するのであればあなたの編集以前に記事を回復することに同意してください」というの少々は勝手な言い分かと思います。--Gruppetto（会話） 2019年5月11日 (土) 22:16 (UTC)

当方はもう口出しすべきではないかもしれませんが、Nano blocksさんやみっちさんからいただいたご意見もあるわけですから、そのあたりも無視はせず、反映していただきたいと願っております。すみません、出発時刻です。--Tamie（会話） 2019年5月11日 (土) 22:31 (UTC)

Tamieさんは私に判断を任せると仰られ、Gruppettoさんは相変わらず小数点表記の利点について回答拒否を続けていますので、1週間ほど待って特に異論がでなければ 2019年5月5日 (日)の私の編集した版に戻します。--Kagefumimaru（会話） 2019年5月11日 (土) 23:18 (UTC)

それは勝手すぎますね。Kagefumimaruさんの案は誰の合意も得ていません。--Gruppetto（会話） 2019年5月12日 (日) 05:55 (UTC)

では小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月12日 (日) 07:07 (UTC)

急なことであせっておられたのでしょうし、事情はいたしかたないとは言え、一方的に自分の意見寄りの結論で議論を打ち切るTamieさんもよくないと思いますが、だからと言ってそもそもの議論前の状態に戻そうとするKagefumimaruさんもよくありません。事典類の表記と合わせて分数がよいというご意見自体はごもっともなので、私もどちらかといえば分数表記に賛成ですが、執拗に説明を要求する行為は明らかに議論を停滞させています（このノートを「具体的に説明してください」で検索するとすごいことになっています）。数学的には3/2だろうと1.5だろうと同じですし、その先の分かりやすさについて「感覚的なもの」以上の返答はできないでしょう。結論を急ぐ話でもないのですから、Tamieさんのお戻りを待って、あらためて落ち着いて議論をしていただけないでしょうか。

それはさておき、図書館で音楽事典をいくつか確認してきました。講談社『ニューグローヴ世界音楽大事典』に、五度圏が最初に記述されたのは1728年だとあったので、五度圏の図ができたの自体は平均律よりも後のことのようです。一方で、平凡社『音楽大事典』には「12平均律理論の以前から、実践的には5度圏によるエンハーモニックの解釈が行われていたと考えられる」とあり、この事典にのみ、五度圏以前の「五度螺旋」なるものについての記載もありました（一部Tamieさんがご提示済みですが、事典の記載はあくまで「考えられる」でした）。事典ごとに内容も説明の細かさもばらついていたので、どうも執筆者によって多少見解が割れるようです。TamieさんもKagefumimaruさんも、複数の出典を確認し、必要であれば複数の見解を併記する形をとるのがよいのではないかと思います。（あと、この記事とは関係ないのですが、確認した4つの事典はすべて「ピタゴラスコンマ」ではなく「ピュタゴラスのコンマ」でしたし、五度圏を「環」と表現している事典もありませんでした。Wikipediaの記事名が事典と表記が異なるのは英語の事典から直接訳したせいでしょうか？　これらの単語に関しては見ればわかるのでいいっちゃいいんですが、英語の事典を訳出するときは日本語版の事典の表記も確認した方がいいかと思います。）--Nano blocks（会話） 2019年5月12日 (日) 11:39 (UTC)

ウィキペディア日本語版ではピタゴラス表記が用いられているので「ピュタゴラス」表記は不適切ですし、調律関係の文献では普通「ピタゴラスコンマ」が用いられています[1]。--Kagefumimaru（会話） 2019年5月12日 (日) 12:12 (UTC)

そうなんですね！　承知しました。--Nano blocks（会話） 2019年5月12日 (日) 14:30 (UTC)

それから分数表記のわかりやすさについては感覚的なものではなく具体的に説明が可能です。たとえば小数表記ではわからない音程の複雑度が分数表記ではわかります、限界 (音楽)を参照してください。ピタゴラスコンマが3限界純正音程であることなど小数表記からは全くわかりません。そもそも小数表記ではそれが有理数なのか無理数なのかも判然としません。また小数表記は途中で略す必要がある事が多いため、正確さに妥協が必要ですが、分数表記はコンパクトに正確な値を示すことが出来ます。--Kagefumimaru（会話） 2019年5月12日 (日) 12:36 (UTC)

今得心しました。てっきり小数って1.5のことを指していると思いこんでいました、大変失礼しました。Kagefumimaruさんのご意見としては、①細かい数式はピタゴラスコンマの記事で書けばよく、五度圏の記事には不要②それでもこの記事に数式を載せるのであれば、正確な数値53441/524288を提示できる数式を用いるべき、という理解で合っていますでしょうか？　たいへん理にかなったご意見だと思います。けれども、文系の私は分数の上に分数がのっているだけで正直ウッとなるため、多少アバウトであっても小数表記が平易でよいとするTamieさんGruppettoさんのご意見もわかります（ただ、その場合そもそも五度圏の記事に数式は必要ないのではないかという最初の論点に戻る気はしますが、とりあえず置いておきます）。また、初めに「無意味な数字の羅列となって不適切ですし、演算の過程が全く見えませんし、この場合ピタゴラスコンマの正確な値も示されていません」と頭ごなしに否定するのでなく、今ご提示いただいたような書き方で穏当に説明していただければ、ここまで議論がこじれることはなかったのではないかと思います（これは発端のTamieさんの編集のリバートでも同じです）。私の今の個人的な感想としては、ピタゴラスコンマの方にKagefumimaruさんご提示の正確な数式があればこっちには数式はなくてもいいかなという気持ちになってきているのですが、前に述べた通りあって困ることもないとも思いますので、Tamieさんがお戻りになったら落ち着いて話し合い、双方の納得いく形にまとめてくださることを願います。--Nano blocks（会話） 2019年5月12日 (日) 14:30 (UTC)

同感です。私もtamieさんの戻るのを待ち、落ち着いて進めた方が良いと思います。--Gruppetto（会話） 2019年5月12日 (日) 14:36 (UTC)

私はGruppettoさんが編集した現在の版に不満です。だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月13日 (月) 06:04 (UTC)

では、議論のきっかけとなったtamieさんの最後の版に戻し、待つのも良いかもしれません。--Gruppetto（会話） 2019年5月13日 (月) 06:35 (UTC)

だから小数表記のどこがわかりやすいのか具体的に説明してください。--Kagefumimaru（会話） 2019年5月13日 (月) 06:39 (UTC)

小数表記とはまた別に、現状の記述は「12の純正な完全五度と7オクターヴとの差」という操作が脈絡なく導入されており説明になっていません。これに関して既にさんざん指摘しましたがGruppettoさんは回答を拒否し続けています。とりあえずピタゴラスコンマの方に説明を載せ読者の理解に配慮しましたが、現状のこちらの記事が意味不明であることは変わりありません。これに対する有効な釈明が示されない場合には当該記述を除去します。--Kagefumimaru（会話） 2019年5月15日 (水) 04:39 (UTC)

脈略がないとは思いません。勝手な編集はお控えください。--Gruppetto（会話） 2019年5月15日 (水) 06:01 (UTC)

現状の記述の「12の純正な完全五度と7オクターヴとの差」という操作がどのような脈絡で導入されているのか、それをどうやって読者が知るのかについて説明を求めます。--Kagefumimaru（会話） 2019年5月15日 (水) 06:09 (UTC)

人は柔軟な理解力を持ち、前後の文脈から理解します。--Gruppetto（会話） 2019年5月15日 (水) 13:25 (UTC)

説明を放棄したとみなして、当該記述を削除します。--Kagefumimaru（会話） 2019年5月15日 (水) 13:27 (UTC)

合意を得ない編集を強行するのはよろしくありません。--Gruppetto（会話） 2019年5月15日 (水) 13:31 (UTC)

「12の純正な完全五度と7オクターヴとの差」という操作がどのような脈絡で導入されているのか、それをどうやって読者が知るのかについて説明を求めます。--Kagefumimaru（会話） 2019年5月15日 (水) 13:40 (UTC)

お二人とも、実質的にスリー・リバート・ルールに抵触しているの、お気づきでしょうか。Tamieさんのお戻りを待つのであれば暫定的にどちらの版にしても同じです。とりあえず不毛な編集合戦はおやめください。--Nano blocks（会話） 2019年5月15日 (水) 14:07 (UTC)

当分の間編集を保留にするのであれば読者のために脈絡なく意味不明な記述を放置しておくべきではありません。Gruppettoさんはこれまでずっと回答の拒否や理由を述べない反対を続けて自分の行なった編集の版を強制しつづけています。これはWP:IDIDNTHEARTHATに該当すると考えます。--Kagefumimaru（会話） 2019年5月15日 (水) 14:30 (UTC)

誰の合意も得ていない編集を強行するKagefumimaruさんこそ、Wikipedia:妨害的編集#いつまでも納得しないに該当しています。「脈絡なく意味不明」はKagefumimaruさんの個人的感想に過ぎません。--Gruppetto（会話） 2019年5月15日 (水) 14:33 (UTC)追記--Gruppetto（会話） 2019年5月15日 (水) 14:36 (UTC)

では「12の純正な完全五度と7オクターヴとの差」という操作がどのような脈絡で導入されているのか、それをどうやって読者が知るのかについて説明を求めます。--Kagefumimaru（会話） 2019年5月15日 (水) 14:37 (UTC)

普通に読んだら文脈から理解できますね。--Gruppetto（会話） 2019年5月15日 (水) 14:40 (UTC)

「12の純正な完全五度と7オクターヴとの差」という操作がどのような脈絡で導入されているのか、それをどうやって読者が知るのかについて説明を求めます。--Kagefumimaru（会話） 2019年5月15日 (水) 14:50 (UTC)

「12の純正な完全五度と7オクターヴとの差」という言葉を目にした読者は考えを巡らせ、円形の図を見ながら「なるほど」と納得するでしょう。--Gruppetto（会話） 2019年5月15日 (水) 14:59 (UTC)

Wikipedia:アクセシビリティの観点から画像なしでは理解出来ない記事は推奨されません。また画像を見たところで12回の五度の連鎖で異名同音に到達することは自明ではありません。--Kagefumimaru（会話） 2019年5月15日 (水) 15:09 (UTC)

画像がなくても理解する人はいるでしょう。理解できなくともヒントになる。説明がないよりはマシです。--Gruppetto（会話） 2019年5月15日 (水) 15:17 (UTC)

先のあなたの説明において画像なしでどのように理解するのか、理解できない場合のヒントとは何のヒントなのか、支離滅裂な説明があることにより何がましになるのか具体的に説明してください--Kagefumimaru（会話） 2019年5月15日 (水) 15:25 (UTC)

やはりいつまでも納得しないのはKagefumimaruさんですね。通常の読解力があれば冒頭の「完全五度上昇あるいは下降する様に並べて閉じた環にしたものである」から瞬時に理解するのは明白です。--Gruppetto（会話） 2019年5月15日 (水) 15:29 (UTC)

自明であるのなら容易に具体的に理由を説明できるはずです。自明であるとして説明を放棄することは「[[[Wikipedia:論争の解決]]」及び「Wikipedia:合意形成」によって有効な意見表明と認められていません。--Kagefumimaru（会話） 2019年5月15日 (水) 15:34 (UTC)

（インデント戻す）冒頭に「五度圏（ごどけん、英語：circle of fifths）は、「12」の長調あるいは短調の主音を「完全五度」上昇あるいは下降する様に並べて閉じた環にしたものである」とありますね。新聞記事や試験問題を理解する読解力があったら普通はわかりますね。--Gruppetto（会話） 2019年5月15日 (水) 15:43 (UTC)

そこからどうやって12回の五度の連鎖で異名同音に到達することを知るのですか--Kagefumimaru（会話） 2019年5月15日 (水) 15:47 (UTC)

普通の読解力があればわかりますね。--Gruppetto（会話） 2019年5月15日 (水) 15:55 (UTC)

不可能です。可能であるというのならその過程を具体的に説明してください。--Kagefumimaru（会話） 2019年5月15日 (水) 15:57 (UTC)

あなたは上の方で「そもそもウィキペディアが分数を理解できない読者にまで配慮することは不可能です」と選民主義的なことを言いながら、ここでは突如文脈を理解できないフリをする。些か狡猾と言えるのではないでしょうか。--Gruppetto（会話） 2019年5月15日 (水) 16:07 (UTC)

話をそらさないでください、「12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである」という説明から読者が12回の五度の連鎖が異名同音に到達することを知る事ができる理由を具体的に説明してください。--Kagefumimaru（会話） 2019年5月15日 (水) 16:11 (UTC)

話を逸らしたのはあなたの方です。--Gruppetto（会話） 2019年5月15日 (水) 16:14 (UTC)

「12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである」という説明から読者が12回の五度の連鎖が異名同音に到達することを知る事ができる理由を具体的に説明してください。--Kagefumimaru（会話） 2019年5月15日 (水) 16:15 (UTC)

理解できないふりをしながら「具体的に説明して下さい」を繰り返す戦法には飽きました。--Gruppetto（会話） 2019年5月15日 (水) 16:18 (UTC)

「12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである」という説明から読者が12回の五度の連鎖が異名同音に到達することを知る事ができる理由を具体的に説明してください。--Kagefumimaru（会話） 2019年5月15日 (水) 16:21 (UTC)

通常の読解力の範囲内です。--Gruppetto（会話） 2019年5月15日 (水) 16:23 (UTC)

「12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである」という説明から読者が「12回の五度の連鎖が異名同音に到達する」ということを知る事ができる理由を具体的に説明してください。--Kagefumimaru（会話） 2019年5月15日 (水) 16:26 (UTC)

コメント Kagefumimaruさんは「具体的に説明してください」と29回も仰っているようですが、ただ説明を求めるだけでは議論は全く進みません。最低でも聞き方を変えるなどして、相手の考えを理解しようと努力していただけますでしょうか。--プログラム（会話） 2019年5月15日 (水) 16:28 (UTC)

論点を明確にしそれに集中すべきだと私は考えています。具体的にどのように聞き方を変えるべきでしょうか。--Kagefumimaru（会話） 2019年5月15日 (水) 16:32 (UTC)

もう一つ、プログラムさんは「12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである」という説明から読者が「12回の五度の連鎖が異名同音に到達する」ということを知る事ができる、と考えますか？--Kagefumimaru（会話） 2019年5月15日 (水) 16:42 (UTC)

論点ではなく「論法」に執着しているのではないでしょうか？--Gruppetto（会話） 2019年5月15日 (水) 16:39 (UTC)

報告 Gruppetto（会話 / 投稿記録 / 記録）さん、Kagefumimaru（会話 / 投稿記録 / 記録）さん共に3RR違反で3日間ブロックされました。--プログラム（会話） 2019年5月16日 (木) 14:00 (UTC)

コメント ピタゴラスコンマに関連する議論を続けるより、まず英語版から翻訳して記事を充実させるほうが良いと思いますが…--プログラム（会話） 2019年5月12日 (日) 15:38 (UTC)

とりあえずen:Circle of fifths 10:40, 11 May 2019 を‎ Historyの節まで訳してみました。しかしこれは質の低い記事で翻訳する価値があるとは思われません。

（以下翻訳）

英語版の翻訳

Circle of fifths showing major and minor keys

Nikolay Diletsky's circle of fifths in Idea grammatiki musikiyskoy (Moscow, 1679)

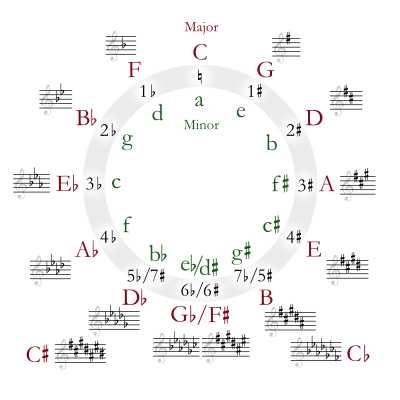
音楽理論において五度圏は、半音階の12の音と、それに対応する調号と、長調と短調の調の関係である。より専門的にいえば、ピッチクラス空間における半音階の12のピッチクラスを幾何学的に表現したものである。

定義

「五度」はオクターヴ以外ではもっとも協和する音程、あるいは数比であると定義できる。五度圏は次のピッチ（時計回り）が半音7つ分だけ高くなるように円形に配置されたピッチあるいは調の連なりである。音楽家や作曲家は五度圏をその中のいくつかのピッチの関係を理解しまた記述するために使用する。五度圏は作曲や和声づけ、コードの構築、楽曲における異なる調への転調などに有用である。

環の上方に位置するハ長調はシャープやフラットを持たない。上から時計回りに5度づつ進むと、Gメジャーはシャープが1つ、Dメジャーはシャープが2つ、等となる。同様に反時計回りに進むと、Fメジャーはフラット1つ、B♭メジャーはフラット2つ、等となる。環の下ではシャープとフラットの調が重なり、異名同音の調号の対が示される。

どの調から始めても平均律の五度づつ12の音を時計回りに巡ると最初のピッチクラスに帰還する。反時計回りに進む場合は完全五度ではなく完全四度進むことになる（四度の進行は落ち着いた、あるいは解決するという印象を与える。カデンツを参照）。

• 
   Play circle of fifths clockwise within one octave
• 
   Play circle of fifths counterclockwise within one octave

構造と使用

半音階に含まれるピッチは、半音という音程で隔てられているという関係だけでなく、五度圏において和声的に関係している。反時計回りの五度圏は「四度圏」となる。五度圏が典型的にはクラシック音楽の分析に使用されるのに対し、四度圏はジャズの分析に用いられる、とはいえこれは排他的ではない。五度圏はバーバーショップ音楽で要求される。Barbershop Harmony Society のコンテストの審査規定書によればバーバーショップ音楽は「他の解決も使用しながら、しばしば五度圏上で解決されるセブンス・コード」によって成立している。

全音階調号

五度圏は一般に全音階間の関係を示すのに使用される。五度圏上のアルファベットは長調の主音の音名を表している。五度圏内のシャープやフラットの数はその音階の調号が有するものである。すなわちA上の長調はその調号に3つのシャープを持ち、F上のそれは1つのフラットを持つ。

短調では、音名は反時計回りに3つずれる、すなわちAマイナーはシャープやフラットがなく、Eマイナーはシャープを1つ持つ（関係調を参照せよ）。この現象はこのように説明される、長調（たとえばGメジャーは1つのシャープ、すなわちF#をその全音階内に有する）の6度 (VI)から構築できる音階（関係短調、この場合はE）E-EにはG-Gと同じ音が含まれる。あるいはGメジャーの音階 (G–A–B–C–D–E–F#–G) とEマイナーの音階 (E–F#–G–A–B–C–D–E) はエンハーモニック（和声的等価）関係にある。

調号を書くとき楽譜にシャープを付す順序は、五度圏上のFからBへ、つまり F, C, G, D, A, E, B の順となる。たとえばGメジャーの調号の1つだけのシャープはFシャープであり、シャープが2つの場合FとCに付く、といった順序になる。このシャープの順番は五度圏上で時計回りになる（長調では最後のシャープは音階の7度音に付く、主音はその半音上になる）

フラットの場合はその逆で B, E, A, D, G, C, F の順になる。この順番は五度圏上で反時計回り、つまり4度進行である。FからCフラット (B) の五度圏上で反時計回りにある一連の調はこの順番で調号にフラットを付ける（長調では最後から2番目の調号のフラットは主音に付く、ただしフラットが1つしか無いFメジャーは例外）。

転調とコード進行

調性音楽はしばしば五度圏上で近隣の調に転調する。これはすなわち全音階は五度圏で隣接する7つのピッチクラスを含んでいるからである。また5度離れた調の音階に含まれる音の相違は半音1つ違うだけである。そのため完全5度による転調は非常にスムーズに行える。例えばCメジャー・スケール F–C–G–D–A–E–B から Gメジャー・スケール C–G–D–A–E–B–F♯ への転調で必要とされるのは "F" を "F♯" に変更することだけである。

五度圏によって近親調を簡単に見つけることができる。五度圏は各長調に対応する短調（エオリア旋法の）を示す。これはviのコード進行でもある。VとIVのコードは五度圏を時計回りあるいは反時計回りすることで見つけることができる。VとIVの対応短調はそれぞれiiiとiiである。

各長調のメジャー及びマイナー・コード

	I	ii	iii	IV	V	vi
C major	C	Dm	Em	F	G	Am
G major	G	Am	Bm	C	D	Em
D major	D	Em	F♯m	G	A	Bm
A major	A	Bm	C♯m	D	E	F♯m
E major	E	F♯m	G♯m	A	B	C♯m
B major	B	C♯m	D♯m	E	F♯	G♯m
F♯ major	F♯	G♯m	A♯m	B	C♯	D♯m
G♭ major	G♭	A♭m	B♭m	C♭	D♭	E♭m
D♭ major	D♭	E♭m	Fm	G♭	A♭	B♭m
A♭ major	A♭	B♭m	Cm	D♭	E♭	Fm
E♭ major	E♭	Fm	Gm	A♭	B♭	Cm
B♭ major	B♭	Cm	Dm	E♭	F	Gm
F major	F	Gm	Am	B♭	C	Dm

西洋の調性音楽ではそのルートが完全五度の関係にあるコード進行が見出される。すなわち D–G–C のようなルート進行が一般的である。このため五度圏はコード間の「和声的距離」を示すのに用いられる。

IV–V–I, in C  Play

ゴールドマンを含む理論家によれば和声機能（和声におけるコードの用法、役割、関係）は「五度圏によって説明される（これによりすなわちIIの音度はIVよりドミナントに近い）」。この観点からはトニックは五度圏がもたらすコード進行の向かう末端と考えられる。

ii–V–I progression, in C  Play subdominant, supertonic seventh, and supertonic chords illustrating the similarity between them.

ゴールドマンの Harmony in Western Music によれば「IVのコードは実際、最も単純な全音階関係のメカニズムではIから最も遠いところにある。（逆向きの）五度圏でいえばIに近づくよりもそれから遠ざかる」このため I–ii–V–I は I–IV–I よりも解決感が強い。ゴールドマンはナティエスの次のような主張に賛同している「4度のコードはIIのコードよりもずっと前に現れ、最後のIの次にある、I–IV–viio–iii–vi–ii–V–I" の進行でもトニックから遠い」。

IV vs. ii⁷ with root in parenthesis, in C  Play.

ゴールドマンはこのように言及している「IVのコードの和声設計における歴史的用法、特にカデンツにおけるそれには興味深いものがある。IVの終止形における用例は18世紀よりも19世紀において一般的となったもので、Vの前のiiの代替として理解されている。それは理論的には不完全なii7コード（ルートを欠く）でもある。」終止形におけるIV–Iの受容の遅れも五度圏の位置から説明できる。初期の IV–V–I の用法はiiを代替するIVとしてのIVとiiの関係を示している。しかしながらナティエスは後者の主張を引いて述べる「間一髪：ルート抜きのiiコードという理論だけがゴールドマンがバッハからワーグナーまで五度圏が完全に有効であるとすることを許す」。

非平均律における環の閉鎖

楽器が平均律で調律されている場合、5度の大きさは五度圏が「閉じる」ようになっている。これは12の5度をどのピッチから出発して上昇しても正確に最初のピッチクラスに帰還するということであり、正確にいえば7オクターヴ上の音に至る。このように五度圏が閉じているためには5度が純正音程（周波数比3:2）より若干狭く調整されていなければならない。

すなわち純正な5度による上昇では五度圏が閉じるよりも約23.46セント超過する、これは半音の約1/4であり、ピタゴラスコンマとして知られている音程である。この問題は12の5度のどれか1つを狭くすれば解決するが、そうするとその5度はひどく不協和になる。この変則的な5度は不快な音のユーモラスなメタファーとしてウルフの5度と呼ばれる（調子はずれの音を狼の吠え声に例えている）1/4コンマ中全音律では11の五度が平均律よりも狭く調整され、そのため五度圏を閉じるためにより大きくよりひどいウルフの5度が引き起こされる。5限界純正律のような純正音程によるより複雑な音律では最大8つの純正5度と最小3つの非純正5度（そのいくつかは純正よりも狭く、いくつかは広い）が五度圏を閉じるために用いられる。他の音律では五度圏を閉じるのに53もの音（元の12音に加えて42の音その間に配される）が使用される。

非専門的説明

Playing the circle of fifths
1 octave, fourths, descending 1 octave, fifths, ascending 2 octave, fifths, ascending 2 octave, fourths, descending 2 octave, fourths, ascending 2 octave, fifths, descending multi octave, fifths, ascending multi octave, fourths, descending multi octave, fourths, ascending

5度のような音程を見るのに簡単な方法はピアノの鍵盤を見ることであり、どの音から始めてもいいが、7つのキーを数えながら右に向かって弾けば（白鍵と黒鍵どちらも、最初のキーは勘定に入れない）五度圏の次の音になる。7つの半音、つまりピアノの最初と8つ目のキーの隔たりを「完全5度」と呼ぶ。「完全」とは長調でも短調でもないということであるが、そのどちらの音階にも現れる。そして「5度」というのは、鍵盤では7つの半音ではあるが、長調及び短調の音階で5つの隣り合う音を隔てた音のためである。

完全5度は純正音程の場合も調整された場合もある。3:2の比にある音程は純正な完全5度である。五度圏を1周して元のピッチクラスに帰るには3：2の比はわずかにずらされなければならない。音律を調整することで五度は循環するようになり移調が可能になる、つまりピアノや他のピッチが固定された楽器でどの調でも響きを破綻させずに演奏することができる。西洋の楽器（特にキーボードやフレット楽器）で第一に使用される音律は12平均律であり、半音を2^1/12とするものである。この場合、完全5度は2^7/12:1 (or about 1.498307077:1)となり、3:2の純正な完全5度よりも約2セント狭い。

歴史

1670年代後半に作曲家で理論家であるニコライ・ディレツキによって書かれた Grammatika は作曲に関する論文で、この種の著作としては最初に西洋式のポリフォニー作曲法を論じたものである。これはア・カペラ様式のポリフォニー音楽の作曲法を教えており、それは一般に典礼文に基づいて、リズム、拍子、旋律素材、合唱隊において対象的な楽章をまとめて作られるものである。ディレツキは彼の論文で作曲法だけでなく音楽理論も説明することを意図している。Grammatika は五度圏を作曲のための道具として示した最初の例である。

（とりあえずここまで）--Kagefumimaru（会話） 2019年5月13日 (月) 05:42 (UTC)

議論の続き

解決済み後続議論の#議論の仕切り直しにて合意形成済み--610CH-405（会話） 2019年7月14日 (日) 12:40 (UTC)

質が低いと考える理由は何でしょうか。誤った記述が含まれる可能性が高くなければ翻訳するほうが良いと思います。本題からは外れますが、Wikipedia:翻訳のガイドラインは帰属表示義務違反にならないためのものなので、ノートページにも適用されます。翻訳元がコメント中に書いてあったため帰属表示は行われていると判断し削除依頼には出しませんが、ノートページの本文は書き換えられる可能性があるため履歴継承は要約欄で行ってください。--プログラム（会話） 2019年5月13日 (月) 17:21 (UTC)

履歴継承の不手際については申し訳ありませんでした。質が低いと考える理由ですが、まず冒頭文からして何の説明にもなっていないことは読めばおわかりになると思います、誤ったことが書いてないから良いというものではありません。以降も冗長で支離滅裂な記述が続き、五度圏を理解する助けになるとは思えません、"In lay terms"節などまったく誤解のもとでしかないでしょう。この後の翻訳していない"Use"節も無駄に譜面を引用しながら五度圏とおよそ関係のない薀蓄を羅列するだけの酷いものです。結論として英語版の記事は構成内容共に多少の手直しでどうにかなるものでもなく、参考にすることすら勧められません。--Kagefumimaru（会話） 2019年5月14日 (火) 00:35 (UTC)

参考までに私による記事全体を書き換えた文案を提示します。典拠を明確にしたことが主な改善点です。

五度圏（ごどけん、英語：circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである(注1)。

五度圏は F♯/G♭ や D♯/E♭ といった異名同音関係を利用することで環を形成しており、これは一般に平均律を前提としている(注1)。純正な完全五度 (3/2) に基づくピタゴラス音律では異名同音は一致しないため閉じた環を形成できない(注1)。12の純正な完全五度の連鎖は元のピッチクラスに帰還せず、7オクターヴを約23.46セント超過し、この差はピタゴラスコンマと呼ばれる(注2)。平均律の完全五度は純正音程よりも1/12ピタゴラスコンマだけ狭められているため、異名同音が一致し、一様な五度によって閉じた五度圏を形成することができる(注3)。

五度圏はある調から他の調への「遠隔度」を説明するのに用いられる(注1)。例えばト長調に対し五度圏上で隣接する5つの調（ホ短調、ニ長調、ロ短調、ハ長調、イ短調）は和声的に近い関係にある近親調である（注4）。一方、五度圏上で最も離れた嬰ハ長調とは疎遠であり、その音階上の三和音に共通するものが1つもない（注5）。

注1：William Drabkin, “Circle of fifths,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001). 注2：Clive Greated, “Comma,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001). 注3：Mark Lindley, “Temperaments,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001). 注4：Ryan J. Thomson, A Folk Musicians Working Guide to Chords, Keys, Scales, and More, Captain Fiddle Publications, 1991. 注5：“Circle of fifths,” in The New Oxford Companion to Music, ed. by Denis Arnold, 1983.

--Kagefumimaru（会話） 2019年5月30日 (木) 10:58 (UTC)

Kagefumimaruさんは私の会話ページで「2018年4月27日(金)14:40の版に戻します」と執拗に繰り返しておられますが[2]、それは断固認められません。

しかし、↑上記の文案では「12の純正な完全五度の連鎖は元のピッチクラスに帰還せず、7オクターヴを約23.46セント超過し」とあるので、この通りにするなら反対しません。ただし、「7オクターヴを約23.46セント超過し」といった堅苦しい表現を「7オクターヴより約23.46セント高くなり」にするなどの細部の編集は行わせて頂く予定です。--Gruppetto（会話） 2019年5月30日 (木) 15:49 (UTC)

「約23.46セント高くなり」という記述が適当なのは五度の連鎖を高域に向かって行った場合だけであり、恣意的で不完全な表現であるので許容できません。--Kagefumimaru（会話） 2019年5月30日 (木) 16:07 (UTC)

2018年4月27日(金)14:40の版に戻すことが断固認められないというのであれば、Gruppettoさんは「12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである」という説明から読者が「12回の五度の連鎖が異名同音に到達する」ということを知る事ができる理由を具体的に説明してください。具体的な理由が説明されない場合WP:DR#2及びWP:CONACHIEVEに基づき五度圏の現在の記述が不適切であるということに関して有力な反論なしと判断し2018年4月27日(金)14:40の版に戻します。--Kagefumimaru（会話） 2019年5月30日 (木) 16:10 (UTC)

ほう。他人の意見を一切受け入れないという立場なんですな。ならばあなたのこの案への賛成は取り消す。純正な完全5度の連鎖では5度圏の環が閉じないことを一般の人にもより明確に簡潔に示したtamieさんの版を支持するのみですね。--Gruppetto（会話） 2019年5月30日 (木) 16:34 (UTC)追記--Gruppetto（会話） 2019年5月30日 (木) 16:51 (UTC)

典拠がニューグローヴに偏りすぎなのを改善し、あわせてピタゴラスコンマの解説を改善した案を示します。

五度圏（ごどけん、英語：circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである(注1)。

五度圏は F♯/G♭ や D♯/E♭ といった異名同音関係を利用することで環を形成しており、これは一般に平均律を前提としている(注1)。純正な完全五度に基づくピタゴラス音律では異名同音は一致しないため閉じた環を形成できない(注1)。例えばE♭を起点として完全五度を12回上方向に堆積すると異名同音関係にあるD♯が得られる (E♭-B♭-F-C-G-D-A-E-B-F♯-C♯-G♯-D♯)、しかし純正な完全五度(3/2)による場合、このD♯とE♭は正確なユニゾンやオクターヴ関係にならずピタゴラスコンマの差が生じる(注2)。平均律の完全五度は純正音程よりも1/12ピタゴラスコンマだけ狭められているため、異名同音が一致し、一様な五度によって閉じた五度圏を形成することができる(注3)。

五度圏はある調から他の調への「遠隔度」を説明するのに用いられる(注1)。例えばト長調に対し五度圏上で隣接する5つの調（ホ短調、ニ長調、ロ短調、ハ長調、イ短調）は和声的に近い関係にある近親調である（注4）。一方、五度圏上で最も離れた嬰ハ長調とは疎遠であり、その音階上の三和音に共通するものが1つもない（注5）。

注1：William Drabkin, “Circle of fifths,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001). 注2：Margo Schulter, Pythagorean Tuning and Medieval Polyphony, 1998. 注3：Mark Lindley, “Temperaments,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001). 注4：Ryan J. Thomson, A Folk Musicians Working Guide to Chords, Keys, Scales, and More, Captain Fiddle Publications, 1991. 注5：“Circle of fifths,” in The New Oxford Companion to Music, ed. by Denis Arnold, Oxford University Press, 1983.

--Kagefumimaru（会話） 2019年5月31日 (金) 00:01 (UTC)

出典も含めた建設的な提案をありがとうございます。私としては、第2段落と第3段落は入れ替え、環の説明を先に、環が閉じない話は最後がよいと思います。また、近親調・遠隔調の説明については、図示でもっとも上に位置しているハ長調を軸にしてはいかがでしょう。具体的には、当該段落の若干の言い回し変更を含めて次のようになります。--みっち（会話） 2019年5月31日 (金) 11:11 (UTC)

五度圏はある調から他の調への「遠隔度」を説明するのに用いられる。例えばハ長調に対し五度圏上で隣接するト長調、ヘ長調及びこれらの平行調であるイ短調、ホ短調、ニ短調は和声的に近い関係にある近親調である。一方、ハ長調の反対側に位置する嬰ヘ長調及びその異名同音調である変ト長調はもっとも遠く、音階上の三和音に共通するものが一つもない。

2段落と3段落を入れ替えるのは文脈に齟齬をきたすこともなく問題はないと思います。ト長調を基準として説明をしているのは単に典拠に従っただけですが、これを変更しても問題ないでしょう。ただみっちさんの提案する文案の「これらの平行調」の「これら」にハ長調が含まれているのは文法的におかしいと思います。また「もっとも遠く」という表現では意味がよくわからないと思います。--Kagefumimaru（会話） 2019年6月1日 (土) 04:51 (UTC)

「これら」にハ長調が含まれていてもおかしいとは思わないし、平行調について説明があった方がただ羅列するよりも関係性がわかりやすいでしょう。後段は「遠隔度」についていっているのだから、「遠い」か「隔たっている」が表現としては妥当かつ正確で、「離れた」や「疎遠」の方がむしろよくわからないと思います。それとも「遠隔度」が間違いですか？　ともかく、私はこの記事を触るつもりはないので、あとはお任せします。--みっち（会話） 2019年6月1日 (土) 13:30 (UTC)

遠隔調だから「もっとも遠く」は十分理解できますね。「もっとも遠く」という表現は「意味がよくわからない」で、「離れた」はOKというKagefumimaruさん独自の言語感覚を強硬に主張されても、他者との合意は難しいと思いますよ。--Gruppetto（会話） 2019年6月1日 (土) 13:55 (UTC)

ここで主語として機能しているのは「ト長調、ヘ長調」であって「ハ長調に対し五度圏上で隣接する」はその修飾になっています、したがって後続の「これら」の範囲にハ長調を含むことは出来ません。「もっとも遠く」だけではこれが前の「五度圏上で隣接する」に対し対蹠点が幾何学的に五度圏上で最も離れているという意味にも取れますので、「和声的に最も遠い関係にある」といった表現をする必要があります。また私の文案の「離れた」はみっちさんの文案の「反対側に位置する」に対応するもので、みっちさんの文案の「もっとも遠く」に対応するのは「疎遠である」です。「疎遠」を幾何学的な意味合いにとることは不可能でしょう。また「遠い関係にある」という言葉は「僅かながら関係がある」という肯定的な意味合いを持つように思われます。日本語の「関係」を打ち消す言葉はどちらかという「関係が乏しい」という表現ではないでしょうか。ちなみに「遠隔度」は"remoteness"を訳したものですが、「関係が乏しい」という意味の言葉にせめて「遠」を含めるために「疎遠」という語を採用しました。--Kagefumimaru（会話） 2019年6月1日 (土) 17:52 (UTC)

どちらが表現として適切かは個々人の主観の要素も多い。そもそもこの議論の発端はTamieさんの表記を認めるか否か？でしたが、Wikipediaは共同作業の場である以上、必ずしも間違いとは言えない他者の表現を「意味不明」などとして執拗に取り去ろうとするKagefumimaruさんの編集姿勢は如何なものでしょうか。--Gruppetto（会話） 2019年6月2日 (日) 13:58 (UTC)

コメント こんにちは、Kagefumimaruさん。Wikipedia:検証可能性を高めるためにも、出典に巻数と頁数を付けていただけますか？例えば、注1)ですと、

• William Drabkin, "Circle of fifths" in The New Grove Dictionary of Music and Musicians, 2nd ed., edited by Stanley Sadie, Vol. 5 Canto to Classic rock, 866-867. London: Macmillan Publishers Limited, 2001, ISBN 1-56159-239-0.

という感じになるかと思います。それでは。--Takabeg（会話） 2019年5月31日 (金) 12:21 (UTC)

• William Drabkin, “Circle of fifths,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 5, pp. 866-867.
• Margo Schulter, Pythagorean Tuning and Medieval Polyphony,(http://www.medieval.org/emfaq/harmony/pyth.html ), 1998.
• Mark Lindley, “Temperaments,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 25, pp. 248-269.
• Ryan J. Thomson, A Folk Musicians Working Guide to Chords, Keys, Scales, and More, Captain Fiddle Publications, 1991, p. 52.
• “Circle of fifths,” in The New Oxford Companion to Music, ed. by Denis Arnold, Oxford University Press, 1983, vol. 1, p. 399.

以上です。ただ事典類では巻数や頁数を表記しても記述にアクセスする助けにはあまりならないと思います。--Kagefumimaru（会話） 2019年6月1日 (土) 04:38 (UTC)

投票

解決済み後続議論の#議論の仕切り直しにて合意形成済み--610CH-405（会話） 2019年7月14日 (日) 12:40 (UTC)

議論が停滞しているため、Wikipedia:論争の解決に従いWikipedia:投票を実地することを提案します。投票内容は「『12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである』という文は『12回の五度の連鎖が異名同音に到達する』ということを説明しているか、否か」です。投票期間は7月1日から1ヶ月間を予定しています。--Kagefumimaru（会話） 2019年6月24日 (月) 23:17 (UTC)

現在の投票案です。異論がなければ投票内容に関して合意が得られたと考え、この内容で投票を実行します。

投票の主題	『12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである』という文は『12回の五度の連鎖が異名同音に到達する』ということの説明になっているか。
投票場所	ノート:五度圏#投票
投票に先立つ議論	ノート:五度圏
投票者の資格	投票開始時点で自動承認された登録利用者であること。ただし多重アカウントによる投票は禁止します。
投票期間	2019年7月1日 (月) 00:00 (UTC) から 2019年8月1日 (月) 00:00 (UTC) まで。
投票のルール	「はい」か「いいえ」の2択で回答してください。

--Kagefumimaru（会話） 2019年6月27日 (木) 04:16 (UTC)

議論の発端と本筋はそこじゃないと思いますよ。議論の本筋と関係ない投票に何の意味があるのでしょうかね。--Gruppetto（会話） 2019年6月27日 (木) 17:19 (UTC)

論点は「説明抜きに『12の純正な完全五度と7オクターヴとの差』という操作を提示することの是非」であり「『12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである』という文は『12回の五度の連鎖が異名同音に到達する』ということの説明になっているか」というのはその問題の焦点です。後者の是非が決まれば前者の是非も定まります。--Kagefumimaru（会話） 2019年6月27日 (木) 17:26 (UTC)

• 反対 「いいえ」 依頼者票。『12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである』という文には「異名同音」という概念に導くものは何も無く、『12回の五度の連鎖が異名同音に到達する』ということの説明にはなりえません。そして『12回の五度の連鎖が異名同音に到達する』及び『五度圏は異名同音を利用して環を形成している』ということが事前に説明されなければ『12の純正な完全五度と7オクターヴとの差』という操作は意味不明です。--Kagefumimaru（会話） 2019年7月1日 (月) 00:43 (UTC)

• コメント Template:意見募集中を見てきました。投票実施に賛同されている方がいないのに勝手に始めては駄目でしょう。プロジェクト:クラシック音楽にもPortal:クラシック音楽にも意見募集を行った形跡が無いのですが、どういうことでしょうか？--切干大根（会話） 2019年7月1日 (月) 01:20 (UTC)

反対意見が無いので投票を開始しました。またこの議論はクラシック音楽とは特に関係がありません。--Kagefumimaru（会話） 2019年7月1日 (月) 02:30 (UTC)

• コメント 投票の主題も音楽を専攻したことのない大多数の利用者からすれば意味不明です。投票は取り下げた上で、プロジェクトかポータルで音楽系統の利用者に呼びかけをすることをお勧めします。--切干大根（会話） 2019年7月1日 (月) 01:34 (UTC)

予備知識の無い読者に理解できる説明になっているか、というのが論点ですし、単に文脈の整合性を問うているだけなので回答に特に音楽知識は必要無いと考えるのですが。--Kagefumimaru（会話） 2019年7月1日 (月) 02:30 (UTC)

Portal:音楽でコメント依頼を告知しました。--Kagefumimaru（会話） 2019年7月1日 (月) 04:01 (UTC)

• コメント 一連の議論を拝見しました。色々と意見が出されている中で、振りだし地点での投票実施のように感じられ、この投票を設けた意味がわかりません。また、WP:DR#4には、「マナーを守り議論を尽くしても合意に至るのが難しい場合には」とあります。第三者視点から見て、マナーを守って議論が尽くされたようには見えません。また、WP:GVOTEにおける「議論の要約、各意見を簡潔に並べたもの、などの投票前に論点がわかるもの、が用意できているか?」についても合意が得られているようには思いません。投票を一旦取り下げてはいかがでしょうか？ --610CH-405（会話） 2019年7月1日 (月) 04:36 (UTC)

投票を取り下げる事に否はありませんが、マナーを守って議論が尽くされていない、というのは具体的にどのような点から判断したものなのでしょうか、改善すべき点を教えてください。それから折角顔を見せていただけたのでしたら投票せずとも記事の是非について何かコメントを戴けないでしょうか。--Kagefumimaru（会話） 2019年7月1日 (月) 04:57 (UTC)

返信 (Kagefumimaruさん宛) まぁ、当事者たちが3RR違反でブロックされている時点で論外なのですが、一番目立って気になるのは、「分数か小数か」です。これに関して第三者から「どちらも譲れないなら併記すれば良い」などと意見が寄せられているにも関わらず「分数か小数か」の議論が継続されていました。あとは自分が納得できなければどの版に戻すだの漢字が間違ってるからイライラしてるだの個人的感想や感情に起因するコメントをするとか。これでは合意が得られるわけがないんですよ。第三者から見ても論点がどこかわかりにくいし、第一、荒れているノートに積極的に飛び込みたい人自体少ないでしょう。このノートにコメントが書かれれば書かれるほど合意が難しくなっているように思います。（「投票」というのは「最善を尽くした上でも合意が得られない場合の最終手段」でしょうから、そもそも手順が間違っているということになります。）

私は、当事者たちが議論を客観視できればよいと考えています。そうすれば、自分の立場でも考えられるし相手の立場でも考えられる。永遠の課題だとは思いますが、

• 注意を受けたら反論しようとする前に第三者視点でどう映っているか考える
• 自分へのメリットより記事やWikipediaへのメリットを優先する
• 今している議論が何のためにあるのか、原点や本質にその都度立ち返る

などをやってみてはいかがでしょうか？ 私自身、Wikipedia歴が1年未満で、これまでも自分の行動で議論をこじらせてしまったり、後で自分の言動を見直して顔から火が出そうになったり、勉強の日々が続いています。もう少し経験のある方ならもっとよいアドバイスが出来るのかもしれませんが、私に今言えるのはこの範囲です。

さて、「折角顔を見せていただけたのでしたら投票せずとも記事の是非について何かコメントを戴けないでしょうか。」とのことですが、論点がごちゃつき過ぎていて何を言えば良いのかわからないし、この荒れている状況で議論に飛び込んで有意義な対応が出来る自信がありません。感情的な物言いを排除し、論点を明確にした上で議論を仕切り直していただけるのであれば、積極的に記事に関する意見を表明する用意はあります。私自身、（普段編集している道路や災害の分野よりも）音楽関係が専門ではあるので、専門知識を要する高度な議論にも対応できます。

長文失礼しました。解決に向け、前向きな対応を期待します。--610CH-405（会話） 2019年7月1日 (月) 05:57 (UTC)

論点は一貫して明確で「説明抜きに『12の純正な完全五度と7オクターヴとの差』という操作を提示することの是非」です。これにコメントを戴けますか。--Kagefumimaru（会話） 2019年7月1日 (月) 06:25 (UTC)

返信 (Kagefumimaruさん宛) 「これにコメントを戴けますか。」→いいえ。あなたが「一貫して明確だ」と思い込んでいるだけです。よって、私の先程のコメントの通り、それに関する意見は述べません（私が「こうすれば意見を述べます」とした用件を満たしていないため）。訳わからん事案には「訳わからん」としかコメントできません。ただ、「この投票に至った手続きは不当だろう」、これだけは言えます。--610CH-405（会話） 2019年7月1日 (月) 06:48 (UTC)

ではどのようであったら論点が明確化されたと言えますか。その状態とそれに至る方法を教えてください。--Kagefumimaru（会話） 2019年7月1日 (月) 07:01 (UTC)

返信 私のコメントするしないの根拠をここでこれ以上述べるのは不適切なので、利用者‐会話:Kagefumimaru#「ノート:五度圏」についてで説明します（書いている途中なので投稿するまで少々お待ち願います）。--610CH-405（会話） 2019年7月1日 (月) 07:17 (UTC)

• コメント Gruppettoさんのコメントは明らかに投票に反対するものだと思いますが。--切干大根（会話） 2019年7月1日 (月) 10:05 (UTC)

それは反対意見ではなく質問だと考えますし、回答によって納得していただけたものと思いますが。--Kagefumimaru（会話） 2019年7月1日 (月) 12:19 (UTC)

皆さんの意見に従いこの投票は中止し、投票の告知は撤去しました。引き続きコメントは募集中です。--Kagefumimaru（会話） 2019年7月1日 (月) 12:20 (UTC)

コメント 今更ほじくり返すことでは無いかもしれませんが、4日しか経っていないのに反論が無いから納得していただけたというのは無理があると思いますよ。それから、切干大根さんが「反対意見」と仰っていますが、私も投票への反対意見だろうと思っていました（「何の意味があるのでしょうかね（、いや、ないだろう）」という反語だと思っていました）。ご本人に聞かなければわかりませんが、いずれにせよ反対よりの最終意見から最低でも1週間は待つべきだったでしょうね。--610CH-405（会話） 2019年7月1日 (月) 12:31 (UTC)

議論の仕切り直し

解決済み2019年7月14日 (日) 10:45 (UTC) の案により合意--610CH-405（会話） 2019年7月14日 (日) 12:40 (UTC)

これまでの経緯をまとめます。2019年5月5日のTamieさんの編集[3]により『12の純正な完全五度と7オクターヴとの差』という操作が記事に挿入されましたが、これは文脈を混乱させるものとしてkagefumimaruこと私は反対しました。私は『12の純正な完全五度と7オクターヴとの差』という操作は、事前に『五度圏は異名同音を利用して環を形成している』及び『12回の五度の連鎖が異名同音に到達する』といった説明がない限り、その由来と結果の意味するところが読者には理解不能だと考えます。TamieさんとGruppettoさんは、そのような説明抜きに『12の純正な完全五度と7オクターヴとの差』という操作の意味は理解できると主張していますが、その具体的根拠については示されていません。

プログラムさんの提案により英語版の記事を翻訳したりもしましたが、これは議論の本筋とは関係ありません。

『12の純正な完全五度と7オクターヴとの差』という操作の意味と、それによって五度圏が閉じないということは説明抜きに理解できるか、ということについての皆さんの意見を求めます。--Kagefumimaru（会話） 2019年7月1日 (月) 12:14 (UTC)

コメント 出典がほとんど無いスタブ記事の内容に関して「理解できるか意見を求めます」と言われても困ります。多数の文献を調べて、ある程度記事のレベルを上げてからにしてくれませんか？--切干大根（会話） 2019年7月1日 (月) 13:06 (UTC)

出典がないことと「理解できるか」ということにどのような関係があるのでしょうか。--Kagefumimaru（会話） 2019年7月1日 (月) 13:23 (UTC)

もし出典のない文にはコメントできないという場合は2019年5月31日 (金) 00:01 (UTC)に私が提案した文案についてコメントをお願いします。これはすべての記述の典拠を明確にしています。--Kagefumimaru（会話） 2019年7月1日 (月) 13:31 (UTC)

コメント（インデント修正しました）自分のコメントを打っている途中ですが取り急ぎ。ちょっと待ってください、このままだとこれまでの議論の二の舞を踏むことになりますよ。まず、切干大根さんの発言にも一理ある。後で根拠付きで書きますが、記事を充実させるという作業も進行していくべき。現在の記事の内容ではこの議論の主題にコメントできないという人もいるという事実が存在する、ただそれだけのことです。--610CH-405（会話） 2019年7月1日 (月) 13:34 (UTC)

コメント （連投失礼）それに、議論の発端となった編集内容についてコメントを求めているのに、議論の途中で出てきた案に急に意見を求め始めるのもおかしい。結局何を問いたいのか、それは「『12の純正な完全五度と7オクターヴとの差』という操作の意味と、それによって五度圏が閉じないということは説明抜きに理解できるか」でしょう。論点をわざわざ混乱させないでください。--610CH-405（会話） 2019年7月1日 (月) 13:39 (UTC)

コメント 仕切り直しありがとうございます。私は今日になって初めて五度圏の記事や関連する議論を読みました。結論から率直に申し上げますが、Tamieさんによる編集の直後の 2019年5月5日 (日) 00:31 (UTC) の版 と、Kagefumimaruさんによるリバートの直後の 2019年5月5日 (日) 04:57 (UTC) の版 はどちらも説明として不十分であると考えます。もっと言えば、その後のすべての版について、説明が不十分。Kagefumimaruさんが意見を求めている点に焦点を当てて言い換えれば、「『12の純正な完全五度と7オクターヴとの差』という操作の意味について説明は不十分ではない」ということです。だからと言って、直後のリバートのように該当記述を消したところで五十歩百歩だ、これが私の言いたいことです。

そもそも切干大根さんの仰るように記事のレベルを上げるべきという話は付いて回ってきます。手っ取り早くは英語版からの翻訳でだいぶ記事は充実するように思いますし（英語版での出典も文献として辿ることが出来る）、そもそも「何に使うのか」「何のためにあるのか」という実態を書かないで「五度圏は閉じない」などの実用上あまり意識されていないことを書くのには違和感を感じます。ですので、記事を充実させる作業も進行して行くべきであることは頭に入れておいてください。

話を本題に戻します。私が「説明が不十分」と考える根拠を以下に述べます。まず、なぜ異名同音の考え方を使うのかが説明できていません。次に、なぜ12音なのかが説明されていません。すなわち、「純正な完全五度の周波数比は 1：1.5 なので、これを12回繰り返す」との記述に正当性を持たせることができません。さらに、「平均律の場合、完全五度はそれぞれ純正音程よりもピタゴラスコンマの1/12だけ狭められている」における1/12とは何なのかも説明できていません。

上記の例のほかにまだ出そうと思えば出てくるかもしれませんが、どっちにしろ突っ込みどころ満載なので、根本的に説明のロジックを一から見直して書き直すしかないでしょう。--610CH-405（会話） 2019年7月1日 (月) 13:57 (UTC)

「なぜ異名同音の考え方を使うのかが説明できていません」「なぜ12音なのかが説明されていません」ということが問題であるならばニューグローヴ音楽辞典の記述 （2019年5月8日 (水) 17:55 (UTC)参照）は不十分ということでしょうか。「純正な完全五度の周波数比は 1：1.5 なので、これを12回繰り返す」というのはTamieさんによる追加で私の意図するものではありません。「完全五度はそれぞれ純正音程よりもピタゴラスコンマの1/12だけ狭められている」というのは五度圏の完全五度は12個なのですから理解できると思います--Kagefumimaru（会話） 2019年7月1日 (月) 14:11 (UTC)。

もし「根本的に説明のロジックを一から見直して書き直すしかないでしょう」ということでしたら2019年5月31日 (金) 00:01 (UTC)の案を見てくださいということになるのですが、それだとちょっと待ってください、このままだとこれまでの議論の二の舞を踏むことになりますよということになりますから、『12の純正な完全五度と7オクターヴとの差』という操作の意味と、それによって五度圏が閉じないということを理解するのに必要なものは何か、ということに論点を絞っていただけないでしょうか。--Kagefumimaru（会話） 2019年7月1日 (月) 14:49 (UTC)

書き込もうとする度に編集が競合するので、あえて古い版のまま以下に書きます→私も『12の純正な完全五度と7オクターヴとの差』という内容は「異名同音を利用して環を閉じる」という説明があった後の方が良いと思いますよ。だからこそ私は2019年5月5日 (日) 23:40（日本時間）の編集で『12の純正な完全五度と7オクターヴとの差』という内容を「異名同音関係を利用する必要がある」の下に移しましたが、それすらもKagefumimaruさんはバッサリ差し戻しましたよね[4]？なのに何故今更これを「投票」まで考える程の論点だとKagefumimaruさんがお考えなのか、矛盾していて理解できません。そして重要な論点はそこではないと私は考えます。『12の純正な完全五度と7オクターヴとの差』という内容は「異名同音を利用して環を閉じる」という説明があった後の方がベターですが、逆になったからといって突然全く理解不能になるわけではないでしょう。はっきり言えばどちらでも良いくらいです。だからそこは論点の中心にはなりえません。

ノートページの冒頭を見れば、何が議論の発端だったのかは明確です。tamieさんの書いた「純正な完全五度の周波数比は 1：1.5 なので、これを12回繰り返すと 1.512≒129.746337890625 となり、7オクターヴ上（27＝128）との間にわずかな差がある」をKagefumimaruさんは執拗に取り消し続けました。私はこのような説明はあった方が良いと思います。論点の中心はそこでしょう。どこに書くかの話はその次に出てくる問題です。だからあの投票は意味がないと上で意見を表明したのです。私の考える本来の論点は『12の純正な完全五度と7オクターヴとの差』を示す数式を記事本文中に残すかどうかです。上で概出ですが小数・分数の併記でも私は構いませんよ。ただし、文系の人間にも分かりやすいtamieさんの小数での説明は残すべき。それが私の主張です。--Gruppetto（会話） 2019年7月1日 (月) 14:54 (UTC)

「私の考える本来の論点は『12の純正な完全五度と7オクターヴとの差』を示す数式を記事本文中に残すかどうかです」とおっしゃりますが、私はその点について全くどうでもいいです。ただ文脈が破綻してないことが必要だと考えています。而「小数・分数の併記」による数式というのがどのようなものなのか具体的に記述していただけないでしょうか、私にはそのようなことは不可能だと思うのですが。また再三要求したことですが小数での説明が文系の人にもわかりやすいという根拠を具体的に説明してください。--Kagefumimaru（会話） 2019年7月1日 (月) 15:08 (UTC)

『異名同音関係を利用する必要がある』だけでなく『12回の五度の連鎖が異名同音に到達する』ということの説明がなければ『12の純正な完全五度と7オクターヴとの差』という操作は理解できないと私は考えます。--Kagefumimaru（会話） 2019年7月1日 (月) 15:01 (UTC)

だったらtamieさんの書いた式の上に『12回の五度の連鎖が異名同音に到達する』ということの説明を書けば良いのにあなたのやったことはtamieさんの記述の執拗な除去ですね。--Gruppetto（会話） 2019年7月1日 (月) 15:12 (UTC)

ひとつ言っておきますが、Kagefumimaru氏は他人の発言の途中に文章を割り込ませるのはやめなさい。完全にルール違反です。--Gruppetto（会話） 2019年7月1日 (月) 15:14 (UTC)

インデントが異なるので別々の回答が必要だと考えたのですが、誤解でしたら申し訳ありません。--Kagefumimaru（会話） 2019年7月1日 (月) 15:16 (UTC)

インデントは異なっていません。途中で強制改行（＜br＞）をしているので、そのままだとインデントが頭に戻ってしまうのでインデントを揃えたものです。--Gruppetto（会話） 2019年7月2日 (火) 05:15 (UTC)

2人ともいい加減にしてください。折角議論を仕切り直したのにねちねちねちねちと……。分数小数うんぬんは「『12の純正な完全五度と7オクターヴとの差』という操作の意味と、それによって五度圏が閉じないということは説明抜きに理解できるか」が決着してからまた考えれば良いと言っているでしょう。合意する気があるんですか？ あるなら合意から遠ざかる道を進まないでください。私が第三者として議論に加わったのに意味がないじゃないですか。--610CH-405（会話） 2019年7月1日 (月) 15:23 (UTC)

（インデント戻す）勝手に議論が進みかけていましたので、私の主張をまとめます。

• 『12の純正な完全五度と7オクターヴとの差』を示す説明と数式は記事本文中に書かれてあるべきである。
• 数式は小数、分数 併記でも構わないが文系の人間にも分かりやすい小数の表記も書くべき。

--Gruppetto（会話） 2019年7月1日 (月) 15:29 (UTC)

だから、今している議論はその前段階だと何回言えばお分かりいただけますか。論点をわざわざ混乱させないでください。--610CH-405（会話） 2019年7月1日 (月) 15:32 (UTC)

はっきり言わせてもらいましょうか。「今日初めて議論を上から読みました」という方が「2人ともいい加減にしてください」とか強調文字を多用して「ねちねち」などと汚い言葉を使って何を仲裁者ぶっているのですか？？？--Gruppetto（会話） 2019年7月1日 (月) 15:34 (UTC)

返信 個人攻撃は無視します。では、気を取り直して。今は一旦、この質問 にお答えする一貫として こちらで提案していただいた論点 への解決方法の案を述べてみます。

「ニューグローヴ音楽辞典の記述 （2019年5月8日 (水) 17:55 (UTC)参照）は不十分ということでしょうか。」→ニューグローヴ音楽辞典とは、このコメントの時点の版 で唯一出典として用いられている資料のことですね。

「なぜ12音なのかが説明されていません」→これに関しては「五度圏が十二平均律を前提としていること」を出典付きで記述すれば解消できると考えます。ただ、ニューグローヴには「平均律」とあるだけで「十二平均律」とは明記されていないため（まぁ一般に平均律 = 十二平均律だし文脈からもわかるが）、これを出典として用いるには不安は残ります。ダメとは断言できませんが、「十二平均律」と明記されている資料があるのであればそちらを使うべきでしょう。Wikipedia:空が青いということに出典は要らない / Wikipedia:空が青いということに出典は要るを参照いただければと思いますが、jawp内で両方の立場があって見解の統一がなされていないということなので、安全策を取るにこしたことはありません。すなわち、誰かが「ニューグローヴを出典にするとWikipedia:空が青いということに出典は要るに違反するのでダメだ、出典無効だ」などと言い出しても、反論できない可能性が高いということです。

「なぜ異名同音の考え方を使うのかが説明できていません」→まず、上記「十二平均律を前提としている」に添った説明となるよう、「異名同音によって環が閉じないことを解消できる」ではなく、逆に「ピタゴラス音律（= 純正完全五度の積み重ね）だと環が閉じない」というロジックの説明に置き換えます。その過程で、

1. 五度圏の前提である十二平均率律において、元のC音から完全五度12個分上のB♯音は元のC音の7オクターヴ上のC音と異名同音である。
2. 1オクターヴは 2 : 1 の周波数比であり、これは十二平均率律でもピタゴラス音律でも同じである。純正完全五度は 3 : 2 の周波数比を持つ。
3. すなわち、ピタゴラス音律において、元のC音の完全五度12個分上のB♯音と元のC音の7オクターヴ上のC音は (3/2)^12 : (2/1)^7 = 3^12 : 2^19 = 531441 : 524288 の周波数比を持ち、これはピタゴラスコンマの周波数比に等しい。
4. これは、ピタゴラス音律において元のC音の完全五度12個分上のB♯音と元のC音の7オクターヴ上のC音との間では異名同音が成立しないことを意味する。
5. よって、「ピタゴラス音律（= 純正完全五度の積み重ね）だと環が閉じない」

という論理展開で説明し、ここに件の数式が出てくるわけです（表記方法の詳細は後程検討すれば良いので今こねくりまわさないように）。

「完全五度はそれぞれ純正音程よりもピタゴラスコンマの1/12だけ狭められている」→これは単に周波数比かcentかも説明する必要があるということです（両者で意味合いが全く違いますから）。--610CH-405（会話） 2019年7月1日 (月) 15:35 (UTC) 誤字訂正--610CH-405（会話） 2019年7月13日 (土) 13:29 (UTC)

『ピタゴラス音律（= 純正完全五度の積み重ね）だと環が閉じない』という説明には『五度圏は異名同音によって閉じた輪を形成している』という情報が事前に必要です。閉じた状態を規定せずに閉じない状態は規定できません。ですから『12の純正な完全五度と7オクターヴとの差がある』だけでは五度圏が閉じない説明にはなりません。それからセント値というのは周波数比ですから意味合いは同じですよ、多分セント値が一般に概数で書かれるということを指してるのだと想像しますが。--Kagefumimaru（会話） 2019年7月1日 (月) 15:51 (UTC)

コメント 「『五度圏は異名同音によって閉じた輪を形成している』という情報が事前に必要です。」→ それであれば、

• 五度圏は十二平均率律に基づいているので、完全五度上げる操作を12回繰り返すことにより、正確に元の音の7オクターヴ上の音に到達する。（これが閉じた状態のことですね）
• 平均率律であるので、「各音は無限の数の異名同音を有している」（これはニューグローヴを出典に使えます）

これらを説明に盛り込めば解決できるのではないでしょうか？

あと、セント値は周波数比ではなく、周波数比を対数で表したものです。それから、周波数比であれば単に 1/12 とは書けないでしょう。「12等分」と言葉で書く必要があるように思います。1/12 は数式と解釈される可能性がありますが、数式的な考え方をするならば12乗根になりますので。（「12等分」と言葉で書けば、セントだろうが周波数比だろうが意味合いは同じになろうかと思います。）--610CH-405（会話） 2019年7月1日 (月) 16:16 (UTC) 誤字訂正--610CH-405（会話） 2019年7月13日 (土) 13:29 (UTC)

『12の五度の連鎖を異名同音を利用して環にしたもの』というのは五度圏の本質的な定義であって、それを他の形に言い換える必要はありません。『五度圏は異名同音によって閉じた輪を形成している』という事を説明するのにWHYは意味がありません、必要なのはHOWです。--Kagefumimaru（会話） 2019年7月1日 (月) 17:14 (UTC)

おっしゃる意味がよくわかりません。具体的に説明をお願いします。私としてはWHYではなくHOWを書いたつもりです。--610CH-405（会話） 2019年7月1日 (月) 22:59 (UTC)

「なぜ異名同音の考え方を使うのか」「なぜ12音なのか」といったことを説明する必要はまったくないということです。ニューグローヴの説明方法は模範的なものと考えて問題ないはずです。--Kagefumimaru（会話） 2019年7月1日 (月) 23:03 (UTC)

いや、だからそれを出典付きで書く必要があるでしょう、現在の記事では説明されていませんから。--610CH-405（会話） 2019年7月1日 (月) 23:06 (UTC)

今は出典などは問題にしてないはずです。論点は「『12の純正な完全五度と7オクターヴとの差』という操作の意味と、それによって五度圏が閉じないということは説明抜きに理解できるか」でしょう。出典を完備した文例はすでに2019年5月31日 (金) 00:01 (UTC)に提示してあります。--Kagefumimaru（会話） 2019年7月1日 (月) 23:09 (UTC)

じゃあはい、言い方を変えましょう。出典うんぬん以前に現在の記事で説明されていないでしょう。「『12の純正な完全五度と7オクターヴとの差』という操作の意味と、それによって五度圏が閉じないということは説明抜きに理解できるか」→これが出来ていないので、これを説明できるようにするには「『12の純正な完全五度と7オクターヴとの差』という操作の意味と、それによって五度圏が閉じないということ」を読んだ人に理解できるようにするには説明をどう組み立てれば良いか考えています。んで、説明が足りないので記事に追加する必要がありますよ、追記する際は出典を付ける必要がありますが、という意味です。--610CH-405（会話） 2019年7月1日 (月) 23:15 (UTC) 下線部訂正--610CH-405（会話） 2019年7月1日 (月) 23:23 (UTC)

「『12の純正な完全五度と7オクターヴとの差』という操作の意味と、それによって五度圏が閉じないということは説明抜きに理解できるか」ということを記事で説明する必要は全くありません。--Kagefumimaru（会話） 2019年7月1日 (月) 23:19 (UTC)

すみません、言葉の選び方が悪かったです。書き直しました。--610CH-405（会話） 2019年7月1日 (月) 23:23 (UTC)

論点がずれています。今の議題はまず『五度圏は異名同音を利用して環を形成している』及び『12回の五度の連鎖が異名同音に到達する』という説明は『12の純正な完全五度と7オクターヴとの差』という操作の意味と、それによって五度圏が閉じないということの説明に不可欠か否かということです。610CH-405さんの考えはどちらなのですか。--Kagefumimaru（会話） 2019年7月1日 (月) 23:28 (UTC)

必要でしょう。『五度圏は異名同音を利用して環を形成している』『12回の五度の連鎖が異名同音に到達する』は前提条件なので、これを記述して初めて、ピタゴラス音律で環が閉じないことを導く操作の説明が意味を持つものになります。

それから、出典は2019年5月31日 (金) 00:01 (UTC) に完備されているなどと言われたので、その文案を拝見しました。これだと出典に「十二平均率律」と明記されていないのでWikipedia:空が青いということに出典は要るを元に反論される可能性がある以上、別の出典を探すのが安全ではあります（これは前述の私の考えと同じ）。それから、文案ではピタゴラス音律で環が閉じないことが唐突に説明されているので、操作方法については別途加筆する必要があるように思います。--610CH-405（会話） 2019年7月1日 (月) 23:38 (UTC) 誤字訂正--610CH-405（会話） 2019年7月13日 (土) 13:29 (UTC)

それについてTamieさんとGruppettoさんはずっと反対し続けていますが、それを納得させる方策はありますか。--Kagefumimaru（会話） 2019年7月1日 (月) 23:42 (UTC)

┌────────────────────────────────────────────────────────────────────────────────────────────────────┘ （インデント戻す）私が説明してからそのお二方から意思表示を頂いていませんが、その私の説明でご理解いただけないのであれば更なる説明を試みます。まぁ、私が言っていることは「元の記述に不備があるので、いずれにせよ『12の純正な完全五度と7オクターヴとの差』と今の文章に追記したところで説明できていないことに変わりはない、じゃあ一から説明のロジックを見直しましょう」なんですがね。--610CH-405（会話） 2019年7月1日 (月) 23:52 (UTC)

ではとりあえずTamieさんとGruppettoさんの意見を待ちましょう。--Kagefumimaru（会話） 2019年7月1日 (月) 23:57 (UTC)

ひとまず待つことに賛成します。Gruppettoさんはこのノートをご覧になっているようですが、Tamieさんは最近Wikipediaでの活動がないようなので、念のため利用者‐会話:Tamie#「ノート:五度圏」に私の意見を投稿しましたでお知らせしておきました。

賛成意見が得られた場合、または、2019年7月1日 (月) 23:52 (UTC) の私のコメントから168時間経過後の2019年7月8日 (月) 23:52 (UTC) までに異論が出なかった場合（下線部の根拠はWikipedia:合意形成です）は、合意形成と見なし、次のステップに進めればよいかな、と思います。--610CH-405（会話） 2019年7月2日 (火) 00:17 (UTC)

＞「それについてTamieさんとGruppettoさんはずっと反対し続けていますが」いいえ。それ自体について私は別に反対などしていません。上でも書きましたが、私は2019年5月5日 (日) 23:40（日本時間）の編集で『12の純正な完全五度と7オクターヴとの差』という内容を『異名同音関係を利用する必要がある』の下に移しましたが、それすらもKagefumimaruさんはバッサリ差し戻しました[5]。私が反対しているのはtamieさんの数式を取り去るKagefumimaruさんの行為です。--Gruppetto（会話） 2019年7月2日 (火) 05:00 (UTC)

ノートでの合意を得る前に本文を編集してしまう点、Gruppettoさんにも問題はあるでしょう。今後は両者ともにWikipedia:腕ずくで解決しようとしないに添って行動していただくことを願います。

また、このノートは記事の内容について話し合う場であって、利用者個人の行動について述べる場ではありません。相手の行動に不満がある場合は利用者の会話ページで改善を呼び掛けてください。

さて、本題に戻しますが、Gruppettoさんにおかれましては、私の提案内容への異論は無いという認識でよろしいでしょうか？ --610CH-405（会話） 2019年7月2日 (火) 05:20 (UTC)

＞「このノートは記事の内容について話し合う場であって、利用者個人の行動について述べる場ではありません」両者は関連があります。言い換えれば、tamieさんの数式を記事から取り除くのに反対、という意味です。610CH-405さんの提案内容については別に異論はありません。インデントですが、あのままだと私のKagefumimaruさんへの返答とあなたの書き込みが同じ位置になってしまいますが、それでも良いのでしたら構いませんよ。--Gruppetto（会話） 2019年7月2日 (火) 05:31 (UTC)

2019年5月15日 (水) の議論にあるように、Gruppettoさんは『12の純正な完全五度と7オクターヴとの差』という操作は説明抜きにその意味を理解できると主張し続けていましたが、これらはすべて撤回するということで良いですか。--Kagefumimaru（会話） 2019年7月2日 (火) 09:32 (UTC)

私の提案に賛同することは必ずしも2019年5月15日 (水) の議論での主張を撤回するということにはなりません。折角第一段階の合意に向かっているのです。発言撤回などという今重要でない事項を持ち込まないでいただけますか。--610CH-405（会話） 2019年7月2日 (火) 10:05 (UTC)

「『五度圏は異名同音を利用して環を形成している』及び『12回の五度の連鎖が異名同音に到達する』という説明は『12の純正な完全五度と7オクターヴとの差』という操作の意味と、それによって五度圏が閉じないということの説明に不可欠である」という主張と「『12の純正な完全五度と7オクターヴとの差』という操作は説明抜きにその意味を理解できる」という主張は矛盾します。どちらを選択するのかはっきりさせることが議論を次の段階に進めるために必要です。--Kagefumimaru（会話） 2019年7月2日 (火) 10:14 (UTC)

┌────────────────────────────────────────────────────────────────────────────────────────────────────┘ （インデント戻す）続きは利用者‐会話:Kagefumimaruにて返答します。--610CH-405（会話） 2019年7月2日 (火) 10:26 (UTC)

早速議論が長大化していて、私が思っている「私の提案」と、私以外の方の思っている「610CH-405の提案」が食い違っている可能性があるので、2019年7月1日 (月) 13:57 (UTC) のコメントを要点ごとにまとめます。

1. 『五度圏は異名同音を利用して環を形成している』及び『12回の五度の連鎖が異名同音に到達する』という説明は『12の純正な完全五度と7オクターヴとの差』という操作の意味と、それによって五度圏が閉じないということの説明に不可欠である
2. 並行して記事の内容も充実させるべき
3. 元の説明が不十分だから、一から書き直しましょう

というのが私の提案でした。認識のすれ違いが生じていたとすれば申し訳ございません。確認のため、今一度賛成 / 反対を表明していただければありがたいです。なお、1. - 3. の各項目ごとに賛成 / 反対を表明していただいても構いません表明してくださるようお願いします。--610CH-405（会話） 2019年7月2日 (火) 10:42 (UTC) お願いを若干変更--610CH-405（会話） 2019年7月2日 (火) 10:49 (UTC)

賛成 すべての項目に賛成します。--Kagefumimaru（会話） 2019年7月2日 (火) 10:47 (UTC)

コメント1. については、「その説明は必ずしも不可欠ではないが、わかりやすさの面からあって良い。その説明を加えることには特に反対していない」が私の立場です。矛盾はありません。--Gruppetto（会話） 2019年7月2日 (火) 12:13 (UTC)

ありがとうございます。2. と 3. についてはいかがでしょうか？ --610CH-405（会話） 2019年7月2日 (火) 12:15 (UTC)

不可欠ではないという具体的な理由を説明してください。これは説明という行為に関する根本的な問題です。--Kagefumimaru（会話） 2019年7月2日 (火) 12:20 (UTC)

合意へ進む上で、その説明は全く不要だと思いますが。--Gruppetto（会話） 2019年7月2日 (火) 12:25 (UTC)

返信 (Kagefumimaruさん宛) あっても構わないと同意していただいているんだからそれでもういいでしょう。あなたのその発言は記事の発展に無意味であるどころか、Wikipedia:妨害的編集#いつまでも納得しないに抵触する可能性があります。--610CH-405（会話） 2019年7月2日 (火) 12:27 (UTC)

Gruppettoさんの主張は記事の記述に論理的整合性が不要だと断じているに等しいことです。これはこの先記事の内容についてどのような議論を行うにしても障害になります。--Kagefumimaru（会話） 2019年7月2日 (火) 12:41 (UTC)

Gruppettoさんは「論理的整合性が不要だ」とは断じていないでしょう。『五度圏は異名同音を利用して環を形成している』及び『12回の五度の連鎖が異名同音に到達する』という説明は『12の純正な完全五度と7オクターヴとの差』という操作の意味と、それによって五度圏が閉じないということの説明はなくても論理的整合性は確保できるが、説明としてはあっても構わないと仰っているように推察します。むしろ、Kagefumimaruさんが相手の発言を無理のある推論により曲解し、それに基づいた言動を行っていることが議論の障害となっていることをそろそろ自覚してください。--610CH-405（会話） 2019年7月2日 (火) 12:48 (UTC)

そうならば「12の純正な完全五度と7オクターヴとの差』という操作の意味と、それによって五度圏が閉じないということの説明はなくても論理的整合性は確保できる」ということの理由を説明するのに何の問題もないはずです。--Kagefumimaru（会話） 2019年7月2日 (火) 12:50 (UTC)

Kagefumimaruさんがこんなこと を仰るので提案内容を再度変更します。変更したところで記事の内容に影響は及びませんので、はっきり言ってこれは無駄な作業です。しかし、これをやれば合意が成立する、事が収まるというなら、私はやります。

1. 『五度圏は異名同音を利用して環を形成している』及び『12回の五度の連鎖が異名同音に到達する』という説明を本文に記載する。また、これを『12の純正な完全五度と7オクターヴとの差』という操作の意味と、それによって五度圏が閉じないということの説明の根拠に用いる。
2. 並行して記事の内容も充実させるべき
3. 元の説明が不十分だから、一から書き直しましょう

お手数ですがGruppettoさん、今一度この3つそれぞれについて賛否を表明していただければ幸いです。--610CH-405（会話） 2019年7月2日 (火) 13:11 (UTC)

1. については賛成です。2. 3.についても反対していません。ただし、議論の発端となったtamieさんの小数による数式は一般の人にも分かりやすいので記事内にあるべきです。もちろん分数との併記でも構いません。例えば、kagefumimaruさんの2019年5月31日 (金) 00:01 (UTC)案にtamieさんの数式を加えるのでも良いでしょう。

五度圏（ごどけん、英語：circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである(注1)。

五度圏は F♯/G♭ や D♯/E♭ といった異名同音関係を利用することで環を形成しており、これは一般に平均律を前提としている(注1)。純正な完全五度に基づくピタゴラス音律では異名同音は一致しないため閉じた環を形成できない(注1)。例えばE♭を起点として完全五度を12回上方向に堆積すると異名同音関係にあるD♯が得られる (E♭-B♭-F-C-G-D-A-E-B-F♯-C♯-G♯-D♯)、しかし純正な完全五度による場合、周波数比は 1：1.5 なので、これを12回繰り返すと 1.5¹²≒129.746337890625 となり、7オクターヴ上（2⁷＝128）よりもわずかに高くなる。このため、このD♯とE♭は正確なユニゾンやオクターヴ関係にならずピタゴラスコンマの差が生じる(注2)。 平均律の完全五度は純正音程よりも1/12ピタゴラスコンマだけ狭められているため、異名同音が一致し、一様な五度によって閉じた五度圏を形成することができる(注3)。

五度圏はある調から他の調への「遠隔度」を説明するのに用いられる(注1)。例えばト長調に対し五度圏上で隣接する5つの調（ホ短調、ニ長調、ロ短調、ハ長調、イ短調）は和声的に近い関係にある近親調である（注4）。一方、五度圏上で最も離れた嬰ハ長調とは疎遠であり、その音階上の三和音に共通するものが1つもない（注5）。

注1：William Drabkin, “Circle of fifths,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001). 注2：Margo Schulter, Pythagorean Tuning and Medieval Polyphony, 1998. 注3：Mark Lindley, “Temperaments,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001). 注4：Ryan J. Thomson, A Folk Musicians Working Guide to Chords, Keys, Scales, and More, Captain Fiddle Publications, 1991. 注5：“Circle of fifths,” in The New Oxford Companion to Music, ed. by Denis Arnold, Oxford University Press, 1983.

--Gruppetto（会話） 2019年7月2日 (火) 13:38 (UTC)一部修正--Gruppetto（会話） 2019年7月2日 (火) 13:41 (UTC)一部修正Gruppetto（会話） 2019年7月13日 (土) 05:00 (UTC)

反対です。そのような表記方法の典拠が不明です。参考に私の案を示します。

五度圏（ごどけん、英語：circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである(注1)。

五度圏は F♯/G♭ や D♯/E♭ といった異名同音関係を利用することで環を形成しており、これは一般に平均律を前提としている(注1)。純正な完全五度に基づくピタゴラス音律では異名同音は一致しないため閉じた環を形成できない(注1)。例えばE♭を起点として完全五度を12回上方向に堆積すると異名同音関係にあるD♯が得られる (E♭-B♭-F-C-G-D-A-E-B-F♯-C♯-G♯-D♯)、しかし純正な完全五度(3:2)による場合、このD♯とE♭は正確なユニゾンやオクターヴ関係にならない。すなわち12の純正な完全五度 (3:2)^12 と7つのオクターヴ (2:1)^7 には 531441:524288 (約23.46セント) の差があり、この差をピタゴラスコンマと呼ぶ(注2)。平均律の完全五度は純正音程よりも1/12ピタゴラスコンマだけ狭められているため、異名同音が一致し、一様な五度によって閉じた五度圏を形成することができる(注3)。

五度圏はある調から他の調への「遠隔度」を視覚化するのに用いられる(注1)。例えばト長調に対し五度圏上で隣接する5つの調（ホ短調、ニ長調、ロ短調、ハ長調、イ短調）は和声的に近い関係にある近親調である（注4）。一方、五度圏上で最も離れた嬰ハ長調とは和声的に遠い関係にあり、その音階上の三和音に共通するものが1つもない（注5）。

注1：William Drabkin, “Circle of fifths,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 5, pp. 866-867. 注2：Margo Schulter, Pythagorean Tuning and Medieval Polyphony,(http://www.medieval.org/emfaq/harmony/pyth.html ), 1998. 注3：Mark Lindley, “Temperaments,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 25, pp. 248-269. 注4：Ryan J. Thomson, A Folk Musicians Working Guide to Chords, Keys, Scales, and More, Captain Fiddle Publications, 1991, p. 52. 注5：“Circle of fifths,” in The New Oxford Companion to Music, ed. by Denis Arnold, Oxford University Press, 1983, vol. 1, p. 399.

--Kagefumimaru（会話） 2019年7月2日 (火) 13:46 (UTC)

分数だの小数だのは今の合意に関係ない、後で検討しましょうと何度言えばわかりますか。

話を戻しまして、ひとまず、Gruppettoさんは私の新提案への異論はないようです。Kagefumimaruさんに私の新提案に同意いただき、なおかつ新提案から168時間後の2019年7月9日 (火) 13:11 (UTC) までにTamieさんから異論がなければ合意形成と見なそうと考えています。

Kagefumimaruさん、私の新提案の各項目への賛否をコメントいただければ幸いです。--610CH-405（会話） 2019年7月2日 (火) 13:53 (UTC)

再びすべての項目に賛成します。--Kagefumimaru（会話） 2019年7月2日 (火) 13:54 (UTC)

報告 Tamieさんの会話ページにお知らせしてきました 。2019年7月9日 (火) 13:11 (UTC) までに異論が寄せられない場合、または賛同コメントを頂いた場合はその段階で合意形成と見なします。合意形成が成立するまでお二方には少しお待ちいただくことにはなりますが、Wikipediaの性質上仕方ないことですので予めご了承いただきたく存じます。本件の議論へのご協力ありがとうございました。引き続きまた1週間後 (?) 以降よろしくお願い致します。--610CH-405（会話） 2019年7月2日 (火) 14:09 (UTC)

1週間が経過しましたので合意が形成されたと考え議論を先に勧めます。Gruppettoさんは「小数による数式は一般の人にも分かりやすい」と主張し続けていますが、その具体的な理由については答えることができていません。Wikipedia:論争の解決に従えば具体的な根拠を示さずに意見を主張することは正しい議論の方法ではありません。Gruppettoさんは「小数による数式は一般の人にも分かりやすい」という具体的な理由を説明してください。説明ができないのであればそれは根拠のない主張と結論付けられます。--Kagefumimaru（会話） 2019年7月13日 (土) 02:03 (UTC)

編集が競合してしまいましたが、そのまま返答を書かせていただきます。上の例で言えば、^ という記号の理解には一定以上の数学のレベルが必要です。小数の式の方がわかりやすいですね。また、現実に分かりやすいと言っている人がいるのに、その理由を具体的に説明せよと執拗に迫るのは馬鹿げています。「あなたが蕎麦よりうどんが好きな理由を具体的に説明せよ」と言っているのと同じです。だから別に併記でも良いと私は言っています。Gruppetto（会話） 2019年7月13日 (土) 04:45 (UTC)

コメント 提案 来るのが遅くなりましたが、合意形成ですね。お疲れさまでした。さて、Kagefumimaruさん、次の論点は本当にそこで良いのでしょうか？ 私はそうは思いません。現時点では、あなたが勝手にそれが次の論点だと考えているだけのように思います。今回の合意事項は 1. から 3. に分かれていますが、この合意内容に基づいて議論を発展させるべきでしょう。そうでなければ、この数か月のような様相の論争を繰り返すだけになります。一旦節を分け、次の論点がどこか出し合うべきだと考えます（#論点整理のような節名でよいでしょう）。その上で、個々の論点の中身や詳細について話し合うことを禁じ、ひとまず論点の整理（次に話し合うべきはどこなのかの議論）に集中する、という形をとることを提案します。--610CH-405（会話） 2019年7月13日 (土) 04:40 (UTC) 一部追記--610CH-405（会話） 2019年7月13日 (土) 04:53 (UTC)

論点の整理に賛成します。そして議論するべき論点は「純正音程を整数比で表記すべきか、小数で表記すべきか」であると考えます。現在他に意見の対立がみられる点がありません。--Kagefumimaru（会話） 2019年7月13日 (土) 06:36 (UTC)

ありがとうございます。（議論を行う対象は意見が対立している点のみではありませんので、その点の認識はお願いします。）

さて、Gruppettoさん、論点の整理の是非についていかがお考えでしょうか？ --610CH-405（会話） 2019年7月13日 (土) 07:24 (UTC)

意見が対立している点以外について私は議論を行うつもりはありません。「議論を発展させるべき」という考えには全く反対します。議論は収束させ解決させるものです、議論を拡散させるような考えには賛成できません。--Kagefumimaru（会話） 2019年7月13日 (土) 07:35 (UTC)

ご発言の意図が分かりかねますが、私は議論を拡散させようとしていません。今回の合意事項に基づき議論を進めましょうと言っているだけです。また、議論の対象は意見が対立している点のみではなく、例えば「記事の充実の方法をどうするか」「説明を一から書き直すが、文面はどうするか」などを想定しています。参加するつもりがないなら参加していただかなくても構いませんが、いずれにせよ今私が示したような議論を行わないことには今回の合意事項を記事内容に反映できませんので、該当する議論は行う予定です。--610CH-405（会話） 2019年7月13日 (土) 07:59 (UTC)

論点が決定するまでとりあえず併記案を示しておきます。これで合意が得られるのなら私には他に特に議論することはありません。

五度圏（ごどけん、英語：circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである(注1)。

五度圏は F♯/G♭ や D♯/E♭ といった異名同音関係を利用することで環を形成しており、これは一般に平均律を前提としている(注1)。純正な完全五度に基づくピタゴラス音律では異名同音は一致しないため閉じた環を形成できない(注1)。例えばE♭を起点として完全五度を12回上方向に堆積すると異名同音関係にあるD♯が得られる (E♭-B♭-F-C-G-D-A-E-B-F♯-C♯-G♯-D♯)、しかし純正な完全五度 (3:2) による場合、このD♯とE♭は正確なユニゾンやオクターヴ関係にならない。すなわち12の純正な完全五度 $(3:2)^{12}=129.746337890625$ と7つのオクターヴ $(2:1)^{7}=128$ には $531441:524288=1.0136432647705078125$ (約23.46セント) の差があり、この差をピタゴラスコンマと呼ぶ(注2)。平均律の完全五度は純正音程よりも1/12ピタゴラスコンマだけ狭められているため、異名同音が一致し、一様な五度によって閉じた五度圏を形成することができる(注3)。

五度圏はある調から他の調への「遠隔度」を視覚化するのに用いられる(注1)。例えばト長調に対し五度圏上で隣接する5つの調（ホ短調、ニ長調、ロ短調、ハ長調、イ短調）は和声的に近い関係にある近親調である（注4）。一方、五度圏上で最も離れた嬰ハ長調とは和声的に遠い関係にあり、その音階上の三和音に共通するものが1つもない（注5）。

注1：William Drabkin, “Circle of fifths,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 5, pp. 866-867. 注2：Margo Schulter, Pythagorean Tuning and Medieval Polyphony,(http://www.medieval.org/emfaq/harmony/pyth.html ), 1998. 注3：Mark Lindley, “Temperaments,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 25, pp. 248-269. 注4：Ryan J. Thomson, A Folk Musicians Working Guide to Chords, Keys, Scales, and More, Captain Fiddle Publications, 1991, p. 52. 注5：“Circle of fifths,” in The New Oxford Companion to Music, ed. by Denis Arnold, Oxford University Press, 1983, vol. 1, p. 399.

--Kagefumimaru（会話） 2019年7月13日 (土) 07:37 (UTC) （数値修正）--Kagefumimaru（会話） 2019年7月13日 (土) 07:46 (UTC)

では私は次のように提案します。ほとんど同じものですので、違う部分のみをあえて太字で示しますが、実際の本文では太字にはしません。いかがでしょうか？

五度圏（ごどけん、英語：circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである(注1)。

五度圏は F♯/G♭ や D♯/E♭ といった異名同音関係を利用することで環を形成しており、これは一般に平均律を前提としている(注1)。純正な完全五度に基づくピタゴラス音律では異名同音は一致しないため閉じた環を形成できない(注1)。例えばE♭を起点として完全五度を12回上方向に堆積すると異名同音関係にあるD♯が得られる (E♭-B♭-F-C-G-D-A-E-B-F♯-C♯-G♯-D♯)、しかし純正な完全五度 (3:2) による場合、このD♯はE♭よりもわずかに高くなり、正確なユニゾンやオクターヴ関係にならない。すなわち12の純正な完全五度 $(3:2)^{12}=129.746337890625$ と7つのオクターヴ $(2:1)^{7}=128$ には $531441:524288=1.0136432647705078125$ (約23.46セント) の差があり、この差をピタゴラスコンマと呼ぶ(注2)。平均律の完全五度は純正音程よりも1/12ピタゴラスコンマだけ狭められているため、異名同音が一致し、一様な五度によって閉じた五度圏を形成することができる(注3)。

五度圏はある調から他の調への「遠隔度」を視覚化するのに用いられる(注1)。例えばト長調に対し五度圏上で隣接する5つの調（ホ短調、ニ長調、ロ短調、ハ長調、イ短調）は和声的に近い関係にある近親調である（注4）。一方、五度圏上で最も離れた嬰ハ長調とは和声的に遠い関係にあり、その音階上の三和音に共通するものが1つもない（注5）。

注1：William Drabkin, “Circle of fifths,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 5, pp. 866-867. 注2：Margo Schulter, Pythagorean Tuning and Medieval Polyphony,(http://www.medieval.org/emfaq/harmony/pyth.html ), 1998. 注3：Mark Lindley, “Temperaments,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 25, pp. 248-269. 注4：Ryan J. Thomson, A Folk Musicians Working Guide to Chords, Keys, Scales, and More, Captain Fiddle Publications, 1991, p. 52. 注5：“Circle of fifths,” in The New Oxford Companion to Music, ed. by Denis Arnold, Oxford University Press, 1983, vol. 1, p. 399.

--Gruppetto（会話） 2019年7月13日 (土) 08:09 (UTC)

反対します。D♯はE♭よりわずかどころではなく(3:2)^12も高いです。書くとしたら「このD♯は元のE♭の7オクターヴ上のE♭よりわずかに高い音高になる」としなければなりません。またそのような記述が典拠[6]にありません。--Kagefumimaru（会話） 2019年7月13日 (土) 08:18 (UTC)

ピッチクラスとしてはわずかに高いだけですよね？Gruppetto（会話） 2019年7月13日 (土) 08:32 (UTC)

この場合D♯やE♭がピッチクラスであることは自明ではありません。ピッチクラスの概念は説明する方には便利ですが予備知識のない読者には優しくないので今回の文案からは排除しています。「このD♯は元のE♭の7オクターヴ上のE♭よりわずかに高い音高になる」としてこの部分は出典なしの記述とすることでどうでしょうか。--Kagefumimaru（会話） 2019年7月13日 (土) 08:50 (UTC)

なおその場合「正確なユニゾンやオクターヴ関係にならない。」という記述は駄目になるのでこれは除去することになります。--Kagefumimaru（会話） 2019年7月13日 (土) 08:53 (UTC)

わかりました。では、「わずかに高くなる」という表記は無くとも良いので、Kagefumimaruさんが2019年7月13日 (土) 07:46 (UTC)、日本時間16:46で示した案に合意します。--Gruppetto（会話） 2019年7月13日 (土) 12:58 (UTC)

忘れておりましたが 2019年7月1日 (月) 15:35 (UTC)に610CH-405から提示された当文案に関する懸念について回答しておきます。まず「十二平均律」とすべきではないか?ということですが、まずニューグローヴの Equal temperament の定義は "A tuning of the scale based on a cycle of 12 identical 5ths and with the octave divided into 12 equal semitones..." となっており、終わりの方に "Occasionally the term "equal temperament" has been used loosely as a generic term for divisions of the octave into any number of equal parts." という事も書かれていますが、これはあくまで例外的な用法とされています。したがって特定の文脈以外で平均律を十二平均律以外の意味に読むことは異常であり、それに対する配慮は不要と考えられます。ただ日本語の「平均律」は必ずしも Equal temperament の訳ではなく temperament を意味する用法が存在し、古い文献には「不等分平均律」や「中全音平均律」といった用語が出てきたりもするのですが、この場合も「平均律」は一般に「十二等分平均律」のことだとされているので問題ないでしょう。それからコンマの分割を示すのに分数を使うことですが、これはごく一般的な慣習ですので (ex. 1/4sc meantone) セントか比かということを気にする必要はないと思います。--Kagefumimaru（会話） 2019年7月13日 (土) 09:48 (UTC)

ありがとうございます。私も忘れかけておりました。出典に「一般には十二平均率律を指す」という趣旨の記述があるようであれば、前述の私の懸念は払拭されたと考えます。また、コンマの分割を示すのに分数を使うことについては、私の考えすぎと言われればそこまでですが、厳密性を求めるというか安全策をとるならば、具体的な数値を括弧書きもしくは注釈で示す方法も考えられますので、頭の片隅にでも入れておいていただければと思います。--610CH-405（会話） 2019年7月13日 (土) 09:57 (UTC) 誤字訂正--610CH-405（会話） 2019年7月13日 (土) 13:29 (UTC)

コメント 繰り返し恐縮ですが、Gruppettoさん、論点の整理の是非についていかがお考えでしょうか？ --610CH-405（会話） 2019年7月13日 (土) 09:18 (UTC)

610CH-405さん、とりあえず今は私とKagefumimaruさんの間では論点は一致しています。Gruppetto（会話） 2019年7月13日 (土) 09:23 (UTC)

あなた方2人だけで議論しているわけではありません。少なくとも、私とあなた方2人では次の論点をどうすべきかの意見は一致していません。繰り返しますが、Gruppettoさん、論点の整理の是非についていかがお考えでしょうか？

なお、万が一「どうしても分数小数問題を解決してからでなければ次に進めない」とお二人が仰るのであればまた考えますが、仮にそうなった場合は「記事の内容の充実」「説明を一から書き直す」との整合性を取りながら進める必要があるでしょう。私は以前申し上げた通り英語版からの翻訳もした方がよいのではないか、という考えがありますので、それも考慮いただければと考えている次第です。--610CH-405（会話） 2019年7月13日 (土) 09:36 (UTC)

すいませんが私はこれからちょっとした用事がございますので、回答を数時間お待ちください。--Gruppetto（会話） 2019年7月13日 (土) 09:57 (UTC)

610CH-405さん、とりあえず以前から議論していたは私とKagefumimaruさんでまず合意し、その上で610CH-405さんに更なる意見があれば改めて具体的に示して頂く、という形でお願いします。Gruppetto（会話） 2019年7月13日 (土) 13:07 (UTC)

コメント ありがとうございます。ひとまずお二人は合意に近づいているようですね。Kagefumimaruさんがお二人の合意後に私 (610CH-405) が具体的な意見を述べる形式で良い旨表明いただければ、私もその方式で大丈夫です。

（合意に大きく影響するような意見はないのでざっと考えていることを書きます。）現在ご提示頂いている文面ならば説明の論理性は十分だと私は考えているので、「説明を一から書き直す」という点はクリアできています。また、この文章であれば「記事の内容の充実」を後からやろうとしても上手く処理できそうです（仮に「翻訳」するとしても該当節のみこの文面のままにしておけばよいかと）。あとは数式の挿入の仕方や表記ガイド関係で若干気になる点があるのみです。ひとまずKagefumimaruさんの反応を待ちたいと思います。--610CH-405（会話） 2019年7月13日 (土) 13:23 (UTC)

2019年7月13日 (土) 07:46 (UTC)案で合意が得られたようですので、それで記事を置き換えようとおもいますが、一つ忘れていたことがあります、図です。Tamieさんの編集前は上に表示する五度圏の図は英語版と同じものを使用していました[7]、現状は上と下で同じものが表示されていて無駄だと思うので元に戻したほうが良いと思うのですが。--Kagefumimaru（会話） 2019年7月13日 (土) 22:27 (UTC)

コメント 「現状は上と下で同じものが表示されていて無駄だと思うので元に戻したほうが良いと思うのですが。」→すみません、どういうことでしょうか？

さて、概ねKagefumimaruさんの案で同意しますが、何箇所か気になる点があるので以下に修正案を示します。何なりとコメントください。

五度圏（ごどけん、英語: circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである (注1)。

五度圏は F♯ / G♭ や D♯ / E♭ といった異名同音関係を利用することで環を形成しており、これは一般に十二平均律を前提としている (注1)。純正な完全五度に基づくピタゴラス音律では、異名同音は異なるピッチを持つ音として区別されるため閉じた環を形成できない (注1)。例えば、E♭ を起点として完全五度を12回上方向に堆積すると異名同音関係にある D♯ が得られるが (E♭ - B♭ - F - C - G - D - A - E - B - F♯ - C♯ - G♯ - D♯)、この2音は十二平均律において同一のピッチを持つ。しかし、純正な完全五度（周波数比 3:2）に基づくピタゴラス音律による場合、この D♯ と E♭ は正確なユニゾンやオクターヴ関係にならない。すなわち、12の純正な完全五度の周波数比

$\left({\frac {3}{2}}\right)^{12}=129.746337890625$

と7つのオクターヴの周波数比

$\left({\frac {2}{1}}\right)^{7}=128$

の間には

${\frac {\left({\frac {3}{2}}\right)^{12}}{\left({\frac {2}{1}}\right)^{7}}}={\frac {531441}{524288}}=1.0136432647705078125$

の差が生じ、この差の大きさをセント値で表すと約23.46セントである。また、この差をピタゴラスコンマと呼ぶ (注2)。一方、十二平均律の完全五度は純正音程よりも 1/12 ピタゴラスコンマだけ狭められているため、異名同音同士のピッチは一致し、一様な完全五度によって閉じた五度圏を形成することができる (注3)。

五度圏はある調から他の調への「遠隔度」を視覚化するのに用いられる (注1)。例えばト長調に対し五度圏上で隣接する5つの調（ホ短調、ニ長調、ロ短調、ハ長調、イ短調）は和声的に近い関係にある近親調である (注4)。一方、五度圏上で最も離れた嬰ハ長調とは和声的に遠い関係にあり、その音階上の三和音に共通するものが1つもない (注5)。

注1：William Drabkin, “Circle of fifths,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 5, pp. 866-867. 注2：Margo Schulter, Pythagorean Tuning and Medieval Polyphony,(http://www.medieval.org/emfaq/harmony/pyth.html ), 1998. 注3：Mark Lindley, “Temperaments,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 25, pp. 248-269. 注4：Ryan J. Thomson, A Folk Musicians Working Guide to Chords, Keys, Scales, and More, Captain Fiddle Publications, 1991, p. 52. 注5：“Circle of fifths,” in The New Oxford Companion to Music, ed. by Denis Arnold, Oxford University Press, 1983, vol. 1, p. 399.

まず、比と小数を等号で結ぶことはできないため、比を分数に置換しました。その上で、数学記事等を参考に数式の挿入位置を変更し、それに伴い前後の文脈を少し調整しました。その他、リンクやスタイルの調整、曖昧な表現の修正を行ってみました。--610CH-405（会話） 2019年7月14日 (日) 04:36 (UTC)

「現状は上と下で同じものが表示されていて」というのは現状右上に表示されている五度圏の画像と下に表示されているテンプレートの画像が重複しているということです、610CH-405さんの閲覧環境ではどのように見えているのでしょうか。提案された文案ですが、まず「十二平均律」というのは上で述べたように、53平均律等とどうしても区別する必要がある場面以外ではなるべく使用すべきではありません、ここではそのような問題があるとは考えられません。「十二平均律」というのは慣用的な用語であって、あまりフォーマルなものではないのです。それから比と小数は等号で結ぶことができます、「比の値」というのは小学校で履修するはずです。それからあくまで余談に過ぎないピタゴラスコンマの算出の数式をこのように目立たせることは記事の本題を見失わせるものと思われるので、このような表記には反対します。--Kagefumimaru（会話） 2019年7月14日 (日) 05:24 (UTC)

「この2音は十二平均律において同一のピッチを持つ」という記述は誤りです、完全五度を12回上方向に堆積した先の音が同じピッチのはずがありません。この場合は「この2音は同一のピッチクラス」にあるとすれば正しいですが、前述の通り私はピッチクラスという概念を持ち出すのは予備知識のない読者に不親切なので避けるべきだと考えます。--Kagefumimaru（会話） 2019年7月14日 (日) 05:46 (UTC)

返信 「610CH-405さんの閲覧環境ではどのように見えているのでしょうか。」 → なるほど、テンプレートですか。モバイル版では表示できませんので、現状のままの表示で維持すべきと考えます。

「53平均律等とどうしても区別する必要がある場面以外ではなるべく使用すべきではありません」 → なるべく使用すべきでない根拠がわかりません。というか、この場面では区別したほうが明確でしょう。そもそも、読者が「一般に『平均律』とは『十二平均律』を指す」という前提条件を知らない可能性も考慮して執筆する必要すらあります。

「『十二平均律』というのは慣用的な用語であって、あまりフォーマルなものではないのです。」 → CiNii論文検索で日本の論文を検索したところ、「"十二平均律"」が47件、「"12平均律"」が77件で合わせて124件でした。一方、「"平均律" -"十二平均律" -"12平均律"」は532件でした。後者の結果には「53平均律」や「五十三平均律」も含まれるため多くなって当然ですが、この数の用例を以ってフォーマルでないというのはもはや無理があるのではないでしょうか。ちなみに「"平均律" -"12平均律" -"十二平均律" -"53平均律" -"五十三平均律"」としてみたところ、112件となりました。まとめますと、「12平均律」または「十二平均律」の用例が計124件、「平均律」単体および十二平均律・五十三平均律以外の「平均律」の用法は112件ということになります。

「比と小数は等号で結ぶことができます、『比の値』というのは小学校で履修するはずです。」 → 比の値の表し方というのは、例えば「3:2 の比の値は 1.5」のように表現するのであって、教科書等ではこの表記を採用していました。「3:2 = 1.5」という表記は見たことがありません（むしろ、間違いであると習いました）。

「あくまで余談に過ぎないピタゴラスコンマの算出の数式をこのように目立たせることは記事の本題を見失わせる」 → であれば、数式はすべて脚注に表示することを提案します。

「『この2音は同一のピッチクラス』にあるとすれば正しいですが、」 → これは失礼、私の間違いです。しかし、「異名同音が一致する」「異名同音が一致しない」という表現も何を以って「一致」と為すのか不明確であるため、それこそ読者に不親切ではないでしょうか？ ピッチクラスというようにリンクを貼れば問題ないとは思いますが、以下に示す案では、ひとまずどちらの表現を用いることも回避してみました。

というわけで、現時点での妥協案です。

五度圏（ごどけん、英語: circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである (注1)。

五度圏は F♯ / G♭ や D♯ / E♭ といった異名同音関係を利用することで環を形成しており、これは一般に十二平均律を前提としている (注1)。純正な完全五度に基づくピタゴラス音律では、異名同音はユニゾンやオクターヴ関係にないため閉じた環を形成できない (注1)。例えば、E♭ を起点として完全五度を12回上方向に堆積すると異名同音関係にある D♯ が得られるが (E♭ - B♭ - F - C - G - D - A - E - B - F♯ - C♯ - G♯ - D♯)、この2音は十二平均律においてユニゾンやオクターヴ関係を有する。しかし、純正な完全五度（周波数比 3:2）に基づくピタゴラス音律による場合、この D♯ と E♭ は正確なユニゾンやオクターヴ関係にならない。すなわち、12の純正な完全五度 (脚注1) と7つのオクターヴ (脚注2) の間には $531441/524288=1.0136432647705078125...$ (脚注3) の差が生じ、この差の大きさをセント値で表すと約23.46セントである。また、この差をピタゴラスコンマと呼ぶ (注2)。一方、十二平均律の完全五度は純正音程よりも 1/12 ピタゴラスコンマだけ狭められているため、異名同音はユニゾンやオクターヴ関係を有し、一様な完全五度によって閉じた五度圏を形成することができる (注3)。

五度圏はある調から他の調への「遠隔度」を視覚化するのに用いられる (注1)。例えばト長調に対し五度圏上で隣接する5つの調（ホ短調、ニ長調、ロ短調、ハ長調、イ短調）は和声的に近い関係にある近親調である (注4)。一方、五度圏上で最も離れた嬰ハ長調とは和声的に遠い関係にあり、その音階上の三和音に共通するものが1つもない (注5)。

注1：William Drabkin, “Circle of fifths,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 5, pp. 866-867.

注2：Margo Schulter, Pythagorean Tuning and Medieval Polyphony,(http://www.medieval.org/emfaq/harmony/pyth.html ), 1998.

注3：Mark Lindley, “Temperaments,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 25, pp. 248-269.

注4：Ryan J. Thomson, A Folk Musicians Working Guide to Chords, Keys, Scales, and More, Captain Fiddle Publications, 1991, p. 52.

注5：“Circle of fifths,” in The New Oxford Companion to Music, ed. by Denis Arnold, Oxford University Press, 1983, vol. 1, p. 399.

脚注1：周波数比 $\left({\frac {3}{2}}\right)^{12}=129.746337890625$

脚注2：周波数比 $\left({\frac {2}{1}}\right)^{7}=128$

脚注3：${\frac {\left({\frac {3}{2}}\right)^{12}}{\left({\frac {2}{1}}\right)^{7}}}={\frac {531441}{524288}}=1.0136432647705078125...$

--610CH-405（会話） 2019年7月14日 (日) 06:41 (UTC)

私の文案のどこにどのような理由で反対なのかを1箇所づつ論点を定めて議論をしていただくことを希望します、一度にいろいろな点を変更して文案を示されても議論はまとまりません。まず「モバイル版では表示できませんので、現状のままの表示で維持すべきと考えます」というのはどういうことでしょうか、モバイルユーザー以外の都合は無視すべきだというですか。--Kagefumimaru（会話） 2019年7月14日 (日) 06:49 (UTC)

直前のコメントで述べた通りです。また、それに基づいて妥協案を示せば上記のようになるということです。直前の私のコメントを引用して反応していただければ良いです。そうすれば、さらに原案に近づけたもので妥協案を示すことになるかもしれません。

「モバイルユーザー以外の都合は無視すべきだというですか」→ どういうことでしょうか、モバイルユーザーの都合は無視すべきだというのですか？ 本文とテンプレート両方に表示しておけばよかろう、ということです。まぁ、そもそもテンプレートの挿入位置が誤っていますが。--610CH-405（会話） 2019年7月14日 (日) 06:57 (UTC)

PCブラウザでの表示では同じ画像が表示されて無駄です、逆に同じ画像を表示させなければならない理由とは何でしょうか。また本文での説明は音名をアルファベットで表記しているので五度圏の画像もアルファベットのものが用意されていたほうが良いと考えます。--Kagefumimaru（会話） 2019年7月14日 (日) 07:05 (UTC)

あ、今仰っている意味を把握しました。本文中の画像はアルファベット表記のものに変更して差し支えないと思います。--610CH-405（会話） 2019年7月14日 (日) 07:07 (UTC)

┌────────────────────────────────────────────────────────────────────────────────────────────────────┘ 次に「十二平均律」ですが、この用語は私が以前調査した限りでは日本語の音楽事典にはけして出てきません。調査した資料は以下のとおりです。

• 白眉社『白眉音楽辞典』大正13年
• 白眉社『大楽典』昭和4年
• 平凡社『大百科事典』昭和8年
• 冨山房『國民百科大辞典』昭和11年
• 音楽之友社『新音楽辞典』昭和52年
• 平凡社『音楽大事典』1983年
• 音楽之友社『新編　音楽中辞典』2002年
• 音楽之友社『新訂　標準音楽辞典』2008年

したがって私は「十二平均律」という用語は文脈上でどうしても要求される場面以外では使用すべきではないと考えます。--Kagefumimaru（会話） 2019年7月14日 (日) 07:19 (UTC)

Wikipediaでは事典のみを参考にすべきではないでしょう。Wikipedia:信頼できる情報源を広く参考にすることが望ましいです。事典に限定する理由はありません。--610CH-405（会話） 2019年7月14日 (日) 07:23 (UTC) 一部追記--610CH-405（会話） 2019年7月14日 (日) 07:24 (UTC)

音楽辞典に記載のない音楽用語を一般的なものと考えるのは難しいでしょう。仮に用例があったとしてもそれは特定分野での慣例的用法と考えるべきです。そもそも出典にそれに対応する用語は使用されていません。--Kagefumimaru（会話） 2019年7月14日 (日) 07:33 (UTC)

認識の相違を埋めるのが難しそうなので、私のほうで「前後の文脈から十二平均律と判断できる」と見なし、妥協します。それから、先の妥協案から画像が抜けておりましたね。

長調と短調を表す五度圏

五度圏（ごどけん、英語: circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである (注1)。

五度圏は F♯ / G♭ や D♯ / E♭ といった異名同音関係を利用することで環を形成しており、これは一般に平均律を前提としている (注1)。純正な完全五度に基づくピタゴラス音律では、異名同音はユニゾンやオクターヴ関係にないため閉じた環を形成できない (注1)。例えば、E♭ を起点として完全五度を12回上方向に堆積すると異名同音関係にある D♯ が得られるが (E♭ - B♭ - F - C - G - D - A - E - B - F♯ - C♯ - G♯ - D♯)、この2音は平均律においてユニゾンやオクターヴ関係を有する。しかし、純正な完全五度（周波数比 3:2）に基づくピタゴラス音律による場合、この D♯ と E♭ は正確なユニゾンやオクターヴ関係にならない。すなわち、12の純正な完全五度 (脚注1) と7つのオクターヴ (脚注2) の間には $531441/524288=1.0136432647705078125...$ (脚注3) の差が生じ、この差の大きさをセント値で表すと約23.46セントである。また、この差をピタゴラスコンマと呼ぶ (注2)。一方、平均律の完全五度は純正音程よりも 1/12 ピタゴラスコンマだけ狭められているため、異名同音はユニゾンやオクターヴ関係を有し、一様な完全五度によって閉じた五度圏を形成することができる (注3)。

五度圏はある調から他の調への「遠隔度」を視覚化するのに用いられる (注1)。例えばト長調に対し五度圏上で隣接する5つの調（ホ短調、ニ長調、ロ短調、ハ長調、イ短調）は和声的に近い関係にある近親調である (注4)。一方、五度圏上で最も離れた嬰ハ長調とは和声的に遠い関係にあり、その音階上の三和音に共通するものが1つもない (注5)。

注1：William Drabkin, “Circle of fifths,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 5, pp. 866-867.

注2：Margo Schulter, Pythagorean Tuning and Medieval Polyphony,(http://www.medieval.org/emfaq/harmony/pyth.html ), 1998.

注3：Mark Lindley, “Temperaments,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 25, pp. 248-269.

注4：Ryan J. Thomson, A Folk Musicians Working Guide to Chords, Keys, Scales, and More, Captain Fiddle Publications, 1991, p. 52.

注5：“Circle of fifths,” in The New Oxford Companion to Music, ed. by Denis Arnold, Oxford University Press, 1983, vol. 1, p. 399.

脚注1：周波数比 $\left({\frac {3}{2}}\right)^{12}=129.746337890625$

脚注2：周波数比 $\left({\frac {2}{1}}\right)^{7}=128$

脚注3：${\frac {\left({\frac {3}{2}}\right)^{12}}{\left({\frac {2}{1}}\right)^{7}}}={\frac {531441}{524288}}=1.0136432647705078125...$

--610CH-405（会話） 2019年7月14日 (日) 07:46 (UTC)

脚注を使用するのであればこのようにすることを提案します。なお小数表記したピタゴラスコンマの値は概数ではなく正確な値です。

五度圏（ごどけん、英語：circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである(注1)。

五度圏は F♯/G♭ や D♯/E♭ といった異名同音関係を利用することで環を形成しており、これは一般に平均律を前提としている(注1)。純正な完全五度に基づくピタゴラス音律では異名同音は一致しないため閉じた環を形成できない(注1)。例えばE♭を起点として完全五度を12回上方向に堆積すると異名同音関係にあるD♯が得られる (E♭-B♭-F-C-G-D-A-E-B-F♯-C♯-G♯-D♯)、しかし純正な完全五度 (3:2) による場合、このD♯とE♭は正確なユニゾンやオクターヴ関係にならず、ピタゴラスコンマ（約23.46セント）の差が生じる(注2)（注6）。平均律の完全五度は純正音程よりも1/12ピタゴラスコンマだけ狭められているため、異名同音が一致し、一様な五度によって閉じた五度圏を形成することができる(注3)。

五度圏はある調から他の調への「遠隔度」を視覚化するのに用いられる(注1)。例えばト長調に対し五度圏上で隣接する5つの調（ホ短調、ニ長調、ロ短調、ハ長調、イ短調）は和声的に近い関係にある近親調である（注4）。一方、五度圏上で最も離れた嬰ハ長調とは和声的に遠い関係にあり、その音階上の三和音に共通するものが1つもない（注5）。

注1：William Drabkin, “Circle of fifths,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 5, pp. 866-867. 注2：Margo Schulter, Pythagorean Tuning and Medieval Polyphony,(http://www.medieval.org/emfaq/harmony/pyth.html ), 1998. 注3：Mark Lindley, “Temperaments,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 25, pp. 248-269. 注4：Ryan J. Thomson, A Folk Musicians Working Guide to Chords, Keys, Scales, and More, Captain Fiddle Publications, 1991, p. 52. 注5：“Circle of fifths,” in The New Oxford Companion to Music, ed. by Denis Arnold, Oxford University Press, 1983, vol. 1, p. 399.

注6 :

12の純正な完全5度

$\left({\frac {3}{2}}\right)^{12}=129.746337890625$

は、7オクターヴ

$\left({\frac {2}{1}}\right)^{7}=128$

に対し

${\frac {\left({\frac {3}{2}}\right)^{12}}{\left({\frac {2}{1}}\right)^{7}}}={\frac {531441}{524288}}=1.0136432647705078125$

の差が生じる（約23.46セント）。この差をピタゴラスコンマと呼ぶ。

--Kagefumimaru（会話） 2019年7月14日 (日) 07:56 (UTC)

┌────────────────────────────────────────────────────────────────────────────────────────────────────┘ 返信 ありがとうございます。この方が見やすいですね。では、このご提案をもとに、改めて私の修正案を提示します。

長調と短調を表す五度圏

五度圏（ごどけん、英語: circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである (出典1)。

五度圏は F♯ / G♭ や D♯ / E♭ といった異名同音関係を利用することで環を形成しており、これは一般に平均律を前提としている (注1)。純正な完全五度に基づくピタゴラス音律では、異名同音はユニゾンやオクターヴ関係にないため閉じた環を形成できない (出典1)。例えば、E♭ を起点として完全五度を12回上方向に堆積すると異名同音関係にある D♯ が得られるが (E♭ - B♭ - F - C - G - D - A - E - B - F♯ - C♯ - G♯ - D♯)、純正な完全五度（周波数比 3:2）による場合、この D♯ と E♭ は正確なユニゾンやオクターヴ関係にならず、ピタゴラスコンマ（約23.46セント）の差が生じる (出典2)(脚注1)。平均律の完全五度は純正音程よりも 1/12 ピタゴラスコンマだけ狭められているため、異名同音は正確なユニゾンまたはオクターヴ関係となり、一様な五度によって閉じた五度圏を形成することができる (出典3)。

五度圏はある調から他の調への「遠隔度」を視覚化するのに用いられる (出典1)。例えばト長調に対し五度圏上で隣接する5つの調（ホ短調、ニ長調、ロ短調、ハ長調、イ短調）は和声的に近い関係にある近親調である (出典4)。一方、五度圏上で最も離れた嬰ハ長調とは和声的に遠い関係にあり、その音階上の三和音に共通するものが1つもない (出典5)。

脚注1： 12の純正な完全5度の周波数比

$\left({\frac {3}{2}}\right)^{12}=129.746337890625$

は、7オクターヴの周波数比

$\left({\frac {2}{1}}\right)^{7}=128$

に対し

${\frac {\left({\frac {3}{2}}\right)^{12}}{\left({\frac {2}{1}}\right)^{7}}}={\frac {531441}{524288}}=1.0136432647705078125$

の差が生じる。

出典1：William Drabkin, “Circle of fifths,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 5, pp. 866-867.

出典2：Margo Schulter, Pythagorean Tuning and Medieval Polyphony,(http://www.medieval.org/emfaq/harmony/pyth.html ), 1998.

出典3：Mark Lindley, “Temperaments,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 25, pp. 248-269.

出典4：Ryan J. Thomson, A Folk Musicians Working Guide to Chords, Keys, Scales, and More, Captain Fiddle Publications, 1991, p. 52.

出典5：“Circle of fifths,” in The New Oxford Companion to Music, ed. by Denis Arnold, Oxford University Press, 1983, vol. 1, p. 399.

Kagefumimaruさんの案から変更している点は以下の通りです。

1. スタイル・リンク調整
2. 「注」を「注釈」と「出典」に分割
3. 句読点の修正
4. 「異名同音が一致」という表現をいきなり使うのは読者に不親切なので（理由は前述）、他の表現に差し替え
5. 周波数比であることを示さずにいきなり数値を示すのは不適切なので、「周波数比」という文言を追加

何なりとコメントください。--610CH-405（会話） 2019年7月14日 (日) 08:20 (UTC) 脚注内の改行を調整--610CH-405（会話） 2019年7月14日 (日) 08:21 (UTC)

まず「異名同音が一致しない」は典拠では "since this system does not admit enharmonic equivalents" という箇所です。これは直訳すれば「このシステムは異名同音の同一視を許容しないため」となりますが、これは「異名同音が一致しない」で十分に伝わるでしょう。「ユニゾンやオクターヴ関係にないため」というのではなぜそれで「閉じた環を形成できない」のかよくわかりませんし、そもそも典拠にそのような表現はありません。ここでは"equivalent"という概念の提示は不可欠です。--Kagefumimaru（会話） 2019年7月14日 (日) 08:36 (UTC)

「異名同音が一致する」という表現は「一致しないケースがある（本来は一致しない）」ことが前提でありますが、いきなり一致すると言われても専門的な知識のない利用者には何のことだかわからないので、ある程度具体性のある表現を用いるべきです。前述のように「異名同音は異なるピッチクラスを持つ。」とリンクで飛ばす方式がダメであるなら、何か別の案をお示し願います。--610CH-405（会話） 2019年7月14日 (日) 08:44 (UTC)

私の文案ではまず「異名同音が一致しない」が登場し「異名同音が一致する」はその後です。--Kagefumimaru（会話） 2019年7月14日 (日) 08:50 (UTC)

そうじゃなくて、「異名同音が本来一致しない」という知識がないと、「異名同音が一致しない」だろうが「異名同音が一致する」だろうが何のこっちゃです。これは、一致するとは何なのかを明示することにより解決できます。--610CH-405（会話） 2019年7月14日 (日) 08:53 (UTC)

私の文案で「異名同音が本来一致しない」という知識は事前にまったく必要ありません。まず異名同音が何であるかについては「F♯/G♭ や D♯/E♭ といった異名同音関係」という記述で説明しています。「F♯/G♭」というのはF♯とG♭を同一視するという意味です。典拠ではこの様になっています "Such an arrangement is dependent on an Enharmonic relationship somewhere in the circle; this is usually reckoned at F/G for the major keys and at D/E for the minor keys. "そして次に異名同音を同一視できないケースについて説明しています、なにか不足がありますか。--Kagefumimaru（会話） 2019年7月14日 (日) 09:02 (UTC)

「一致」の意味が不明確であることです。そもそも、「一致」という言葉遣いも飽くまであなたの意訳でしょう。貴方が仰るように出典で「異名同音を同一視できないケース」となっているのであれば、「異名同音が一致する / しない」ではなく、「異名同音を同一視できる / できない」のままでいいではありませんか。それに、直訳のままのほうが明確です。わざわざ曖昧な表現にする必要はありません。--610CH-405（会話） 2019年7月14日 (日) 09:08 (UTC)

「同一視する」も私の意訳が入っています、"enharmonic equivalents"は文字通りには「エンハーモニック等価」であり、むしろ「一致」のほうが近いのですが、ここでは"enharmonic"と異名同音という訳語の困難な関係を考慮する必要があります。--Kagefumimaru（会話） 2019年7月14日 (日) 09:18 (UTC)

すみません、専門用語の英語での言い方にあまり詳しくないもので……。うーむ、難しいですね。そもそも「異名同音」は「平均律において異なる音名だが同一のピッチクラスの音」を指すので、シンプルに「異名同音が成立しない」とするのが意味的には妥当な線ではあるかと。--610CH-405（会話） 2019年7月14日 (日) 09:25 (UTC)

案を提示します「五度圏は F♯とG♭ や D♯とE♭ といった音を同一とする異名同音関係を利用することで環を形成しているが、これは一般に平均律を前提としている。純正な完全五度に基づくピタゴラス音律では異名同音は一致しないため閉じた環を形成できない。--Kagefumimaru（会話） 2019年7月14日 (日) 09:31 (UTC)

「異名同音が成立しない」というのは誤りです、それは日本語の字面に引きづられてエンハーモニック概念を誤解しています。それでは12回の5度の連鎖で異名同音に至ることが説明できなくなります。--Kagefumimaru（会話） 2019年7月14日 (日) 09:34 (UTC)

┌────────────────────────────────────────────────────────────────────────────────────────────────────┘ その案だと、意図があまり伝わらないように思います（"/" を日本語で置き換えただけなので）。元々のKagefumimaruさんの案で、「一致」→「成立」と置き換えるだけで良いと思いますよ。「誤解」→具体的にご説明ください。もしくは、別の文案の提示をお願いします。--610CH-405（会話） 2019年7月14日 (日) 09:38 (UTC)

エンハーモニックは「同じ音」ではなく「同じような音」です。もし「異名同音が成立しない」としたら次の「E♭を起点として完全五度を12回上方向に堆積すると異名同音関係にあるD♯が得られる」という説明も成立しません。--Kagefumimaru（会話） 2019年7月14日 (日) 09:44 (UTC)

なるほど、ありがとうございます。それでは、「E♭を起点として完全五度を12回上方向に堆積すると平均律において異名同音関係にあるD♯が得られる」というのはどうでしょうか？ そもそもピタゴラス音律で「異名同音」と言っていること自体が不適切、もしくは誤解を与える表現ではありますので。--610CH-405（会話） 2019年7月14日 (日) 09:48 (UTC)

エンハーモニック関係はピタゴラス音律でも成立します。すでに述べましたがあなたは「異名同音」を字面で理解しているために誤解しています。とりあえず私の文案の「異名同音」を全部「エンハーモニック」に置き換えてみてください。--Kagefumimaru（会話） 2019年7月14日 (日) 09:57 (UTC)

「誤解されやすい」異名同音を避けた案です。

五度圏（ごどけん、英語：circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである(注1)。

五度圏は F♯/G♭ や D♯/E♭ といった異名同音関係を利用することで環を形成しており、これは一般に平均律を前提としている(注1)。純正な完全五度に基づくピタゴラス音律では異名同音を利用して閉じた環を形成することはできない(注1)。例えばE♭を起点として完全五度を12回上方向に堆積すると異名同音関係にあるD♯が得られる (E♭-B♭-F-C-G-D-A-E-B-F♯-C♯-G♯-D♯)、しかし純正な完全五度 (3:2) による場合、このD♯とE♭は正確なユニゾンやオクターヴ関係にならず、ピタゴラスコンマ（約23.46セント）の差が生じる(注2)（注6）。平均律の完全五度は純正音程よりも1/12ピタゴラスコンマだけ狭められているため、異名同音によって閉じた五度圏を形成することができる(注3)。

--Kagefumimaru（会話） 2019年7月14日 (日) 10:05 (UTC)

良いですね。これであれば誤解が生じにくく、説明としてもさらに分かりやすいと思います。--610CH-405（会話） 2019年7月14日 (日) 10:08 (UTC)

若干修正です

五度圏（ごどけん、英語：circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである(注1)。

五度圏は F♯/G♭ や D♯/E♭ といった異名同音関係を利用することで環を形成しており、これは一般に平均律を前提としている(注1)。純正な完全五度に基づくピタゴラス音律では異名同音を利用して閉じた環を形成することはできない(注1)。例えばE♭を起点として完全五度を12回上方向に堆積すると異名同音関係にあるD♯が得られる (E♭-B♭-F-C-G-D-A-E-B-F♯-C♯-G♯-D♯)、しかし純正な完全五度 (3:2) による場合、このD♯とE♭は正確なユニゾンやオクターヴ関係にならず、ピタゴラスコンマ（約23.46セント）の差が生じる(注2)（注6）。平均律の完全五度は純正音程よりも1/12ピタゴラスコンマだけ狭められているため、このD♯とE♭が一致し、それによって閉じた五度圏を形成することができる(注3)。

--Kagefumimaru（会話） 2019年7月14日 (日) 10:13 (UTC)

賛成 これで、私の2019年7月14日 (日) 08:20 (UTC) のコメントにある 4. の問題は解決としてよいと思います。--610CH-405（会話） 2019年7月14日 (日) 10:15 (UTC)

全体の文案です。私はこれで異論ありません。

五度圏（ごどけん、英語：circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである(注1)。

五度圏は F♯/G♭ や D♯/E♭ といった異名同音関係を利用することで環を形成しており、これは一般に平均律を前提としている(注1)。純正な完全五度に基づくピタゴラス音律では異名同音を利用して閉じた環を形成することはできない(注1)。例えばE♭を起点として完全五度を12回上方向に堆積すると異名同音関係にあるD♯が得られる (E♭-B♭-F-C-G-D-A-E-B-F♯-C♯-G♯-D♯)、しかし純正な完全五度 (周波数比 3:2) による場合、このD♯とE♭は正確なユニゾンやオクターヴ関係にならず、ピタゴラスコンマ（約23.46セント）の差が生じる(注2)（注6）。平均律では完全五度が純正音程よりも1/12ピタゴラスコンマだけ狭められているため、D♯とE♭が一致し、閉じた五度圏を形成することができる(注3)。

五度圏はある調から他の調への「遠隔度」を視覚化するのに用いられる (出典1)。例えばト長調に対し五度圏上で隣接する5つの調（ホ短調、ニ長調、ロ短調、ハ長調、イ短調）は和声的に近い関係にある近親調である (出典4)。一方、五度圏上で最も離れた嬰ハ長調とは和声的に遠い関係にあり、その音階上の三和音に共通するものが1つもない (出典5)。

脚注1： 12の純正な完全5度の周波数比

$\left({\frac {3}{2}}\right)^{12}=129.746337890625$

は、7オクターヴの周波数比

$\left({\frac {2}{1}}\right)^{7}=128$

に対し

${\frac {\left({\frac {3}{2}}\right)^{12}}{\left({\frac {2}{1}}\right)^{7}}}={\frac {531441}{524288}}=1.0136432647705078125$

の差が生じる。

出典1：William Drabkin, “Circle of fifths,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 5, pp. 866-867.

出典2：Margo Schulter, Pythagorean Tuning and Medieval Polyphony,(http://www.medieval.org/emfaq/harmony/pyth.html ), 1998.

出典3：Mark Lindley, “Temperaments,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 25, pp. 248-269.

出典4：Ryan J. Thomson, A Folk Musicians Working Guide to Chords, Keys, Scales, and More, Captain Fiddle Publications, 1991, p. 52.

出典5：“Circle of fifths,” in The New Oxford Companion to Music, ed. by Denis Arnold, Oxford University Press, 1983, vol. 1, p. 399.

--Kagefumimaru（会話） 2019年7月14日 (日) 10:28 (UTC)（若干修正--Kagefumimaru（会話） 2019年7月14日 (日) 10:31 (UTC)）

賛成 この内容で異論ありません。前半部分のリンク先（リダイレクト回避・曖昧さ回避）やマークアップ、スペースの入れ方やハイフンの種類を修正した上で、以下に修正したものを改めて示します。文章は「得られる (E♭-B♭-F-C-G-D-A-E-B-F♯-C♯-G♯-D♯)、しかし」の部分だけおかしかったので直しましたが、他は全く変えていません。

長調と短調を表す五度圏

五度圏（ごどけん、英語: circle of fifths）は、12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである (出典1)。

五度圏は F♯ / G♭ や D♯ / E♭ といった異名同音関係を利用することで環を形成しており、これは一般に平均律を前提としている (出典1)。純正な完全五度に基づくピタゴラス音律では異名同音を利用して閉じた環を形成することはできない (出典1)。例えば E♭ を起点として完全五度を12回上方向に堆積すると異名同音関係にある D♯ が得られるが (E♭ - B♭ - F - C - G - D - A - E - B - F♯ - C♯ - G♯ - D♯)、純正な完全五度（周波数比 3:2）による場合、この D♯ と E♭ は正確なユニゾンやオクターヴ関係にならず、ピタゴラスコンマ（約23.46セント）の差が生じる (出典2)(脚注1)。平均律では完全五度が純正音程よりも1/12ピタゴラスコンマだけ狭められているため、D♯ と E♭ が一致し、閉じた五度圏を形成することができる (出典3)。

五度圏はある調から他の調への「遠隔度」を視覚化するのに用いられる (出典1)。例えばト長調に対し五度圏上で隣接する5つの調（ホ短調、ニ長調、ロ短調、ハ長調、イ短調）は和声的に近い関係にある近親調である (出典4)。一方、五度圏上で最も離れた嬰ハ長調とは和声的に遠い関係にあり、その音階上の三和音に共通するものが1つもない (出典5)。

脚注1： 12の純正な完全5度の周波数比

$\left({\frac {3}{2}}\right)^{12}=129.746337890625$

は、7オクターヴの周波数比

$\left({\frac {2}{1}}\right)^{7}=128$

に対し

${\frac {\left({\frac {3}{2}}\right)^{12}}{\left({\frac {2}{1}}\right)^{7}}}={\frac {531441}{524288}}=1.0136432647705078125$

の差が生じる。

出典1：William Drabkin, “Circle of fifths,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 5, pp. 866-867.

出典2：Margo Schulter, Pythagorean Tuning and Medieval Polyphony,(http://www.medieval.org/emfaq/harmony/pyth.html ), 1998.

出典3：Mark Lindley, “Temperaments,” in The New Grove Dictionary of Music and Musicians, 2nd ed., ed. by Stanley Sadie (London: Macmillan, 2001), vol. 25, pp. 248-269.

出典4：Ryan J. Thomson, A Folk Musicians Working Guide to Chords, Keys, Scales, and More, Captain Fiddle Publications, 1991, p. 52.

出典5：“Circle of fifths,” in The New Oxford Companion to Music, ed. by Denis Arnold, Oxford University Press, 1983, vol. 1, p. 399.

これでいかがでしょうか。ちなみに、{{Efn}}を使えば出典と注釈を分離できますので、記事反映の際はよろしくお願いします。--610CH-405（会話） 2019年7月14日 (日) 10:45 (UTC)

賛成 異論ありません。--Kagefumimaru（会話） 2019年7月14日 (日) 10:48 (UTC)

Gruppettoさんの意見を伺ったうえで、賛成いただければ記事に反映という形でどうでしょう？ --610CH-405（会話） 2019年7月14日 (日) 11:04 (UTC)

五度圏の図についてですが、当初は日本語版なのだから当然日本語の図であるべき、と考えていましたが、日本語の図は音部記号が書かれていないという問題があることに気付きました（まあ、調号の位置から推測はできますが）。また、現実には多数派であるポピュラー音楽の関係者は英語の調名を使うのが普通ですし、クラシック関係者もドイツ語名を使いますから、日本語の調名は現場ではあまり使われていないでしょう。そういう意味では英語版の図でも良いかなと思います。最後に示された案に賛成します。Gruppetto（会話） 2019年7月14日 (日) 11:32 (UTC)

合意成立により最終案によって記事を編集し、コメント依頼は取り下げました。--Kagefumimaru（会話） 2019年7月14日 (日) 12:31 (UTC)

• ありがとうございます Kagefumimaruさん、記事への反映および各種終了手続きありがとうございました。議論に参加下さった各位にも感謝申し上げます。なお、関係する各議論の上部に{{解決済み}}を貼付しました。--610CH-405（会話） 2019年7月14日 (日) 12:40 (UTC)
• コメント 参加者の皆さま、お疲れ様でした。解決できたようで、よかったです。強いて言えば、Wikipedia:信頼できる情報源#日本語以外の言語で書かれた情報源あたりがクリアできていないのが難点かもしれません。そのほか、問題など生じたら、後で解決すればよいかと思います。また、せっかく英語版から翻訳されたものがこのページに残っているのですから、「定義」以外のところも、Wikipedia:信頼できる情報源のついている部分は移植したほうが、読者の皆さんの理解の役に立つのではないかと思います。それと、歴史のところなんですけど、音楽事典のたぐいをみるとハイニヒェンが最初となっているものが多いみたいなんですが、原典の出版年を比較するとディレツキーの方が早いみたいですね。ハイニヒェンが最初とする主張にも理由があるのかもしれませんが、そのあたりはもう少しスペシフィックな論文などを調べてみないとわからないかもしれません。--Takabeg（会話） 2019年7月14日 (日) 12:55 (UTC)

Gruppettoさんのrevertに関して

Gruppettoさんが私の編集をrevertしたようですが、revertの理由を教えてください。

ノートでの議論が原因かと思い、簡単に読んでみましたが、ピタゴラスコンマの話がメインのようなので全文revertした理由にならないような。--ざつもくりん（会話） 2023年9月27日 (水) 07:59 (UTC)

まず、利用者:ざつもくりんさんが加筆する前の版では、冒頭は「12の長調あるいは短調の主音を完全五度上昇あるいは下降する様に並べて閉じた環にしたものである」というニューグローヴ世界音楽大事典に基づいた適切な定義文が書かれていました。ざつもくりんさんはこれを壊し、音楽家が普通に用いている「完全五度」という言葉を、「半音7つ分」などという通常音楽家は用いない奇妙な表現に置き換えました。「12の長調あるいは短調の主音」も「音名」に置き換えられました。不適切の極みです。百科事典の記事としては質の劣化でしかありません。その後に続く「五度圏は下記の用途に用いる事ができる」も全くの独自研究です。それ以下の部分も「五度圏」の説明として的を射ない独自研究を含んだ的外れな説明が続いています。極めて不適切な書き換えが行われているので、以前の版に戻させていただきました。また、ざつもくりんさんは小方厚『音律と音階の科学　新装版　ドレミ…はどのように生まれたか』を参考にしているようですが、そもそも小方厚氏は物理畑の人間であり音楽学者ではなく音楽の専門家でもありません。音程におけるざつもくりんさんの加筆も酷いもので、間違いや不適切な表現が多く、直すのに苦労しました。こちらの記事ではもはや修正は難しい状況となっていったため、前の版に戻すしかありませんでした。ざつもくりんさんは楽典や音楽理論を正規に学んだことはあるのでしょうか？--Gruppetto（会話） 2023年9月27日 (水) 15:01 (UTC)

出典付きで書いたものを「独自研究」とまでいうからには、より素晴らしい出典が出せるものと思います。 まずは出典を出していただけないでしょうか。--ざつもくりん（会話） 2023年9月28日 (木) 12:22 (UTC)

ざつもくりんさんが加筆する前の版＝現在の版には、十分に出典が示されています。--Gruppetto（会話） 2023年9月28日 (木) 13:48 (UTC)

ん？それは私の記述を削る理由にはならないような。私の記述（の元になっている小方氏の本の記述）が「独自研究」だとする証拠の文献を出していただけますか？--ざつもくりん（会話） 2023年9月28日 (木) 13:56 (UTC)

追記： >小方厚氏は物理畑の人間であり音楽学者ではなく音楽の専門家でもありません。 >楽典や音楽理論を正規に学んだことはあるのでしょうか？

小方厚氏の記述が「専門家ではない」から信用ならないというからには、当然専門家の本を出典として提出して小方氏の記述のどこが間違っているかを説明してください。--ざつもくりん（会話） 2023年9月28日 (木) 14:04 (UTC)

Wikipedia:BURDENをお読み下さい。出典を示す責任は掲載を希望する側にあります。Gruppetto（会話） 2023年9月28日 (木) 14:10 (UTC)

そうですよ。だから私は出典を出したわけです。ところがそれは「独自研究」だとおっしゃるので証拠を出してください、といってるわけです。 それとも「独自研究」との主張を取り消すのでしょうか。--ざつもくりん（会話） 2023年9月28日 (木) 14:14 (UTC)

あなたの版は文章の長さの割に出典が少なすぎます。冒頭部にも2番目の節にも出典が示されていません。あなたが新たに出した出典は「音律と音階の科学 pp.40-41,49,51.」と、「音律と音階の科学 p.72.」の二つしかありません。これでは独自研究でないことを証明するには不十分です。Gruppetto（会話） 2023年9月28日 (木) 14:24 (UTC)

それじゃ1行目の出典： >the circle of fifths (Fig. 2.7) is a group of 12 members, generated by ρ^7;

Keiji Hirata, Satoshi Tojo,Masatoshi Hamanaka Music, Mathematics and Language The New Horizon of Computational Musicology Opened by Information Science p48.

ρは半音一つ分なので、ρ^7は半音7つ分。

こういっては申し訳ないですが、「独自研究だ！」と主張している割にどこが独自研究なのか明言していない状態で、さすがにそれは議論としてちょっと…と思ってしまうので、どこが独自研究で、どこがどう間違っていて、正しくはどうなのかを具体的に教えていただけますか？

--ざつもくりん（会話） 2023年9月28日 (木) 14:32 (UTC)

横から失礼 ざつもくりんさんの編集内容を私は精査しておりませんので突っ込んでのコメントはこの時点で差し控えますけれど、Gruppettoさんは 2023年9月27日 (水) 15:01 (UTC) のコメントでこの箇所が独自研究だ、と挙げていらっしゃるではありませんか。(これが独自研究箇所の全例なのか一例なのかは分かりませんけれど)

相手に向かって「議論としてちょっと…」とおっしゃるのであれば、まずはざつもくりんさんがGruppettoさんのコメントをきちんとお読みになってはいかがでしょうか。--610CH-405（会話） 2023年9月28日 (木) 16:13 (UTC)

ざつもくりんさんへの 返信 元々ニューグローヴに基づいた適切な冒頭文があるのに、ざつもくりんさんの版のようにわざわざ完全五度を「半音7つ分」と書く必然性がありません。「完全五度（半音7つ分）」と書くならまだ良いですが。それから

「五度圏は下記の用途に用いる事ができる：

完全5度、完全4度の音を調べる　

音階の構成音や調号を調べる　

近親調を調べる」

↑こんなことを書く必要もありません。百科事典の記事として「五度圏」について説明するべきで、本質から外れています。「完全5度、完全4度の音を調べる」「音階の構成音や調号を調べる」のにわざわざ五度圏の図を持ち出す必要もない。そんなことは楽典の基礎であって本末転倒です。

その後の「完全5度と完全4度」という節も無意味です。

　「五度圏では隣り合う2音は半音7つ分離れている為、五度圏上の外側にある大文字で書かれた音（例：C）と右隣りの音（例：G）を右隣りのもののほうが高い音（で1オクターブ以内にあるもの）になるよう譜面上に並べると、その2音は完全5度の関係になる」

ってそもそも最初から「五度圏」という名前なのに「半音7つ分離れている為」「その2音は完全5度の関係になる」って、原因と結果が逆でしょう。「五度圏では隣り合う2音は完全五度離れている」とストレートに書けば良い。しかしそんなことは冒頭文にすでに書かれているのですから、この説の存在は無意味です。

次の「五度圏の成り立ち」の節ですが、これも問題です。最初の五度圏の図はバロック音楽時代の1677年に登場しますが、あなたの版ではあたかもピタゴラスに由来するかのように読者に誤解を与えるでしょう。ピタゴラス音律と五度圏の関係について極めて適当で曖昧な内容です。

次の「音階」という節、これは独自研究そのものでしょう。いや、書いている内容は別に間違ってませんけど、「五度圏を利用すると長音階の音階構成音を調べられる」って、音階の構成音を知るのにいちいち五度圏の表を持ち出して主音の左側一つと右側五つで調べるんですか？馬鹿げている。そんなんじゃ何の楽器も弾けませんよ。結果的にそうなる、という話でしょう。要するにこれも原因と結果がひっくり返っているんですよ。例えば次に弾く曲が変ホ長調だから、変ホ長調の構成音を五度圏の表で調べる音楽家などいませんよ。五度圏の図は音や調の近親関係を視覚的に示した物であって、あなたが書いているのは実際の演奏・作曲とは本質的に関係の薄いトリビアのようなものです。百科事典として「五度圏」を説明することから外れています。Gruppetto（会話） 2023年9月28日 (木) 16:21 (UTC)

ご説明ありがとうございます。これなら理解です。 「全消しされるほどの独自研究はしてないよな」と思っていたので議論させていただきましたが、前半は旧バージョンのほうが正確、後半は間違ってないが特筆性が薄い、という事ですね。 旧バージョンにする事に合意です。お手数をおかけいたしました。ありがとうございます--ざつもくりん（会話） 2023年9月28日 (木) 16:45 (UTC)