セント (音楽)

モノコードによる1セントと半音の比較

線型の周波数尺度 (Hz) ではオクターヴは指数関数的である

対数的な尺度 (セント) ではオクターヴは等間隔になる

セント (cent) は音程を測定するための対数単位である。12平均律はオクターヴをそれぞれ100セントの12の半音に分割する。一般的にセントは微小な音程を測定するため、あるいは音律による音程の大きさを比較するために用いられる。実際1セントの音程は小さすぎて聴き分けることは難しい。

アレクサンダー・ジョン・エリスは、ロバート・ホルフォード・マクダウォル・ボーザンケットの提案により、ガスパール・ド・プロニーが1830年代に開発した音響対数値の小数半音システムに基づいてこの測定法を作り上げた。エリスは世界中の楽器を広く測定するにあたり、セント値を用いて報告し、その音階を比較した。そしてヘルマン・フォン・ヘルムホルツの『音感覚論』のエリスによる英訳版でさらなる記述とシステムの採用が行われた。このシステムは音高や音程を比較的正確に示し比較するための標準的な方法となった。

使用

平均律（黒）とピタゴラス音律（緑）の音程の比較

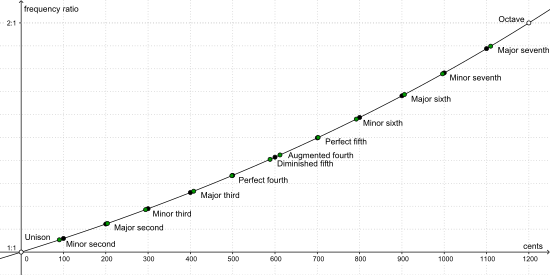
デシベルが強度に関してそうであるように、セントは2つの周波数の比である。平均律の半音の間隔は100セントと定義される。オクターヴ（2つの音の周波数比が2:1）は12半音であり、1200セントである。したがって1200セントごとに周波数は2倍になるので、1セントの周波数比は 2^1/1200 に等しい。この値は約 1.0005777895 である。

2つの音 a と b との周波数が知られている場合、a と b との間隔のセント値は次式で算出できる。

$n=1200\cdot \log _{2}\left({\frac {b}{a}}\right)\approx 3986\cdot \log _{10}\left({\frac {b}{a}}\right)$

同様に a と b との間隔のセント値 n が知られている場合、b は次式で算出できる。

$b=a\times 2^{n/1200}$

異なる音律を比較するために、諸々の音程の大きさをセントに変換することが行われる。例として純正律の長三度は周波数比で5:4と示される。これは上の式によって約386セントである。平均律で調律されたピアノの長三度は400セントとなる。この14セントの差は半音の約7分の1であり、容易に聴き取れる。

参考文献

• Ellis, Alexander J.; Alfred J. Hipkins (1884), “Tonometrical Observations on Some Existing Non-Harmonic Musical Scales”, Proceedings of the Royal Society of London 37 (232–234): 368–385, doi:10.1098/rspl.1884.0041, JSTOR 114325, https://jstor.org/stable/114325.