球充填

球充填(きゅうじゅうてん、英語: sphere packing)とは、互いに重なり合わない球を並べて空間を充填することである。通常は同一の大きさの球と3次元ユークリッド空間を扱う。しかし、球の大きさが一様ではない場合や、2次元空間(その場合の球は円)や高次元空間(その場合の球は超球)、さらには双曲空間のような非ユークリッド空間にも適用できる (位相幾何的に定式化される)。
典型的な球充填問題とは、ある空間について最も稠密に球を詰め込む配置を見出す問題である。空間全体に対する球によって占められた空間の比率を充填密度(英: density of arrangement)と呼ぶ。無限に広い空間への充填では、測定する体積によって局所的な充填密度が変わるため、通常は密度の平均を最大化するか、十分大きな体積を測定するときの漸近的な密度を最大化することを問題とする。
3次元空間の充填では、等しい大きさの球による最密充填は空間の74%を占める。等しい大きさの球によるランダム充填は一般に64%前後の密度を持ち、最も緩い充填は5.5%ぐらいになることが実験によって確かめられている。
球充填の分類[編集]
球面の中心が格子と呼ばれる極めて対称的なパターンとなる配置を、正規 (regular) 配置(または周期 (periodic) 配置、あるいは格子 (lattice) 配置と呼ぶ。格子状に配置されていない場合は、非正規 (irregular) 配置または非周期 (aperiodic) 配置と呼ぶ。正規配置は非正規配置よりも扱いやすく、対称性の高さのおかげで分類や密度測定が容易に行える。
円充填[編集]

3次元における球充填問題は、任意次元における球充填という問題のクラスの一部である。2次元における同等な問題は円による平面充填である。
2次元ユークリッド空間(平面)については、カール・フリードリヒ・ガウスが最も密度の高い円の正規配置は六方充填配置であることを証明した。これは、円の中心が六方格子(ハニカム構造のようなもの)になっており、それぞれの円は6個の円で囲まれている。その充填密度は
である。
1940年、ハンガリー(マジャル人)の数学者ラースロー・フェイェシュ=トートは、六方格子が正規も非正規も含めたあらゆる円充填の中で最も高密度であることを証明した。
これを一般化した概念を「円充填 (circle packing)」と呼び、様々な大きさの円を組み合わせて平面を充填することを指す。これは、等角写像、リーマン面といった概念の離散化した類似物を生み出す。
正規充填[編集]
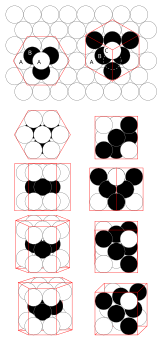


最密充填[編集]
3次元ユークリッド空間において、等しい球のもっとも稠密な配置は最密構造と呼ばれる構造の族を成す。そのうちの一つを構築する方法の例を以下に示す。まず平面上で球を稠密に配置する。3つの球が互いに接するよう配置すると、その真ん中にできた凹みに第4の球を置くことができる。これを一段目の上のあらゆる箇所で行えば、新たな稠密な配置が生成される。第3層は、上から見て第1層と同じ配置になる場合と、第1層の凹みのうち第2層が使っていない位置に球を配置する場合がある。つまり一つの層が取り得る配置は3種類存在する。これらをA、B、Cと名付ける。
このような最密構造の族の中には、正規格子となる単純な配置が二つ存在する。その一方は層がABCABC…という順で並ぶもので、立方最密充填(または面心立方充填)と呼ばれる。もう一方はABAB…と交互に並ぶもので、六方最密充填と呼ぶ。しかし、これら以外にも任意の層の組合せが可能である(ABAC、ABCBA、ABCBAC、など)。いずれの配置も1つの球は12個の球に囲まれており、平均密度は
- (A093825)
である。
ガウスは1831年にこれらの配置が正規配置の中で最も高密度であることを証明した[1]。
1611年、ヨハネス・ケプラーは、これが正規配置と非正規配置全てについて最高密度の配置であると予想した。この命題はケプラー予想と呼ばれる。1998年、トーマス・C・ヘイルズは1953年にフェイェシュ=トートが示唆した手法を使って、ケプラー予想を証明したと発表した。ヘイルズの証明は、コンピュータを使ってあらゆる個々のケースを調べつくすという方法であった。審査員はヘイルズの証明の正しさを99%としており、ケプラー予想は「ほぼ」証明された状態と言える。後の2014 年、Halesの率いるチームは自動証明検証ツールを用いて形式的証明を完了したと発表し、疑念を晴らした。[2]。
その他の一般的な格子充填[編集]
物理系ではほかの種類の格子充填もよくみられる。例として、 の密度を持つ立方格子や、 の密度を持つ六方格子、 の密度を持つ正方格子がある。またもっとも疎な格子充填では密度は0.0555である[3]。
密度の低いジャミング充填[編集]
球充填において、隣接する球同士が押さえつけあって互いを拘束している状態をジャミングという。ジャミングしている球充填で最も疎なものは、密度が0.49365しかない希薄な面心立方格子である[4]。
非正規充填[編集]
球を稠密に配置しようとすると、3個の球を互いに接するように配置して、4つ目をその凹みに配置することになる。このようにして作られる配置は、5個目の球までは上述した正規配置のいずれかと一致する。しかし、6個目の球を配置するといかなる正規配置とも一致しなくなる。さらにこの手順を続けることで、圧縮に対して安定なランダム稠密配置を構築できる可能性がある[5]。
球を1つずつ無作為に追加していって圧縮すると、一般にそれ以上圧縮できない「非正規」充填もしくは「ジャミング」充填配置に行きつく。非正規充填の充填密度は約64%となる。2008年の研究では、63.4%が密度の上限であることが解析的に予想されている[6]。1次元や2次元では事情が異なり、1次元球(線分)または2次元球(円盤)を圧縮すると正規充填が生じる。
超球充填[編集]
3次元より高次元では、8次元までの超球の最密正規充填が知られている[7]。超球の非正規充填についてはほとんど何も知られていない。次元によっては最密充填が非正規であるかもしれず、いくつかの次元(例えば10次元)では既知の最も密な非正規充填の方が既知の最も密な正規充填よりも密度が高い[8]。
この問題は20世紀中ごろから関心をもたれ始め、4次元の場合については1982年にエリッヒ・フリードマンによって正24胞体の頂点を中心とする配置が最密になることが証明されている。[9]

2016年、マリナ・ヴィヤゾフスカは8次元空間において正規・非正規を問わない最適充填がE8格子だと証明した。さらにその直後、共同研究者とともに、24次元における最適充填がリーチ格子だという証明を発表した。どちらの格子もその次元における既知の配置の中でもっとも稠密なものであった[10]。ヴィヤゾフスカの証明では、慎重に選ばれたモジュラー関数のラプラス変換を用いて球対称な関数 を構築する。 はそれ自身およびフーリエ変換 がどちらも原点で1となるように構築される。さらに、充填の中央にある球の外では が負となる一方、は常に正となるようにすることで、原点以外のすべての格子点で および がゼロになることを示せる。その上で に関するポアソン和公式を用い、想定される最適格子の密度をほかのあらゆる格子の密度と比較する[11]。査読論文の中ではないが、ピーター・サルナックはこの証明を「驚くほど簡潔」と評し、「論文の冒頭を読むだけで証明が正しいと分かるだろう」と述べた[12]。[訳語疑問点]
高次元に関する別のアプローチとして、最密充填の密度の下界を漸近的に求めようとする研究がある。現在までに得られた最大の成果は、n 次元ではある数 c について cn2−n 以上の密度を持つ格子が存在するというものである[13]。
多種球充填[編集]


球充填と関連する化学や物理の問題には、球サイズが一つと見なせないものが多い。異なる種類の球で稠密充填を作るには、サイズごとに別の領域に分かれてそれぞれ最密充填を作るか、あるいは異なる種類の球が混合して侵入型化合物のような配置を取るかの選択肢がある。球のサイズの種類が増えると(あるいは連続分布すると)問題は急速に扱いづらくなるが、二通りのサイズの剛球に関する研究はいくつか存在する。
二種類の球のサイズに開きがある場合には、大球が最密充填配置を取った上で、小球が格子間の空隙(八面体型もしくは四面体型)に収まることができる。このような侵入型充填の密度は半径比に強く依存するが、半径比が小さい極限では大球の充填密度を下げずに小球が空隙に侵入することができる[15]。大球が最密配置ではない場合も含め、半径比0.29099以下の小球ならばいかなる配置にも侵入可能である[16]。
小球の半径が大球の0.41421倍を超えると、最密構造の八面体格子間位置にさえ収まることができなくなる。このときホスト格子は膨張して空隙を広げるか(全体の密度は低下する)、より複雑な結晶化合物構造へと再配置するかの選択を迫られる。半径比0.659786以下では最密構造よりも充填率の高い配置が知られている[14][17]。
また、二種球充填において可能な充填密度の上界も得られている[18]。
化学の分野では、イオン結晶をはじめとして、成分イオンの電荷のため化学量論を保たなければならない状況が多く、これが充填問題に対する拘束条件となる。さらに、電荷間の静電相互作用のエネルギーを最小化する必要もある。これらの影響で最適な充填は多種多様なものになる。
双曲空間[編集]
円や球の概念は双曲空間にも拡張可能だが、最密充填を探すのはユークリッド空間よりはるかに難しい。双曲空間では1つの球を取り囲む球の個数には制限がない(たとえば、フォードの円は、同等な双曲円がそれぞれ互いに無限個の円と接しているような配置と考えられる)し、平均密度の概念も正確に定義することすら難しい。いかなる双曲空間においても、最密充填はほぼ常に非正規充填である[19]。
このような困難にもかかわらず、K. Böröczkyは n ≥ 2 である n 次元双曲空間における球充填の密度の普遍的な上界を得た[20]。3次元において Böröczky の上界はおよそ85.327613%で、 シュレーフリ記号 {3,3,6} で表されるホロ球面充填(en:order-6 tetrahedral honeycomb)がこの値を取る[21]。3次元双曲空間の密度の上界を与えるホロ球面充填はこれ以外に少なくとも3つ知られている[22]。[訳語疑問点]
互いに接する球の組[編集]
単位球による任意の有限充填についての接触グラフとは、ノードが球を表し、二つのノードがエッジで結ばれていれば二球が互いに接していることを表すようなグラフである。接触グラフに含まれるエッジの集合の濃度は互いに接する球の二つ組の数を与える。同様に3閉路の数は三つ組の数を、四面体の数は四つ組の数を与える(一般に、n 次元の球充填と関連付けられる接触グラフについて、グラフに含まれる n 単体集合の濃度は、球充填に含まれる互いに接する (n + 1) 組の数を表す)。3次元ユークリッド空間における、互いに接する二つ組、三つ組、四つ組それぞれの数に対する非自明な上界がカルガリー大学のKároly BezdekとSamuel Reidによって発見された[23]。
その他の空間[編集]
超立方体の角を球で充填する問題は、誤り検出訂正符号の設計に対応している(この場合の球はハミング距離で定義される)。充填する球の半径が d であるとき、それらの中心は 2t + 1-誤り訂正符号の符号語となる。格子充填は線型符号に対応する。これ以外にもユークリッド空間の球充填は誤り訂正符号といくぶん関連性がある。例えば、2元ゴレイ符号は24次元のリーチ格子と密接に関連している。詳しくはConway J.H., Sloane N.J.H. (1998) [24]を参照のこと。
ポップカルチャーでの言及[編集]
カート・ヴォネガットの小説『猫のゆりかご』には、アイス・ナインという物質が登場する。その特性の説明として球の様々な充填方法があることが説明される。アイス・ナインは架空の水分子であり、それに触れた他の水分子をアイス・ナインの状態に変化させる性質がある。
関連項目[編集]
脚注[編集]
- ^ C.F. Gauss (1831). “Besprechung des Buchs von L.A. Seeber: Intersuchungen über die Eigenschaften der positiven ternären quadratischen Formen usw”. Göttingsche Gelehrte Anzeigen.
- ^ AnnouncingCompletion
- ^ Weisstein, Eric W. "Sphere packing". mathworld.wolfram.com (英語). 2016年4月12日閲覧。
- ^ Torquato, S.; Stillinger, F. H. (2007). “Toward the jamming threshold of sphere packings: Tunneled crystals”. Journal of Applied Physics 102: 093511. arXiv:0707.4263. Bibcode: 2007JAP...102i3511T. doi:10.1063/1.2802184.
- ^ Chaikin, Paul (June 2007). “Random thoughts”. Physics Today (American Institute of Physics) 60 (6): 8. Bibcode: 2007PhT....60f...8C. doi:10.1063/1.2754580. ISSN 0031-9228.
- ^ Song, C.; Wang, P.; Makse, H. A. (29 May 2008). “A phase diagram for jammed matter”. Nature 453 (7195): 629–632. arXiv:0808.2196. Bibcode: 2008Natur.453..629S. doi:10.1038/nature06981. PMID 18509438.
- ^ Weisstein, Eric W. "Hypersphere Packing". mathworld.wolfram.com (英語).
- ^ Sloane, N. J. A. (1998). “The Sphere-Packing Problem”. Documenta Mathematika 3: 387–396. arXiv:math/0207256v1. Bibcode: 2002math......7256S.
- ^ 宮崎興二『4次元図形百科』丸善出版、2020年、163頁。ISBN 978-4-621-30482-2。
- ^ Cohn, Henry; Kumar, Abhinav (2009), “Optimality and uniqueness of the Leech lattice among lattices”, Annals of Mathematics 170 (3): 1003–1050, arXiv:math.MG/0403263, doi:10.4007/annals.2009.170.1003, ISSN 1939-8980, MR2600869, Zbl 1213.11144 Cohn, Henry; Kumar, Abhinav (2004), “The densest lattice in twenty-four dimensions”, Electronic Research Announcements of the American Mathematical Society 10 (07): 58–67, arXiv:math.MG/0408174, doi:10.1090/S1079-6762-04-00130-1, ISSN 1079-6762, MR2075897
- ^ Miller, Stephen D. (April 4, 2016), The solution to the sphere packing problem in 24 dimensions via modular forms, Institute for Advanced Study. ヴィヤゾフスカの共著者が1時間にわたって証明を解説する動画。
- ^ Klarreich, Erica (March 30, 2016), “Sphere Packing Solved in Higher Dimensions”, Quanta Magazine
- ^ Rogers, C. A. (1947). “Existence Theorems in the Geometry of Numbers”. Annals of Mathematics. Second Series 48 (4): 994–1002. JSTOR 1969390.
- ^ a b O’Toole, P. I.; Hudson, T. S. (2011). “New High-Density Packings of Similarly Sized Binary Spheres”. The Journal of Physical Chemistry C 115 (39): 19037. doi:10.1021/jp206115p.
- ^ Hudson, D. R. (1949). “Density and Packing in an Aggregate of Mixed Spheres”. Journal of Applied Physics 20 (2): 154–162. Bibcode: 1949JAP....20..154H. doi:10.1063/1.1698327.
- ^ Zong, C. (2002). “From deep holes to free planes”. Bulletin of the American Mathematical Society 39 (4): 533–555. doi:10.1090/S0273-0979-02-00950-3.
- ^ Marshall, G. W.; Hudson, T. S. (2010). “Dense binary sphere packings”. Contributions to Algebra and Geometry 51 (2): 337–344.
- ^ “Upper bounds for packings of spheres of several radii” (2012年6月12日). 2013年12月11日閲覧。
- ^ Bowen, L.; Radin, C. (2002). “Densest Packing of Equal Spheres in Hyperbolic Space”. Discrete and Computational Geometry 29: 23–39. doi:10.1007/s00454-002-2791-7.
- ^ Böröczky, K. (1978). “Packing of spheres in spaces of constant curvature”. Acta Mathematica Academiae Scientiarum Hungaricae 32 (3–4): 243–261. doi:10.1007/BF01902361.
- ^ Böröczky, K.; Florian, A. (1964). “Über die dichteste Kugelpackung im hyperbolischen Raum”. Acta Mathematica Academiae Scientiarum Hungaricae 15: 237. doi:10.1007/BF01897041.
- ^ Kozma, R. T.; Szirmai, J. (2012). “Optimally dense packings for fully asymptotic Coxeter tilings by horoballs of different types”. Monatshefte für Mathematik 168: 27. doi:10.1007/s00605-012-0393-x.
- ^ Bezdek, Karoly; Reid, Samuel (2012). Contact Graphs of Sphere Packings Revisited.
- ^ Conway JH, Sloane NJH (1998). Sphere Packings, Lattices and Groups (3rd ed.). ISBN 0-387-98585-9
参考文献[編集]
- Sloane, N. J. A. (1984). “The Packing of Spheres”. Scientific American 250: 116–125. Bibcode: 1984SciAm.250..116G. doi:10.1038/scientificamerican0584-116
 .
. - Weaire, D. L.; Aste, Tomaso (2000). The Pursuit of Perfect Packing. London: Institute of Physics Publishing. ISBN 0-7503-0648-3
- Chaikin, Paul (2007-06). “Reference Frame”. Physics Today 60 (6): 8-9. doi:10.1063/1.2754580
 .
.
外部リンク[編集]
- Dana Mackenzie (May 2002) "A fine mess" (New Scientist) 双曲空間での充填に関する入門的解説
- Weisstein, Eric W. "Circle Packing". mathworld.wolfram.com (英語).
- "Kugelpackungen (Sphere Packing)" (T.E. Dorozinski)
- 3次元球充填アプレット(英語) 球充填のJavaアプレット
- 球による球への最密充填(英語) Javaアプレット
- 球充填のデータベース(英語) (Erik Agrell)







