混成軌道
混成軌道(こんせいきどう、英: Hybrid orbital)とは、原子が化学結合を形成する際に、新たに作られる原子軌道である。典型例は、炭素原子である。炭素は、sp3、sp2、spと呼ばれる、 3 種類の混成軌道を形成することができるが、このことが、有機化合物の多様性に大きく関わっている[1]。混成軌道の概念は、第2周期以降の原子を含む分子の幾何構造と、原子の結合の性質の説明において非常に有用である。
概要[編集]
原子は、混成軌道を形成することにより、化学結合を形成するのに適した状態(原子価結合法において原子価状態と呼ばれる状態)となることができる。新たに作られる軌道は、基本となる軌道とは異なるエネルギーや形状等を持つが、当初、この現象の成因として、異なる種類の軌道が混ぜ合わさったものだと考えられたため、混成(hybridization)と呼ばれるようになった。原子価殻電子対反発則(VSEPR則)と共に教えられることがあるものの、原子価結合および混成はVSEPRモデルとは実際に関係がない[2]。
分子の構造は各原子と化学結合から成り立っているので、化学結合の構造が原子核と電子との量子力学でどのように解釈されるかは分子の挙動を理論的に解明していく上で基盤となる。化学結合を量子力学で扱う方法には主に、分子軌道法と原子価結合法とがある。前者は分子の原子核と電子との全体を一括して取り扱う方法であるのに対して、原子価結合法では分子を、まず化学結合のところで切り分けた原子価状態と呼ばれる個々の原子と価電子の状態を想定する。次の段階として、分子の全体像を原子価状態を組み立てることで明らかにしてゆく。具体的には個々の原子の軌道や混成軌道をσ結合やπ結合の概念を使って組み上げることで、共有結合で構成された分子像を説明していくことになる。それゆえに、原子軌道から原子価状態を説明付ける際に利用する混成軌道の概念は原子価結合法の根本に位置すると考えられている。
歴史[編集]
ライナス・ポーリングは初め、メタン (CH4) といった分子の構造を説明するために混成理論を開発した[3]。この概念はメタンのような単純な化学系のために開発されたが、後により幅広く応用され、今日では有機化合物の構造を合理的に説明する有効な経験則であると考えられている。
混成理論は、分子軌道法ほど、定量的計算には実用的ではない。混成理論の問題点は、配位化学や有機金属化学において結合にd 軌道が関与する場合に特に顕著である。遷移元素化学において混成理論を用いることは可能であるが、一般的に正確ではない。
軌道は分子中の電子の挙動のモデル表現である。単純な混成の場合は、この近似は原子軌道に基づいている。炭素や窒素、酸素のようなより重い原子では、2sおよび2p軌道が原子軌道として用いられる。混成軌道はこれらの原子軌道の混合としたものと仮定され、様々な割合で互いを重ね合わせる。混成理論はこれらの仮定の下において最も適切であり、ルイス構造と等価な単純な軌道の描写を与える。混成は分子を描写するのに必要ではないが、この描写をより簡易に行うことができるようになる。
混成軌道と原子価状態[編集]
炭素の基底状態の電子配置は[He] 2s22p2である。そうすると原子価状態の軌道関数の特性から炭素の結合には2s軌道に帰結するものと、2p軌道に帰結するものの2種類存在することが示唆される。しかし、実際にはダイヤモンドの結晶構造やメタンの構造からは1種類の結合しか存在しないと考えられる。
元々、原子価結合法では水素分子の全電子の状態を表す際に、原子軌道の状態の重ね合わせを原子軌道の一次結合で定式化した。この場合も原子価状態の軌道関数も、2s軌道と2p軌道の重ね合わせで生成する混成軌道関数で定式化することが可能である。そして実際には、混成軌道関数で表される原子価状態は共有結合の方向性とも矛盾しない。
混成軌道の定式化には色々な組み合わせが可能であり、生成した混成軌道は基となった原子軌道(s軌道、p軌道)の名称を使って、sp3軌道(関数)、sp2軌道(関数)、sp軌道(関数)、spd軌道(関数)と呼ばれる。
そして、重ね合わせが可能になるためには原子軌道のエネルギー準位が同程度であることが必要な為、もっぱら主量子数が同じ原子軌道間で混成軌道が生成する。そしてd軌道などについては同一主量子数の軌道よりも、1つ主量子数が大きい原子軌道の方がエネルギー準位差が小さいのでそちらの方の原子軌道と混成することもある。
このように第2周期以降の原子は複数の混成軌道を取ることができ、有機分子や金属錯体などの分子構造の多様性をもたらしている。しかし実際の分子では必ずしも理論的な混成軌道とは異なる結合角を取る場合も多く、非共有電子対が混成軌道に及ぼす立体的な影響は原子価殻電子対反発則として知られている。
sp3混成軌道関数[編集]
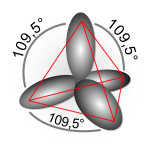
1つのs軌道と3つのp軌道の重ね合わせにより4つの混成軌道が定式化され、sp3混成軌道関数と呼ばれる。次に炭素の場合の例を示す。
これら4つの混成軌道が表す方向性は正四面体の頂点方向と一致し、正四面体中心から各頂点への軸同士の角度は109.5度で交差する。これはメタンの結合角とも合致する。
軌道混成理論によると、メタン中の価電子はエネルギー的に等しくなければならないが、メタンの光電子スペクトルは 12.7 eV(1つの電子対)と23 eV(3つの電子対)の2種のバンドを示す[4][5]。この明らかな矛盾は、sp3軌道が4つの水素原子の軌道と混合した時、さらにもう1つの軌道混合が起こると考えることで説明可能である。
sp2混成軌道関数[編集]
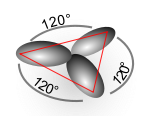
1つのs軌道と2つのp軌道の重ね合わせにより3つの混成軌道が定式化され、sp2混成軌道関数と呼ばれる。次に炭素の場合の例を示す。混成に加わらない軌道(2pz)をz軸に取ると、
これら3つの混成軌道が表す方向性はx-y平面上に互いに120度を成して交差する軌道関数に相当する。これはエチレンの二重結合炭素の結合角とも合致する。
sp混成軌道関数[編集]
1つのs軌道と1つのp軌道の重ね合わせにより2つの混成軌道が定式化され、sp混成軌道関数と呼ばれる。次に炭素の場合の例を示す。混成に加わる軌道(2px)の対象軸をx軸に取ると、
これら2つの混成軌道はx軸上で直線的に対向(180度)する2つの軌道関数に相当する。これはアセチレンが直線状分子であることと合致する。
各軌道混成と分子の形状[編集]
メタンの正四面体型形状で説明されているように、結合間の角度が混成軌道間の角度に(ほぼ)等しいため、軌道混成は分子形状を説明するのを助ける。

| 分類 | spx混成 | sdx混成[6][7][8] | spxdy混成[8] |
|---|---|---|---|
| 典型元素/ 遷移金属 |
遷移金属のみ | ||
| AX2 |
|
||
| AX3 |
|
|
|
| AX4 |
|
|
|
| AX6 |
|
| |
| 軌道間角度[6] | |||
超原子価の混成[編集]
拡張原子価殻[編集]
混成は、ポーリングによって最初に提唱された混成配置を用いて典型元素AX5についてや多くの遷移金属錯体についてしばしば提示される。
| AX5 |
|
|---|---|
| AX6 |
|
| AX7 |
|
反証[編集]
1990年、Magnussonは第二周期元素の超原子価化合物における結合でのd軌道混成の役割を決定的に排除した重要な論文を発表した。超原子価化合物におけるd軌道の関与は長い間、分子軌道理論を用いたこれらの原子の描写における論争および混乱の中心であった。混乱の一部は、これらの化合物を描写するために用いられる基底関数系にd関数を含めなければない点に起因している(さもなければ、不等に高いエネルギーと歪んだ構造が得られる)。また、分子の波動関数へのd関数の寄与は大きい。これらの事実はd軌道が結合に関与しているに違いないことを意味すると誤って解釈されていた[9]。分極関数としてのd関数は、あくまでも他の原子の作る電場により元々の原子軌道が歪む効果を現しているものであり、原子軌道で言うところのd軌道とはやや異なるものである。
共鳴[編集]
計算化学で示されているように、超原子価分子はフッ素や酸素といった電気陰性配位子と強く分極した(そして弱められた)結合を持つ時のみ安定である。これらの配位子は中心原子の原子価電子の占有状態を最大の8個[10]に減らす。これは混成に加えてσ共鳴を含む説明を必要とする。これは、それぞれの共鳴構造が独自の混成配置を持つことを意味する。指針として、全ての共鳴構造は典型元素中心についてはオクテット (8) 則に。
| AX5 | 三方両錐形 |
|---|---|

| |
| AX6 | 八面体形 |
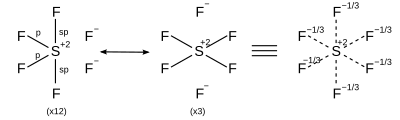
| |
| AX7 | 五方両錐形 |
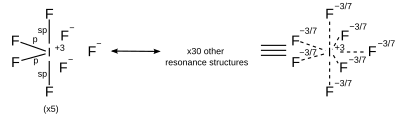
|
等原子価混成[編集]
理想的な混成軌道は有用であるが、現実にはほとんどの結合は中間的な性質の軌道を必要とする。これは、個々の種類 (s, p, d) の原子軌道の柔軟な重み付けを含む拡張を必要とし、分子形状が理想的な結合角からずれた時の結合形成の定量的な描写を可能とする。p性の量は整数値に制限されない。すなわち、sp2.5の様な混成も容易に記述できる。
結合軌道の混成はベント則によって決定される。
孤立電子対を持つ分子[編集]
孤立電子対を持つ分子では、σ孤立電子対および結合性電子対は様々な度合いで混成し[11]分子の結合角を与える。例えば、水における酸素の2つの結合を形成する混成軌道はsp4.0と説明でき、104.5° の軌道間角を与える。これは、20%のs性と80%のp性を持つことを意味し、混成軌道が1つのs軌道と4つのp軌道から形成されたことを意味している訳ではない。
多重結合に類似したやり方で、孤立電子対はσおよびπ対称性に照らして区別される。例えば、水では2つの孤立電子対の1つはH-O-H骨格に垂直な電子密度を持つ純粋なp型軌道であるのに対して[11][12]、もう一方の孤立電子対はH-O-H結合と同一平面にあるs性の高い軌道である[11][12]。
超原子価分子[編集]
孤立電子対を持つ超原子価分子では、結合スキームは超原子価要素と等原子価結合性混成から成る要素に分解することができる。超原子価要素はp軌道を使用した共鳴結合から成る。
| 等原子価結合性混成軌道の数(赤色) | ||||
|---|---|---|---|---|
| 2 | 1 | - | ||
| 超原子価要素 | 直線形軸(1つのp軌道) | シーソー形 | T字形 | 直線形 |

|

|

| ||
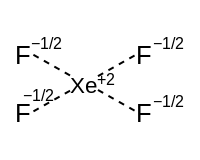
| 平面四角形赤道(2つのp軌道) | - | 四角錐形 | 平面四角形 | |

|
| |||
| 平面五角形赤道(2つのp軌道) | - | 五角錐形 | 平面五角形 | |

|

| |||
混成異常[編集]
有効なspxを作るためのsならびにp軌道の混成は、それらが同等な動径方向広がりを持つことを必要とする。2p軌道が2s軌道よりも平均して10%弱大きい(部分的には2p軌道が〔自明な原点の節を除いて〕動径節を持たないことに起因する)のに対して、1つの動径節を持つ3p軌道は3s軌道よりも20-33%大きい[13]。sならびにp軌道の広がりの差は周期表の下にいく程大きくなる。化学結合における原子の混成は局在化分子軌道を考えることによって解析できる(例えば自然結合軌道(NBO)スキームにおける自然局在化分子軌道を使う)。メタン(CH4)では、計算されたp/s比は約3であり、「理想的な」sp3混成と一致しているが、シラン(SiH4)ではp/s比は2に近い。同様の傾向がその他の2p元素についても見られる。水素のフッ素への置換はp/s比をさらに低下させる[14]。2p元素は直交する混成軌道を持つ理想に近い混成を示す。より重いPブロック元素では、この直交性の過程は正当化できない。理想的な混成からのこれらのずれはヴェルナー・クツェルニクによって混成異常と命名された[15]。
光電子スペクトル[編集]
混成軌道の概念は多くの分子の紫外光電子スペクトルを誤って予測するという広く信じられている間違った考えが存在する。これは、クープマンズの定理が局在化軌道に適用されるとすれば真実であるが、量子力学は(この場合イオン化した)波動関数が分子の対称性(原子価結合理論における共鳴を意味する)に従うことを必要とする。例えば、メタンでは、イオン化状態 (CH4+) は、追い出された電子が4つのσ結合のそれぞれに起因すると考える4つの共鳴構造から構築することができる。構造の数を保存するこれらの4つの共鳴構造の線形結合から、三重に縮退したT2状態と1つのA1状態が導かれる[16]。それぞれのイオン化状態と基底状態との間のエネルギー差はイオン化エネルギーに相当し、実験と一致する2つの値が得られる。
混成理論と分子軌道理論[編集]
混成理論は有機化学の不可欠な部分であり、一般的に分子軌道理論と共に説明される。反応機構を描くためには、2つの原子が2つの電子を共有している古典的な結合描写が必要なことがある[17]。メタンの結合角を分子軌道理論によって予測するのは直接的ではない。混成理論はアルケン[18]やメタン[19]における結合を説明する。
混成原子軌道から作られた結合性軌道は局在化分子軌道と考えられる。分子軌道理論では、適切な数学的変換(ユニタリ変換)によって非局在化軌道から結合性軌道を作ることができる。基底状態で閉殻構造にある分子では、行列式の性格からこの数学的変換は総体の多電子波動関数を変化させない(個々の軌道のエネルギーは変化するが分子全体のエネルギーは変化しない)。したがって、基底状態の総エネルギーと電子密度、総エネルギーの最低値と対応する分子構造を説明するための、基底状態を描写する混成軌道は、非局在化軌道による描写と「等価」である。WeinholdとLandisは自然結合軌道の文脈内での軌道混成概念の適切な(対称性に適した)使用について述べている[20]。自然結合軌道は、古典的な(原子価結合/ルイス構造)結合性電子対および孤立電子対の現代的な類似体を含む局在化軌道理論である。例えば、フッ化水素分子では、2つのF孤立電子対は本質的に混成していないp軌道であるのに対して、残りの1つはsp混成軌道である。類似の考察は水にも適用できる(1つのO孤立電子対が純粋なp軌道で、もう1つがspx 混成軌道)。
脚注[編集]
- ^ “サルにはできない有機化学”. 早稲田大学 細川誠二郎研究室. 2020年7月26日閲覧。
- ^ Gillespie, R.J. (2004), “Teaching molecular geometry with the VSEPR model”, Journal of Chemical Education 81 (3): 298–304, Bibcode: 2004JChEd..81..298G, doi:10.1021/ed081p298
- ^ Pauling, L. (1931), “The nature of the chemical bond. Application of results obtained from the quantum mechanics and from a theory of paramagnetic susceptibility to the structure of molecules”, Journal of the American Chemical Society 53 (4): 1367–1400, doi:10.1021/ja01355a027
- ^ “Molecular Orbitals of Methane (CH4) and Photon Electron Spectrum” (PDF). 2011年7月29日閲覧。
- ^ “photoelectron spectrum of methane” (JPEG). 2011年7月29日閲覧。
- ^ a b Weinhold, Frank; Landis, Clark R. (2005). Valency and bonding: A Natural Bond Orbital Donor-Acceptor Perspective. Cambridge: Cambridge University Press. pp. 367, 381–383. ISBN 978-0-521-83128-4
- ^ Kaupp, Martin (2001). “"Non-VSEPR" Structures and Bonding in d(0) Systems”. Angew Chem Int Ed Engl. 40 (1): 3534–3565. doi:10.1002/1521-3773(20011001)40:19<3534::AID-ANIE3534>3.0.CO;2-#.
- ^ a b Bayse, Craig; Hall, Michael (1999). “Prediction of the Geometries of Simple Transition Metal Polyhydride Complexes by Symmetry Analysis”. J. Am. Chem. Soc. 121 (6): 1348–1358. doi:10.1021/ja981965+.
- ^ Magnusson, E. (1990). “Hypercoordinate molecules of second-row elements: d functions or d orbitals?”. J. Am. Chem. Soc. 112: 7940-7951. doi:10.1021/ja00178a014.
- ^ David L. Cooper , Terry P. Cunningham , Joseph Gerratt , Peter B. Karadakov , Mario Raimondi (1994). “Chemical Bonding to Hypercoordinate Second-Row Atoms: d Orbital Participation versus Democracy”. Journal of the American Chemical Society 116 (10): 4414–4426. doi:10.1021/ja00089a033.
- ^ a b c Allen D. Clauss, Stephen F. Nelsen, Mohamed Ayoub, John W. Moore, Clark R. Landis and Frank Weinhold (2014). “Rabbit-ears hybrids, VSEPR sterics, and other orbital anachronisms”. Chemistry Education Research and Practice 15: 417–434. doi:10.1039/C4RP00057A.
- ^ a b Laing, Michael (1987). “No rabbit ears on water. The structure of the water molecule: What should we tell the students?”. J. Chem. Educ. 64: 124–128. doi:10.1021/ed064p124.
- ^ Kaupp, Martin (2007). “The role of radial nodes of atomic orbitals for chemical bonding and the periodic table”. J. Comput. Chem. 28 (1): 320–325. doi:10.1002/jcc.20522. ISSN 0192-8651.
- ^ Kaupp, Martin (2014) [1st. Pub. 2014]. “Chapter 1: Chemical bonding of main group elements”. In Frenking, Gernod & Shaik, Sason. The Chemical Bond: Chemical Bonding Across the Periodic Table. Wiley-VCH. ISBN 978-1-234-56789-7
- ^ Kutzelnigg, W. (1988). “Orthogonal and non-orthogonal hybrids”. J. Mol. Struct. THEOCHEM 169: 403–419. doi:10.1016/0166-1280(88)80273-2.
- ^ Sason S. Shaik; Phillipe C. Hiberty (2008). A Chemist's Guide to Valence Bond Theory. New Jersey: Wiley-Interscience. ISBN 978-0-470-03735-5
- ^ Clayden, Jonathan; Greeves, Nick; Warren, Stuart; Wothers, Peter (2001). Organic Chemistry (1st ed.). Oxford University Press. p. 105. ISBN 978-0-19-850346-0.
- ^ Organic Chemistry, Third Edition Marye Anne Fox James K. Whitesell 2003 ISBN 978-0-7637-3586-9
- ^ Organic Chemistry 3rd Ed. 2001 Paula Yurkanis Bruice ISBN 0-13-017858-6
- ^ Weinhold, Frank; Landis, Clark R. (2012). Discovering Chemistry with Natural Bond Orbitals. Hoboken, N.J.: Wiley. pp. 67-68. ISBN 978-1-118-11996-9













