標準模型の歴史
この記事の正確性に疑問が呈されています。 |
この記事には独自研究が含まれているおそれがあります。 |
| 標準模型 | ||||||||
|---|---|---|---|---|---|---|---|---|
| ||||||||
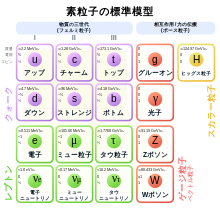
| 標準模型の素粒子 | ||||||||
| ||||||||
標準模型の歴史(ひょうじゅんもけいのれきし)は、現在の素粒子モデルの標準となっている標準模型が構築された歴史について記述する。
背景[編集]
標準模型は、素粒子物理学の三つの基本的な力すなわち強い力、弱い力、電磁力を記述する理論である。標準模型は、強い力の量子色力学と、弱い力、電磁力のワインバーグ=サラム理論と小林・益川理論を合わせたものとなっている。また、ワインバーグ=サラム理論の基礎には、量子電磁力学がある。
この理論は場の量子論的方法で記述されているため、量子力学と特殊相対性理論の両方と整合している。今までのところ、三つの力に関するほとんどすべての実験結果は標準模型による予言と一致する。ただし、ニュートリノは質量ゼロの粒子として定義しているため、ニュートリノ振動などの実験結果を説明するためには修正が必要である。
したがって、標準理論は基本的な力の完全な理論ではない。その理由として、先の三つの力の統一ができていないことがあげられる(「大統一理論」、「超対称大統一理論」を参照)。さらに、重力について何も記述していないことも大きな問題である。現在も標準模型を超えたより完全な素粒子模型の研究が活発に進められている。
電磁気力:量子電磁力学[編集]
量子電磁力学は、場の量子論の枠組みで古典電磁力学を記述しなおすものである。場の量子論は、第二量子化、生成消滅演算子、繰り込み、ゲージを導入することで成立している。
電磁場の量子化[編集]
1927年から1928年、ポール・ディラックによる古典電磁気学の量子化、オスカル・クライン、パスクアル・ヨルダン、ウィグナー、およびウラジミール・フォックによる生成消滅演算子の形成がなされる[1]。また、場の第二量子化を導入することで場の量子論をヴェルナー・ハイゼンベルク、ヴォルフガング・パウリが創る。ここで、粒子n個の確率波の量子論は、次元が4n次元(配位空間)で、空間で再量子化すると、特殊相対論を満たす4次元空間に戻る(ハイゼンベルクとパウリの場の量子論は、ディラック方程式と同等であることが判明)。
こうして、パウリ、ハイゼンベルク、ユージン・ウィグナー、パスクアル・ヨルダンらの尽力により量子電磁力学の定式化が始まり、1932年のエンリコ・フェルミの論文[2]などによって定式化がなされた。
発散問題[編集]
当時は光子や荷電粒子を含むような計算も原理的には可能であると思われていたが、次第に計算結果が無限大に発散することが問題となった。場の量子論における発散問題は1930年代初頭にロバート・オッペンハイマー[3]や他の多くの物理学者によって初めて認識され、フェリックス・ブロッホとアーノルド・ノルドジークの研究[4](1937年)やヴィクター・ワイスコフの研究[5](1939年)では、この計算が摂動展開の1次においてのみ成功するが、高次の級数においては無限大が現れることが指摘された。有限の物理量を求めるための計算結果に無限大が現れることは物理法則としての致命的な矛盾である。
初期の理論[編集]
1939年、最初の繰り込みのアイデアに迫る論文がダンコフ(発想1937年)によって発表された。この論文は、計算間違いが含まれていたため計算結果の無限大を回避できていないものであった。後に朝永振一郎は、計算ミスに気付き修正したため、繰り込みに到達することができた[6]。
朝永の超多時間理論[編集]
- 量子電磁力学の「相対論的共変形式・ゲージ形式」の確立、繰り込みへの助走[7]
理論的背景[編集]
当時問題となっていた場の量子論の計算結果の発散を解決するには、ローレンツ変換に対する不変性―対称性―共変性を式に与えることが、式の見通しを良くするために必要であった。従来の場の量子論は、共変形式を満たさず計算が困難である。朝永は、以下の方法で場の量子論を共変的に書き換え、特殊相対論的なゲージ理論を確立する。
朝永の超多時間理論は、光速以下では結ばれないミンコフスキー空間的超曲面を、場の量子論に導入する。量子力学では、場の量はすべて交換可能で、確率振幅(状態)が与えられるので、従来の一個の時間であった超平面が、連続無限個の時間を与える超曲面での関数となる。これにより、1個の時間に関する確率振幅の微分方程式(シュレディンガー方程式)が、空間的超曲面でのローレンツ系に依存しない汎関数微分方程式に置き換えられる。
これは、1932年にディラックが提唱した多時間理論(相互作用をしている電子一つ一つに独立な時間を与える)の電子の生成・消滅を含まないという欠点を改めたものであるため、超多時間と名付けられた。
演算子・相互作用切り出し[編集]
さらに、朝永表示(相互作用表示-シュウィンガー表示)を得る。これらにより、見通しよく簡素化された共変形式が確立され、繰り込みを確立する手段が整う。この場の量子論の進展により、式の扱いが容易になった時点で、朝永はすでに繰り込みの着想を得ていたようである。朝永が最初の繰り込みの考えを得たのは超多時間理論の確立から遡る1938年である[7]。
繰り込み・可換ゲージ[編集]
1943年の超多時間論で、繰り込みや可換ゲージを記述する準備がなされ、1947年以降、繰り込みや、量子電磁力学の可換ゲージ記述が確立される。
ファインマンの経路積分[編集]
- 「新しい量子形式」と量子電磁力学の確立、繰り込みへの助走
リチャード・ファインマンは、ポール・ディラックの著書[8]中の、「 は に対応する(L はラグランジアン)」という箇所にある指摘に興味をそそられ、ここから発想を得たと言われている。
具体的な経路積分の発想は、二重スリット実験と関連する。二重スリット実験ではスリットの数は2つであるが、これを無限個に拡張した考え方が経路積分である。経路積分は、現在用いられている一般的な方法になっている。
精密実験[編集]
第二次世界大戦を経てマイクロ波技術の進歩により水素原子のエネルギー準位の縮退からのずれ(ラムシフト)[9]や電子の異常磁気モーメント[10]をより精密に測定することが可能(1947年)になると、これらの実験により既存の理論では説明することのできない現象の存在が明らかとなった。
非相対論的繰り込み[編集]
実験結果を受けて、ハンス・ベーテはシェルターアイランド会議に出席した帰りに、スケネクタディからニューヨークへ向かう汽車の中で[11]、水素原子の「非相対論的」なエネルギー準位について計算方法を考え、論文[12]を提出した。ベーテの計算では、質量と電荷に無限大の補正を加えることで、無限大が相殺し最終的に有限の物理量が導出された。これは、無限大の発散を回避する繰り込みの操作であった。しかし、この計算は特殊相対論を導入していない非相対論的繰り込みであり、実験とは一致しなかった。より厳密な相対論的な繰り込み理論の確立には、超多時間論や経路積分により、場の量子論を大幅に書き換える必要があった。
繰り込みの確立[編集]
超多時間理論(1943年)、相互作用表示(1947年)、経路積分(1948年)で相対論的な量子電磁力学を確立した、朝永振一郎[13]、ジュリアン・シュウィンガー[14][15]、リチャード・ファインマン[16][17][18]、フリーマン・ダイソン[19][20]らは、ラムシフトの理論的計算に取り組む。以前から、ベーテと同様の考えを持っていた朝永は超多時間理論を駆使し、同様にシュウィンガーやファインマンもそれぞれの理論で1948年には完全な形で繰り込みを完成させていた。彼らの計算結果は、摂動展開の全てのオーダーにおいて観測される物理量が有限(34桁の精度という驚異的な値)となる定式化であった。
超多時間論または経路積分による相対論的に共変な場の量子論の確立と、これを基にした繰り込みによる量子電磁力学のにより朝永、シュウィンガー、ファインマンの3人は1965年にノーベル物理学賞を受賞した。ファインマンによるファインマン・ダイアグラムを用いた数学的なテクニックは、朝永とシュウィンガーの演算子を用いる計算方法と異なるように見えたが、後にフリーマン・ダイソンはこの2つのアプローチが数学的に等価であることを証明した。
その後の発展[編集]
繰り込みの原理解釈[編集]
量子化や生成消滅演算子に加え、繰り込みによって、素粒子論の規範となる量子電磁気学は確立され、同時に、素粒子論の最も基本となる場の量子論も確立された。そのため、繰り込みは理論の妥当性を保証するために必要不可欠な操作、すなわち原理であるとする解釈。
繰り込みの数学的解釈[編集]
繰り込みの導入によって物理的な矛盾は解消できたが、数学的な理論付けは未だなされていない。ファインマン自身、その数学的な妥当性については最後まで満足せずに、"shell game"(いんちき)、"hocus pocus"(奇術)のようだと自著で述べている[21]。
場の量子論とゲージ理論の拡張[編集]
量子電磁力学 (QED) はその後に発展する場の量子論に関する数々の理論の基礎的なモデルとなる。QEDの完結性・完全性(34桁の精度で実験と理論が一致)は原理としての有効性を認識させた。QEDの確立に用いられた「場の量子論・特殊相対論・繰り込み・ゲージ理論・対称性」の記述原理に従い、他の2つの力(強い力と弱い力)が理論化されることになる。量子色力学とワインバーグ=サラム理論の形成には、QED可換ゲージを拡張した非可換ゲージ理論、QED繰り込みを拡張した繰り込み群が用いられた。
弱い力 : ワインバーグ・サラム理論[編集]
原型[編集]
弱い力は、エンリコ・フェルミによるベータ崩壊(1934年)を端緒とする。この理論をゲージ理論で基礎付ける試みは長い間うまくいかず、量子電磁力学と結びつけることで成功した。先にも述べたように、量子電磁力学は、素粒子の満たすべきすべての原理から構成されている。
ゲージ[編集]
強い力と同じ。上に記載のゲージや強い力のゲージ参照。
非可換ゲージとヘーラルト・トホーフトによる非可換ゲージの繰り込み可能性が、量子色力学とワインバーグ=サラム理論両方の基礎にある。
基礎[編集]
1961年にシェルドン・グラショウが電磁相互作用と弱い相互作用を統一して記述する電弱統一理論の基礎を構築した。
対称性の自発的破れ[編集]
この成功の鍵は、南部陽一郎による超伝導理論を元にした、自発的対称性の破れ1960年である(ちなみに、朝永振一郎の中間結合論が、超伝導にの3個の原理のひとつに使われる)。対称性の自発的破れを元に、1964年にフランソワ・アングレール、ロベール・ブルー[22]、ゲラルド・グラルニク、カール・リチャード・ハーゲン、トム・キッブル[23][24]、ピーター・ヒッグスによって粒子に質量を与えるヒッグス機構が考案された。南部は自発的対称性の破れで、益川・小林と共にノーベル賞を受賞した。
完成[編集]
1967年、グラショウの理論に自発的対称性の破れによる質量獲得を示すヒッグス機構を加え、スティーヴン・ワインバーグとアブドゥッサラームが独立して、電弱統一理論を完成させた。(宇宙開闢の超高温で質量を失い相互作用の区別がなくなる現象も示す)。グラショウ、サラム、およびワインバーグはこの功績でノーベル賞を受賞している。
強い力 : 量子色力学[編集]
原型[編集]
一方、強い相互作用の原型は、1935年湯川の「強い力の場の理論」すなわち中間子論である。湯川モデルは、ニールス・ボーア、ヴェルナー・ハイゼンベルク等の反対を受けた。しかし、原理「素粒子と力の場の対応」は、中間子の発見を機に、一般に認められる。
現代的な強い相互作用は、強い力を構成する粒子クォークをその足場にしている。
クォーク[編集]
クォーク模型に至る道は、20年に至る道のりであった。小林稔の2中間子仮説を、わずかばかり修正し、坂田の2中間子仮説が出る。その後、多くの素粒子を分類・理論化する試みがなされ(1949年2粒子からなるヤン・フェルミ模型など)、1953年にマレー・ゲルマン、西島和彦らのストレンジネスの同時発見がなされる。これらを元に、1955年に坂田昌一が坂田模型を発表し、大貫義郎らが、群論を使いSU(3)モデル(IOO対称性)を示す。(クォーク模型において群論を使った嚆矢)。[25] さらに、八道説(日本でも唱えられている)を経て、マレー・ゲルマン、ジョージ・ツワイク、ユヴァル・ネーマンが1964年、独立してクォークを示し、長い素粒子を整理する戦いは終わる。量子色力学は、クォークの3要素(電荷1/3)に対応するよう構成されることになる。これによりゲルマンはノーベル賞を受賞。
ゲージ[編集]
クォークが構造的基礎であったのに対し、理論的基礎はゲージと繰り込み・繰り込み群であった。1927年のフリッツ・ロンドンのゲージ、1948年の朝永振一郎の(QEDの)可換ゲージを経て、1954年の楊振寧とロバート・ミルズの非可換ゲージ理論[26]が強い力(量子色力学)のゲージとして発表される。
カラー[編集]
クォーク理論が完成したと同年の1964年、オスカル・グリーンバーグ[27]、韓茂栄、南部陽一郎[28]宮本米二、堀尚一[29]が独立してカラーを提唱し[30]、1971年ヘーラルト・トホーフトが非可換ゲージ場のくり込み可能性を証明する。[31][32]
完成[編集]
1973年、H. デビッド・ポリツァー、デイビッド・グロス、 フランク・ウィルチェック[33][34][35]が、繰り込み群を駆使した漸近的自由性の研究によって非可換ゲージ理論を完成させ、量子色力学は強い相互作用の基礎理論としての地位を固めた。(繰り込み群が本格的に使われた最初。師匠のゲルマンが繰り込みの走りを形成し、漸近自由による非可換ゲージ完成に、ゲルマンも参加)
繰り込み群による非可換ゲージでの漸近自由で、ポリツァー、グロス、ウィルチェック、繰り込み可能でトホーフトが、それぞれノーベル賞を受ける。
CP対称性の破れ:小林・益川理論[編集]
小林誠および益川敏英は、もしクォークが3世代(6種類)以上存在し、クォークの質量項として世代間の混合を許すもっとも一般的なものを考えるならば、既にK中間子の崩壊の観測で確認されていたCP対称性の破れを理論的に説明できることを示した。
クォークの質量項に表れる世代間の混合を表す行列はカビボ・小林・益川行列(CKM行列)と呼ばれる。2世代の行列理論をニコラ・カビボが1963年に提唱し、3世代混合の理論を1973年に小林・益川の両者が提唱した。
発表当時クォークはアップ、ダウン、ストレンジの3種類しか見つかっていなかったが、その後、1995年までに残りの3種類(チャーム、ボトム、トップ)の存在が実験で確認された。
現在KEKのBelle実験およびSLACのBaBar実験で、この理論の精密な検証が行われている。
これらの実験により小林・益川理論の正しさが確かめられ、2008年、小林、益川両名にノーベル物理学賞が贈られた。
標準模型を超えて[編集]
脚注[編集]
- ^ P.A.M. Dirac (1927). “The Quantum Theory of the Emission and Absorption of Radiation”. Proceedings of the Royal Society of London A 114: 243–265. doi:10.1098/rspa.1927.0039.
- ^ E. Fermi (1932). “Quantum Theory of Radiation”. Reviews of Modern Physics 4: 87–132. doi:10.1103/RevModPhys.4.87.
- ^ R. Oppenheimer (1930). “Note on the Theory of the Interaction of Field and Matter”. Physical Review 35: 461–477. doi:10.1103/PhysRev.35.461.
- ^ F. Bloch, A. Nordsieck (1937). “Note on the Radiation Field of the Electron”. Physical Review 52: 54–59. doi:10.1103/PhysRev.52.54.
- ^ V. F. Weisskopf (1939). “On the Self-Energy and the Electromagnetic Field of the Electron”. Physical Review 56: 72–85. doi:10.1103/PhysRev.56.72.
- ^ くりこみ理論のころ
- ^ a b
田地隆夫「超多時間理論(<特集>朝永振一郎博士の業績をふりかえって)」『日本物理學會誌』第35巻第1号、社団法人日本物理学会、1980年1月5日、65-67頁、NAID 110002068201。
伊藤大介「くりこみ理論の建設(<特集>朝永振一郎博士の業績をふりかえって)」『日本物理學會誌』第35巻第1号、社団法人日本物理学会、1980年1月5日、67-71頁、NAID 110002068202。 - ^ P.A.M.Dirac『The Principles Of Quantum Mechanics』みすず書房 (1983) V.The Equations Of Motion Ş32 P.128
- ^ W. E. Lamb, R. C. Retherford (1947). “Fine Structure of the Hydrogen Atom by a Microwave Method,”. Physical Review 72: 241–243. doi:10.1103/PhysRev.72.241.
- ^ P. Kusch, H. M. Foley (1948). “On the Intrinsic Momement of the Electron,”. Physical Review 73: 412. doi:10.1103/PhysRev.74.250.
- ^ Schweber, Silvan (1994). “Chapter 5”. QED and the Men Who Did it: Dyson, Feynman, Schwinger, and Tomonaga. Princeton University Press. p. 230. ISBN 978-0691033273
- ^ H. Bethe (1947). “The Electromagnetic Shift of Energy Levels”. Physical Review 72: 339–341. doi:10.1103/PhysRev.72.339.
- ^ S. Tomonaga (1946). “On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields”. Progress of Theoretical Physics 1: 27–42. doi:10.1143/PTP.1.27.
- ^ J. Schwinger (1948). “On Quantum-Electrodynamics and the Magnetic Moment of the Electron”. Physical Review 73: 416–417. doi:10.1103/PhysRev.73.416.
- ^ J. Schwinger (1948). “Quantum Electrodynamics. I. A Covariant Formulation”. Physical Review 74: 1439–1461. doi:10.1103/PhysRev.74.1439.
- ^ R. P. Feynman (1949). “Space-Time Approach to Quantum Electrodynamics”. Physical Review 76: 769–789. doi:10.1103/PhysRev.76.769.
- ^ R. P. Feynman (1949). “The Theory of Positrons”. Physical Review 76: 749–759. doi:10.1103/PhysRev.76.749.
- ^ R. P. Feynman (1950). “Mathematical Formulation of the Quantum Theory of Electromagnetic Interaction”. Physical Review 80: 440–457. doi:10.1103/PhysRev.80.440.
- ^ F. Dyson (1949). “The Radiation Theories of Tomonaga, Schwinger, and Feynman”. Physical Review 75: 486–502. doi:10.1103/PhysRev.75.486.
- ^ F. Dyson (1949). “The S Matrix in Quantum Electrodynamics”. Physical Review 75: 1736–1755. doi:10.1103/PhysRev.75.1736.
- ^ Feynman, Richard (1985). QED: The Strange Theory of Light and Matter. Princeton University Press. p. 128. ISBN 978-0691125756
- ^ Englert, François; Brout, Robert (1964). “Broken Symmetry and the Mass of Gauge Vector Mesons”. Physical Review Letters 13: 321–23. doi:10.1103/PhysRevLett.13.321
- ^ G.S. Guralnik, C.R. Hagen, T.W.B. Kibble (1964). “Global Conservation Laws and Massless Particles”. Physical Review Letters 13: 585–587. doi:10.1103/PhysRevLett.13.585.
- ^ G.S. Guralnik (2009). “The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles”. International Journal of Modern Physics A 24: 2601–2627. doi:10.1142/S0217751X09045431. arXiv:0907.3466.
- ^ 大貫義郎「対称性理論事始」『素粒子論研究』第82巻第6号、素粒子論グループ 素粒子研究編集部、1991年3月20日、503-547頁、NAID 110006408072。
- ^ Yang, C. N.; Mills, R. (1954), “Conservation of Isotopic Spin and Isotopic Gauge Invariance”, Physical Review 96 (1): 191–195, doi:10.1103/PhysRev.96.191
- ^ O. W. Greenberg Spin and Unitary-Spin Independence in a Paraquark Model of Baryons and Mesons Physical Review Letters 13(1964) 598-602
- ^ M.Y. Han, Y. Nambu (1965). “Three-Triplet Model with Double SU(3) Symmetry”. Physical Review 139: B1006. doi:10.1103/PhysRev.139.B1006.
- ^ 小川修三「坂田学派と素粒子模型の進展」『日本物理學會誌』第51巻第2号、社団法人日本物理学会、1996年2月5日、90-94頁、NAID 110002068935。
- ^ 実教出版
- ^ 't Hooft, G. (1971). “Renormalization of massless Yang-Mills fields”. Nuclear Physics B 33: 173–177. doi:10.1016/0550-3213(71)90395-6.
- ^ 't Hooft, G. (1971). “Renormalizable Lagrangians for massive Yang-Mills fields”. Nuclear Physics B 35: 167–448. doi:10.1016/0550-3213(71)90139-8.
- ^ D.J. Gross, F. Wilczek (1973). “Ultraviolet behavior of non-abeilan gauge theories”. Physical Review 30: 1343–1346. doi:10.1103/PhysRevLett.30.1343.
- ^ H.D. Politzer (1973). “Reliable perturbative results for strong interactions”. Physical Review Letters 30: 1346–1349. doi:10.1103/PhysRevLett.30.1346.
- ^ W. Bardeen, H. Fritzsch, M. Gell-Mann (1973). "Light cone current algebra, π0 decay, and e+ e− annihilation". In R. Gatto (ed.). Scale and conformal symmetry in hadron physics. John Wiley & Sons. p. 139. arXiv:hep-ph/0211388. ISBN 0-471-29292-3。

![{\displaystyle \exp {\left[i\int _{t_{1}}^{t_{2}}{\frac {L_{\text{classic}}\left(x,{\dot {x}}\right)\,dt}{\hbar }}\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae55114aa507e135f485d03fe285d3346a61e850)
