ボロミアン環
ボロミアン環(ボロミアンかん、英: borromean ring)、もしくはボロメオの環、ボロミアンリングとは、どの輪(結び目)を外しても他の輪が分離可能となる、結び目理論における絡み目である。 どの2つの輪もホップリンクにはなっていないにもかかわらず、分離不可能な絡み目となっている。 また、ボロミアンリンクの最も単純な例である。
数学的特徴
[編集]理想的な円環での構成不可能性
[編集]ボロミアン環は右図のようによく理想的な円環によって描かれることが多いが、実際には幾何学的に理想的な円環では構成できない。

フリードマンとスコラはボロミアン環を含む絡み目が理想的な円環で構成不可能であることを証明した。輪1と輪2が2カ所で交差していると仮定すると、輪1と輪2は平面か球面上に存在することとなる。しかしこの場合に輪3がボロミアン環を構成するためには、平面か球面と4回交差する必要があり、そのような輪は存在しない(Lindström & Zetterström 1991)。


しかし、右図に示すように楕円を用いればボロミアン環は構成できる。楕円の偏心率はいくらでも小さくできるため、ほとんど円形によって構成することは可能である。
八面体グラフとの関連
[編集]3つの輪があり、それぞれが交差するために図のように8つの領域に分けられる。この領域を面と捉え、それぞれの交差を頂点と捉えることで、八面体グラフと対応する。 そして八面体グラフから考えると、全ての頂点において4本の辺が接続しており、辺を3色に塗り分けることでそれぞれの頂点において輪の重なりを示せる。 ボロミアン環は交互に頂点の上下を通過し、その結果3本の独立した輪が形成される[1]。
絡まり
[編集]結び目理論において、ボロミアン環はボロミアンリンク(任意の2つの輪は分離可能であるが、全体は分離可能ではない)の簡潔な例である。このグラフには様々な見方ができる。
1つ目の見方は群論を用いた見方である。2つの輪の絡み目補空間の基本群が、ザイフェルト–ファン・カンペンの定理によって2つの生成子aとbの自由群となる。この場合、3つめの輪が交換子[a, b] = aba-1b-1を持つ。これは輪の上下を通ることに対応しているが、これは基本群では自明ではないためボロミアン環は分離不可能である。
他にも、補空間のコホモロジーは非自明なMassey productを台とするが、これは分離可能な場合とは異なる。Massey productの単純な例であり、この代数は幾何学と対応する。3-fold Massey productとは2-fold Massey productが存在しない場合にのみ定義される積であり、ボロミアン環の2つの輪が分離可能である(=2-fold Massey productが存在しない)性質に対応しており、3-fold Massey productが存在する性質が3つの輪は分離不可能である事を示している。
数論トポロジーでは、整数環のイデアルは、絡み目と対応し、素イデアルは結び目と対応する。3つの素数(13, 61, 937)は2で割ったあまりにリンクしているが、どの2つの素数同士もリンクしていない(ルジャンドル記号は1である)。したがって、これらの素数は2を法とする"proper Borromean triple"[2] や、"mod 2 Borromean primes"と呼ばれる[3]。
双曲幾何学
[編集]ボロミアン環は双曲結び目である。三次元球面内のボロミアン環の補空間は完備双曲計量として有限な体積(双曲体積)を持つ。ボロミアン環の双曲体積は16Л(π/4) = 7.32772… (ただし Л はロバチェフスキー関数である)となる[4]。
名称と歴史
[編集]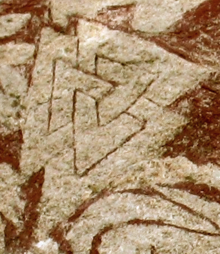
ボロミアン環という名称は北イタリアの貴族であるボッロメオ家の紋章からきている。 ボロミアン環自体はより古くから使われており、7世紀のノース人の絵画石碑にも見られる。

ボロミアン環は結束力の象徴として宗教や芸術など様々な文脈で用いられてきた。その中でも特にトリニティの象徴として用いられた。精神分析家のジャック・ラカンはボロミアン環は人の心を現実界・象徴界・想像界の3つに分類し、晩年のラカンはこれら3界の関係をボロミアン環で表した。
バランタイン・ブルワリーのロゴにも用いられており、現在でもビールのロゴに残っている[5]。
ボロミアン環の数学的な特性についてマーティン・ガードナーは1961年にサイエンティフィック・アメリカンで取り上げた。
2006年には国際数学連合がボロミアン環を連合のロゴに決定した[6]。
インドでは、6世紀以前のティルバンミュールにあるマランディズワラ寺院の石柱にも似た図形が見られる[7][8]
ボロミアン環に類似した図形
[編集]
中世およびルネッサンス期のヨーロッパでは、ボロミアン環が2次元に落とし込まれた図形である、3つの要素が絡み合って見える図形が数多く見られる。しかしそれらは「閉じて」いないため、正確にはボロミアン環とは異なる。 スノルデレブ・ ストーン(ヴァイキング時代のルーン石碑)では動物の角がボロミアン環のように絡み合い、ディアーヌ・ド・ポワチエのエンブレムでは三日月がボロミアン環のように絡み合っている。少し異なるが、SCインテルナシオナルのロゴや三つ巴、ベン図も図形的に類似している。
同様に、猿のこぶし結びも3重になっているにもかかわらず本質的にはボロミヤ環の3次元表現とされる。 不完全なボロミアン環のような支持関係によって、3本のコップのうえの3本のナイフからなる台にグラスを乗せることができる[9]。
4つ以上の輪からなるボロミアン環
[編集]
結び目理論においては、ボロミアン環の輪が増えたものをmultiple ボロミアン環と読んでおり、5つの輪からなる図は不和主義(Discordianism)の象徴であり、Principia Discordiaに描かれている。
組み紐
[編集]
ボロミアン環の輪を切断すると、三つ編みの1ユニットとなる。そして逆に、三つ編みの1ユニットの両端を結ぶとボロミアン環となる。ボロミアン環の輪のいずれかを除去すると残りの輪が分離可能であるのと同様、三つ編みも1本の紐を除去すると残り2本の紐は分離可能である。これらはそれぞれボロミアンリンクとボロミアンブレイドと呼ばれている。
ボロミアン環の輪同士は輪環の順を形成しており、非推移的である。上の図を用いて説明すると、赤色の輪は緑色の輪の上にあり、緑色の輪は青色の輪の上にあり、青色の輪は赤い色の輪の上にある。それゆえある輪をのぞけば残り2つの輪は分離可能である。同様に組みひもも2本のみを考えると上下関係があるが、3本では輪環の順となっている。
具現化
[編集]
分子で構築されたボロミアン環である分子ボロミアン環が存在する。この構造は機械的に分割不可能な形状である。1997年、生物学者のChengde Maoとニューヨーク大学の同僚はDNAから1組の輪を作り出すことに成功した[11]そして2003年、科学者のフレイザー・ストッダートとそのカリフォルニア大学ロサンゼルス校での同僚と錯体化学(配位化学)を用いて18個の部品から一度に輪を構成しようとしていた[10]金Au25(SR)18 やAgAg25(SR)18のようなチオラート配位子の表面層によって遮蔽されたある種の原子的に正確な貴金属クラスタの構造を表現するために、ボロミアン環構造が有効な方法であることを示した[12]。ハロゲン結合駆動自己集合によるジュゼッペ・レスナティと共同研究者らの設計により,Borromeanネットワークのライブラリを合成した。[13]
ボロミアン環の量子力学的類似体は1970年にそのような状態を予言したロシアの理論物理学者、ヴィタリ・エフィモフにちなんでエフィモフ状態と呼ばれている。オーストリアのインスブルック大学のInstitute for Experimental Physicsのルドルフ・グリムとハンス・クリストフ・ネーゲルの研究グループは、2006年、超低温のセシウムガス中でこの状態の実験的観察に初めて成功し、その結果を科学誌ネイチャーに発表した[14]。その後ヒューストンにあるライス大学のRandall Hulet教授が率いる物理学者チームは、結合したリチウム原子を3個集めてこれを実現し、その結果をオンライン雑誌Science Expressに発表した。[15] 2010年には、田中鐘信の率いるチームが炭素原子核内にエフィモフ状態を実現した。[16]
関連項目
[編集]注
[編集]参考文献
[編集]- ^ N. L. Biggs (1 March 1981). “T. P. Kirkman, Mathematician”. Bull. London Math. Soc. 13 (2): 116. doi:10.1112/blms/13.2.97 24 January 2017閲覧。.
- ^ Denis Vogel (13 February 2004), Massey products in the Galois cohomology of number fields, doi:10.11588/heidok.00004418, urn:nbn:de:bsz:16-opus-44188
- ^ Masanori Morishita (22 April 2009), Analogies between Knots and Primes, 3-Manifolds and Number Rings, arXiv:0904.3399, Bibcode: 2009arXiv0904.3399M
- ^ William Thurston (March 2002), “7. Computation of volume”, The Geometry and Topology of Three-Manifolds, p. 165
- ^ D.Wells 著、宮崎興二ら 訳『不思議おもしろ幾何学事典』朝倉書店、2002年、182頁。ISBN 978-4254110890。
- ^ ICM 2006
- ^ Arul Lakshminarayan (May 2007). “Borromean Triangles and Prime Knots in an Ancient Temple”. Indian Academy of Sciences. 18 September 2014閲覧。
- ^ Blog entry by Arul Lakshminarayan
- ^ Comments on Knives And Beer Bar Trick: Amazing Balance
- ^ a b Kelly S. Chichak; Stuart J. Cantrill; Anthony R. Pease; Sheng-Hsien Chiu; Gareth W. V. Cave; Jerry L. Atwood; J. Fraser Stoddart (28 May 2004). “Molecular Borromean Rings”. Science 304 (5675): 1308–1312. Bibcode: 2004Sci...304.1308C. doi:10.1126/science.1096914. PMID 15166376.
- ^ C. Mao; W. Sun; N. C. Seeman (1997). “Assembly of Borromean rings from DNA”. Nature 386 (6621): 137–138. Bibcode: 1997Natur.386..137M. doi:10.1038/386137b0. PMID 9062186.
- ^ Natarajan, Ganapati; Mathew, Ammu; Negishi, Yuichi; Whetten, Robert L.; Pradeep, Thalappil (2015-12-02). “A Unified Framework for Understanding the Structure and Modifications of Atomically Precise Monolayer Protected Gold Clusters” (英語). The Journal of Physical Chemistry C 119 (49): 27768–27785. doi:10.1021/acs.jpcc.5b08193. ISSN 1932-7447.
- ^ Vijith Kumar; Tullio Pilati; Giancarlo Terraneo; Franck Meyer; Pierangelo Metrangolo; Giuseppe Resnati (2017). “Halogen bonded Borromean networks by design: topology invariance and metric tuning in a library of multi-component systems”. Chemical Science 8 (3): 1801–1810. doi:10.1039/C6SC04478F. PMC 5477818. PMID 28694953.
- ^ T. Kraemer; M. Mark; P. Waldburger; J. G. Danzl; C. Chin; B. Engeser; A. D. Lange; K. Pilch et al. (2006). “Evidence for Efimov quantum states in an ultracold gas of caesium atoms”. Nature 440 (7082): 315–318. arXiv:cond-mat/0512394. Bibcode: 2006Natur.440..315K. doi:10.1038/nature04626. PMID 16541068.
- ^ Clara Moskowitz (December 16, 2009), Strange Physical Theory Proved After Nearly 40 Years, Live Science
- ^ K. Tanaka (2010), “Observation of a Large Reaction Cross Section in the Drip-Line Nucleus 22C”, Physical Review Letters 104 (6): 062701, Bibcode: 2010PhRvL.104f2701T, doi:10.1103/PhysRevLett.104.062701, PMID 20366816
関連文献
[編集]- P. R. Cromwell, E. Beltrami and M. Rampichini, "The Borromean Rings", Mathematical Intelligencer Vol. 20 no. 1 (1998) 53–62.
- Freedman, Michael H.; Skora, Richard (1987), “Strange Actions of Groups on Spheres”, Journal of Differential Geometry 25: 75–98, doi:10.4310/jdg/1214440725
- Lindström, Bernt; Zetterström, Hans-Olov (1991), “Borromean Circles are Impossible”, American Mathematical Monthly 98 (4): 340–341, doi:10.2307/2323803, JSTOR 2323803(subscription required). This article explains why Borromean links cannot be exactly circular.
- Brown, R. and Robinson, J., "Borromean circles", Letter, American Math. Monthly, April, (1992) 376–377. This article shows how Borromean squares exist, and have been made by John Robinson (sculptor), who has also given other forms of this structure.
- Chernoff, W. W., "Interwoven polygonal frames". (English summary) 15th British Combinatorial Conference (Stirling, 1995). Discrete Math. 167/168 (1997), 197–204. This article gives more general interwoven polygons.
- John Robinson, "Symbolic Sculptures and the Borromean Rings".
外部リンク
[編集]- "Borromean Rings Homepage", Dr Peter Cromwell's website.
- Jablan, Slavik. "Are Borromean Links So Rare?", Visual Mathematics.
- "Borromean rings", The Knot Atlas.
- "Borromean Rings", The Encyclopedia of Science.
- "Symbolic Sculpture and the Borromean Rings", Sculpture Maths.
- "African Borromean ring carving", Sculpture Maths.
- Borromean rings spinning as a group
- "The Borromean Rings: A new logo for the IMU" [w/video], International Mathematical Union
- Hunton, John. “Higher Linkages and Borromean Rings”. Numberphile. Brady Haran. 2013年5月24日時点のオリジナルよりアーカイブ。2013年4月6日閲覧。
