SHA-2
| 一般 | |
|---|---|
| 設計者 | アメリカ国家安全保障局 |
| 初版発行日 | 2001 |
| シリーズ | (SHA-0), SHA-1, SHA-2, SHA-3 |
| 認証 | FIPS PUB 180-4, CRYPTREC, NESSIE |
| 詳細 | |
| ダイジェスト長 | 224, 256, 384, or 512 bits |
| 構造 | Merkle-Damgård construction |
| ラウンド数 | 64 or 80 |
| 最良の暗号解読法 | |
| 2011年に原像攻撃によってSHA512の80ラウンド中57ラウンドまで、SHA-256の64ラウンド中52ラウンドまで[1]。疑似衝突攻撃ではSHA-256の46ラウンドまで[2]。 | |
SHA-2(シャーツー[3])は、Secure Hash Algorithmシリーズの暗号学的ハッシュ関数で、SHA-1の改良版である。アメリカ国家安全保障局によって設計され、2001年にアメリカ国立標準技術研究所によって連邦情報処理標準 PUB 180-4として標準化された。
概要[編集]
SHA-2には、前身のSHA-1から多くの改良が加えられている。それ以前のハッシュ関数は出力が固定長で強度もその長さによって決まる値に固定されていたが、SHA-2はSHA-224、SHA-256、SHA-384、SHA-512、SHA-512/224、SHA-512/256の6つのバリエーションを持ち、ハッシュ長は224、256、384、512ビットのいずれかである。
SHA-256とSHA-512は、それぞれ32ビット、64ビットのワード長から計算されるハッシュ関数である。シフト量と追加定数が異なるが、構造自体は本質的に同一であり、ラウンド数のみが異なる。SHA-224とSHA-384は、それぞれSHA-256とSHA-512を単純に切り詰めたバージョンであり、初期値のみが異なる。SHA-512/224とSHA-512/256は、SHA-256ではなくSHA-512を切り詰めたバージョンである。SHA-2シリーズは US 6829355 によってカバーされているが、アメリカ合衆国は、この特許をロイヤリティフリーで開放している[4]。
2004年にMD5とSHA-0の強衝突耐性が突破され[5]、翌2005年にはSHA-1の突破方法が発表された[6]。以降も攻撃法の研究が進む、といった事態が起きたため、急遽NIST主導で新たな構造を持つアルゴリズムのSHA-3の公募が2007年から5年かけて進められた[7][8]。公募後、3年の検証を経て、2015年8月にSHA-2の次のスタンダードとしてSHA-3が制定された[9]。SHA-2にはSHA-1と類似する点もあるものの、後述するように当時憂慮されたような事態にはなっていない(2015年6月現在)。
2014年1月現在、SHA-1に有効な攻撃をSHA-2に拡張することは達成されていない。原像攻撃ではSHA-256にて52ラウンドまで、SHA-512にて57ラウンドまで、衝突攻撃ではSHA-256の46ラウンドまでが最良の攻撃法である[1][2]。
SHA-2は、日本のCRYPTRECおよびヨーロッパのNESSIEにおいて、推奨暗号として採用されている。 [10]
ハッシュ関数の標準化[編集]
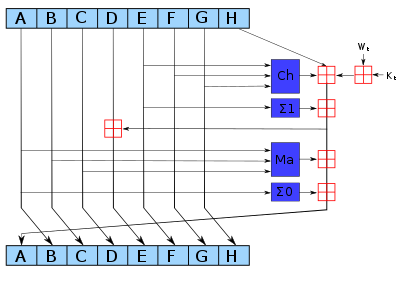
これらの値はSHA-256のものであり、SHA-512では異なる値が用いられる。
:addition modulo 232.
FIPS PUB 180-2において、3つのハッシュ関数がSHAシリーズに追加された。これらは出力されるハッシュ長のビット数からそれぞれSHA-256、SHA-384、SHA-512と呼ばれ、SHA-2と総称される。
アルゴリズムは2001年のFIPS PUB 180-2の草稿にて発表され、レビューやコメントが寄せられた。2002年8月、FIPS PUB 180-2は新たな標準 "Secure Hash Standard" として認定され、1995年に制定されたFIPS PUB 180-1を置き換えた。FIPS PUB 180-2には、180-1で規定されたSHA-1も含まれている[11]。
2004年2月、FIPS PUB 180-2のChange Noticeとして、鍵を2つ用いるトリプルDESの鍵長に合うように定義されたSHA-224が追加された[12]。2008年10月、FIPS PUB 180-3が制定されたが、これはSHA-224をChange Noticeから標準自体に取り込むほかには本質的な変化はなかった。この更新は、ハッシュ関数のセキュリティ情報の更新と、これらSHA-2をSpecial Publications 800-107および800-57において使用することを推奨するためのものであった[13][14][15]。詳細なテストデータとハッシュの例が標準から除去され、別文書とされた[16]。
2011年1月、NISTはSP800-131Aを発表した。これは、連邦政府組織におけるセキュリティ強度の下限について、それまでの80ビット(SHA-1によって得られる強度)の使用を2013年末までに限定し、それ以降は112ビット(SHA-224によって得られる強度)を下限とするものである[17]。
2012年3月、FIPS PUB 180-4が制定され、SHA-512を切り詰めたバージョンとしてSHA-512/224とSHA-512/256が追加された。また、入力データのパディングをハッシュ計算の前に行なうこととしていた制限が撤廃され、リアルタイムでの音声や映像などにおけるハッシュ計算をコンテンツ生成と同時に行うことが可能となった。最終ブロックのパディングのみは、引き続きハッシュ出力の前に行なうこととされている[18]。
2012年7月、NISTは暗号鍵管理に関するガイドラインであるSP800-57を改訂した。これは、2007年版において112ビット未満の電子署名の生成を2010年末までとしていたものを2013年までに変更するものである[15]。2012年8月にはSP800-107にも同様の変更がなされた[14]。
NISTは2012年に、かねてからコンペティションを進行させていたSHA-3の選出を行った[19]。コンペティションの趣旨により(詳細はSHA-3の記事などを参照)SHA-3はSHA-2(およびそれ以前の関数)とは類似しないものになっている。
用途[編集]
SHA-2ハッシュ関数は、TLS/SSL、OpenPGP、SSH、S/MIME、IPsec、Bitcoinといった広く使われているアプリケーションやプロトコルで利用されている。SHA-256は、Debian GNU/Linuxのソフトウェアパッケージの認証[20]や、DKIMにおけるメッセージ署名標準として利用されている。SHA-512は、ルワンダ国際戦犯法廷におけるビデオアーカイブの認証に用いられている[21]。SHA-256およびSHA-512は、DNSSECでの利用が提唱されている[22]。UnixやLinuxのベンダーでは、パスワードの安全なハッシュ法としてSHA-256やSHA-512への移行を始めている[23]。
SHA-1とSHA-2は、アメリカ合衆国において機密情報を扱う際に法律によって要求されるハッシュアルゴリズムの一つである。FIPS 180-1では、SHA-1を私的にあるいは商業で用いることも推奨している。SHA-1は合衆国政府での利用はほぼ終了しており、NISTでは「連邦組織は、電子署名、タイムスタンプ、衝突への耐性を必要とするアプリケーションでのSHA-1の利用を可及的速やかに中止すべきである。2010以降はSHA-2を利用すべきである」としている[24]。
SHA-2はセキュリティ的にSHA-1より優れているものの、SHA-1ほど広くは用いられていない。その理由として、Microsoft Windows XPのSP2以前がSHA-2をサポートしていないこと[25]や、SHA-1において実際の衝突が発見されていなかったために緊迫感に欠けたことが挙げられる。ただし後者については、2017年に2月23日にGoogleとオランダの研究機関CWI Instituteが共同で2つの異なるファイルから同じSHA-1ハッシュ値を生成する衝突に成功した。[26]
また、Windows XPのサポート終了などの背景から、公的機関でのSHA-1の使用を原則的に終了する動きがあり、民間のウェブサイトでもSHA-2へ移行するケースが出始めた(詳細はSHA-1#概要を参照)。
攻撃と認証[編集]
ハッシュ長が L ビットであるハッシュ関数において、与えられた特定のハッシュに対応する元のメッセージを見つけることは、総当たり攻撃では 2L の試行で可能である。これは原像攻撃と呼ばれる。一方、同じハッシュを与える2つの異なるメッセージを見つけることは衝突攻撃と呼ばれ、およそ 2L / 2 の試行で可能である。
SHA-3選定におけるハッシュ関数の解析への興味の増加によって、SHA-2への新しい攻撃が報告されている。最良の攻撃法を下のテーブルに示す。現時点では衝突攻撃のみが現実的な可能性を有しているが、フルバージョンのSHA-2に対する攻撃は成功していない。 Fast Software Encryption 2012において、ソニーの研究者によって、SHA-256で52ラウンドまで、SHA-512で57ラウンドまでbiclique疑似原像攻撃に基づく疑似衝突攻撃が可能であることが報告された[27]。
| 発表 | 発表年 | 攻撃法 | 攻撃 | 対象 | ラウンド数 | 試行 |
|---|---|---|---|---|---|---|
| New Collision attacks Against Up To 24-step SHA-2 [28] |
2008 | Deterministic | 衝突 | SHA-256 | 24/64 | 228.5 |
| SHA-512 | 24/80 | 232.5 | ||||
| Preimages for step-reduced SHA-2 [29] | 2009 | 中間一致 | 原像 | SHA-256 | 42/64 | 2251.7 |
| 43/64 | 2254.9 | |||||
| SHA-512 | 42/80 | 2502.3 | ||||
| 46/80 | 2511.5 | |||||
| Advanced meet-in-the-middle preimage attacks [30] |
2010 | 中間一致 | 原像 | SHA-256 | 42/64 | 2248.4 |
| SHA-512 | 42/80 | 2494.6 | ||||
| Higher-Order Differential Attack on Reduced SHA-256 [2] |
2011 | 差分解読 | 疑似衝突 | SHA-256 | 46/64 | 2178 |
| 46/64 | 246 | |||||
| Bicliques for Preimages: Attacks on Skein-512 and the SHA-2 family [1] |
2011 | Biclique | 原像 | SHA-256 | 45/64 | 2255.5 |
| SHA-512 | 50/80 | 2511.5 | ||||
| 疑似原像 | SHA-256 | 52/64 | 2255 | |||
| SHA-512 | 57/80 | 2511 |
公的認証[編集]
FIPSに認定されたすべての関数の実装は、NISTとCommunications Security Establishment Canada (CSEC)によるCryptographic Module Validation Programの認定を申請することが可能である。2013年現在、SHA-256については1300以上、SHA-512については900以上の実装が認定されている[31]。
ハッシュ値の例[編集]
空の入力に対するハッシュ値:
SHA224("") 0x d14a028c2a3a2bc9476102bb288234c415a2b01f828ea62ac5b3e42f SHA256("") 0x e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855 SHA384("") 0x 38b060a751ac96384cd9327eb1b1e36a21fdb71114be07434c0cc7bf63f6e1da274edebfe76f65fbd51ad2f14898b95b SHA512("") 0x cf83e1357eefb8bdf1542850d66d8007d620e4050b5715dc83f4a921d36ce9ce47d0d13c5d85f2b0ff8318d2877eec2f63b931bd47417a81a538327af927da3e SHA512/224("") 0x 6ed0dd02806fa89e25de060c19d3ac86cabb87d6a0ddd05c333b84f4 SHA512/256("") 0x c672b8d1ef56ed28ab87c3622c5114069bdd3ad7b8f9737498d0c01ecef0967a
入力メッセージのわずかな違いも、出力されるハッシュ値に大きな変化を及ぼす。例えば、メッセージの最後にピリオドを加えた場合:
SHA224("The quick brown fox jumps over the lazy dog") 0x 730e109bd7a8a32b1cb9d9a09aa2325d2430587ddbc0c38bad911525 SHA224("The quick brown fox jumps over the lazy dog.") 0x 619cba8e8e05826e9b8c519c0a5c68f4fb653e8a3d8aa04bb2c8cd4c
疑似コード[編集]
SHA-256アルゴリズムの疑似コードは以下の通りである。
Note 1: All variables are 32 bit unsigned integers and addition is calculated modulo 232 Note 2: For each round, there is one round constant k[i] and one entry in the message schedule array w[i], 0 ≤ i ≤ 63 Note 3: The compression function uses 8 working variables, a through h Note 4: Big-endian convention is used when expressing the constants in this pseudocode, and when parsing message block data from bytes to words, for example, the first word of the input message "abc" after padding is 0x61626380 Initialize hash values: (first 32 bits of the fractional parts of the square roots of the first 8 primes 2..19): h0 := 0x6a09e667 h1 := 0xbb67ae85 h2 := 0x3c6ef372 h3 := 0xa54ff53a h4 := 0x510e527f h5 := 0x9b05688c h6 := 0x1f83d9ab h7 := 0x5be0cd19 Initialize array of round constants: (first 32 bits of the fractional parts of the cube roots of the first 64 primes 2..311): k[0..63] := 0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5, 0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174, 0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da, 0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967, 0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85, 0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070, 0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3, 0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2 Pre-processing: append the bit '1' to the message append k bits '0', where k is the minimum number >= 0 such that the resulting message length (modulo 512 in bits) is 448. append length of message (without the '1' bit or padding), in bits, as 64-bit big-endian integer (this will make the entire post-processed length a multiple of 512 bits) Process the message in successive 512-bit chunks: break message into 512-bit chunks for each chunk create a 64-entry message schedule array w[0..63] of 32-bit words (The initial values in w[0..63] don't matter, so many implementations zero them here) copy chunk into first 16 words w[0..15] of the message schedule array Extend the first 16 words into the remaining 48 words w[16..63] of the message schedule array: for i from 16 to 63 s0 := (w[i-15] rightrotate 7) xor (w[i-15] rightrotate 18) xor (w[i-15] rightshift 3) s1 := (w[i-2] rightrotate 17) xor (w[i-2] rightrotate 19) xor (w[i-2] rightshift 10) w[i] := w[i-16] + s0 + w[i-7] + s1 Initialize working variables to current hash value: a := h0 b := h1 c := h2 d := h3 e := h4 f := h5 g := h6 h := h7 Compression function main loop: for i from 0 to 63 S1 := (e rightrotate 6) xor (e rightrotate 11) xor (e rightrotate 25) ch := (e and f) xor ((not e) and g) temp1 := h + S1 + ch + k[i] + w[i] S0 := (a rightrotate 2) xor (a rightrotate 13) xor (a rightrotate 22) maj := (a and b) xor (a and c) xor (b and c) temp2 := S0 + maj h := g g := f f := e e := d + temp1 d := c c := b b := a a := temp1 + temp2 Add the compressed chunk to the current hash value: h0 := h0 + a h1 := h1 + b h2 := h2 + c h3 := h3 + d h4 := h4 + e h5 := h5 + f h6 := h6 + g h7 := h7 + h Produce the final hash value (big-endian): digest := hash := h0 append h1 append h2 append h3 append h4 append h5 append h6 append h7
ch および maj の計算は、SHA-1と同様の手法により最適化できる。
SHA-224は本質的にSHA-256と同じであるが、以下の点が異なる。
- 初期値
h0からh7が異なる h7を除去することで出力が得られる
SHA-224 initial hash values (in big endian): (The second 32 bits of the fractional parts of the square roots of the 9th through 16th primes 23..53) h[0..7] := 0xc1059ed8, 0x367cd507, 0x3070dd17, 0xf70e5939, 0xffc00b31, 0x68581511, 0x64f98fa7, 0xbefa4fa4
SHA-512の構造は本質的にSHA-256と同じであるが、以下の点が異なる。
- メッセージが512ビットごとではなく1024ビットごとのチャンクに分けられる
- 初期値とラウンド定数が64ビットに拡張されている
- ラウンド数が64から80に変更されている
- メッセージ配列wは64個の32ビットワードではなく、80個の64ビットワードを持つ
- メッセージ配列wを拡張するためのループは16~63ではなく16~79
- ラウンド定数が最初の80個の素数 2..409 に基づいている
- 演算に用いられるワード長が64ビットである
- 末尾に追加されるメッセージ長が128ビットのビッグエンディアンである
- シフトとローテートの数が異なる
SHA-512 initial hash values (in big-endian): h[0..7] := 0x6a09e667f3bcc908, 0xbb67ae8584caa73b, 0x3c6ef372fe94f82b, 0xa54ff53a5f1d36f1, 0x510e527fade682d1, 0x9b05688c2b3e6c1f, 0x1f83d9abfb41bd6b, 0x5be0cd19137e2179 SHA-512 round constants: k[0..79] := [ 0x428a2f98d728ae22, 0x7137449123ef65cd, 0xb5c0fbcfec4d3b2f, 0xe9b5dba58189dbbc, 0x3956c25bf348b538, 0x59f111f1b605d019, 0x923f82a4af194f9b, 0xab1c5ed5da6d8118, 0xd807aa98a3030242, 0x12835b0145706fbe, 0x243185be4ee4b28c, 0x550c7dc3d5ffb4e2, 0x72be5d74f27b896f, 0x80deb1fe3b1696b1, 0x9bdc06a725c71235, 0xc19bf174cf692694, 0xe49b69c19ef14ad2, 0xefbe4786384f25e3, 0x0fc19dc68b8cd5b5, 0x240ca1cc77ac9c65, 0x2de92c6f592b0275, 0x4a7484aa6ea6e483, 0x5cb0a9dcbd41fbd4, 0x76f988da831153b5, 0x983e5152ee66dfab, 0xa831c66d2db43210, 0xb00327c898fb213f, 0xbf597fc7beef0ee4, 0xc6e00bf33da88fc2, 0xd5a79147930aa725, 0x06ca6351e003826f, 0x142929670a0e6e70, 0x27b70a8546d22ffc, 0x2e1b21385c26c926, 0x4d2c6dfc5ac42aed, 0x53380d139d95b3df, 0x650a73548baf63de, 0x766a0abb3c77b2a8, 0x81c2c92e47edaee6, 0x92722c851482353b, 0xa2bfe8a14cf10364, 0xa81a664bbc423001, 0xc24b8b70d0f89791, 0xc76c51a30654be30, 0xd192e819d6ef5218, 0xd69906245565a910, 0xf40e35855771202a, 0x106aa07032bbd1b8, 0x19a4c116b8d2d0c8, 0x1e376c085141ab53, 0x2748774cdf8eeb99, 0x34b0bcb5e19b48a8, 0x391c0cb3c5c95a63, 0x4ed8aa4ae3418acb, 0x5b9cca4f7763e373, 0x682e6ff3d6b2b8a3, 0x748f82ee5defb2fc, 0x78a5636f43172f60, 0x84c87814a1f0ab72, 0x8cc702081a6439ec, 0x90befffa23631e28, 0xa4506cebde82bde9, 0xbef9a3f7b2c67915, 0xc67178f2e372532b, 0xca273eceea26619c, 0xd186b8c721c0c207, 0xeada7dd6cde0eb1e, 0xf57d4f7fee6ed178, 0x06f067aa72176fba, 0x0a637dc5a2c898a6, 0x113f9804bef90dae, 0x1b710b35131c471b, 0x28db77f523047d84, 0x32caab7b40c72493, 0x3c9ebe0a15c9bebc, 0x431d67c49c100d4c, 0x4cc5d4becb3e42b6, 0x597f299cfc657e2a, 0x5fcb6fab3ad6faec, 0x6c44198c4a475817] SHA-512 Sum & Sigma: S0 := (a rightrotate 28) xor (a rightrotate 34) xor (a rightrotate 39) S1 := (e rightrotate 14) xor (e rightrotate 18) xor (e rightrotate 41) s0 := (w[i-15] rightrotate 1) xor (w[i-15] rightrotate 8) xor (w[i-15] rightshift 7) s1 := (w[i-2] rightrotate 19) xor (w[i-2] rightrotate 61) xor (w[i-2] rightshift 6)
SHA-384は本質的にSHA-512と同じであるが、以下の点が異なる。
- 初期値
h0からh7が異なる h6およびh7を除去することで出力が得られる
SHA-384 initial hash values (in big-endian):
h[0..7] := 0xcbbb9d5dc1059ed8, 0x629a292a367cd507, 0x9159015a3070dd17, 0x152fecd8f70e5939,
0x67332667ffc00b31, 0x8eb44a8768581511, 0xdb0c2e0d64f98fa7, 0x47b5481dbefa4fa4
SHA-512/tは本質的にSHA-512と同じであるが、以下の点が異なる。
- 初期値
h0からh7は SHA-512/t IV generation function によって与えられる h0からh7の t ビット目までで切り詰めることで出力が得られる- t が384となることは認められていない(SHA-384を使うべきである)
- t が224および256であるものが認定されている
SHAシリーズの比較[編集]
| アルゴリズムとバリエーション | 出力長 (bits) |
内部状態長 (bits) |
ブロック長 (bits) |
最大メッセージ長 (bits) |
ラウンド数 | ビット演算 | セキュリティ強度 (bits) |
パフォーマンスの例[33] (MiB/s) | |
|---|---|---|---|---|---|---|---|---|---|
| MD5 | 128 | 128 (4 × 32) |
512 | 264 − 1 | 64 | And, Xor, Rot, Add (mod 232), Or |
<64(強衝突) | 335 | |
| SHA-0 | 160 | 160 (5 × 32) |
512 | 264 − 1 | 80 | And, Xor, Rot, Add (mod 232), Or |
<80(強衝突) | - | |
| SHA-1 | 160 | 160 (5 × 32) |
512 | 264 − 1 | 80 | <63 (衝突発見[34]) |
192 | ||
| SHA-2 | SHA-224 SHA-256 |
224 256 |
256 (8 × 32) |
512 | 264 − 1 | 64 | And, Xor, Rot, Add (mod 232), Or, Shr |
112 128 |
139 |
| SHA-384 SHA-512 SHA-512/224 SHA-512/256 |
384 512 224 256 |
512 (8 × 64) |
1024 | 2128 − 1 | 80 | And, Xor, Rot, Add (mod 264), Or, Shr |
192 256 112 128 |
154 | |
| SHA-3 | SHA3-224 SHA3-256 SHA3-384 SHA3-512 |
224 256 384 512 |
1600 (5 × 5 × 64) |
1152 1088 832 576 |
制限なし[35] | 24[36] | And, Xor, Rot, Not |
112 128 192 256 |
- |
| SHAKE128 SHAKE256 |
d(可変長) d(可変長) |
1344 1088 |
d/2と128のいずれか小さい方 d/2と256のいずれか小さい方 |
- | |||||
| CPUアーキテクチャ | クロック周波数 | アルゴリズム | ワード長 (bits) | Cycles/Byte x86 | MiB/s x86 | Cycles/Byte x86-64 | MiB/s x86-64 |
|---|---|---|---|---|---|---|---|
| Intel Ivy Bridge | 3.5 GHz | SHA-256 | 32-bit | 16.80 | 199 | 13.05 | 256 |
| SHA-512 | 64-bit | 43.66 | 76 | 8.48 | 394 | ||
| AMD Piledriver | 3.8 GHz | SHA-256 | 32-bit | 22.87 | 158 | 18.47 | 196 |
| SHA-512 | 64-bit | 88.36 | 41 | 12.43 | 292 |
'x86' と表記されたパフォーマンス値は64ビットのプロセッサで32ビットのコードを実行したもの、'x86-64' と表記されたパフォーマンス値は64ビットのプロセッサで64ビットのコードを実行したものである。SHA-256は32ビット計算向けに設計されているが、64ビットプロセッサ向けの最適化の恩恵を受けている。SHA-512の32ビット環境での実装は、64ビット環境でのものと比較すると有意に遅くなっている。これら2つのアルゴリズムの変種(SHA-256ではSHA-224、SHA-512ではSHA-384、SHA-512/224、SHA-512/256)のパフォーマンスは、これらと同等である。MD5およびSHA-1の最適な実装の実効速度は4.5 - 6 Cycles/Byteである。このテストはイリノイ大学シカゴ校のhydra8システム(クロック周波数3.5 GHzのIntel Xeon E3-1275 V2)およびhydra9システム(クロック周波数3.8 GHzのAMD A10-5800K)によるものである[37][37][38]。
実装ライブラリ[編集]
SHA-2をサポートしているライブラリは以下の通り。
- Botan
- Bouncy Castle
- cryptlib
- Crypto++
- Libgcrypt
- Mbed TLS
- libsodium
- Nettle
- LibreSSL
- OpenSSL
- GnuTLS
- wolfSSL
脚注[編集]
- ^ a b c Dmitry Khovratovich, Christian Rechberger and Alexandra Savelieva (2011). “Bicliques for Preimages: Attacks on Skein-512 and the SHA-2 family”. IACR Cryptology ePrint Archive 2011:286.
- ^ a b c Mario Lamberger and Florian Mendel (2011). “Higher-Order Differential Attack on Reduced SHA-256”. IACR Cryptology ePrint Archive 2011:37.
- ^ “SHA2とは”. 2022年7月9日閲覧。
- ^ Licensing Declaration for US patent 6829355. 2008年2月17日閲覧。.
- ^ Collisions for Hash Functions MD4,MD5,HAVAL-128andRIPEMD 2022年4月28日閲覧。.
- ^ Finding Collisions in the Full SHA-1 2022年4月28日閲覧。.
- ^ “Federal Register / Vol. 72, No. 212” (PDF). Federal Register. Government Printing Office (2007年11月2日). 2022年4月24日閲覧。
- ^ “NIST Selects Winner of Secure Hash Algorithm (SHA-3) Competition”. NIST (2012年10月2日). 2012年10月2日閲覧。
- ^ NIST (August 2015). SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions. doi:10.6028/NIST.FIPS.202 2021年4月24日閲覧。.
- ^ “Announcing Approval of Federal Information Processing Standard (FIPS) 202, SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions, and Revision of the Applicability Clause of FIPS 180-4, Secure Hash Standard”. (2015年8月5日)
- ^ Federal Register Notice 02-21599, Announcing Approval of FIPS Publication 180-2
- ^ FIPS 180-2 with Change Notice 1
- ^ Federal Register Notice E8-24743, Announcing Approval of FIPS Publication 180-3
- ^ a b FIPS SP 800-107 Recommendation for Applications Using Approved Hash Algorithms
- ^ a b FIPS SP 800-57 Recommendation for Key Management: Part 1: General
- ^ NIST Algorithm Examples, Secure Hashing
- ^ FIPS SP 800-131A Recommendation for Transitioning the Use of Cryptographic Algorithms and Key Lengths
- ^ Federal Register Notice 2012-5400, Announcing Approval of FIPS Publication 180-4
- ^ NIST Selects Winner of Secure Hash Algorithm (SHA-3) Competition
- ^ “Debian codebase in Google Code”. Google. 2011年11月8日閲覧。[リンク切れ]
- ^ John Markoff, A Tool to Verify Digital Records, Even as Technology Shifts, New York Times, January 26, 2009
- ^ RFC 5702
- ^ Ulrich Drepper, Unix crypt with SHA-256/512
- ^ “NIST's March 2006 Policy on Hash Functions”. NIST (2006年3月15日). 2014年1月1日閲覧。
- ^ Microsoft Corporation,Overview of Windows XP Service Pack 3
- ^ https://security.googleblog.com/2017/02/announcing-first-sha1-collision.html
- ^ Ji Li, Takanori Isobe and Kyoji Shibutani, Sony China Research Laboratory and Sony Corporation, Converting Meet-in-the-Middle Preimage Attack into Pseudo Collision Attack: Application to SHA-2
- ^ Somitra Kumar Sanadhya and Palash Sarkar (2008). “New Collision attacks Against Up To 24-step SHA-2”. IACR Cryptology ePrint Archive 2008:270.
- ^ Kazumaro Aoki, Jian Guo, Krystian Matusiewicz, Yu Sasaki, and Lei Wang (2009). “Preimages for step-reduced SHA-2”. Advances in Cryptology - ASIACRYPT 2009. Lecture Notes in Computer Science (Springer Berlin Heidelberg) 5912: 578-597. doi:10.1007/978-3-642-10366-7_34. ISBN 978-3-642-10366-7. ISSN 0302-9743.
- ^ Jian Guo, San Ling, Christian Rechberger, and Huaxiong Wang (2010). “Advanced meet-in-the-middle preimage attacks: First results on full Tiger, and improved results on MD4 and SHA-2”. Advances in Cryptology - ASIACRYPT 2010. Lecture Notes in Computer Science (Springer Berlin Heidelberg) 6477: 56-75. doi:10.1007/978-3-642-17373-8_4. ISBN 978-3-642-17373-8. ISSN 0302-9743.
- ^ SHS Validation List
- ^ “Crypto++ 5.6.0 Benchmarks”. 2014年1月1日閲覧。
- ^ AMD Opteron 8354 2.2 GHzプロセッサと64ビット版Linuxによる計測[32]
- ^ “Announcing the first SHA1 collision”. 2017年2月23日閲覧。
- ^ “The Sponge Functions Corner”. 2016年1月28日閲覧。
- ^ “The Keccak sponge function family”. 2016年1月28日閲覧。
- ^ a b SUPERCOP Benchmarks Measurements of hash functions, indexed by machine
- ^ SUPERCOP Benchmarking Toolkit
参考文献[編集]
- Henri Gilbert, Helena Handschuh: Security Analysis of SHA-256 and Sisters. Selected Areas in Cryptography 2003: pp175–193
- “Proposed Revision of Federal Information Processing Standard (FIPS) 180, Secure Hash Standard”. Federal Register 59 (131): 35317–35318. (1994-07-11) 2007年4月26日閲覧。.
関連項目[編集]
外部リンク[編集]
- Descriptions of SHA-256, SHA-384, and SHA-512 from NIST
- Specifications for a Secure Hash Standard (SHS) – Draft for proposed SHS (SHA-0)
- Secure Hash Standard (SHS) – Proposed SHS (SHA-0)
- CSRC Cryptographic Toolkit – Official NIST site for the Secure Hash Standard
- FIPS 180-4: Secure Hash Standard (SHS) (PDF, 1.7 MB) – Current version of the Secure Hash Standard (SHA-1, SHA-224, SHA-256, SHA-384, and SHA-512), March 2012
- Test vectors for SHA-256/384/512 from the NESSIE project
- Test vectors for SHA-1, SHA-2 from NIST site
- NIST Cryptographic Hash Project SHA-3 competition
- RFC 3874: A 224-bit One-way Hash Function: SHA-224.
- RFC 6234: US Secure Hash Algorithms SHA and SHA-based HMAC and HKDF. Contains sample C implementation.
- SHA-2のSSLサーバ証明書のテストサイト(シマンテック)





