暗号利用モード
暗号利用モード(あんごうりようモード、Block cipher modes of operation)とは、ブロック暗号を利用して、ブロック長よりも長いメッセージを暗号化するメカニズムのことである。
ECBモード(単純なブロック暗号の利用法)では、ある鍵で同一の平文を暗号化すると、同一の暗号文になる。したがって、長いメッセージ(画像データなど)のある部分が他の部分と同じであるかどうかが、暗号文の比較によって判断できてしまうので、他のモードが必要となった。
暗号利用モードには、秘匿用の利用モードと、認証用の利用モードとがある。
秘匿用の利用モード[編集]
秘匿用として多くの暗号利用モードが定義されており、これらのうち、ECB, CBC, OFB, CFBの4つは、FIPS, ANSIのほか、ISO、JISで規格化されている。またCTRは、AES制定の際に追加されたモードである。
代表的な暗号利用モードを以下に示す。以下の説明で、 は暗号化後のi番目のブロック、は暗号化前のi番目のブロック、はブロック暗号処理を表す。
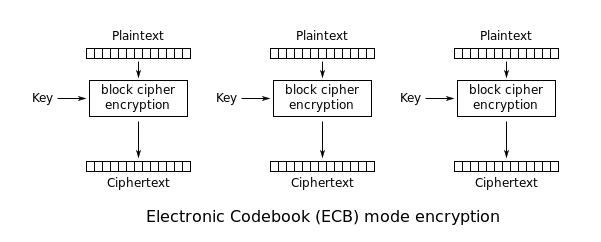
Electronic Codebook (ECB)[編集]
| ECB | |
|---|---|
| Electronic Codebook | |
| 暗号化処理の並列化: | 可 |
| 復号処理の並列化: | 可 |
| Random Read: | 可 |
ECBモード (Electronic Codebook Mode) は、もっとも単純な暗号利用モードである。メッセージはブロックに分割され、それぞれのブロックは独立して暗号化される。
ECBモードの欠点は、同じ鍵を用いた場合には、同じ平文ブロックを暗号化した結果の暗号文ブロックが常に同じとなることである。このため、データのパターンを隠蔽することができない。メッセージの機密性の保持には向かず、暗号化プロトコルにおける使用は推奨されない。同じ入力に対して常に同じ出力を返すことから、ECBモードは反射攻撃に対しても脆弱である。
ECBモードにおいてデータのパターンがどの程度残されるかを、ビットマップ画像の暗号化を用いて説明する。各々のピクセルの色情報を暗号化しても、暗号化処理後の画像にはピクセルごとの色情報のパターンが残留している。
Cipher Block Chaining (CBC)[編集]
| CBC | |
|---|---|
| Cipher Block Chaining | |
| 暗号化処理の並列化: | 不可 |
| 復号処理の並列化: | 可 |
| Random Read: | 可 |
CBCモード (Cipher Block Chaining Mode) は、1976年にIBMによって開発された[1]。CBCモードでは、平文の各ブロックは前の暗号文とのXORを取ってから暗号化される。すなわち、各々の暗号文ブロックはそれ以前のすべての平文ブロックに依存することとなる。メッセージごとのユニーク性を確保するため、最初のブロックの暗号化には初期化ベクトルが用いられる。
- 暗号化
- 復号
CBCモードは、最も広く用いられている暗号利用モードであり、ECBモードの欠点を補うものである。このモードの主な欠点は、各ブロックの暗号化にその前のブロックの暗号化の結果を使用することから暗号化処理を並列化することができないことと、暗号文ブロックのサイズの整数倍となるようメッセージをパディングする必要があることである。後者の例の一つが、Ciphertext stealingと呼ばれるものである。CBCモードの暗号化においては、平文あるいは初期化ベクトルが1ビットでも変化すると、それ以降の暗号文すべてが変化することとなる。
不正な初期化ベクトルを用いて復号した場合、復号後の平文の最初のブロックは正しい結果とはならないが、それ以降のブロックは正しく復号される。これは、隣接する2つの暗号文ブロックから平文を回復することが可能なためである。これにより、CBCモードの復号処理は並列化が可能となる。CBCモードの復号においては、暗号文が1ビット変化した場合、その位置に対応するブロック全体および次のブロックにおける対応するビットの復号結果に影響を及ぼすが、それ以外のブロックには影響を及ぼさない。
Propagating Cipher Block Chaining (PCBC)[編集]
| PCBC | |
|---|---|
| Propagating Cipher Block Chaining | |
| 暗号化処理の並列化: | 不可 |
| 復号処理の並列化: | 不可 |
| Random Read: | 不可 |
PCBCモード (Propagating Cipher Block Chaining Mode[2] あるいは Plaintext Cipher Block Chaining mode[3]) は、CBCモードの変法である。
- 暗号化
- 復号
PCBCモードはケルベロス認証のバージョン4およびWASTEにおいて用いられているが、あまり一般的ではない。PCBCモードでは隣接する2つの暗号文ブロックを入れ替えたとしてもそれ以降のブロックの復号に影響しない[4]。このため、ケルベロス認証のバージョン5ではPCBCモードは採用されていない。
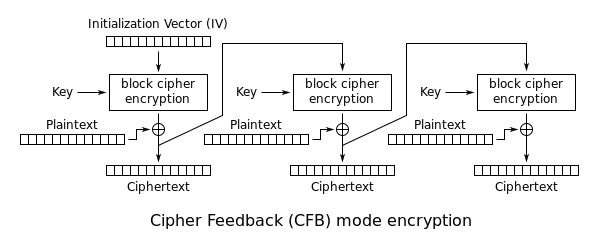
Cipher Feedback (CFB)[編集]
| CFB | |
|---|---|
| Cipher Feedback | |
| 暗号化処理の並列化: | 不可 |
| 復号処理の並列化: | 可 |
| Random Read: | 可 |
CFBモード (Cipher Feedback Mode) は、CBCモードと類似しており、ブロック暗号を自己同期型のストリーム暗号として扱うものである。CFBモードの操作はCBCモードとよく似ており、特に復号処理はCBCモードでの復号処理をほぼそのまま逆転させたものとなる。
- 暗号化
- 復号
上に示したもっとも単純なCFBモードでは、CBCモードのような自己同期型とはなっていない。1バイト、1ビットでも欠けた場合にはそれ以降の復号は不可能となる。そのような欠落の後も同期を続けるためには、1バイト、1ビットを同時に暗号化する必要がある。ブロック暗号の入力にシフトレジスタを組み合わせることで、CFBモードは自己同期型で利用することが可能となる。
CFBモードを任意のxの整数倍の欠落に対しても同期を維持することが可能な自己同期型のストリーム暗号として利用するためには、ブロックサイズと初期化ベクトルのサイズでシフトレジスタを初期化する必要がある。これはブロック暗号によって暗号化され、暗号化結果の上位xビットは平文のxビットとのXORを取られ、これがxビットの暗号文となる。これらxビットの出力はシフトレジスタにシフトされ、次のxビットの平文の処理に用いられる。復号も同様であり、初期化ベクトルから始まり、復号、復号結果の上位xビットと暗号文のxビットのXORによりxビットの平文となり、これが次のxビットの暗号文の処理に用いられる。このような処理はCFB-8あるいはCFB-1として知られている(シフト量の大きさによる)[5]。
まとめると次のようになる。ここで、Si は i 番目のシフトレジスタの状態、a << x は x ビットだけシフトした a、head(a, x) は a の上位 x ビット、n は初期化ベクトルのビット数である。
- 暗号化
- 復号
- 凡例
暗号文からxビットが失われた場合、シフトレジスタによって再度同期されるまでは復号結果は正しいものとはならない。すなわち、平文の欠落は最大でも1ブロック分に留まることとなる。
CBCモードと同様に、平文における1ビットの変化であっても暗号文全体に及ぶため、暗号化処理の並列化は不可能である。同様に、復号処理の並列化は可能である。
CFBモードは、OFBモードやCTRモードと同様、CBCモードと比較して2つの利点を有している。ブロック暗号を暗号化処理にのみ用いることと、ブロックサイズの整数倍にメッセージのパディングを行う必要がないことである。
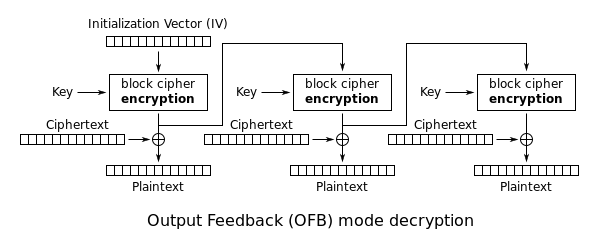
Output Feedback (OFB)[編集]
| OFB | |
|---|---|
| Output Feedback | |
| 暗号化処理の並列化: | 不可 |
| 復号処理の並列化: | 不可 |
| Random Read: | 不可 |
OFBモード (Output Feedback Mode) は、ブロック暗号を同期型のストリーム暗号として扱うものである。OFBモードでは、鍵ストリームを生成し、これと平文ブロックのXORを取ることで暗号文を得る。他のストリーム暗号と同様に、暗号文のビットをフリップさせると、平文の対応するビットがフリップする。この性質により、暗号化の前であっても前方誤り補正を適用することが可能となる。
XOR操作の対称性により、暗号化と復号は全く同じ操作となる。
- 暗号化
- 復号
- 凡例
各々の操作はそれ以前のすべての操作に依存していることから、暗号化、復号ともに処理の並列化は不可能である。しかし、平文あるいは暗号文は各操作の最後のXORにのみ用いられることから、ブロック暗号による操作を先行して処理しておき、XORのみを最後に連続して行うことは可能である。
入力として0が連続する文字列を定数としてCBCモードを使用することでOFBモードの鍵ストリームを生成することができる。これは、CBCモード向けの高速なハードウェア実装をOFBモードに流用することが可能であることを意味する。
CFBモードのようにブロックの一部をフィードバックに用いた場合、OFBモードにおける平均サイクル長はあるいはそれ以上小さくなる。Davies、Parkinによる数学モデルと、実験による検証から、完全なフィードバックの場合にのみサイクル長は最大となることが明らかとなった。このため、OFBモードの仕様からフィードバックの切り詰めのサポートは除去されている[6][7]。
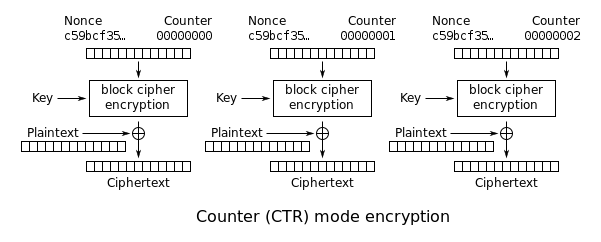
Counter (CTR)[編集]
| CTR | |
|---|---|
| Counter | |
| 暗号化処理の並列化: | 可 |
| 復号処理の並列化: | 可 |
| Random Read: | 可 |
CTRモード (Counter Mode) は、ブロック暗号を同期型のストリーム暗号として扱うものである。integer counter mode (ICM) あるいは segmented integer counter mode (SIC) とも呼ばれる。
「カウンター」と呼ばれる値を暗号化することで鍵ストリームブロックを生成する。カウンターとしては、単調増加であり値が重複することがなければどのような関数でも用いることができるが、1ずつ増加するものがもっとも単純でありもっとも一般的である。単純かつ決定論的な関数をカウンターとして用いることには異論があり、批評家は「暗号システムを系統だった入力に晒すことは、不必要なリスクを招くものである」と主張していた[8]。現在では、CTRモードは広く受け入れられており、入力関数に由来する問題はCTRモードではなく基礎となるブロック暗号によるものと認識されている[9]。CTRモードはNiels FergusonおよびBruce Schneierによって推薦される2つの暗号利用モードのうちの1つとなっている(もう1つはCBCモード)[10]。
CTRモードはOFBモードに似た性質を示すが、復号におけるランダムアクセス性を有している。CTRモードは暗号化、復号のいずれも並列処理が可能であり、マルチプロセッサ環境に適している。また、OFBモードのような短いサイクルの問題も存在しない[11]。
下記のダイアグラムにおけるNonceは、他の暗号利用モードにおける初期化ベクトルに相当する。Nonceとカウンターを無損失操作(連結、add、XOR)によって組み合わせることで、実際に用いられるカウンターブロックが生成される。
その他[編集]
- CTS (Ciphertext stealing)
- 2DEM (2D Encryption Mode)
- ABC (Accumulated Block Chaining)
- IGE (Infinite Garble Extension)
- F8@3GPP , ,
など
認証用の利用モード[編集]
認証用の利用モードとして次のものなどが知られている。
- CCM (Counter with CBC-MAC)
- GCM (Galois/Counter Mode)
- OCB (Offset CodeBook)
- XCBC (eXtended Ciphertext Block Chaining)
- XCBC-MAC
規格[編集]
- FIPS PUB-81 DES MODES OF OPERATION, 1980 December 2.
- ANSI X3.106 Digital encryption Algorithm - Modes of Operation
- ISO 8372:1987 Information processing -- Modes of operation for a 64-bit block cipher algorithm
- ISO/IEC 10116 Information technology -- Security techniques -- Modes of operation for an n-bit block cipher
- JIS X 5052:1990 64ビットのブロック暗号アルゴリズムの利用モード (Modes of operation for a 64-bit block cipher algorithm)
- JIS X 5053:1998 セキュリティ技術 ― nビットブロック暗号の利用モード (Information technology -- Security techniques -- Modes of operation for an n-bit block cipher)
- RFC 3610 -- Counter with CBC-MAC (CCM)
脚注[編集]
- ^ William F. Ehrsam, Carl H. W. Meyer, John L. Smith, Walter L. Tuchman, "Message verification and transmission error detection by block chaining", US Patent 4074066, 1976
- ^ http://www.iks-jena.de/mitarb/lutz/security/cryptfaq/q84.html
- ^ Kaufman, C.; Perlman, R.; Speciner, M. (2002). Network Security (2nd ed.). Upper Saddle River, NJ: Prentice Hall. p. 319. ISBN 0130460192
- ^ Kohl, J. (1990). “The Use of Encryption in Kerberos for Network Authentication”. Proceedings, Crypto '89. Berlin: Springer. ISBN 0387973176. オリジナルの2009年6月12日時点におけるアーカイブ。
- ^ NIST: Recommendation for Block Cipher Modes of Operation
- ^ Davies, D. W.; Parkin, G. I. P. (1983). “The average cycle size of the key stream in output feedback encipherment”. Advances in Cryptology, Proceedings of CRYPTO 82. New York: Plenum Press. pp. 263–282. ISBN 0306413663
- ^ http://www.crypto.rub.de/its_seminar_ws0809.html[リンク切れ]
- ^ Jueneman, Robert R. (1983). “Analysis of certain aspects of output feedback mode”. Advances in Cryptology, Proceedings of CRYPTO 82. New York: Plenum Press. pp. 99–127. ISBN 0306413663
- ^ Helger Lipmaa, Phillip Rogaway, and David Wagner. Comments to NIST concerning AES modes of operation: CTR-mode encryption. 2000
- ^ Niels Ferguson, Bruce Schneier, Tadayoshi Kohno, Cryptography Engineering, page 71, 2010
- ^ http://www.quadibloc.com/crypto/co040601.htm