複素平面内のクラインの j -不変量 数学では複素変数 τ の函数であるフェリックス・クライン の j -不変量j -invariant)(もしくはj -函数上半平面 上に定義された SL(2, Z ) のウェイト 0 のモジュラー函数 である。j -不変量として、尖点 で一位の極を持つ以外は正則な関数であり、次を満たすものが一意に定まる。
j
(
e
2
3
π
i
)
=
0
,
j
(
i
)
=
1728
{\displaystyle j\left(e^{{\frac {2}{3}}\pi i}\right)=0,\quad j(i)=1728}
j の有理函数はモジュラーであり、実際にすべてのモジュラー函数を与える。古典的には、j -不変量は C 楕円曲線 のパラメータ化として研究されていたが、驚くべきことに、モンスター群 の対称性との関係を持っている(この関係はモンストラス・ムーンシャイン と呼ばれる)。
j -不変量はある無限和(下記の g 2 , g 3 を参照)で純粋に定義することができるが、これらは楕円曲線の同型類を考えることが動機となる。C 上のすべての楕円曲線 E は複素トーラスであるので、ランク 2 の格子、つまり C の 2 次元格子と同一視できる。格子の互いに平行な反対側の辺を同一視することで、そのようにみなすことができる。複素数を格子に掛けることは格子の回転やスケーリングに対応し、これらは楕円曲線の同型類を保存することがわかり、このことから、格子を 1 と上半平面 H のある元 τ によって生成されると考えてよい。逆に、
g
2
=
60
∑
(
m
,
n
)
≠
(
0
,
0
)
(
m
+
n
τ
)
−
4
,
{\displaystyle g_{2}=60\sum _{(m,n)\neq (0,0)}(m+n\tau )^{-4},}
g
3
=
140
∑
(
m
,
n
)
≠
(
0
,
0
)
(
m
+
n
τ
)
−
6
,
{\displaystyle g_{3}=140\sum _{(m,n)\neq (0,0)}(m+n\tau )^{-6},}
と定義すると、この格子はヴァイエルシュトラスの楕円函数 を通して、y2 = 4x3 − g2 x - g3 で定義された C 上の楕円曲線に対応する。このとき、j -不変量は、
j
(
τ
)
=
1728
g
2
3
Δ
{\displaystyle j(\tau )=1728\,{\frac {g_{2}^{3}}{\Delta }}}
と定義される。ここにモジュラー判別式 (modular discriminant) Δ は
Δ
=
g
2
3
−
27
g
3
2
{\displaystyle \Delta =g_{2}^{3}-27g_{3}^{2}}
である。
Δ はウェイト 12 のモジュラー形式 であることと、g 2 はウェイト 4 のモジュラー形式であるのでその3乗はウェイト 12 であることを示すことができる。したがって、 j がこれらの商であることから j はウェイト 0 のモジュラ函数であり、特に、SL(2, Z ) の作用の下に不変な有理型函数 H → C である。以下に説明するように j は全射であり、このことは C 上の楕円曲線の同型類と複素数の間の全単射を与えることを意味する。
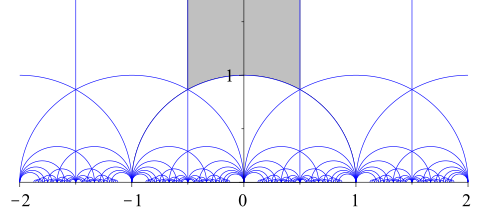
上半平面上に作用するモジュラ群の基本領域 2つの変換 τ → τ + 1 と τ → -τ−1 はモジュラ群 と呼ばれる群 を生成し、この群は射影特殊線型群 PSL(2, Z ) と同一視できる。この群に属する適当な変換
τ
↦
a
τ
+
b
c
τ
+
d
,
a
d
−
b
c
=
1
,
{\displaystyle \tau \mapsto {\frac {a\tau +b}{c\tau +d}},\qquad ad-bc=1,}
を選択することにより、τ を j の基本領域 (英語版 ) j に対して同じ値をとる、ある値に帰着させることができる。基本領域は次の条件を満たす τ から構成されている。
|
τ
|
≥
1
−
1
2
<
R
(
τ
)
≤
1
2
−
1
2
<
R
(
τ
)
<
0
⇒
|
τ
|
>
1
.
{\displaystyle {\begin{aligned}|\tau |&\geq 1\\-{\tfrac {1}{2}}&<{\mathfrak {R}}(\tau )\leq {\tfrac {1}{2}}\\-{\tfrac {1}{2}}&<{\mathfrak {R}}(\tau )<0\Rightarrow |\tau |>1\end{aligned}}.}
函数 j (τ) をこの領域へ制限すると、複素数 C のすべての値をちょうど一度だけ取る。言い換えると、C すべての元 c に対し、c = j (τ) となる基本領域の元 τ が一意に存在する。このように、j は基本領域を全複素平面へ写像するという性質を持っている。
リーマン面として、基本領域の種数は 0 であり、すべての(レベル 1 の)モジュラー函数は j の有理函数 であり、逆に、j のすべての有理函数はモジュラー函数である。言い換えると、モジュラー函数全体のなす体は C (j ) である。
j -不変量は、多くの注目すべき性質を有する。
τ が虚数乗法 である、すなわち、虚数部が正である虚二次体 の任意の元である(従って、j-不変量が定義される)ならば、j (τ) は代数的整数 である[ 1] 体の拡大 Q [j (τ), τ]/Q (τ)ガロア群 がアーベル的になる。 Λ を {1, τ} で生成される C の中の格子とすると、乗法の下に Λ を固定する Q (τ) のすべての元が、整環 (英語版 ) Q (τ) 上で j (τ) の代数的共役 である j (τ') を定義する。包含関係に従い、Q (τ) の唯一の最大整環は、Q (τ) の代数的整数の環であり、その環を持つ τ の値は、Q (τ) の不分岐拡大 を導く。 これらの古典的な結果は、虚数乗法 論の出発点となっている。
1937年、テオドール・シュナイダー (英語版 ) j (τ) は代数的数であるということを証明した。加えて、 τ が代数的数 だが虚二次体の数でないならば、j (τ) は超越数であることをも証明した。
j -函数は数多くの超越的性質を持つ。クルト・マーラー (英語版 ) j (τ) は双方が同時に代数的にはならないであろうという予想である。現在はより強い結果が知られていて、例えば、exp(2πiτ) が代数的であれば次の 3つの数は代数的に独立で、超越数になる。
j
(
τ
)
,
j
′
(
τ
)
π
,
j
′
′
(
τ
)
π
2
.
{\displaystyle j(\tau ),{\frac {j^{\prime }(\tau )}{\pi }},{\frac {j^{\prime \prime }(\tau )}{\pi ^{2}}}.}
j の注目すべき性質のいくつかは、q = exp(2πiτ) でのローラン級数 として書かれるq-展開 (フーリエ級数 展開)に関連している。q -展開は、
j
(
τ
)
=
1
q
+
744
+
196884
q
+
21493760
q
2
+
864299970
q
3
+
20245856256
q
4
+
⋯
{\displaystyle j(\tau )={1 \over q}+744+196884q+21493760q^{2}+864299970q^{3}+20245856256q^{4}+\cdots }
で始まっている。
なお、 j は尖点で一位の単純極 を持つので、q-展開には q−1 未満の項がない。
このフーリエ係数はすべて整数であり、このことがいくつかの概整数 、例えば有名なラマヌジャン定数 (英語版 )
e
π
163
≈
640320
3
+
744
{\displaystyle e^{\pi {\sqrt {163}}}\approx 640320^{3}+744}
qn の係数の漸近公式 (英語版 ) ハーディ・リトルウッドの円周法 (英語版 )
e
4
π
n
2
n
3
/
4
{\displaystyle {\frac {e^{4\pi {\sqrt {n}}}}{{\sqrt {2}}n^{3/4}}}}
により与えられる。[ 2] [ 3]
さらに注目すべきは、q の正のべき乗の項のフーリエ係数がムーンシャイン加群 (英語版 ) モンスター群 の無限次元次数付き代数 表現の次数部の次元であることである。特に、qn の係数は、ムーシャイン加群の次数 n の次元となっている。第一の例はグライス代数 (英語版 ) ムーンシャイン理論 の出発点であった。
ムーンシャイン予想の研究は、ジョン・ホートン・コンウェイ とシモン・ノートン (英語版 ) ジョン・G・トンプソン は、
q
−
1
+
O
(
q
)
{\displaystyle q^{-1}+{O}(q)}
という形式に正規化される種数 0 のモジュラ函数が、有限個しか存在しないことを証明した。
λ をモジュララムダ函数 (英語版 )
j
(
τ
)
=
256
(
1
−
x
)
3
x
2
{\displaystyle j(\tau )={\frac {256(1-x)^{3}}{x^{2}}}}
を得る。
λ
(
τ
)
=
θ
2
4
(
0
,
τ
)
θ
3
4
(
0
,
τ
)
=
k
2
(
τ
)
{\displaystyle \lambda (\tau )={\frac {\theta _{2}^{4}(0,\tau )}{\theta _{3}^{4}(0,\tau )}}=k^{2}(\tau )}
は、ヤコビのテータ函数
θ
m
{\displaystyle \theta _{m}}
k
(
τ
)
{\displaystyle k(\tau )}
[ 4] 非調和比 (cross-ratio)の 6つの値で入れ替わるときは、j の値は不変である[ 5]
{
λ
,
1
1
−
λ
,
λ
−
1
λ
,
1
λ
,
λ
λ
−
1
,
1
−
λ
}
.
{\displaystyle \left\lbrace {\lambda ,{\frac {1}{1-\lambda }},{\frac {\lambda -1}{\lambda }},{\frac {1}{\lambda }},{\frac {\lambda }{\lambda -1}},1-\lambda }\right\rbrace .}
j の分岐点は {0, 1, ∞} であるので、ベリイ函数 (英語版 ) [ 6]
q
=
e
π
i
τ
{\displaystyle q=e^{\pi i\tau }}
ノーム )と定義し直すと、ヤコビのテータ函数
ϑ
(
0
;
τ
)
=
ϑ
00
(
0
;
τ
)
=
1
+
2
∑
n
=
1
∞
(
e
π
i
τ
)
n
2
=
∑
n
=
−
∞
∞
q
n
2
{\displaystyle \vartheta (0;\tau )=\vartheta _{00}(0;\tau )=1+2\sum _{n=1}^{\infty }\left(e^{\pi i\tau }\right)^{n^{2}}=\sum _{n=-\infty }^{\infty }q^{n^{2}}}
から指標付きテータ函数 を導くことができる。次のように置くこととする。
a
=
θ
2
(
0
;
q
)
=
ϑ
10
(
0
;
τ
)
{\displaystyle a=\theta _{2}(0;q)=\vartheta _{10}(0;\tau )}
b
=
θ
3
(
0
;
q
)
=
ϑ
00
(
0
;
τ
)
{\displaystyle b=\theta _{3}(0;q)=\vartheta _{00}(0;\tau )}
c
=
θ
4
(
0
;
q
)
=
ϑ
01
(
0
;
τ
)
{\displaystyle c=\theta _{4}(0;q)=\vartheta _{01}(0;\tau )}
ここに
θ
m
{\displaystyle \theta _{m}}
ϑ
n
{\displaystyle \vartheta _{n}}
ヴァイエルシュトラス定数 g2 , g3 とデデキントのエータ函数 η(τ) に対して、
g
2
(
τ
)
=
2
3
π
4
(
a
8
+
b
8
+
c
8
)
{\displaystyle g_{2}(\tau )={\tfrac {2}{3}}\pi ^{4}\left(a^{8}+b^{8}+c^{8}\right)}
g
3
(
τ
)
=
4
27
π
6
(
a
8
+
b
8
+
c
8
)
3
−
54
(
a
b
c
)
8
2
{\displaystyle g_{3}(\tau )={\tfrac {4}{27}}\pi ^{6}{\sqrt {\frac {(a^{8}+b^{8}+c^{8})^{3}-54(abc)^{8}}{2}}}}
Δ
=
g
2
3
−
27
g
3
2
=
(
2
π
)
12
η
(
τ
)
24
=
(
2
π
)
12
(
1
2
a
b
c
)
8
{\displaystyle \Delta =g_{2}^{3}-27g_{3}^{2}=(2\pi )^{12}\eta (\tau )^{24}=(2\pi )^{12}\left({\tfrac {1}{2}}abc\right)^{8}}
となる。このようにすると、j (τ) を早く計算できる形に書き換えることができる。
j
(
τ
)
=
1728
g
2
3
g
2
3
−
27
g
3
2
=
32
(
a
8
+
b
8
+
c
8
)
3
(
a
b
c
)
8
.
{\displaystyle j(\tau )=1728{\frac {g_{2}^{3}}{g_{2}^{3}-27g_{3}^{2}}}=32{(a^{8}+b^{8}+c^{8})^{3} \over (abc)^{8}}.}
ただし、
a
4
−
b
4
+
c
4
=
0
{\displaystyle a^{4}-b^{4}+c^{4}=0}
であることに注意する。
今までは、j を複素変数の函数として考えてきたが、楕円曲線の同型類の不変量としては、j を純粋に代数的に定義することもできる。
y
2
+
a
1
x
y
+
a
3
y
=
x
3
+
a
2
x
2
+
a
4
x
+
a
6
{\displaystyle y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}}
を任意の体の上の平面楕円曲線とすると、
b
2
=
a
1
2
+
4
a
2
,
b
4
=
a
1
a
3
+
2
a
4
{\displaystyle b_{2}=a_{1}^{2}+4a_{2},\quad b_{4}=a_{1}a_{3}+2a_{4}}
b
6
=
a
3
2
+
4
a
6
,
b
8
=
a
1
2
a
6
−
a
1
a
3
a
4
+
a
2
a
3
2
+
4
a
2
a
6
−
a
4
2
{\displaystyle b_{6}=a_{3}^{2}+4a_{6},\quad b_{8}=a_{1}^{2}a_{6}-a_{1}a_{3}a_{4}+a_{2}a_{3}^{2}+4a_{2}a_{6}-a_{4}^{2}}
c
4
=
b
2
2
−
24
b
4
,
c
6
=
−
b
2
3
+
36
b
2
b
4
−
216
b
6
{\displaystyle c_{4}=b_{2}^{2}-24b_{4},\quad c_{6}=-b_{2}^{3}+36b_{2}b_{4}-216b_{6}}
と定義することができ、
Δ
=
−
b
2
2
b
8
+
9
b
2
b
4
b
6
−
8
b
4
3
−
27
b
6
2
{\displaystyle \Delta =-b_{2}^{2}b_{8}+9b_{2}b_{4}b_{6}-8b_{4}^{3}-27b_{6}^{2}}
と表すと、これは楕円曲線の判別式 を表している。
ここで、楕円曲線の j-不変量を
j
=
c
4
3
Δ
{\displaystyle j={c_{4}^{3} \over \Delta }}
と定義する。
楕円曲線が定義されている体の標数が 2 もしくは 3 でない場合に、この定義は
j
=
1728
c
4
3
c
4
3
−
c
6
2
{\displaystyle j=1728{c_{4}^{3} \over c_{4}^{3}-c_{6}^{2}}}
と書き直すことができる。
j-不変量の逆函数 は、超幾何函数 2 F1 で表すこともできる(ピカール・フックス方程式 (英語版 )
方法 1 : モジュララムダ函数 (英語版 )
j
(
τ
)
=
256
(
1
−
λ
(
1
−
λ
)
)
3
(
λ
(
1
−
λ
)
)
2
.
{\displaystyle j(\tau )={\frac {256(1-\lambda (1-\lambda ))^{3}}{(\lambda (1-\lambda ))^{2}}}.}
x = λ(1−λ) とすると 6次式は x の 3次式となる。すると、λ の 6つの値のどれに対しても、
τ
=
i
2
F
1
(
1
2
,
1
2
,
1
,
1
−
λ
)
2
F
1
(
1
2
,
1
2
,
1
,
λ
)
{\displaystyle \tau =i\ {\frac {{}_{2}F_{1}\left({\tfrac {1}{2}},{\tfrac {1}{2}},1,1-\lambda \right)}{{}_{2}F_{1}\left({\tfrac {1}{2}},{\tfrac {1}{2}},1,\lambda \right)}}}
となる。
方法 2 : γ の 4次式を解く方法。
j
(
τ
)
=
27
(
1
+
8
γ
)
3
γ
(
1
−
γ
)
3
.
{\displaystyle j(\tau )={\frac {27(1+8\gamma )^{3}}{\gamma (1-\gamma )^{3}}}.}
任意の 4つの根 に対して、
τ
=
i
3
2
F
1
(
1
3
,
2
3
,
1
,
1
−
γ
)
2
F
1
(
1
3
,
2
3
,
1
,
γ
)
{\displaystyle \tau ={\frac {i}{\sqrt {3}}}{\frac {{}_{2}F_{1}\left({\tfrac {1}{3}},{\tfrac {2}{3}},1,1-\gamma \right)}{{}_{2}F_{1}\left({\tfrac {1}{3}},{\tfrac {2}{3}},1,\gamma \right)}}}
となる。
方法 3 : β の 3次式を解く方法。
j
(
τ
)
=
64
(
1
+
3
β
)
3
β
(
1
−
β
)
2
.
{\displaystyle j(\tau )={\frac {64(1+3\beta )^{3}}{\beta (1-\beta )^{2}}}.}
すると、任意の 3つの根に対し、
τ
=
i
2
2
F
1
(
1
4
,
3
4
,
1
,
1
−
β
)
2
F
1
(
1
4
,
3
4
,
1
,
β
)
{\displaystyle \tau ={\frac {i}{\sqrt {2}}}{\frac {{}_{2}F_{1}\left({\tfrac {1}{4}},{\tfrac {3}{4}},1,1-\beta \right)}{{}_{2}F_{1}\left({\tfrac {1}{4}},{\tfrac {3}{4}},1,\beta \right)}}}
となる。
方法 4 : α の 2次式を解く方法。
j
(
τ
)
=
1728
4
α
(
1
−
α
)
.
{\displaystyle j(\tau )={\frac {1728}{4\alpha (1-\alpha )}}.}
すると、
τ
=
i
2
F
1
(
1
6
,
5
6
,
1
,
1
−
α
)
2
F
1
(
1
6
,
5
6
,
1
,
α
)
{\displaystyle \tau =i\ {\frac {{}_{2}F_{1}\left({\tfrac {1}{6}},{\tfrac {5}{6}},1,1-\alpha \right)}{{}_{2}F_{1}\left({\tfrac {1}{6}},{\tfrac {5}{6}},1,\alpha \right)}}}
となる。
2つの根は τ と -1/τ であるが、j (τ) = j (-1/τ) であるために、どの α を選んでも差異はない。後半 3つの方法は、ラマヌジャン の交代基底についての楕円函数 論で発見された。
逆函数は、これらの根の比率が有界でないにもかかわらず、楕円函数の周期の高精度な計算を通して、うまく適用することが可能である。また、関連する帰結として、2 のべきの大きさをもつ虚数軸上の点で j の値が二次の根となることを通して(逆関数を)表すことができる(このようにして、定規とコンパスによる作図 が可能となる)。レベルが 2 のモジュラ函数 は 3次式であるので、この結果は自明ではない。
チュダノフスキー兄弟 (英語版 )
1
π
=
12
640320
3
/
2
∑
k
=
0
∞
(
6
k
)
!
(
163
⋅
3344418
k
+
13591409
)
(
3
k
)
!
(
k
!
)
3
(
−
640320
)
3
k
{\displaystyle {\frac {1}{\pi }}={\frac {12}{640320^{3/2}}}\sum _{k=0}^{\infty }{\frac {(6k)!(163\cdot 3344418k+13591409)}{(3k)!(k!)^{3}(-640320)^{3k}}}}
を発見し、
j
(
1
+
−
163
2
)
=
−
640320
3
{\displaystyle j{\big (}{\tfrac {1+{\sqrt {-163}}}{2}}{\big )}=-640320^{3}}
ラマヌジャン・佐藤級数 (英語版 )
次はリチャード・ボーチャーズ によって発見された[ 7]
j
(
τ
)
−
j
(
τ
′
)
=
1
q
∏
n
,
m
=
1
∞
(
1
−
q
n
q
′
m
)
c
n
m
{\displaystyle j(\tau )-j(\tau ')={1 \over q}\prod _{n,m=1}^{\infty }(1-q^{n}{q'}^{m})^{c_{nm}}}
である(ここでc_nはj関数のq展開におけるq^nの係数).
j-不変量は、基本領域 (英語版 )
1
2
(
1
+
i
3
)
{\displaystyle {\tfrac {1}{2}}\left(1+i{\sqrt {3}}\right)}
では 0 となる。
以下に、いくつかの特殊値を示す(J = j/1728 を使って表示している) [疑問点 – ノート 。
J
(
i
)
=
J
(
1
+
i
2
)
=
1
J
(
2
i
)
=
(
5
3
)
3
J
(
2
i
)
=
(
11
2
)
3
J
(
2
2
i
)
=
125
216
(
19
+
13
2
)
3
J
(
4
i
)
=
1
64
(
724
+
513
2
)
3
J
(
1
+
2
i
2
)
=
1
64
(
724
−
513
2
)
3
J
(
1
+
2
2
i
3
)
=
125
216
(
19
−
13
2
)
3
J
(
3
i
)
=
1
27
(
2
+
3
)
2
(
21
+
20
3
)
3
J
(
2
3
i
)
=
125
16
(
30
+
17
3
)
3
J
(
1
+
7
3
i
2
)
=
−
64000
7
(
651
+
142
21
)
3
J
(
1
+
3
11
i
10
)
=
64
27
(
23
−
4
33
)
2
(
−
77
+
15
33
)
3
J
(
21
i
)
=
1
128
(
3
+
7
)
5
(
17
+
7
3
+
59
7
+
35
21
)
3
J
(
30
i
1
)
=
1
4
(
7
+
5
2
+
3
5
+
2
10
)
4
(
55
+
30
2
+
12
5
+
10
10
)
3
J
(
30
i
2
)
=
1
4
(
7
+
5
2
−
3
5
−
2
10
)
4
(
55
+
30
2
−
12
5
−
10
10
)
3
J
(
30
i
5
)
=
1
4
(
7
−
5
2
+
3
5
−
2
10
)
4
(
55
−
30
2
+
12
5
−
10
10
)
3
J
(
30
i
10
)
=
1
4
(
7
−
5
2
−
3
5
+
2
10
)
4
(
55
−
30
2
−
12
5
+
10
10
)
3
J
(
1
+
31
i
2
)
=
(
1
−
(
1
+
19
2
(
13
−
93
13
+
93
⋅
31
+
27
31
−
27
3
+
13
+
93
13
−
93
⋅
31
−
27
31
+
27
3
)
)
2
)
3
J
(
5
i
)
=
(
1
+
9
4
5
(
13
+
5
5
)
2
)
3
J
(
5
i
+
1
2
)
=
(
1
−
9
4
5
(
13
−
5
5
)
2
)
3
J
(
6
i
)
=
1
216
(
2
+
3
)
10
(
231
+
380
3
+
(
204
+
158
3
)
12
4
)
3
J
(
70
i
)
=
(
1
+
9
4
(
303
+
220
2
+
139
5
+
96
10
)
2
)
3
J
(
94
i
)
=
(
1
+
9
8192
(
3
+
2
2
+
9
+
8
2
)
8
(
8
+
(
−
1
−
2
+
9
+
8
2
)
(
−
2
+
2
2
+
3
+
4
2
+
3
9
+
8
2
)
)
2
)
3
J
(
7
i
)
=
(
1
+
9
32
28
4
(
3
+
7
)
3
(
13
+
3
7
+
(
6
+
7
)
28
4
)
2
)
3
J
(
8
i
)
=
(
1
+
9
4
2
4
(
1
+
2
)
(
123
+
104
2
4
+
88
2
+
73
8
4
)
2
)
3
J
(
10
i
)
=
(
1
+
9
8
(
2402
+
1607
5
4
+
1074
25
4
+
719
125
4
)
2
)
3
J
(
5
i
2
)
=
(
1
+
9
8
(
2402
−
1607
5
4
+
1074
25
4
−
719
125
4
)
2
)
3
J
(
130
i
)
=
(
1
+
9
4
(
7392
+
3289
5
+
2040
13
+
917
65
)
2
)
3
J
(
190
i
)
=
(
1
+
18
(
31570
+
22323
2
+
14139
5
+
9998
10
)
2
)
3
J
(
2
58
i
)
=
(
1
+
9
256
(
1
+
2
)
5
(
5
+
29
)
5
(
793
+
907
2
+
237
29
+
103
58
)
2
)
3
J
(
1
+
1435
i
2
)
=
(
1
−
9
(
9892538
+
4424079
5
+
1544955
41
+
690925
205
)
2
)
3
J
(
1
+
1555
i
2
)
=
(
1
−
9
(
22297077
+
9971556
5
+
(
3571365
+
1597163
5
)
31
+
21
5
2
)
2
)
3
{\displaystyle {\begin{aligned}J(i)&=J\left({\tfrac {1+i}{2}}\right)=1\\J\left({\sqrt {2}}i\right)&={\big (}{\tfrac {5}{3}}{\big )}^{3}\\J(2i)&={\big (}{\tfrac {11}{2}}{\big )}^{3}\\J\left(2{\sqrt {2}}i\right)&={\tfrac {125}{216}}\left(19+13{\sqrt {2}}\right)^{3}\\J(4i)&={\tfrac {1}{64}}\left(724+513{\sqrt {2}}\right)^{3}\\J\left({\tfrac {1+2i}{2}}\right)&={\tfrac {1}{64}}\left(724-513{\sqrt {2}}\right)^{3}\\J\left({\tfrac {1+2{\sqrt {2}}i}{3}}\right)&={\tfrac {125}{216}}\left(19-13{\sqrt {2}}\right)^{3}\\J(3i)&={\tfrac {1}{27}}\left(2+{\sqrt {3}}\right)^{2}\left(21+20{\sqrt {3}}\right)^{3}\\J\left(2{\sqrt {3}}i\right)&={\tfrac {125}{16}}\left(30+17{\sqrt {3}}\right)^{3}\\J\left({\tfrac {1+7{\sqrt {3}}i}{2}}\right)&=-{\tfrac {64000}{7}}\left(651+142{\sqrt {21}}\right)^{3}\\J\left({\tfrac {1+3{\sqrt {11}}i}{10}}\right)&={\tfrac {64}{27}}\left(23-4{\sqrt {33}}\right)^{2}\left(-77+15{\sqrt {33}}\right)^{3}\\J\left({\sqrt {21}}i\right)&={\tfrac {1}{128}}\left(3+{\sqrt {7}}\right)^{5}\left(17+7{\sqrt {3}}+59{\sqrt {7}}+35{\sqrt {21}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{1}}\right)&={\tfrac {1}{4}}\left(7+5{\sqrt {2}}+3{\sqrt {5}}+2{\sqrt {10}}\right)^{4}\left(55+30{\sqrt {2}}+12{\sqrt {5}}+10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{2}}\right)&={\tfrac {1}{4}}\left(7+5{\sqrt {2}}-3{\sqrt {5}}-2{\sqrt {10}}\right)^{4}\left(55+30{\sqrt {2}}-12{\sqrt {5}}-10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{5}}\right)&={\tfrac {1}{4}}\left(7-5{\sqrt {2}}+3{\sqrt {5}}-2{\sqrt {10}}\right)^{4}\left(55-30{\sqrt {2}}+12{\sqrt {5}}-10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{10}}\right)&={\tfrac {1}{4}}\left(7-5{\sqrt {2}}-3{\sqrt {5}}+2{\sqrt {10}}\right)^{4}\left(55-30{\sqrt {2}}-12{\sqrt {5}}+10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {1+{\sqrt {31}}i}{2}}\right)&=\left(1-\left(1+{\frac {\sqrt {19}}{2}}\left({\sqrt {\tfrac {13-{\sqrt {93}}}{13+{\sqrt {93}}}}}\cdot {\sqrt[{3}]{\tfrac {{\sqrt {31}}+{\sqrt {27}}}{{\sqrt {31}}-{\sqrt {27}}}}}+{\sqrt {\tfrac {13+{\sqrt {93}}}{13-{\sqrt {93}}}}}\cdot {\sqrt[{3}]{\tfrac {{\sqrt {31}}-{\sqrt {27}}}{{\sqrt {31}}+{\sqrt {27}}}}}\right)\right)^{2}\right)^{3}\\J(5i)&=\left(1+{\tfrac {9}{4}}{\sqrt {5}}\left(13+5{\sqrt {5}}\right)^{2}\right)^{3}\\J\left({\tfrac {5i+1}{2}}\right)&=\left(1-{\tfrac {9}{4}}{\sqrt {5}}\left(13-5{\sqrt {5}}\right)^{2}\right)^{3}\\J(6i)&={\tfrac {1}{216}}\left(2+{\sqrt {3}}\right)^{10}\left(231+380{\sqrt {3}}+\left(204+158{\sqrt {3}}\right){\sqrt[{4}]{12}}\right)^{3}\\J({\sqrt {70}}i)&=\left(1+{\tfrac {9}{4}}\left(303+220{\sqrt {2}}+139{\sqrt {5}}+96{\sqrt {10}}\right)^{2}\right)^{3}\\J({\sqrt {94}}i)&=\left(1+{\tfrac {9}{8192}}\left(3+2{\sqrt {2}}+{\sqrt {9+8{\sqrt {2}}}}\right)^{8}\left(8+\left(-1-{\sqrt {2}}+{\sqrt {9+8{\sqrt {2}}}}\right)\left(-2+2{\sqrt {2}}+{\sqrt {3+4{\sqrt {2}}+3{\sqrt {9+8{\sqrt {2}}}}}}\right)\right)^{2}\right)^{3}\\J(7i)&=\left(1+{\tfrac {9}{32}}{\sqrt[{4}]{28}}\left(3+{\sqrt {7}}\right)^{3}\left(13+3{\sqrt {7}}+\left(6+{\sqrt {7}}\right){\sqrt[{4}]{28}}\right)^{2}\right)^{3}\\J(8i)&=\left(1+{\tfrac {9}{4}}{\sqrt[{4}]{2}}\left(1+{\sqrt {2}}\right)\left(123+104{\sqrt[{4}]{2}}+88{\sqrt {2}}+73{\sqrt[{4}]{8}}\right)^{2}\right)^{3}\\J(10i)&=\left(1+{\tfrac {9}{8}}\left(2402+1607{\sqrt[{4}]{5}}+1074{\sqrt[{4}]{25}}+719{\sqrt[{4}]{125}}\right)^{2}\right)^{3}\\J\left({\tfrac {5i}{2}}\right)&=\left(1+{\tfrac {9}{8}}\left(2402-1607{\sqrt[{4}]{5}}+1074{\sqrt[{4}]{25}}-719{\sqrt[{4}]{125}}\right)^{2}\right)^{3}\\J({\sqrt {130}}i)&=\left(1+{\tfrac {9}{4}}\left(7392+3289{\sqrt {5}}+2040{\sqrt {13}}+917{\sqrt {65}}\right)^{2}\right)^{3}\\J({\sqrt {190}}i)&=\left(1+18\left(31570+22323{\sqrt {2}}+14139{\sqrt {5}}+9998{\sqrt {10}}\right)^{2}\right)^{3}\\J(2{\sqrt {58}}i)&=\left(1+{\tfrac {9}{256}}\left(1+{\sqrt {2}}\right)^{5}\left(5+{\sqrt {29}}\right)^{5}\left(793+907{\sqrt {2}}+237{\sqrt {29}}+103{\sqrt {58}}\right)^{2}\right)^{3}\\J\left({\tfrac {1+{\sqrt {1435}}i}{2}}\right)&=\left(1-9\left(9892538+4424079{\sqrt {5}}+1544955{\sqrt {41}}+690925{\sqrt {205}}\right)^{2}\right)^{3}\\J\left({\tfrac {1+{\sqrt {1555}}i}{2}}\right)&=\left(1-9\left(22297077+9971556{\sqrt {5}}+\left(3571365+1597163{\sqrt {5}}\right){\sqrt {\tfrac {31+21{\sqrt {5}}}{2}}}\right)^{2}\right)^{3}\\\end{aligned}}}
2014年にはいくつかの特殊値が計算された[ 8]
J
(
5
i
+
2
4
)
=
(
1
−
9
(
1
+
5
)
38
2
41
2
(
7485
−
762
2
+
1479
5
−
3072
10
−
5
4
(
178
−
2221
2
+
3148
5
−
1289
10
)
)
2
)
3
J
(
10
i
+
1
2
)
=
(
1
−
9
(
1
+
5
)
38
2
41
2
(
7485
−
762
2
+
1479
5
−
3072
10
+
5
4
(
178
−
2221
2
+
3148
5
−
1289
10
)
)
2
)
3
J
(
5
i
4
)
=
(
1
+
9
(
1
+
5
)
38
2
41
2
(
7485
+
762
2
+
1479
5
+
3072
10
−
5
4
(
178
+
2221
2
+
3148
5
+
1289
10
)
)
2
)
3
J
(
20
i
)
=
(
1
+
9
(
1
+
5
)
38
2
41
2
(
7485
+
762
2
+
1479
5
+
3072
10
+
5
4
(
178
+
2221
2
+
3148
5
+
1289
10
)
)
2
)
3
{\displaystyle {\begin{aligned}J\left({\tfrac {5i+2}{4}}\right)&=\left(1-{\tfrac {9\left(1+{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485-762{\sqrt {2}}+1479{\sqrt {5}}-3072{\sqrt {10}}-{\sqrt[{4}]{5}}\left(178-2221{\sqrt {2}}+3148{\sqrt {5}}-1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\\J\left({\tfrac {10i+1}{2}}\right)&=\left(1-{\tfrac {9\left(1+{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485-762{\sqrt {2}}+1479{\sqrt {5}}-3072{\sqrt {10}}+{\sqrt[{4}]{5}}\left(178-2221{\sqrt {2}}+3148{\sqrt {5}}-1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\\J\left({\tfrac {5i}{4}}\right)&=\left(1+{\tfrac {9\left(1+{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485+762{\sqrt {2}}+1479{\sqrt {5}}+3072{\sqrt {10}}-{\sqrt[{4}]{5}}\left(178+2221{\sqrt {2}}+3148{\sqrt {5}}+1289{\sqrt {10}}\right){\Big )}^{2}\right)^{3}\\J(20i)&=\left(1+{\tfrac {9\left(1+{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485+762{\sqrt {2}}+1479{\sqrt {5}}+3072{\sqrt {10}}+{\sqrt[{4}]{5}}\left(178+2221{\sqrt {2}}+3148{\sqrt {5}}+1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\end{aligned}}}
これ以前に示したすべての値は実数である。複素共役のペアは、
J
(
10
i
)
{\displaystyle J(10i)}
J
(
5
i
/
2
)
{\displaystyle J(5i/2)}
J
(
5
i
±
1
4
)
=
(
1
−
9
8
(
(
2402
−
1074
5
)
i
±
(
1607
−
719
5
)
5
4
)
2
)
3
{\displaystyle {\begin{aligned}J\left({\tfrac {5i\pm 1}{4}}\right)&=\left(1-{\tfrac {9}{8}}\left((2402-1074{\sqrt {5}})i\pm (1607-719{\sqrt {5}}){\sqrt[{4}]{5}}\right)^{2}\right)^{3}\end{aligned}}}
4つの特殊値は、2つの複素共役のペアにより与えられる[ 9]
J
(
4
(
5
i
±
1
)
13
)
=
(
1
−
9
(
1
−
5
)
38
2
41
2
(
7485
−
762
2
−
1479
5
+
3072
10
±
i
5
4
(
178
−
2221
2
−
3148
5
+
1289
10
)
)
2
)
3
J
(
5
(
4
i
±
1
)
17
)
=
(
1
+
9
(
1
−
5
)
38
2
41
2
(
7485
+
762
2
−
1479
5
−
3072
10
±
i
5
4
(
178
+
2221
2
−
3148
5
−
1289
10
)
)
2
)
3
{\displaystyle {\begin{aligned}J\left({\tfrac {4\left(5i\pm 1\right)}{13}}\right)=\left(1-{\tfrac {9\left(1-{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485-762{\sqrt {2}}-1479{\sqrt {5}}+3072{\sqrt {10}}\pm i{\sqrt[{4}]{5}}\left(178-2221{\sqrt {2}}-3148{\sqrt {5}}+1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\\J\left({\tfrac {5\left(4i\pm 1\right)}{17}}\right)=\left(1+{\tfrac {9\left(1-{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485+762{\sqrt {2}}-1479{\sqrt {5}}-3072{\sqrt {10}}\pm i{\sqrt[{4}]{5}}\left(178+2221{\sqrt {2}}-3148{\sqrt {5}}-1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\end{aligned}}}
^ Silverman, Joseph H. (1986). The Arithmetic of Elliptic Curves . Graduate Texts in Mathematics . 106 . Springer-Verlag . p. 339. ISBN 0-387-96203-4 . Zbl 0585.14026 ^ Petersson, Hans (1932). Über die Entwicklungskoeffizienten der automorphen Formen . 58 . 169–215. doi :10.1007/BF02547776 . MR 1555346 ^ Rademacher, Hans (1938). The Fourier coefficients of the modular invariant j(τ) . 60 . The Johns Hopkins University Press. 501–512. doi :10.2307/2371313 . JSTOR 2371313 . MR 1507331 ^ Chandrasekharan (1985) p.108
^ Chandrasekharan, K. (1985), Elliptic Functions , Grundlehren der mathematischen Wissenschaften, 281 , Springer-Verlag , p. 110, ISBN 3-540-15295-4 , Zbl 0575.33001 ^ Girondo, Ernesto; González-Diez, Gabino (2012), Introduction to compact Riemann surfaces and dessins d'enfants , London Mathematical Society Student Texts, 79 , Cambridge: Cambridge University Press , p. 267, ISBN 978-0-521-74022-7 , Zbl 1253.30001 ^ Borcherds, R.E. (1992). Monstrous moonshine and monstrous Lie superalgebras . 60 . 405–
444. ^ Adlaj, Semjon. “Multiplication and division on elliptic curves, torsion points and roots of modular equations ”. 17 October 2014 閲覧。 ^ Adlaj, Semjon (2014年). “Torsion points on elliptic curves and modular polynomial symmetries ”. 2014年10月15日 閲覧。
Apostol, Tom M. (1976), Modular functions and Dirichlet Series in Number Theory , Graduate Texts in Mathematics, 41 , New York: Springer-Verlag, MR 0422157 Berndt, Bruce C. ; Chan, Heng Huat (1999), “Ramanujan and the modular j-invariant” , Canadian Mathematical Bulletin 42 (4): 427–440, doi :10.4153/CMB-1999-050-1 , MR 1727340 , http://www.journals.cms.math.ca/cgi-bin/vault/public/view/berndt7376/body/PDF/berndt7376.pdf Cox, David A. (1989), Primes of the Form x^2 + ny^2: Fermat, Class Field Theory, and Complex Multiplication , New York: Wiley-Interscience Publication, John Wiley & Sons Inc., MR 1028322 Conway, John Horton ; Norton, Simon (1979), “Monstrous moonshine”, Bulletin of the London Mathematical Society 11 (3): 308–339, doi :10.1112/blms/11.3.308 , MR 0554399 Rankin, Robert A. (1977), Modular forms and functions , Cambridge: Cambridge University Press, ISBN 0-521-21212-X , MR 0498390 Schneider, Theodor (1937), “Arithmetische Untersuchungen elliptischer Integrale”, Math. Annalen 113 : 1–13, doi :10.1007/BF01571618 , MR 1513075 
















































![{\displaystyle {\begin{aligned}J(i)&=J\left({\tfrac {1+i}{2}}\right)=1\\J\left({\sqrt {2}}i\right)&={\big (}{\tfrac {5}{3}}{\big )}^{3}\\J(2i)&={\big (}{\tfrac {11}{2}}{\big )}^{3}\\J\left(2{\sqrt {2}}i\right)&={\tfrac {125}{216}}\left(19+13{\sqrt {2}}\right)^{3}\\J(4i)&={\tfrac {1}{64}}\left(724+513{\sqrt {2}}\right)^{3}\\J\left({\tfrac {1+2i}{2}}\right)&={\tfrac {1}{64}}\left(724-513{\sqrt {2}}\right)^{3}\\J\left({\tfrac {1+2{\sqrt {2}}i}{3}}\right)&={\tfrac {125}{216}}\left(19-13{\sqrt {2}}\right)^{3}\\J(3i)&={\tfrac {1}{27}}\left(2+{\sqrt {3}}\right)^{2}\left(21+20{\sqrt {3}}\right)^{3}\\J\left(2{\sqrt {3}}i\right)&={\tfrac {125}{16}}\left(30+17{\sqrt {3}}\right)^{3}\\J\left({\tfrac {1+7{\sqrt {3}}i}{2}}\right)&=-{\tfrac {64000}{7}}\left(651+142{\sqrt {21}}\right)^{3}\\J\left({\tfrac {1+3{\sqrt {11}}i}{10}}\right)&={\tfrac {64}{27}}\left(23-4{\sqrt {33}}\right)^{2}\left(-77+15{\sqrt {33}}\right)^{3}\\J\left({\sqrt {21}}i\right)&={\tfrac {1}{128}}\left(3+{\sqrt {7}}\right)^{5}\left(17+7{\sqrt {3}}+59{\sqrt {7}}+35{\sqrt {21}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{1}}\right)&={\tfrac {1}{4}}\left(7+5{\sqrt {2}}+3{\sqrt {5}}+2{\sqrt {10}}\right)^{4}\left(55+30{\sqrt {2}}+12{\sqrt {5}}+10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{2}}\right)&={\tfrac {1}{4}}\left(7+5{\sqrt {2}}-3{\sqrt {5}}-2{\sqrt {10}}\right)^{4}\left(55+30{\sqrt {2}}-12{\sqrt {5}}-10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{5}}\right)&={\tfrac {1}{4}}\left(7-5{\sqrt {2}}+3{\sqrt {5}}-2{\sqrt {10}}\right)^{4}\left(55-30{\sqrt {2}}+12{\sqrt {5}}-10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{10}}\right)&={\tfrac {1}{4}}\left(7-5{\sqrt {2}}-3{\sqrt {5}}+2{\sqrt {10}}\right)^{4}\left(55-30{\sqrt {2}}-12{\sqrt {5}}+10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {1+{\sqrt {31}}i}{2}}\right)&=\left(1-\left(1+{\frac {\sqrt {19}}{2}}\left({\sqrt {\tfrac {13-{\sqrt {93}}}{13+{\sqrt {93}}}}}\cdot {\sqrt[{3}]{\tfrac {{\sqrt {31}}+{\sqrt {27}}}{{\sqrt {31}}-{\sqrt {27}}}}}+{\sqrt {\tfrac {13+{\sqrt {93}}}{13-{\sqrt {93}}}}}\cdot {\sqrt[{3}]{\tfrac {{\sqrt {31}}-{\sqrt {27}}}{{\sqrt {31}}+{\sqrt {27}}}}}\right)\right)^{2}\right)^{3}\\J(5i)&=\left(1+{\tfrac {9}{4}}{\sqrt {5}}\left(13+5{\sqrt {5}}\right)^{2}\right)^{3}\\J\left({\tfrac {5i+1}{2}}\right)&=\left(1-{\tfrac {9}{4}}{\sqrt {5}}\left(13-5{\sqrt {5}}\right)^{2}\right)^{3}\\J(6i)&={\tfrac {1}{216}}\left(2+{\sqrt {3}}\right)^{10}\left(231+380{\sqrt {3}}+\left(204+158{\sqrt {3}}\right){\sqrt[{4}]{12}}\right)^{3}\\J({\sqrt {70}}i)&=\left(1+{\tfrac {9}{4}}\left(303+220{\sqrt {2}}+139{\sqrt {5}}+96{\sqrt {10}}\right)^{2}\right)^{3}\\J({\sqrt {94}}i)&=\left(1+{\tfrac {9}{8192}}\left(3+2{\sqrt {2}}+{\sqrt {9+8{\sqrt {2}}}}\right)^{8}\left(8+\left(-1-{\sqrt {2}}+{\sqrt {9+8{\sqrt {2}}}}\right)\left(-2+2{\sqrt {2}}+{\sqrt {3+4{\sqrt {2}}+3{\sqrt {9+8{\sqrt {2}}}}}}\right)\right)^{2}\right)^{3}\\J(7i)&=\left(1+{\tfrac {9}{32}}{\sqrt[{4}]{28}}\left(3+{\sqrt {7}}\right)^{3}\left(13+3{\sqrt {7}}+\left(6+{\sqrt {7}}\right){\sqrt[{4}]{28}}\right)^{2}\right)^{3}\\J(8i)&=\left(1+{\tfrac {9}{4}}{\sqrt[{4}]{2}}\left(1+{\sqrt {2}}\right)\left(123+104{\sqrt[{4}]{2}}+88{\sqrt {2}}+73{\sqrt[{4}]{8}}\right)^{2}\right)^{3}\\J(10i)&=\left(1+{\tfrac {9}{8}}\left(2402+1607{\sqrt[{4}]{5}}+1074{\sqrt[{4}]{25}}+719{\sqrt[{4}]{125}}\right)^{2}\right)^{3}\\J\left({\tfrac {5i}{2}}\right)&=\left(1+{\tfrac {9}{8}}\left(2402-1607{\sqrt[{4}]{5}}+1074{\sqrt[{4}]{25}}-719{\sqrt[{4}]{125}}\right)^{2}\right)^{3}\\J({\sqrt {130}}i)&=\left(1+{\tfrac {9}{4}}\left(7392+3289{\sqrt {5}}+2040{\sqrt {13}}+917{\sqrt {65}}\right)^{2}\right)^{3}\\J({\sqrt {190}}i)&=\left(1+18\left(31570+22323{\sqrt {2}}+14139{\sqrt {5}}+9998{\sqrt {10}}\right)^{2}\right)^{3}\\J(2{\sqrt {58}}i)&=\left(1+{\tfrac {9}{256}}\left(1+{\sqrt {2}}\right)^{5}\left(5+{\sqrt {29}}\right)^{5}\left(793+907{\sqrt {2}}+237{\sqrt {29}}+103{\sqrt {58}}\right)^{2}\right)^{3}\\J\left({\tfrac {1+{\sqrt {1435}}i}{2}}\right)&=\left(1-9\left(9892538+4424079{\sqrt {5}}+1544955{\sqrt {41}}+690925{\sqrt {205}}\right)^{2}\right)^{3}\\J\left({\tfrac {1+{\sqrt {1555}}i}{2}}\right)&=\left(1-9\left(22297077+9971556{\sqrt {5}}+\left(3571365+1597163{\sqrt {5}}\right){\sqrt {\tfrac {31+21{\sqrt {5}}}{2}}}\right)^{2}\right)^{3}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/969a1013599eecc294a857391fee5d3eba91ed6f)
![{\displaystyle {\begin{aligned}J\left({\tfrac {5i+2}{4}}\right)&=\left(1-{\tfrac {9\left(1+{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485-762{\sqrt {2}}+1479{\sqrt {5}}-3072{\sqrt {10}}-{\sqrt[{4}]{5}}\left(178-2221{\sqrt {2}}+3148{\sqrt {5}}-1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\\J\left({\tfrac {10i+1}{2}}\right)&=\left(1-{\tfrac {9\left(1+{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485-762{\sqrt {2}}+1479{\sqrt {5}}-3072{\sqrt {10}}+{\sqrt[{4}]{5}}\left(178-2221{\sqrt {2}}+3148{\sqrt {5}}-1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\\J\left({\tfrac {5i}{4}}\right)&=\left(1+{\tfrac {9\left(1+{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485+762{\sqrt {2}}+1479{\sqrt {5}}+3072{\sqrt {10}}-{\sqrt[{4}]{5}}\left(178+2221{\sqrt {2}}+3148{\sqrt {5}}+1289{\sqrt {10}}\right){\Big )}^{2}\right)^{3}\\J(20i)&=\left(1+{\tfrac {9\left(1+{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485+762{\sqrt {2}}+1479{\sqrt {5}}+3072{\sqrt {10}}+{\sqrt[{4}]{5}}\left(178+2221{\sqrt {2}}+3148{\sqrt {5}}+1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bba1c724ceb674a5a3f4a7c5831fea7b9734e6d)


![{\displaystyle {\begin{aligned}J\left({\tfrac {5i\pm 1}{4}}\right)&=\left(1-{\tfrac {9}{8}}\left((2402-1074{\sqrt {5}})i\pm (1607-719{\sqrt {5}}){\sqrt[{4}]{5}}\right)^{2}\right)^{3}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5566614a3b8aca7521b71e8d9068b85a85f1a52b)
![{\displaystyle {\begin{aligned}J\left({\tfrac {4\left(5i\pm 1\right)}{13}}\right)=\left(1-{\tfrac {9\left(1-{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485-762{\sqrt {2}}-1479{\sqrt {5}}+3072{\sqrt {10}}\pm i{\sqrt[{4}]{5}}\left(178-2221{\sqrt {2}}-3148{\sqrt {5}}+1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\\J\left({\tfrac {5\left(4i\pm 1\right)}{17}}\right)=\left(1+{\tfrac {9\left(1-{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485+762{\sqrt {2}}-1479{\sqrt {5}}-3072{\sqrt {10}}\pm i{\sqrt[{4}]{5}}\left(178+2221{\sqrt {2}}-3148{\sqrt {5}}-1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fb9310e34bda283dfbb8bbaf8c4e252ed771a0f)