射影極限
数学における逆極限(ぎゃくきょくげん、英: inverse limit)あるいは射影極限(しゃえいきょくげん、英: projective limit)は、正確な言い方ではないが、いくつかの関連する対象を「貼合せる」ような構成法であり、貼合せの具体的な方法は対象の間の射によって決められている。逆極限は任意の圏において考えることができる。
厳密な定義[編集]
代数系の射影極限[編集]
まず群と準同型からなる逆系 (inverse system) あるいは射影系 (projective system) と呼ばれるものの定義から始める。(I, ≤) を有向半順序集合とする(I が有向集合であることを課さない文献もある)。群の族 (Ai)i∈I と準同型の族 fij: Aj → Ai (i ≤ j) で以下の性質、
- fii は Ai における恒等写像、
- fik = fij ∘ fjk (i ≤ j ≤ k)
を満たすものが与えられたとき、対 ((Ai)i∈I, (fij)i≤ j∈I) を群と準同型の成す I 上の逆系と呼び、各射 fij はこの系の遷移射 (transition morphisms) と呼ぶ。
逆系 ((Ai)i∈I, (fij)i≤ j∈I) の逆極限(射影極限)は Ai たちの直積の特定の部分群
として定義される。この射影極限 A は(I の各 i に対して直積の i-成分を取り出すという)自然な射影 πi: A → Ai を備えている。射影極限と自然な射影は、次節に述べる普遍性を満足する。
これと同じ構成法は、Ai たちが集合や環あるいは(適当に固定した環上の)加群、多元環などの場合にも、それぞれの意味での準同型を射として行うことができて、得られる逆極限はそれぞれの圏に属する対象となる。
一般の定義[編集]
逆極限は、任意の圏において普遍性を用いて抽象的に定義することができる。 (Xi, fij) を圏 C の対象と射からなる逆系(逆系の意味は前節と同じ)とすると、この逆系の逆極限(射影極限)とは、C の適当な対象 X と射影と総称される射の族 πi: X → Xi で πi = fij ∘ πj を任意の i ≤ j に対して満たすものとの対 (X, πi) であって、次のような意味で普遍性を満足するものをいう。すなわち、同様の対 (Y, ψi) があれば、射 u: Y → X が一意的に存在して図式
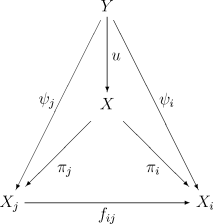
は全ての i ≤ j に対して可換になる。逆系 (Xi, fij) が既知であるとき、その逆極限 X をしばしば
で表す。
前節の場合と異なり、任意の圏においては逆極限が存在しないことが起こりうるが、しかし存在する場合は強い意味で一意である。すなわち、逆極限 X とは別の逆極限 X′ が任意に与えられたとき、全ての射影に対して可換となる射 X′ → X が一意的に存在する。
圏 C における逆系は、函手の言葉で記述することもできる。任意の半順序集合 I は「i → j ⇔ i ≤ j」によって射の集合を定めた小さい圏と見なすことができるから、逆系とは反変函手 I → C に他ならない。そして、逆極限函手
は共変函手となる。
例[編集]
- Ai を長さiの有限数列全体からなる集合、fij (i≤j) を数列をi項に切り詰める写像とすると、その射影極限は、数列全体の集合となる。
- p-進整数全体の成す環 Zp は、自然数全体に通常の順序を入れたものを添字集合とする整数環の剰余類環の族 Z/pnZ でそれらの間の射として、「剰余の取替え」で得られる準同型をとったものの成す射影系から射影極限として得られる。p-進整数環における自然な位相は、射影極限としての位相に一致する。
- 可換環 R 上の形式冪級数環 R[[t]] は、自然数の全体に通常の順序を入れたもので添字付けられる、環の族 R[t]/tnR[t] が自然な射影 を射として成す射影系の射影極限と見なすことができる。
- 副有限群は(離散)有限群の射影極限として定義される。
- 逆系 (Xi, fij) の添字集合 I が最大元 m を持つならば、射影極限 X からの自然な射影 πm: X → Xm は同型である。
- 位相空間の圏における逆極限は、逆系の各台集合に対して単に集合としての逆極限をとったものを台集合とし、それに始位相を入れて得られる位相空間である。これは極限位相としても知られる。
- 添字集合が自明な順序を持つ(つまり有向でない集合)とすると、そのような任意の逆系に対応する逆極限は単なる直積である。
- 三つの元からなる添字集合 I = {i, j, k} で i ≤ j かつ i ≤ k とする(これも有向集合ではない)と、そのような任意の逆系の逆極限は引戻しである。
射影極限の導来函手[編集]
アーベル圏 C に対して、逆極限函手
は左完全である。I が可算順序集合(単に半順序が入っているというのではない)で、C がアーベル群の圏 Ab のとき、ミッタークレフラー条件とは の完全性を保証するような遷移射 fij に関する条件である。
以下具体的に述べる。アイレンベルグは函手
で、三つのアーベル群の逆系(Ai, fij), (Bi, gij), (Ci, hij) が短完全列
を成すならば、
が Ab における完全列となるというものを構成した。
- ミッターク=レフラー条件
- アーベル群の逆系 (Ai, fij) の射の値域が安定(すなわち、各 k に対して、適当な j ≥ k が存在して「i ≥ j なる全ての i について が成り立つ」)ならば、この逆系はミッターク=レフラー条件を満足するという。この条件は なることを含意する。
次のような状況は、ミッターク=レフラー条件を満たす例となっている。
- 全ての射 fij が全射であるような逆系
- 有限次元ベクトル空間の成す逆系
また、lim1 が 0 とならない(したがってミッターク=レフラー条件を満足しない)例として、I は非負整数の全体、Ai = piZ, Bi = Z, Ci = Bi/Ai = Z/piZ とすれば、
が得られる。ここで Zp は p-進整数環を表す。
更なる結果[編集]
もっと一般に、C が十分多くの入射対象を持つアーベル圏ならば、CI もそうで、従って射影極限函手の右導来函手が定まる。 n-次の右導来函手を
で表す。C がグロタンディークの公理 (AB4*) を満足する場合には、ジャン=エリック・ルースが AbI 上の函手 lim1を
なる函手の系列 limn へ一般化した。ルースは凡そ40年を掛け、Roos (1961)「lim の導来函手における応用」において、I が非負整数で遷移射が全射となるような逆系(ミッターク=レフラー列) (Ai, fij) に対して、lim1 Ai = 0 となることを示した。しかし、2002年にアムノン・ニーマンとピエール・ドリーニュは (AB4*) に加えて (AB4) を満足する圏における同様の逆系でlim1 Ai ≠ 0 なる例を構成する。その後ルースは、Roos (2006)「逆極限の導来函手再考」において、彼の結果は((AB3) と (AB4*) に加えて)C が生成系を持つならば正しくなるということを示した。
バリー・ミッチェルは、"The cohomological dimension of a directed set"(「有向集合のコホモロジー次元」)において、I が 濃度 ℵd(d 番目のアレフ数)を持つならば、Rnlim は n ≥ d + 2 なる全ての n について 0 になることを示した。これは可換環 R 上の R-加群の圏 R-Mod において I で添字付けられた図式に適用することができる。ここで R-加群の圏でなく任意のアーベル圏とすると必ずしも成立しない(可算集合で添字付けられる図式上で limn が 0 とならないようなアーベル圏の例については (Roos 2006) を参照)。
関連概念と一般化[編集]
射影極限(逆極限)の圏論的双対は帰納極限(順極限、直極限)であり、圏論においてはより一般の極限と余極限として捉えることができる。用語法が少し紛らわしいが、逆極限は(圏論的)極限であって、余極限ではないことに注意。
参考文献[編集]
- Bourbaki, Nicolas (1989), Algebra I, Springer, ISBN 978-3540642435, OCLC 40551484
- Bourbaki, Nicolas (1989), General topology: Chapters 1-4, Springer, ISBN 978-3540642411, OCLC 40551485
- Mac Lane, Saunders (September 1998), Categories for the Working Mathematician (2nd ed.), Springer, ISBN 0-387-98403-8, 日本語訳: 三好博之・高木理 訳『圏論の基礎』シュプリンガーフェアラーク東京、2005年。
- Mitchell, Barry (1972), “Rings with several objects”, Advances in Mathematics 8: 1–161, doi:10.1016/0001-8708(72)90002-3, MR0294454
- Neeman, Amnon (2002), “A counterexample to a 1962 "theorem" in homological algebra (with appendix by Pierre Deligne)”, Inventiones Mathematicae 148 (2): 397–420, doi:10.1007/s002220100197, MR1906154
- Roos, Jan-Erik (1961), “Sur les foncteurs dérivés de lim. Applications”, C. R. Acad. Sci. Paris 252: 3702–3704, MR0132091
- Roos, Jan-Erik (2006), “Derived functors of inverse limits revisited”, J. London Math. Soc. (2) 73 (1): 65–83, doi:10.1112/S0024610705022416, MR2197371
- Section 3.5 of Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, 38, Cambridge University Press, ISBN 978-0-521-55987-4, OCLC 36131259, MR1269324




![{\displaystyle R[t]/t^{n+j}R[t]\to R[t]/t^{n}R[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d38ca7b8cab6419250ecf7139540414bb3691290)









