回転 (ベクトル解析)
ベクトル解析における回転(かいてん、英: rotation, curl)rot(または curl)は、三次元ベクトル場の無限小回転を記述するベクトル演算子である。
ベクトル場の各点において、ベクトル場の回転はベクトルとして表され、このベクトルの寄与(大きさと向き)によってその点での回転が特徴付けられる。
概要[編集]
回転ベクトルの向きは回転軸に沿って右手系となる方にとり、回転ベクトルの大きさは回転の大きさとなる。例えば、与えられたベクトル場が、動いている流体の流速を表すものであるとき、その回転とはその流体の循環密度のことになる。回転場が 0 となるベクトル場は無回転であると言う。
場の回転はベクトル場に対する導函数に相当し、これに対応して微分積分学の基本定理に相当するのは、ベクトル場の回転場の面積分をそのベクトル場の境界曲線上での線積分と関係づけるストークスの定理(ストークス=ケルビンの定理)であると考えられる。
回転演算に相当する用語は curl, rotation の他に rotor や rotational などがあり、記法 curl F に相当する記法は rot F や ∇ × F などがある。前者の rot 系の用語・記法を用いる流儀はヨーロッパ諸国の系統に多く、ナブラや交叉積を用いる記法はそれ以外の系統で使われる傾向にある。
勾配や発散とは異なり、回転の概念を単純に高次元化することはできない。ただし、三次元に限らないある種の一般化は可能で、それはベクトル場の回転がまたベクトル場となるように幾何学的に定義される。これは三次元交叉積がそうであるのと同様の現象であり、このことは回転を “∇×” で表す記法にも表れている。
回転 “curl” の名を最初に提示したものはジェームズ・クラーク・マクスウェルで1871年のことである[1]。
定義[編集]
ベクトル場 F の回転は、curl F または ∇ × F と書かれ、各点での値はその点を通る無数の直線の上への射影によって定義される。その点を始点とする任意の単位ベクトル n̂ に対し、F の回転の n̂ の上への射影は n̂ に直交する平面内の閉路上の積分を積分路が囲む面積で割った値の、積分路をその点へ無限に近づけるときの極限値として定義される。こうして定義される回転作用素 curl はC1-級写像 R3 → R3 を C0-級写像 R3 → R3 へ写す。

同じことだが式で書けば、
によって curl は陰に定義されるのである[2][3]。ここで右辺の は、問題の領域の境界に沿った線積分であり、|A| はその領域の面積の大きさである。ν̂ が領域の外側を向いた平面内の法線のとき、n̂ がこの平面に直交する単位ベクトルである限りにおいて、積分路 C の向きは、C の接ベクトル ω̂ が正の向きであることを、三つ組 (n̂, ν̂, ω̂) が R3 の正に向き付けられた基底(右手系)を成すことを以って定める。
上記の公式は、ベクトル場の回転というものが、その場の「循環」の無限小面積密度として定義されることを意味するものである。この定義は自然に、
- 対応する大域公式としてのケルビン・ストークスの定理、
- 以下に挙げる曲線直交座標系における「覚えやすい」定義
とも適合する。後者の座標系の話は、例えばデカルト座標系、球面座標系、円筒座標系、あるいは楕円座標系や抛物座標系の場合にも
が成り立つ。ここで、(x1, x2, x3) がデカルト座標系で (u1, u2, u3) が直交座標系ならば、
は ui に対応する座標ベクトルの長さである。他の成分に関しても、添字の輪環の順で 3,1,2 → 1,2,3 → 2,3,1 と置き換えれば同様である。
直観的解釈[編集]
ベクトル場が(液体や気体の巨大タンクのような)流量の速度場を記述するもので、その流体の中に(中心が特定の点に固定された)小さなボールが浮かんでいると仮定する。ボールの表面がデコボコならば、そこを通過する流体によってボールは回転するはずである。その回転軸は(向きは右手系に従うものとして)ボールの中心から場の回転ベクトルの方向を指し、回転の角速度はその点における回転ベクトルの大きさの半分に等しい[4]。
用語法について[編集]
実用に際しては、ほぼ全ての場合において適当な曲線座標系の下で回転作用素を適用することになり、その場合はより平易な表現を導出することができるので、上記の定義をそのまま適用する場面と言うのは希である。
記法 ∇ × F は三次元交叉積との類推が元になっており、∇ をベクトル微分作用素のナブラと考えれば直交座標系における回転作用素の表示に対する記憶術として有効なものである。作用素に対する演算を施すような記法は物理学や代数学では広く用いられる。しかし、ある種の複雑な座標系、例えば(プラズマ物理学で一般的な)極トロイド座標系 (polar-toroidal coordinates) などを考えているときには、記法 ∇ × F を斯くの如き作用素同士の演算と解釈したのでは誤った結果を導くことになる。
直交座標系に関して ∇ × F を展開すれば、ベクトル場 F = (Fx, Fy, Fz) に対して、
と書くことができる。ただし、i, j, k はそれぞれ x-軸、y-軸、z-軸方向の単位ベクトルである。
これは
と書くことと同じである[5]。これは座標を用いた表示だけれども、この式が座標軸に関する真の回転に対しては不変であり、座標軸に関する鏡映では符号が反転することが確認できる。
一般の座標系における回転は
で与えられる[6]。ここで、ε はエディントンのイプシロンであり、この計量テンソルは F の下付き添字に対するものとして用いられる。またアインシュタインの和の規約に従って和の記号は省略した。
この式はつまり、各座標ベクトル場を ek とすれば
であることを言っているのである。
これはまた、外微分を用いて
と書くこともできる。ここで、 と は添字の上げ下げ同型であり、 はホッジ・スターとする。
この公式を見れば一般座標系で F の回転をどのように計算すべきかがわかり、回転作用素を任意の向きを持つ三次元リーマン多様体に対して一般化することができる。これは向きに依存するから、回転は掌性演算、即ち向きを逆にすれば回転の向きも同じく逆になる。
例[編集]
単純なベクトル場[編集]
x と y に線型に依存するベクトル場
をとれば、これは

のような様子で、見た目通りこの場が「回転」していることがわかる。この場に、どこでもよいから外輪 (paddle wheel) を置けば、外輪が時計回りに回転することはすぐに分かる。右手系に従うならば、この「回転」は、画面に向かって垂直に入る向きであることが期待される。右手系に座標系を取るのであれば、画面へ垂直に向かっていく方向は負の z-方向である。ここに x, y が出てこない(xy-平面に直交する)ことは交叉積と同様である。
さて、この場の回転を計算すれば、
となり、これは期待した通り、実際に負の z 方向を指す。上記の回転量はどの点 (x, y) でも同じであり、F の回転を図にしたものは非常につまらないものになる:

少し複雑な例[編集]
少し状況を複雑にして、ベクトル場
を考える。これは以下の図

のような場である。これは一見して回転を見つけることができないかもしれないが、例えば右側をよく見ると、この場は x = 3における値よりも x = 4 における値の方が大きい。直観的にはこの部分に小さな外輪を置けば、右側の流量が大きいので時計回りに回転し始めることがわかる。これは回転ベクトルが z が負の向きを持つことを意味する。対照的に左の方を見れば、ここに外輪を置いたとき左側の流量が多いので、外輪は反時計回りに回転し、回転ベクトルは z が正の向きを持つ。これらの直観を裏打ちするように、
が成り立ち、期待した通り実際にこの回転場は負の x に対して z の正方向を持ち、正の x に対して z の負方向を持つ。この回転はどこでも同じではないから、少しは意味のある形になる:
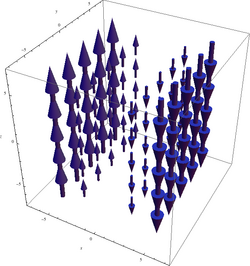
この回転場の図が当然の如く y にも z にも依存しないものになっていること、および正の x に対して負の z-方向、負の x に対して正の z-方向を向いていることに注意。
主な恒等式[編集]
例えば ∇ ×(v × F) を考える。デカルト座標系に従えば、これは
となることが示される。この場合はベクトル場 v と ∇ とを入れ替えて
とすることができる。ここで、ファインマンの下付き添字記法 ∇F を用いた。これは下付きにした勾配作用を因子 F のみに対して施すことを意味する。
他には例えば、∇ ×(∇ × F) を考えれば、これはデカルト座標系で
となり、これを前の例で v → ∇ とした特別の場合として考えることができる。(この場合、 ∇2F は、問題のベクトルの各成分に対して個別にラプラス作用素を施したベクトルであることに注意)。
任意のスカラー場 ϕ に対し、その勾配の回転は常に零ベクトル、即ち
が成り立つ。また、ϕ がスカラー値で F がベクトル場ならば、
が成り立つ。
記述的な例[編集]
- 回転円板の各部の直線速度を記述するベクトル場において、回転は各点において同じ値を取る。
- 四つのマクスウェルの方程式のうちの二つ、ファラデーの法則とアンペールの法則は、回転を使って簡潔に書くことができる。ファラデーの法則は電場の回転が磁場の時間変化率のマイナス倍に等しいことを主唱するものであり、またアンペールの法則は磁場の回転が電流および電場の時間変化率に関係することを述べるものである。
一般化[編集]
ベクトル解析における演算 grad, curl, div を一般化することは、いくつかの段階を踏んで、微分形式の文脈で考えるのが最も容易に理解できる。簡単に言ってしまえば、各演算はそれぞれ順に、0-形式、1-形式、2-形式の微分に対応するのである。回転の幾何学的解釈は、三次元における二重ベクトル (2-ベクトル) の全体を無限小回転(座標をとれば 3 × 3 歪対称行列)の全体である特殊直交リー環 so(3) と同一視することに相当する。いっぽう、ベクトルによる回転の表現は、1-ベクトル(2-ベクトルで考えても同じだが)の全体を so(3) と同一視することに対応する(これらは何れも三次元空間になる)。
微分形式による定式化[編集]
三次元において、各係数は実函数であるものとして、
- 微分零次形式 (0-form) は、単なる函数 f(x, y, z)
- 微分一次形式 (1-form) は、一次結合
- 微分二次形式 (2-form) は、形式和
- 微分三次形式 (3-form) は、単項式
で与えられる。ここで、dx ∧ dy などの「楔積」は
などを満たし、ある種の有向(あるいは符号付き)面積として理解できる。R3 における k-形式の外微分は天下り式に (k+1)-形式として与えられ(これは Rn でも、例えば
に外微分 d を施したものが
で与えられ)、従って 1-形式の外微分は 2-形式、2-形式の外微分は 3-形式となる。一方、
など、混合微分の交換可能性 (interchangeability) が成り立つから、外微分を二度施したものは必ず 0 になる (d2 = 0)。
従って、k-形式全体の成す空間を Ωk(R3) と書くと、外微分 d によって系列
が得られる。ここで、空間 Ωk(Rn) は Rn 上のベクトル束である外積代数 の切断全体の成す空間に一致し、この外積代数の次元が二項係数 であるから、k > 3 または k < 0 のとき Ωk(R3) = 0 に注意して、次元のみ見ればパスカルの三角形の中の一行
- 0 → 1 → 3 → 3 → 1 → 0
が出てくる。一次元ファイバーが函数に対応し、三次元ファイバーがベクトル場に対応する(後述)。適当な同一視で割って、外微分から grad, curl, div に対応する三つの非自明な演算が導かれることに注意。
微分形式や微分は任意のユークリッド空間(あるいは実際は任意の多様体)の上でリーマン計量を使わずに定義することができるが、リーマン多様体(あるいはより一般の擬リーマン多様体)の上では、k-形式を k-ベクトル場と同一視することができる(k-形式は k-階共変ベクトルであり、擬リーマン計量がベクトルと共変ベクトルとの間の同型を与える)。また、「向き付けられた」ベクトル空間が非退化形式(ベクトルと共変ベクトルとの間の同型)を持つならば、k-ベクトルと (n − k)-ベクトルとの間に同型対応が存在し、特に向き付けられた擬リーマン多様体(の接空間)の上にそのような対応が入る。従って、向き付けられた擬リーマン多様体上では、k-形式、k-ベクトル場、(n − k)-形式、(n − k)-ベクトル場を互いに入れ替えるような操作が許される(ホッジ双対性と呼ばれる)。具体的に R3 上で考えると、
- 1-形式と 1-ベクトル場との交換
- 1-形式と 2-形式の交換
- dx, dy, dz は向きに注意してそれぞれ「双対」形式
- に対応する。従って一般に
以上から、0-形式と 3-形式は函数に、1-形式と 2-形式はベクトル場に対応し、
- grad は函数 (0-form) をベクトル場 (1-form) に、
- curl はベクトル場 (1-form) をベクトル場 (2-form) に、
- div はベクトル場 (2-form) を函数 (3-form) に
それぞれ写す演算として理解できる。一方、d2 = 0 なる事実に対応するのは、函数 f およびベクトル場 v に対する二つの恒等式 curl grad f = 0 および div curl v = 0 である。
grad と div に関しては上と同じ幾何学的解釈のもとでそのまま任意の向き付けられた擬リーマン多様体に対して一般化できる。これは、0-形式の空間と n-形式の空間が常に(ファイバーごとに)一次元でスカラー値函数の空間と同一視でき、かつ 1-形式の空間と (n − 1)-形式の空間が常に(ファイバーごとに)n-次元でベクトル場の空間と同一視できることによる。しかし、curl はこの方法で四次元やより高次元の場合へ(あるいは二次元やより低次元の場合へ)一般化することはできない。四次元の場合の微分形式の空間の次元は
- 0 → 1 → 4 → 6 → 4 → 1 → 0
であるから、(ファイバーごとに四次元な)1-ベクトル場の回転は、ファイバーごとに六次元な 2-ベクトル場
となり、これは確かに六つの線型独立な項を持つ和で、1-ベクトル場と同一視することはできない。また、d2 = 0 となることから、1-ベクトルを 2-ベクトルを経て 3-ベクトルへ写すことに意味を持たせることができない。従って、先の論法によってベクトル場をベクトル場へ写す回転作用素 curl を他の次元において得ることはできないことがわかる。
しかし、ベクトル場の回転を 2-ベクトル場として定義することは一般に可能である(後述)。
微分幾何学的な意味での回転[編集]
二重ベクトル(2-ベクトル)の集合は二次の外冪 に対応し、これは内積と座標系をとれば歪対称行列の全体であって、幾何学的には無限小回転全体の成す特殊直交リー環 so(V) と見做される。これは 次元であり、また無限小回転として 2-ベクトルを 1-ベクトル場の微分と解釈できるようになる。(自明な零次元の場合を除けば)三次元だけが を満たすから、この場合が最もすっきりと述べられ、よく用いられる。零次元と一次元では非自明な 2-ベクトルがないから、ベクトル場の回転は常に 0 である。二次元の場合、ベクトル場の回転はベクトル場ではなく、回転角によって与えられる函数(スカラー場)になってしまう(回転角には、時計回りと反時計回りの何れを正の向きとするかという「向き」が必要である)。これはスカラー場であるが、div とは別の場であり、特に両者は互いに直交することに注意。三次元の場合は、従前の通りベクトル場の回転はベクトル場になる。一方、四次元の場合のベクトル場の回転は、幾何学的には各点において六次元のリー環 so(4) の元が対応する。
二つの座標(例えば x と y)のみに依存する三次元ベクトル場の回転は、単なる(z-方向の)垂直ベクトル場で、その大きさが(本項で例に挙げた)二次元ベクトル場の回転によって与えられるものとなることに注意。
回転を二重ベクトル場(反対称二階テンソル)と考えることは、ベクトル解析とそれに関連する物理学を高次元化するのに用いられている[7]。
脚注[編集]
- ^ Proceedings of the London Mathematical Society, March 9th, 1871
- ^ Mathematical methods for physics and engineering, K.F. Riley, M.P. Hobson, S.J. Bence, Cambridge University Press, 2010, ISBN 978-0-521-86153-3
- ^ Vector Analysis (2nd Edition), M.R. Spiegel, S. Lipcshutz, D. Spellman, Schaum’s Outlines, McGraw Hill (USA), 2009, ISBN 978-0-07-161545-7
- ^ Gibbs, Josiah Willard; Wilson, Edwin Bidwell (1902), Vector analysis
- ^ Arfken, p. 43.
- ^ Weisstein, Eric W. "Curl". mathworld.wolfram.com (英語).
- ^ Generalizing Cross Products and Maxwell's Equations to Universal Extra Dimensions, A.W. McDavid, C.D. McMullen, 2006
参考文献[編集]
- Arfken, George B. and Hans J. Weber. Mathematical Methods For Physicists, Academic Press; 6 edition (June 21, 2005). ISBN 978-0-12-059876-2.
- Korn, Granino Arthur and Theresa M. Korn. Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review. New York: Dover Publications. pp. 157–160. ISBN 0-486-41147-8
関連項目[編集]
外部リンク[編集]
- Hazewinkel, Michiel, ed. (2001), “Curl”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- The idea of curl of a vector field
- Curl BetterExplained





![{\displaystyle \nabla \times {\boldsymbol {F}}={\begin{vmatrix}{\boldsymbol {i}}&{\boldsymbol {j}}&{\boldsymbol {k}}\\[5pt]{\dfrac {\partial }{\partial x}}&{\dfrac {\partial }{\partial y}}&{\dfrac {\partial }{\partial z}}\\[5pt]F_{x}&F_{y}&F_{z}\end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/383d2500e321a49630f20d525feb9ecc5b69e083)



![{\displaystyle \nabla \times {\boldsymbol {F}}={\bigl [}{\star }({\boldsymbol {d}}F^{\flat }){\bigr ]}^{\sharp }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec428b8da0e167c7cce28c0278362a2bcb20a911)




![{\displaystyle \nabla \times {\boldsymbol {F}}=0{\hat {\boldsymbol {x}}}+0{\hat {\boldsymbol {y}}}+\left[{\frac {\partial }{\partial x}}(-x)-{\frac {\partial }{\partial y}}y\right]{\hat {\boldsymbol {z}}}=-2{\hat {\boldsymbol {z}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d7072848ece4813cabcb0154bc5a6059503bf57)


![{\displaystyle \nabla \times ({\boldsymbol {v}}\times {\boldsymbol {F}})={\bigl [}(\nabla \cdot {\boldsymbol {F}})+{\boldsymbol {F}}\cdot \nabla {\bigr ]}{\boldsymbol {v}}-{\bigl [}(\nabla \cdot {\boldsymbol {v}})+{\boldsymbol {v}}\cdot \nabla {\bigr ]}{\boldsymbol {F}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34777e5617c9ab1905ba76e2ecca8a4d4f19aed7)




















