コンテンツにスキップ

リンク機構

出典: フリー百科事典『ウィキペディア（Wikipedia）』
（リンケージから転送）
4つの節と1つの自由度を持つプライヤの例。調整用のねじを考慮すれば5つの節と2つの自由度を持つ。

リンク機構（リンクきこう）とは複数のリンクを組み合わせて構成した機械機構のことである。

概要

[編集]

リンケージとは、リンクもしくは節と呼ばれる変形しない物体が、ジョイント（同様の意味で、対偶という用語が使われる場合もある）もしくは関節と呼ばれる可動部分により接続され、1つ以上の閉路を構成するものである。1つのリンクは複数のジョイントを持ち、ジョイントは様様な自由度で動く。リンケージが全体として可動なとき、つまり、1つのリンクに対して複数のリンクが可動なとき、そのリンケージを特にリンク機構と呼び、そうでないリンケージを構造物と呼ぶ。通常、リンク機構は入力を異なる出力に変える。その際に、動作、速度、加速度を変え、機械的倍率（英語版）を与える。

リンク機構を含む伝達機構全般を扱う学問を機構学という。

歴史

[編集]
流速制御用の遠心調速機。発電用水車が調速機を回転させ、調速機が水流を制御し、水流が発電用水車を駆動することで、調速機構を実現している。

リンク機構は機械の設計において基本的なものであるが、多くの単純なリンク機構は19世紀に入るまで発明されなかった。最も単純な棒を考えると、中心点の空間内での座標が3つ、回転方向を表す3つの座標(角度)で合計6つの自由度を持っている。岩と固定点に接するように配置された棒は、てことして岩を動かす動作をする。さらに、より多くのリンクを様々な方法で接続すると、それに応じて全体の動作が決まる。少数の部品により、非常に複雑で正確な動作をするリンク機構を作ることができる。

産業革命がリンク機構の黄金期であった。数学や、工学、工作技術の進歩が新しい機構を要求し、またそれを可能にした。現在では当たり前と思われている多くの単純なリンク機構が、この時代の英才の発明によるものである。レオンハルト・オイラー（Leonhard Euler）は、リンク機構の合成に関する研究を行った最初の数学者であり、ジェームズ・ワット（James Watt）は蒸気機関のピストンのためのワット・リンク（Watt linkage）を苦労して発明している。パフヌティ・チェビシェフ（Pafnuty Chebyshev）は、リンク機構について30年以上の研究を重ね、チェビシェフ多項式を生み出した。必要に応じて生み出された新しいリンク機構は、動力織機において力の変換や速度の制御に有用であった。スライドを用いずに正確な直線運動をする機構を発明するのにも数年を要した。

主にドイツ、ロシア、イギリスの科学者は、この領域を200年以上に渡って研究してきた。これにより今日では多くの古典的な研究や組み立ての問題（例えば2次元の動き）は解決されている（外部リンクを参照）。最近では、compliant structureが中心課題となっている。

今日では、機械的な計算機やタイプライター、ミシンなどのリンク機構の応用例の多くが電子技術に置き換えられた。しかし、現代のリンク機構の設計技術は進歩を続け、かつて技術者が数日がかりで設計していたものが、コンピュータにより数秒でできるようになっている。

デジタル制御によるサーボ機構が、一般的となって、一見扱いやすそうに感じられるかもしれないが、特定の動作に関する問題、特に速度と正確性が要求される場合は、いまだにリンク機構やカムによらなければ解決できない。

理論

[編集]

もっとも一般的なリンク機構は、1自由度を持っている。これは入力動作に対して単一の出力動作をするということである。ほとんどのリンク機構は2次元で、動作が1つの平面上に限定されている。空間的な（2次元ではない）リンク機構は、設計するのが難しいため、一般的ではない。

リンク機構の自由度を計算するには、クッツバッハ・グルーブラー方程式（Kutzbach-Gruebler's equation）を用いる。リンク機構の自由度の値は可動度（mobility）とも呼ばれる。

2次元でのリンク機構に対する簡素化したクッツバッハ・グルーブラー方程式は、以下の通りである。

= 可動度 = 自由度
= （地面のリンクを1つ含めた）リンクの数
= 1自由度の動作部の数（ピンやスライダージョイントの数）
Linkage mobility
Linkage mobility

2次元平面のより複雑なジョイントを含んだ場合のクッツバッハ・グルーブラー方程式は以下の通りである。

3次元の動作をする空間的なリンク要素に対しては以下の通りである。

= 可動度（自由度）
= （地面のリンクを1つ含めた）リンクの数
= （接続方法や自由度によらない）ジョイントの数
= 各ジョイントの自由度

油圧式動作の機械では、独立して制御される油圧シリンダーを数えることで自由度を容易に判定することができる。

複雑な動作を行える単純なリンク機構

一般的なジョイントの種類

[編集]
ピン
1自由度の回転ができる。軸受、ボルト継手、リベット、蝶番など。
スライダー
1または2自由度の直線運動。リニア軸受、油圧・水圧シリンダー、ローラー、ピストンなど。
ボールとソケット
3自由度。他のジョイントにより通常は1つの自由度に制限されている。

設計者は要求される出力動作、機械的倍率、速度と加速度からリンク機構を設計する。要求された性能を達成するために、リンク機構の種類が選択されて調整される。

各リンクはベクトルとして取り扱われ、リンクが1つのループを構成するのでそれらのベクトルは連立方程式として取り扱うことができる。機械的倍率やその他の重要な値も同様に取り扱える。動作の方程式は時間で微分することで構成要素の速度や加速度を得ることができる。

リンク機構の種類

[編集]

4つのリンクを持つ機構は、最も単純な閉路を持つ動的リンク機構である。この機構は2-3の単純な部品で複雑な動作をできる。コンピューター登場以前の過去には、より複雑な機構に比べると計算が容易であるために、とてもよく用いられていた。

4つのリンクを持つ機構の種類、s = 最短のリンク、l = 最長のリンク

その他の有名なリンク機構の種類。

おおむね放物線の動作をするリンク機構
  • パンタグラフ（4リンク、2自由度）
  • クランク・スライダー（4リンク、1自由度）
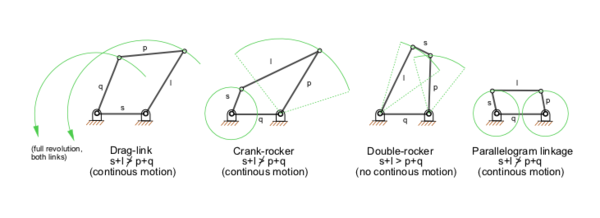
  • Grashof（4リンク、1自由度）最低1つのリンクが360度回転できる。
  • 5つのリンクを持つ機構はしばしば2つのリンクのかみ合いギア（1自由度）を持つ。4リンクの機構に比べて設計の自由度が高くよりすぐれた力の伝達を可能にする。
  • 6つのリンクと1つの自由度を持つ機構は、4つのリンクの機構に比べてより自由度の高い設計ができるが、多くの部品を必要とし設計が難しい。
    • ワット連鎖（Watt kinematic chain）
    • ワット1、2（Watt I, II）
    • スチーブンソン連鎖（Stephenson kinematic chain）
    • スチーブンソン1、2、3（Stephenson I, II, III）

並行・直線機構

[編集]


用途

[編集]
ジョイスティックに用いられる3自由度の空間リンク機構

リンク機構はもともと機械要素や道具に用いられていた。典型的な例はサスペンションやボルトカッターである。内燃機関のピストン、コンロッド、クランクは古典的な4リンク1自由度のリンク機構である。リンク機構は複雑な動作を実現する最も単純で安く効率的な方法として用いられている。

よく目にする例はワイパーである。4リンクのリンク機構で、モーターの回転運動を振動に変換している。ワイパーの中にはリンク機構をもう1つ備えてワイパーのブレードを正しい方向に向けるようになっているものもある。他によく見かけるものとしては、4リンクまたは6リンクのリンク機構を広範に使用した建設機械がある。

3次元のリンク機構はCADにより一般的なものとなった。

4リンクのリンク機構は、自転車に用いられている。通常のサスペンションを備えた自転車では、後輪がとても硬い弦のように動いて、上り坂で力をロスする。4リンクのリンク機構を備えた自転車では、大きな弦のように車輪が動いて、力のロスを30パーセント程度減らすことができる。

SKELETONICSは機械的なリンク機構のみで動作する外骨格である。

参考文献

[編集]
  1. Erdman, Arthur G.; Sandor, George N. (1984). Mechanism Design: Analysis and Synthesis. Prentice-Hall. ISBN 0-13-572396-5 
  2. How to Draw a Straight Line, historical discussion of linkage design （英語）
  3. What is a Watt I Linkage? （英語）

関連項目

[編集]

外部リンク

[編集]
ウィキメディア・コモンズには、リンク機構に関連するメディアがあります。
「https://ja.wikipedia.org/w/index.php?title=リンク機構&oldid=96723278」から取得