多項式函数 (初等数学)

初等数学における多項式函数（たこうしきかんすう、英: polynomial fucntion）または整函数 (function defined by integral expression) とは

${\begin{matrix}f_{k}\colon &\mathbb {R} &\to &\mathbb {R} \\&x&\mapsto &a_{k}x^{k}\end{matrix}}$

なる形の函数の和となっている函数を言う。この函数 f_k は次数 k のあるいは k-次の単項式函数と呼ぶ。すなわち、多項式函数は単項式函数の和である。

一般に、初等数学で扱う多項式函数は実数全体 ℝ 上で定義され ℝ に係数を持つが、場合によっては複素数全体 ℂ 上で定義され ℂ に係数をとる多項式函数を考えてもよい。これらの多項式函数は、定義域や係数を ℝ や ℂ 以外に取る一般の多項式函数の特別の場合になっている。

用語の濫用で、しばしば多項式函数のことを単に多項式と呼ぶので、多項式函数と形式多項式とが混同されがちである。初等数学の枠組みではこの混同はさほど問題とはならないが、一般の抽象代数学では誤った理解につながりかねないので注意すべきである。

例

次数が5の関数の例

記法の混乱を避けるため、以下で扱う多項式函数の定義域は常に $\mathbb {R}$または $\mathbb {C}$ とする。

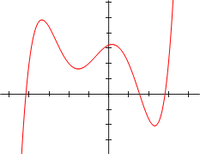
• $f:x\mapsto x^{5}+6\cdot x^{3}+3\cdot x^{2}-{\sqrt {2}}\cdot x+3$ は次数 5 の多項式函数である。
• 零多項式を除く多項式函数の次数とは、その最も高い次数の単項式函数の次数のこととする。零でない定数函数は次数零の単項式函数である。零定数函数は次数 $-\infty$ の多項式函数と見なされる。
• 一次函数は $f(x):=ax+b(a\neq 0)$ で定義され、一次二項式函数である。同様に $f(x):=ax^{2}+bx+c(a\neq 0)$ と定義される函数は二次三項式函数である。

多項式の根

詳細は「多項式の根」を参照

多項式 f に対し、f(r) = 0 を満たす定数 r は多項式 f の根と呼ばれる。このとき、f は一次二項式 x − r で割り切れることが示せる（因数定理）。

一次二項式

f(x) = ax + b (a ≠ 0)

根 r ≔ −b/a

因数分解系: f(x) = a(x − r)

二次三項式

詳細は「二次方程式」を参照

二次多項式函数は、ℝ 上では判別式の符号にしたがって零個または二個（二つは一致してもよい）の根を持つが、ℂ 上では常に二つの根を持つ。

二個の根を持てば、因数分解: f(x) = a(x − r₁)(x − r₂) が可能。

一般の場合

初等数学においては、二次以上の多項式函数の求根は「明らかな」根を持つ場合に限られる。

• 例えば f(x) = x³ + 3x² − 16x + 12 は、ほかの単純な値の中でも f(2) を計算することにより、2 が f の根となることが確かめられる。因数分解は、ホーナー法や多項式の除法、係数比較など様々な方法で行える。

多項式の決定

ℝ または ℂ 上定義された n 次多項式函数が、n より大きな回数 0 になることはないことが示せる。したがって、次数が高々 n の二つの多項式が、n 個より多くの点で一致しているならば、両者が恒等的に一致（次数が等しくかつすべての係数も等しい）していなければならない。これを「多項式の決定」(identification; 同定) あるいは係数比較という。

これは特定の式に対するより良い近似式を見つける方法を与える効果的な性質である。

例 1

全ての実数 x に対し x³ + 3x² − 16x + 12 = (x − 2)(x² + ax + b) となる a, b を求めよ

f(x) ≔ x³ + 3x² − 16x + 12,

g(x) ≔ (x − 2)(x² + ax + b)

とおいて g(x) を展開する: g(x) = x³ + (a − 2)x² + (b − 2a)x − 2b.

二つの多項式函数は三点以上で一致しているから恒等的に等しくなり、ともに同じ次数 3 を持ち、すべての次数の係数がそれぞれ等しい。言葉を変えれば、すべての x において f(x) = g(x) となるための必要十分条件は

$${\begin{cases}1=1\\3=a-2\\-16=b-2a\\12=-2b\end{cases}}\iff {\begin{cases}a=5\\b=-6\end{cases}}.$$

したがって、f(x) = (x − 2)(x² + 5x − 6) を得る。

例 2

f(x) = x⁴ − 4x³ + 9x² − 10x − 1 で定義される多項式函数のグラフが方程式 x = 1 で表される直線を軸とする対称性を持つことに注意する。すべての実数 x に対して f(x) = (x − 1)⁴ + a(x − 1)² + b を満たす二つの実数 a, b を求めよ。

g(x) ≔ (x − 1)⁴ + a(x − 1)² + b

とおき、g(x) をよく知られた公式（二項定理）によって展開する:

g(x) = x⁴ − 4x³ + (6 + a)x² − (4 + 2a)x + 1 + a + b,

よって係数比較:

$${\begin{cases}1=1\\-4=-4\\9=6+a\\10=4+2a\\-1=1+a+b\end{cases}}\iff {\begin{cases}a=3\\b=-5\end{cases}}$$

により f(x) = (x − 1)⁴ + 3(x − 1)² − 5 を得る。

例 3

x ≠ 2 で定義された有理函数 f(x) ≔ 2x² + 3x − 5/x − 2 を簡約形にせよ。すなわち、任意の x ≠ 2 に対して f(x) = ax + b + c/x − 2 を満たす実数 a, b, c を求めよ。

g(x) ≔ ax + b + c/x − 2

とおいて通分すれば g(x) = ax² + (b − 2a)x + c − 2b/x − 2.

二つの函数 f, g は分母が等しいから、両者が x ≠ 2 で一致するための必要十分条件は、両者の分子が x ≠ 2 で一致することである。これらの分子はともに二次の多項式で二点以上で一致しているから、両者の係数比較

$${\begin{cases}2=a\\3=b-2a\\-5=c-2b\end{cases}}\iff {\begin{cases}a=2\\b=7\\c=9\end{cases}}$$

により f(x) = 2x + 7 + 9/x − 2 を得る。

対称性の要素

多項式函数 f のグラフが y-軸 Oy を対象の軸に持つための必要十分条件は、f に現れるすべての単項式の次数が偶数となることである。おそらくこの性質が、グラフが Oy を対称の軸にもつ任意の函数を偶函数と呼ぶ由来である。

同様に、多項式函数 f が原点 O を対称の中心に持つための必要十分条件は、f に現れるすべての単項式の次数が奇数となることである。奇函数を参照。

初等解析学

一次函数および二次函数の解析学的性質はよく知られている。より高次の多項式函数についても、いくつか知られた事実がある。

ℝ 上定義された多項式函数は ℝ の各点で微分可能である。正整数 k に対し、単項式 f_k(x) ≔ a_k⋅x^k の導函数は f′(x) = k⋅a_kx^k−1 で与えられる。定数単項式の導函数は零函数である。

• したがって特に、ℝ 上定義された多項式函数は ℝ 上の各点で連続である。

多項式函数の無限遠への極限は、そのもとも高い次数の単項式の極限に一致する。

• a_nxⁿ の +∞ への極限は
  • a_n > 0 ならば +∞;
  • a_n < 0 ならば −∞.
• a_nxⁿ の −∞ への極限は
  • a_n > 0 かつ n が偶数ならば +∞;
  • a_n > 0 かつ n が奇数ならば −∞;
  • a_n < 0 かつ n が偶数ならば −∞;
  • a_n < 0 かつ n が奇数ならば +∞.

いくつかの話題への導入

初等数学の範疇には三次多項式の根を求めるカルダノの公式も四次方程式の根に対するそれも含まれていない。そのような方法の存在は五次より大きな多項式の求根に対する一般公式の存在をにおわせるが、実はそのようなものはないのである。

詳細は「多項式の歴史」を参照

二次多項式に対する根の存在は「ℂ に係数をとる n-次の多項式が（重複度まで込めて）n 個の根を ℂ に持つ」ことを述べた代数学の基本定理に対する最初の入り口である。