逆2乗の法則
逆2乗の法則(ぎゃくにじょうのほうそく、英: inverse square law)とは、物理量の大きさがその発生源からの距離の2乗に反比例するという法則である。
逆2乗とは2乗の逆数のことであり、この法則はしばしば、ある物理量の大きさがその発生源からの距離の逆2乗に比例する、という形でも述べられる。逆2乗の法則はしばしば短縮して逆2乗則とも呼ばれる。
逆2乗の法則は冪乗則の一種であり、様々な物理現象の中に見出すことができる。以下の節では自然科学と物理学の歴史の中で特に重要な例について述べる。逆2乗の法則の発見により、物理学者は何らかの変化を認めたとき、その発生源と発生源との距離の関係を調べ、それらが逆2乗の法則に当てはまるかどうかに関心を持つようになった。
逆2乗の法則が成り立つこと、特に指数が 2 であることには、我々のいる空間が3次元であり等方的であることと密接に関係している。空間の各点で測定できる物理量について、それがある発生源から生じる流体のようなものと見なせる場合、発生源から偏りなく流出する物質からの類推により、発生源を囲む球面を通過する物質の量は、球面の大きさによらず一定であると考えることができる。したがって球面を通過する物質の密度は球面の面積に反比例して小さくなる。発生源が球殻の中心にあるとすれば、球面の大きさは発生源から球面までの距離の2乗に比例するから、球面を通過する物質の密度は球面と発生源の距離の2乗に反比例する。
逆2乗の法則が成り立つことは、発生源の形状に強く依存している。逆2乗の法則が成り立つのは発生源が点や真球と見なせる場合であり、例えば棒状の光源に対しては逆2乗の法則は成り立たない。一般には、発生源の細かな構造を無視できる程度の距離においてのみ、より具体的には発生源の大きさに比べて非常に遠距離の領域で逆2乗の法則が成り立つ。
逆2乗の法則が成り立つのは大抵、ある一つの発生源に注目した場合である。たとえば異なる天体の表面重力を比較する際には注意が必要である。構成物質の似通った天体同士では表面重力の大きさは天体の半径に対する逆2乗則に従わず、自転による遠心力の影響を除けば、表面重力の大きさは半径に概ね比例する。これは、重力の大きさが天体の質量に比例し、同程度の密度を持つ天体の質量を比較すると、天体の質量は天体の体積に比例するためである。
光の減衰の法則[編集]
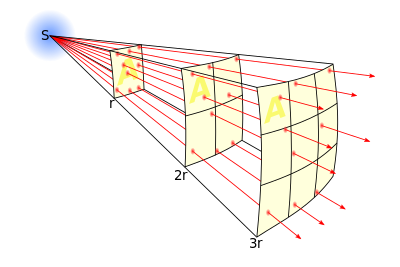
光の減衰に関する逆2乗の法則は、光の強さが光源からの距離の2乗に反比例することを述べる。これは初期に発見された逆2乗の法則の一つである。証明の概略は次のとおり。
- 光源からの距離が一定である球面を想定する。光源から出た光は直進する(ユークリッドの光の直進の法則)ため、すべてがこの球面を通過する。つまりどんな直径の球面を想定しても、その球面を通過する光の量は等しい。一方で球の表面積は半径の 2 乗に比例するので、光の強さは光源からの距離の2乗に反比例する。
ヨハネス・ケプラーは、1596年に発表した著作『宇宙の神秘』の中で、平面上に等方的に光が放出される場合について上記の考察と同様の議論をした。ケプラーはまた、天体に及ぼされる引力についても同様の考えが成り立つと推察し、重力に関する理論を展開した[1]。ケプラーは重力の広がりを球面ではなく円によって捉えたがために逆2乗の法則を導くことはなかった[2]。ケプラーが、天体を動かす原動力が同心円状に広がると考えたのは、当時知られていた惑星の軌道がほぼ同一平面状にあったためである(当時は彗星の軌道は計算されていなかった)。
万有引力の法則[編集]
万有引力の法則は逆2乗の法則の中でもよく知られている。引力に関する逆 2 乗則の発見者としてロバート・フックとアイザック・ニュートンは特に有名である。フックとニュートンはケプラーの考え方を拡張し、またニュートンはフックの示唆もあって「万有引力は全方位に影響を与え、その強さは距離の 2 乗に反比例する」と考えた。1680年にフックはこの法則について述べた書簡をニュートンに送っている[3]。万有引力について満足いく結果が得られたのはニュートンが著した『自然哲学の数学的諸原理』においてであり、その初版は1687年に出版されている[4]。
ニュートンは『自然哲学の数学的諸原理』を出す以前に微分積分学の基本定理を証明し、微分積分学を創始するに至っているが、『自然哲学の数学的諸原理』ではそれらの結果を放棄し、あるいは露わにはしていない[5]。ニュートンの時代にはまだ微分積分学で用いられる無限小の代数は正統的な手法とは見なされておらず、ニュートンは幾何学の手法によって力学の基本法則やそこから導かれる定理を説明した。
クーロンの法則[編集]
電磁気学における逆2乗の法則として、クーロンの法則がある。クーロンの法則は、発見者のシャルル・ド・クーロンから名前が取られている。クーロンの法則には電場に対するものと磁場に対するものの2種類ある。前者は球形または点状の電荷が作る電場の強さを述べたもので、後者は双極子の一方の極が作る磁場の強さを述べたものである。
クーロンの法則は、近接作用論の立場では電磁場に関する法則として述べられるが、ニュートンの万有引力のように2つの物体の間に働く力として表すこともできる。この場合、電場に関するクーロンの法則は「電荷を持つ粒子同士に働く静電気力の大きさは、粒子間の距離の逆2乗に比例する」と表現できる。クーロン自身はねじれ秤を用いて2つの帯電した物体の間に働く力を測定することによって、静電気力に関するクーロンの法則を発見している[6]。
磁場に関するクーロンの法則は、磁場に関するガウスの法則により磁場の湧出がゼロでない発生源が存在しないため[7]、直接的には成り立たない。磁場についてクーロンの法則が成り立つためには、磁気単極子(モノポール)という概念が必要となる。前述の通り、ガウスの法則から磁場の湧出はゼロとなるため、磁気単極子は単体では存在し得ないが、微小な円電流のなす磁場を磁気双極子(ダイポール)のなす磁場と見なすことができ、磁気双極子を構成する粒子として磁気単極子を扱うことができる[8]。
出典[編集]
参考文献[編集]
- 山本, 義隆『磁気と重力の発見 3 近代の始まり』みすず書房、2003年5月22日、605–947頁頁。ISBN 4-622-08033-8。
- 砂川, 重信『電磁気学』(新装版)岩波書店〈物理テキストシリーズ 4〉、1987年1月29日。ISBN 4-00-007744-9。
関連項目[編集]
- ガウスの法則
- 発散 (ベクトル解析)
- 斉次関数(同次関数)
