自然放出
自然放出(しぜんほうしゅつ、英語:spontaneous emission)とは、光の放出(発光)の一種であり、誘導放出とは区別される。
- 光の放出とは、光源となる物質 (原子、分子、原子核など) が励起状態からよりエネルギーの低い量子状態 (たとえば基底状態) へ移り、その際に光子を放出する過程のことである(光の吸収の時間反転の過程)。自然放出と誘導放出との和である。
自然放出が誘導放出と区別される点は、自発的に励起状態から別のエネルギー状態への遷移が起こることであり、したがって外部から入力される光の強さに依存しない[1]。
量子化された電磁波 (つまり調和振動子の集まり) の零点振動に誘起されるものが自然放出である。理論的に量子化された光を用いることで吸収および放出(自然放出+誘導放出)を正しく記述できる[2]。
多くの発光の現象は自然放出である(レーザーなどの発光を除く)[3]。
導入[編集]
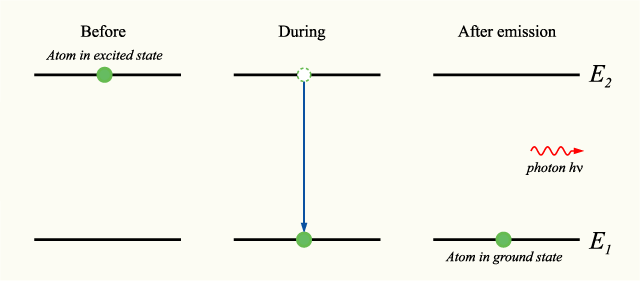
光源として原子を考える。原子は、エネルギー準位が E2 の励起状態から、より低いエネルギー準位 E1 の状態に自発的に遷移し、そのとき、二つの状態のエネルギーの差分に等しいエネルギーを持つ光子を放出するとする。光子のエネルギーは振動数 (周波数) ν とプランク定数 h の積 hν (あるいは角振動数 ω = 2πν と換算プランク定数 ℏ = h/2π を用いて、ℏω) で表され、放出される光子の、振動数とエネルギーの関係は、
となる。 自然放出では、誘導放出と異なり、放出される光子の位相や放出される方向はランダムである。 自然放出の過程とエネルギー準位を示した図を以下に示す。
励起状態の原子の個数を N で表すと、励起原子一つ一つが各時刻に一定の確率で遷移するとして、単位時間あたりに減少する励起原子の数は、励起原子の個数に比例するから、
となる。ここで A2,1 は一つの励起原子に対する自然放出の頻度である (単位は [時間]-1)。 比例定数 A2,1 は光源となる原子によって決まり、これはアインシュタインの A 係数 (Einstein A coefficient) と呼ばれる[4]。
上に示した方程式は一般解を求めることができて、初期条件を与えた解は次のようになる。
ここで N (0) は最初にあった励起原子の数であり、Γrad は放射の減衰速度を表す。
励起原子の数 N は、原子核の放射性崩壊と同様に、指数関数的に減衰していく。 Γradτ2,1 = 1 となるまでの時間 τ2,1 を寿命 (lifetime) と呼び、このとき励起原子の数は元の数のおよそ 36.8% (e-1) に減衰している。その後も一つの寿命を過ぎるごとに、励起原子の数は 36.8% にされていく。 放射減衰速度 Γrad とアインシュタインの係数 A2,1、励起原子の寿命 τ2,1 の関係は以下の通り。
理論[編集]
自然放出は、電磁場を量子化しない、半古典的な量子論の枠組みでは説明することができない。 実際、量子力学の中で定常状態から他の定常状態へ遷移する確率を計算すると、その確率はゼロであることが示される。 そのため、自然放出を説明するには、量子力学を場の量子論へ拡張し、電磁場を空間の各点について量子化して取り扱わなければならない。この電子と電磁場に関する場の量子論は、量子電磁力学として知られる。
量子電磁力学 (QED) では、電磁場には基底状態すなわち真空状態があって、系全体の状態は励起原子と電磁場を合わせた形で記述される(詳細には文献 [2] を参照)。電磁場と原子との相互作用を考えることで、通常の量子力学において「定常状態」であった原子は固有状態ではなくなり、安定に存在できなくなる。特に、電子が励起状態から基底状態へと遷移すると、電磁場が基底状態から励起状態へと遷移し、一つの光子が場に生成される。自由空間における自然放出は真空のゆらぎ (vacuum fluctuations) から生じる[5][6]。
脚注[編集]
- ^ これに対して誘導放出の強さは、外部から入力される光の強さに依存し比例する。
- ^ 半古典論による取り扱いでは自然放出は記述できず、誘導放出しか理論に現れない。
- ^ 多くの自然現象で重要な役割を果たし、応用面においても、蛍光灯や、テレビなどのモニターに用いられるブラウン管、プラズマディスプレイ、発光ダイオード (LED) などに利用されている。
- ^ R. Loudon, The Quantum Theory of Light, 3rd ed. (Oxford University Press Inc.,New York, 2001).
- ^ Hiroyuki Yokoyama & Ujihara K (1995). Spontaneous emission and laser oscillation in microcavities. Boca Raton: CRC Press. p. 6. ISBN 0-8493-3786-0
- ^ Marian O Scully & M. Suhail Zubairy (1997). Quantum optics. Cambridge UK: Cambridge University Press. p. §1.5.2 pp. 22–23. ISBN 0-521-43595-1