反転幾何学
初等幾何学における反転幾何学(はんてんきかがく、英: inversive geometry)は、平面幾何学において反転 (inversion) と呼ばれる種類の変換を一般化したものに関して保たれる図形の性質について研究する。
平面上の反転変換は、角を保ち(等角性)、一般化された円を一般化された円に写す(「円円対応」)ような写像になっている。ここで「一般化された円」というのは、円または(無限遠点を中心とする半径無限大の円と見做される)直線のいずれかであることを意味する。初等幾何学における難しい問題が、反転を施すと扱いやすくなるというようなことも少なくない。
このような平面上の反転の概念を、より高次元の場合に一般化することができる。
円に関する反転[編集]
点の反転[編集]
-
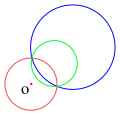
点 P′ は点 P を赤い円に関して反転した点である。
-
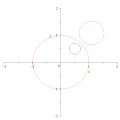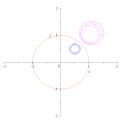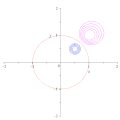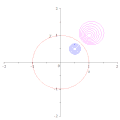
点 O を通る円(青)の、赤い円に関する反転は、点 O を通らない直線(緑)になる。逆もまた然り。
-
点 O を通らない円(青)の、赤い円に関する反転は、点 O を通らない円(緑)になり、逆もまた然り。
-
円 O の外側にある点 P の、反転点 P′ の作図方法。円 O の半径を r として、直角三角形 OPN, OP′N は相似ゆえ、OP : r は r : OP′ に等しい。
-
円に関する反転では、円の中心が写る先の円の中心へ写るわけではない。
平面において、中心 O, 半径 r の基準円 (reference circle) に関して点 P を反転すると、O を始点として P を通る半直線上で
を満たす点 P′ に写る。反転変換によって O と異なる各点 P がその像 P′ へ写るとき、それと同時に点 P′ は P に写される。故に、同じ反転変換を二度続けて施した結果として得られる変換は、O を除く平面上の点全体の成す集合上では恒等変換になる。反転変換を対合とするためには、平面上の全ての直線上に載っている唯一の点として無限遠点を導入し、反転の定義域を拡張して、基準円の中心 O と無限遠点とが入れ替わるようにしなければならない。
定義から従うことに、基準円の内側にある各点は基準円の外側へ、外側の各点は内側へそれぞれ写り、中心と無限遠点とが入れ替わる一方、基準円の周上にある各点は何ら影響も受けない。端的に言えば、円の中心に近ければ近いほど反転変換で遠くに写り、遠ければ遠いほど近くへ写るということである。
性質[編集]
平面上の点集合の反転は、それを基準円で分離したときのそれぞれの部分を反転して得られる点集合になる。円反転に関して以下の性質は重要である。
- 基準円の中心を通る円は、基準円の中心を通らない直線に反転し、逆に基準円の中心を通らない直線は基準円の中心を通る円に反転する。一方、基準円の中心を通る直線は、反転して自分自身に写る。
- 基準円の中心を通らない円を反転すると、円と基準点の交点は変わらずやはり基準円の中心を通らない円に写る。円(または直線)が反転変換で保たれるための必要十分条件は、それが基準円との交点において基準円と直交することである。
他には以下のような性質がある:
- 相異なる二点 A, A′ を通る円 q の、円 k に関する反転が A, A′ を入れ替えるならば、二円 k, q は互いに直交する。
- 二円 k, q が直交するとき、k の中心 O を通り q と交わる直線は、従って q との交点の k に関する反転点でも交わる。
- 円 k の中心 O を一つの頂点とする三角形 OAB を取り、A および B の k に関する反転点をそれぞれ A′ および B′ とすれば、が成り立つ。
- 基準円 k に直交する二円 p, q の二交点は、k に関する反転によって互いに入れ替わる。
- 二点 M, M′ が互いに基準円 k に関する反転点で、それぞれ曲線 m, m′ 上に載っていて、曲線 m, m′ も k に関する反転で互いに入れ替わるとすると、曲線 m および m′ の点 M および M′ における接線は、直線 MM′ に直交するか、さもなくば線分 MM′ を底辺とする二等辺三角形を成す。
- 反転変換によって角の大きさはそのまま保たれるが、有向角の向きは逆になる。
応用[編集]
ある円の中心、その円を円反転して得られる円の中心、基準円の中心は共線関係を持つ(同一直線上にある)ことに注意する。この事実は、三角形の内接三角形のオイラー線が、その内心 I と外心 O を通る直線 OI に一致することを示すのに有用である。
三角形 ABC の内接円に関する反転変換で、内接三角形の中点三角形は三角形 ABC に写る。これはつまり、中点三角形の外心は内接三角形の九点心であって、三角形 ABC の内心および外心と共線であることを意味する。
交わりを持たない任意の二円は同心円に反転され得る、その場合それらの円の間の反転距離 δ は、同心な二円の半径の比の自然対数として定義される。
加えて、交わりを持たない任意の二円は、反相似円上の点を中心とする円に関する反転で、合同な二円に写すことができる。
ポースリエリンク機構は円反転の機械的実装である。これを使えば、直線運動と円運動との変換という重要な問題の厳密な解が得られる。
三次元内の反転[編集]
円反転は、三次元空間における球面反転に一般化される。空間内の点 P の、中心 O, 半径 R の基準球面に関する反転点を P′ とすると、
かつ、二点 P, P′ は O を始点とする一つの半直線上にある。二次元の場合と同様に、球面反転によって球面は球面に写る(ただし、球面が基準球面の中心 O を通る場合は例外で、この場合は平面に写る)。基準円の中心 O を通らない任意の平面は、反転して O に接する球面に写る。球面と割平面との交点としての円は、同じく円に写るが、やはり例外として円が基準球面の中心 O を通る場合には直線に写る。このことは、割平面が基準球面の中心 O を通る場合には二次元の場合に帰着できるが、通らない場合には三次元特有の現象である。
球面反転の特別の場合として立体射影がある。半径 1 の球面 B と、B の南極 S で B に接する平面 P を考えると、平面 P は球面 B の、北極 N に関する立体射影である。ここで、B の北極 N を中心とする半径 2 の球面 B2 を考えると、B2 に関する反転で 球面 B はその立体射影 P に写される。
公理化と一般化[編集]
ユークリッド平面あるいはより一般に任意のアフィン平面に、ただ一つの無限遠点を各直線に対して追加したものを考えることによって得られるのがメビウス平面あるいは反転平面 (inversive plane) と呼ばれるものである。これらメビウス平面は公理的に記述することができるものであって、有限幾何も無限幾何も両方が存在する。
ユークリッド平面から構成できるメビウス平面の一つの模型がリーマン球面である。
エルランゲン目録との関係[編集]
コクセター (2009, pp. 155–187, 6 円と球) に従えば、円に関する反転変換は1831年にマグヌスが考案し、それ以来この写像は高等数学における手段の一つとなった[1]。円反転変換はいくつかの段階を経て応用されていき、じきに変換幾何学を学ぶ者がクラインのエルランゲン目録の重要性を認め、副産物として双曲幾何学のある種の模型が得られた。
拡縮変換[編集]
同心円に関する二つの反転変換の合成は、それらの円の半径同士の比によって特徴付けられる中心相似変換(similarity, homothety) あるいは拡大縮小 (dilation) などと呼ばれるものになる。実際に式で書けば、二円の半径を変換を施す順に R, T として
は (T/R)2-倍変換である。
逆数変換[編集]
平面上の点を複素数 z = x + iy と解釈し、複素共軛 z = x − iy も考えれば、z の逆数は
で与えられるから、帰結として単位円に関する反転 z ↦ w は、代数的な形で
と書くことができる。逆数変換 (reciprocation) はメビウス群の生成元として、変換論で重要である。メビウス群の他の生成元は、平行移動と回転で、何れも三次元空間全体において物理的な操作を通してよく知られているものである。(上記円反転に依存した)逆数変換の導入は、(ユークリッド平面の反転幾何と同一視されることもある)メビウス幾何に固有の特性 (peculiar nature) を与えるものであるけれども、しかし反転幾何は(共軛を含めて逆数変換にしていない)生の円反転を含むから、メビウス幾何よりも広汎な研究領域である。反転幾何は共軛写像も含むが、共軛写像も円反転も非等角的である(後述)から、これらは何れもメビウス群の元ではない。メビウス群の元は、数平面全体で定義された解析函数であり、従って等角写像でなければならない。
より高度な幾何学へ[編集]
既に述べたとおり、原点(あるいは 0)は円反転写像において特別な注意を要し、∞ または 1/0 で示される無限遠点が添加される。複素数を用いた方法では、逆数変換がはっきりした演算として表され、無限遠点の添加によってリーマン球面としばしば呼ばれる複素射影直線の概念が導かれる。この空間およびその上の変換群の、部分空間及び部分群は、ベルトラミ、ケイリー、クラインらによって双曲幾何の初期の模型を導入するのに利用された。そして、これらの平面幾何におけるロバチェフスキーおよびボヤイに端を発する様々なアイデアを反転幾何は含んでいる。さらにクラインは1872年に発表したエルランゲン目録と言われる声明で、この変換写像群と幾何学的現象とを同一視することにより、大きく事態を打開する。それ以降、多くの数学者は空間にその上の変換写像からなる群を合わせて考えたものに対して「幾何(学)」(geometry) の語を用いるようになった。この意味での幾何学における図形の有意な性質とは、この変換群に関する不変量 (invariant) のことである。
例えば、スモゴルチェフスキーはロバチェフスキー幾何学の創始以前に反転幾何学の様々な定理を展開している[2]。
高次元での反転[編集]
高次元へ一般化された意味において、反転幾何学とはユークリッド空間上の運動(等距変換)全体と n-次元球面に関する反転変換
(r は反転の基準球面の半径)とで生成される変換群の研究のことである。
上記の反転を二次元で r = 1 として考えたものは、単位円に関する円反転に他ならない。
既に述べたことと同様、反転幾何学では直線と円(あるいは超平面と超球面)とに区別がなく、ユークリッド幾何に無限遠点を添加したものへ特定の埋め込みを考えれば、直線は単純に一つの円であって、その幾何の中で円を別の円に写したりすることを考えることができる。
高次元の共形写像が n-次元球面または超平面に関する反転とユークリッドの運動から厳密に生じるということは、著しい事実である(等角写像に関するリウヴィルの定理を参照)。
反等角性[編集]
円反転写像は反等角(反共形)、つまり各点において反転は角を保ち、かつ向きを逆にする(等角写像(共形写像)の場合であれば、「向き付けられた」角を保つ)。代数的には、写像が反共形になるのは、各点においてヤコビ行列が行列式の値が負の直交行列のスカラー倍になっている場合に限る(二次元の場合で言えば、ヤコビ行列が各点で鏡映のスカラー倍にならないといけないということ)。式で書けば、ヤコビ行列を J として、J⋅tJ = kI(k は適当なスカラー、I は単位行列)かつ det(J) = −√k と書ける場合ということである。zi = xi/‖ x ‖2 —ただし ‖ x ‖2 ≔ x 2
1 + ⋯ + x 2
n — の場合にヤコビ行列を計算すれば、JJ⊤ = kI (k ≔ 1/‖ x ‖4) となり、det(J) が負となることも計算すればわかるから、この反転が反等角であることが確かめられる。
複素数平面において、最も分かり易い円反転写像(つまり原点中心の単位円に関するもの)は、各点 z を 1/z へ写す複素反転写像の複素共軛に等しい。複素解析的反転写像は等角であり、その共軛である円反転は反等角であるということになる。
反転と双曲幾何[編集]
は、a 2
1 + ⋯ + a 2
n > c なる限り正の半径を持ち、反転によって球面
に写る。従って、先の球面が反転に関して不変となることと、c = 1 は同値となる。しかしこれは単位球面に対する直交条件であって、従って反転不変 (n − 1)-次元球面
は、単位球面と直交し、かつ単位球面の外側に中心を持つ。このような球面とその部分空間としてそれらを半球面に分離する超平面を合わせて考えたものは、双曲幾何学のポワンカレ円板模型に関する超曲面である。
単位球面に関する反転はそれに直交する球面を不変にするから、反転変換写像は単位円の内側の点を外側へ、外側の点を内側へ写す。従って、このことは一般の直交球面において成り立つのであって、特に単位球面に直交する一つの球面に関する反転は、単位球面を単位球面自身に、かつ単位球面の内部の点を単位球面の内部に写すとともに、直交球面の内側の点を外側へ写し、かつ外側の点を内側へ写すから、この反転変換によりポワンカレ円板模型の鏡映変換が(単位球面の分離半球の直径を通る鏡映も含めるならば)定まる。こうして得られる鏡映変換の全体は、円板模型の等距変換群を生成する、つまりこの模型上の等距変換は等角写像である。従って、この模型内の二曲線のなす角は双曲空間において二曲線の成す角と等しい。
注[編集]
注釈[編集]
出典[編集]
- ^ Coxeter 1969, pp. 77–95, Chapter 6: Circles and Spheres.
- ^ A.S. Smogorzhevsky (1982) Lobachevskian Geometry, Mir Publishers, Moscow
関連項目[編集]
参考文献[編集]
- Blair, David E. (2000), Inversion Theory and Conformal Mapping, American Mathematical Society, ISBN 0-8218-2636-0
- Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (2011), “Chapter 5: Inversive Geometry”, Geometry (2nd ed.), Cambridge: Cambridge University Press, pp. 261–342, ISBN 978-1-107-64783-1
- Hartshorne, Robin (2000), “Chapter 7: Non-Euclidean Geometry, Section 37: Circular Inversion”, Geometry: Euclid and Beyond, Springer, ISBN 0-387-98650-2
- ハーツホーンR.「37 円に関する反転」『幾何学 現代数学から見たユークリッド原論』 II、難波誠訳、丸善出版、2008年2月9日。ISBN 978-4-621-06312-5。
- Coxeter, H.S.M. (1969) [1961], “6 CIRCLES AND SPHERES”, Introduction to Geometry (2nd ed.), John Wiley & Sons, pp. 77–95, ISBN 0-471-18283-4
- コクセターH.S.M.「6 円と球」『幾何学入門』 上、銀林浩訳、筑摩書房〈ちくま学芸文庫〉、2009年9月10日、155-187頁。ISBN 978-4-480-09241-0。
外部リンク[編集]
- 立花俊一『反転』 - コトバンク
- Inversion: Reflection in a Circle at cut-the-knot
- Wilson Stother's inversive geometry page
- IMO Compendium Training Materials practice problems on how to use inversion for math olympiad problems
- Weisstein, Eric W. "Inversion". mathworld.wolfram.com (英語).
- Visual Dictionary of Special Plane Curves Xah Lee