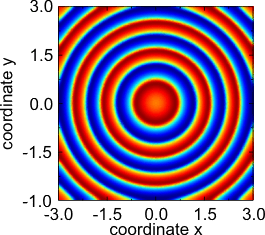
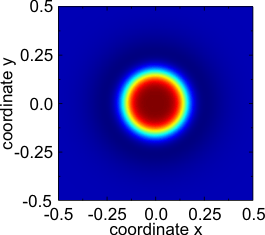
反応拡散系

反応拡散系(はんのうかくさんけい、英: reaction-diffusion system)とは、空間に分布された一種あるいは複数種の物質の濃度が、物質がお互いに変化し合うような局所的な化学反応と、空間全体に物質が広がる拡散の、二つのプロセスの影響によって変化する様子を数理モデル化したものである。
概要[編集]
反応拡散系は、化学の分野において自然な形で応用されるものである。しかし、化学的ではない動力学過程を表現する上でも、反応拡散系は応用される。例えば、生物学や地質学、物理学や生態学において、そのような応用例は見られる。数学的に言うと、反応拡散系は半線形放物型偏微分方程式の形を取るものである。
一般的には次のように記述される。
ここでベクトル q(x,t) の各成分はある物質の濃度を表し、 は拡散係数からなる対角行列を表し、R はすべての局所的な反応を表す。反応拡散方程式の解は、進行波の形成や波に似た現象、あるいは帯や六角形のような自己組織パターン、あるいは散逸ソリトンのようなより複雑な構造を含む、幅広い範囲の挙動を見せるものである。
一成分の反応拡散方程式[編集]
最も簡単な反応拡散方程式は、空間一次元における単一物質の濃度 u に関するもので、
と記述され、これはKPP方程式(Kolmogorov-Petrovsky-Piskounov の略)とも呼ばれる[1]。反応項が無い場合、方程式は純粋な拡散過程のみを表す。そのような方程式はフィックの第二法則に関係するものである。反応項が R(u) = u(1-u) である場合、生物学的な人口の広がりを表現するために元々用いられた、フィッシャーの方程式が得られる[2]。R(u) = u(1 − u2) である場合、レイリー=ベナール対流を表すためのニューウェル=ホワイトヘッド=シーゲル方程式が得られる[3][4]。R(u) = u(1 − u)(u − α) および 0 < α < 1 である場合には、燃焼理論に現れるより一般的なゼルドビッチ方程式が得られる[5]。そしてその特別な退化的な例は R(u) = u2 − u3 の場合に得られ、その方程式もまたゼルドビッチ方程式と呼ばれる[6]。
一成分の系のダイナミクスは、ある特定の制限に関するものである。なぜならば、その発展方程式は変分系
としても書かれ、したがってこれは次式で与えられる「自由エネルギー」 の永続的な減少を意味するからである。
ここで V(u) は R(u)=dV(u)/du であるようなポテンシャルを表す。

一つ以上の定常同次解を備える系において、典型的な解は、その同次状態をつなぐ進行波として与えられる。そのような解は、その形状を変えずに一定の速度で移動し、u(x, t) = û(ξ) と記述される。ここで ξ = x − ct であり c はその進行波の速度を表す。ここで、進行波は一般的に安定な構造を備えるが、非単調な定常解(例えば、前進と反前進のペアで構成される局所化された領域)は不安定であることに注意することである。c = 0 の場合には、この記述内容には次のような簡単な証明が存在する[7]:u0(x) が定常解、u=u0(x) + ũ(x, t) が無限小摂動解であるなら、線型安定性解析によって次の方程式が導かれる。
この解 ũ = ψ(x)exp(−λt) に対し、シュレディンガー型の固有値問題
が得られる。ただし、その負の固有値が解の不安定性に帰結するものである。平行移動不変性により、ψ = ∂xu0(x) は固有値 λ = 0 に対応する中立的な固有関数であり、その他のすべての固有関数は、ゼロ解の数について単調に増加する実固有値の絶対値について、増加する結び目の数に従って分類される。固有関数 ψ = ∂x u0(x) は少なくとも一つのゼロ解を持ち、非単調な定常解については対応する固有値 λ = 0 は最小のものではなく、したがって不安定性を意味する。
進行波の速度 c を決定するために、移動座標系を考え、定常解を探すことが出来る。
この方程式は、位置 û、時間 ξ、力 R、減衰係数 c に対する質量 D の動きに対する機械的な類似性を備えるものである。
空間一次元からより高次の空間次元に議論を移しても、依然として有効となる内容は数多く存在する。平らな、あるいは曲がった進行波は典型的な構造で、曲がった波の局所速度が局所曲率半径に依存するに従い、新たな効果が生じるものである(このことは極座標系を考えることで分かる)。この現象は、いわゆる曲率駆動不安定性を導く[8]。
二成分の反応拡散方程式[編集]
二成分の系は、一成分の系と比較してより幅広い現象を許すものである。アラン・チューリングによって初めて提唱されたある重要なアイデアに、局所的な系においては安定であっても拡散の存在する状況では不安定となる状態というものがある[9]。拡散は一般的には安定化効果と関連するものであるので、一聴するとこのアイデアは直感に反するもののようでもある。
しかしながら、線型化安定性解析によって、一般的な二成分系
を線型化するとき、定常同次解の平面波摂動
は次を満たすことが分かる。
チューリングのアイデアは、反応函数のヤコビアン R' の符号によって特徴付けられた系の四つの同値類においてのみ、理解されるものである。特に、有限の波ベクトル k が最も不安定なものであると仮定されたとき、そのヤコビアンは符号
を備えるものでなければならない。この系の類は、その第一の描写にちなみ活性因子・抑制因子系(activator-inhibitor system)と呼ばれる。すなわち、基底状態の近くではある成分は両成分の生産を促進するが、一方で別の成分はそれらの成長を阻害している。その最も傑出した代表例は、フィッツフュー=南雲方程式
である。ここで ƒ(u) = λu − u3 − κ は活動電位がどのように神経を移動するかを表している [10][11]。また du、dv、τ、σ および λ は正定数である。
活性因子・抑制因子系にパラメータの変化が施されたとき、均質な基底状態が安定であるような条件から、それが線型不安定であるような条件へと移ることがある。その対応する分岐は、支配的な波数 k = 0 を備える大域的な振動均質状態へのホップ分岐であるか、支配的な有限の波数を備える大域的なパターン状態へのチューリング分岐のいずれかであり得る。空間二次元における後者の分岐は、通常、ストライプや六角形のパターンを導くものである。
- 亜臨界チューリング分岐:フィッツフュー=南雲型の二成分反応拡散系におけるノイズの多い初期状態からの六角形パターンの形成。
-
t = 0のノイズの多い初期状態。
-
t = 10の系状態。
-
t = 100のほとんど収束した状態。
フィッツフュー=南雲の例に対し、そのチューリング分岐およびホップ分岐のための線型安定領域の境界を作る中立安定曲線は、次式で与えられる。
分岐が亜臨界であるなら、基底状態とパターンが共存するようなヒステリシスな領域において、しばしば局所的な構造(散逸ソリトン)が観測される。その他、頻繁に現れる構造としては、パルス列(周期進行波としても知られる)、螺旋波、ターゲットパターンがある。それら三つの解のタイプは、局所的なダイナミクスが安定なリミットサイクルを備えるような二成分(あるいはより多くの成分)の反応拡散方程式の、一般的な構造である[12]。
- フィッツフュー=南雲型の二成分の拡散反応系に現れる他のパターン。
-
回転する螺旋。
-
ターゲットパターン。
-
定常的な局所化されたパルス(散逸ソリトン)。
三成分およびそれ以上の成分の反応拡散方程式[編集]
様々な系に対して、二つよりも多い成分の反応拡散方程式が提唱されている。例えば、ベロウソフ・ジャボチンスキー反応のモデル[13]、血液凝固のモデル[14]あるいは平面の気体放電系[15]などが挙げられる。
より多くの成分を含む系では、一成分あるいは二成分の系では起こり得ないさまざまな現象(例えば、大域的フィードバックのない空間多次元における安定ランニングパルスなど)が起こることが知られている[16]。扱う系の性質に依存して起こり得る現象についての導入と系統的な概要については、[17]で与えられている。
応用と普遍性[編集]
近年、反応拡散系はパターン形成に対する基本的なモデルとして、多くの関心を集めている。上述のパターン(進行波、スパイラル、ターゲット、六角形、ストライプ、散逸ソリトン)は様々なタイプの反応拡散系において見られる。しかしそこには多くの矛盾、例えば、局所反応項においてそれらが見られるなど、が存在する。反応拡散過程は、生物学における形態形成と関連する過程に対する本質的な基盤であることも、述べられている[18] 。そして、それは動物の毛皮や、皮膚の色素沈着に対しても関連付けられている[19][20]。
反応拡散方程式のさらなる応用例は、生態の侵入[21]や感染症の拡がり[22]、腫瘍の成長[23][24][25]や、傷の治癒[26]などに見られる。反応拡散系が関心を集める別の理由には、それらが非線型偏微分方程式であるにもかかわらず、解析的な扱いがたびたび可能となることが挙げられる[7][8][27][28][29]。
実験[編集]
化学における反応拡散系のよく管理された実験には、現在三つの方法があることが知られている。第一に、ゲル型リアクター[30]あるいはキャピラリーチューブ[31]が用いられること。第二に、キャタリティック表面上の温度パルスが調べられること[32][33]。第三に、反応拡散系を用いて神経パルスの進行がモデル化されること[10][34]、である。
それらの一般的な例とは別に、適切な環境下ではプラズマ[35]や半導体[36]のような電気輸送系も、反応拡散の手法によって表現することが出来ることが判明している。それらの系に対して、パターン形成に関する様々な実験が行われている。
関連項目[編集]
参考文献[編集]
- ^ A. Kolmogorov et al., Moscow Univ. Bull. Math. A 1 (1937): 1
- ^ R. A. Fisher, Ann. Eug. 7 (1937): 355
- ^ A. C. Newell and J. A. Whitehead, J. Fluid Mech. 38 (1969): 279
- ^ L. A. Segel, J. Fluid Mech. 38 (1969): 203
- ^ Y. B. Zeldovich and D. A. Frank-Kamenetsky, Acta Physicochim. 9 (1938): 341
- ^ B. H. Gilding and R. Kersner, Travelling Waves in Nonlinear Diffusion Convection Reaction, Birkhäuser (2004)
- ^ a b P. C. Fife, Mathematical Aspects of Reacting and Diffusing Systems, Springer (1979)
- ^ a b A. S. Mikhailov, Foundations of Synergetics I. Distributed Active Systems, Springer (1990)
- ^ A. M. Turing, Phil. Transact. Royal Soc. B 237 (1952): 37
- ^ a b R. FitzHugh, Biophys. J. 1 (1961): 445
- ^ J. Nagumo et al., Proc. Inst. Radio Engin. Electr. 50 (1962): 2061
- ^ N. Kopell and L.N. Howard, Stud. Appl. Math. 52 (1973): 291
- ^ V. K. Vanag and I. R. Epstein, Phys. Rev. Lett. 92 (2004): 128301
- ^ E. S. Lobanova and F. I. Ataullakhanov, Phys. Rev. Lett. 93 (2004): 098303
- ^ H.-G. Purwins et al. in: Dissipative Solitons, Lectures Notes in Physics, Ed. N. Akhmediev and A. Ankiewicz, Springer (2005)
- ^ C. P. Schenk et al., Phys. Rev. Lett. 78 (1997): 3781
- ^ A. W. Liehr: Dissipative Solitons in Reaction Diffusion Systems. Mechanism, Dynamics, Interaction. Volume 70 of Springer Series in Synergetics, Springer, Berlin Heidelberg 2013, ISBN 978-3-642-31250-2.
- ^ L.G. Harrison, Kinetic Theory of Living Pattern, Cambridge University Press (1993)
- ^ H. Meinhardt, Models of Biological Pattern Formation, Academic Press (1982)
- ^ J. D. Murray, Mathematical Biology, Springer (1993)
- ^ E.E. Holmes et al, Ecology 75 (1994): 17
- ^ J.D. Murray et al, Proc. R. Soc. Lond. B 229 (1986: 111
- ^ M.A.J. Chaplain J. Bio. Systems 3 (1995): 929
- ^ J.A. Sherratt and M.A. Nowak, Proc. R. Soc. Lond. B 248 (1992): 261
- ^ R.A. Gatenby and E.T. Gawlinski, Cancer Res. 56 (1996): 5745
- ^ J.A. Sherratt and J.D. Murray, Proc. R. Soc. Lond. B 241 (1990): 29
- ^ P. Grindrod,Patterns and Waves: The Theory and Applications of Reaction-Diffusion Equations, Clarendon Press (1991)
- ^ J. Smoller, Shock Waves and Reaction Diffusion Equations, Springer (1994)
- ^ B. S. Kerner and V. V. Osipov, Autosolitons. A New Approach to Problems of Self-Organization and Turbulence, Kluwer Academic Publishers (1994)
- ^ K.-J. Lee et al., Nature 369 (1994): 215
- ^ C. T. Hamik and O. Steinbock, New J. Phys. 5 (2003): 58
- ^ H. H. Rotermund et al., Phys. Rev. Lett. 66 (1991): 3083
- ^ M. D. Graham et al., J. Phys. Chem. 97 (1993): 7564
- ^ A. L. Hodgkin and A. F. Huxley, J. Physiol. 117 (1952): 500
- ^ M. Bode and H.-G. Purwins, Physica D 86 (1995): 53
- ^ E. Schöll, Nonlinear Spatio-Temporal Dynamics and Chaos in Semiconductors, Cambridge University Press (2001)
外部リンク[編集]
- Java applet 反応拡散のシミュレーション
- Another applet グレイ=スコットの反応拡散
- Java applet いくつかの種の蛇に見られるパターン形成をシミュレートするための反応拡散
- Gallery 反応拡散の画像と動画
- TexRD software 反応拡散を基盤とするランダム・テクスチャー・ジェネレーター
- Reaction-Diffusion by the Gray-Scott Model: Pearson's parameterization グレイ=スコット反応拡散のパラメータ空間の可視図
- A Thesis 反応拡散パターンと分野の概観についての論文
- ReDiLab - Reaction Diffusion Laboratory ベロウソフ=ジャボチンスキー、グレイ=スコット、ウィラモフスキー=レスラーおよびフィッツフュー=南雲モデルをシミュレートした Flash & GPU based application(完全なソースコード付き)






![{\displaystyle {\mathfrak {L}}=\int \limits _{-\infty }^{\infty }\left[{\frac {D}{2}}(\partial _{x}u)^{2}-V(u)\right]{\text{d}}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c90197c12d2ff8dee1afc274f08e0c5d632b7b3f)











![{\displaystyle {\begin{aligned}q_{\text{n}}^{H}(k):&{}\quad {\frac {1}{\tau }}+(d_{u}^{2}+{\frac {1}{\tau }}d_{v}^{2})k^{2}&=f^{\prime }(u_{h}),\\[6pt]q_{\text{n}}^{T}(k):&{}\quad {\frac {\kappa }{1+d_{v}^{2}k^{2}}}+d_{u}^{2}k^{2}&=f^{\prime }(u_{h}).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fa5f0d7344114fdbd83fdb79ce83296ae151a75)