パルス幅変調

パルス幅変調（パルスはばへんちょう、英語: pulse width modulation、PWM）とは変調方法の一つであり、パルス波のデューティ比を変化させて変調すること。

• 機械工学などにおいては、スイッチオン／オフの比率を変化させる手法。
• シンセサイザーで、パルス波のデューティ比を変化させること。

パルス幅変調の式

パルス幅変調の数学的扱いは次のようになる。簡単のため、入力信号として正弦波 $\;v(t)=v\sin \omega t\;$ の場合を考える。 ここで $\;v\;$ は次元を持ったある定数、$\;\omega \;$、$\;t\;$ はそれぞれ角振動数、時間である。 また、変調されていないときのパルス波は、周期 $\;T\;$ ごとに幅 $\;\tau \;$ （ただし$\;0<\tau <T\;$）の パルスを出力するものと仮定する。 このとき、パルス幅変調された信号 $\;S(t)\;$ は、周期 $\;T\;$ ごとに幅 $\;\Delta T=\tau (1+m\sin \omega t)\;$ のパルスが出力されるように変調される。 $\;m\;$ は変調度で、$\;0<\Delta T<T\;$ でなければならないので $\;0<m<{\frac {T}{\tau }}-1\;$ を満足しなければならない。

$\;S(t)=W\sum _{n=-\infty }^{\infty }\left(\Theta \left(t-nT\right)-\Theta \left(t-\left(nT+\Delta T\right)\right)\right),\;$

ここで、$\;\Theta (x)\;$はヘヴィサイドの階段関数、 $\;W\;$は次元を持ったなんらかの定数である。 ヘヴィサイドの階段関数のフーリエ変換表示

$\;\Theta (x)=\lim _{\epsilon \to +0}\int _{-\infty }^{\infty }{\frac {dp}{2\pi i}}{\frac {1}{p-i\epsilon }}e^{ipx},\quad i:={\sqrt {-1\,}},\;$

や公式

$\;{\frac {1}{2\pi }}\sum _{n=-\infty }^{\infty }e^{2\pi inx}=\sum _{l=-\infty }^{\infty }\delta (x-2\pi l),\qquad x\in \mathbb {R} ,\;$

を用い(ただし、$\;\delta (x)\;$はディラックのデルタ関数) 、 適時積分と和の入れ替えを行うと、 $\;S(t)\;$は

$\;S(t)=S_{0}(t)+S'(t),\;$

$\;{\begin{aligned}S_{0}(t)&=\lim _{l,\epsilon \rightarrow +0}{\frac {W}{2\pi il+\epsilon }}\left(e^{2\pi ilt/T}-e^{2\pi il(t-\Delta T)/T}\right)=W{\frac {\Delta T}{T}},\\S'(t)&=\sum _{l\neq 0}{\frac {W}{i}}{\frac {1}{2\pi l-i\epsilon }}e^{2\pi ilt/T}(1-e^{-2\pi il\Delta T/T})\end{aligned}}\;$

と書ける。 ここで、$\;S(t)\;$が時間の並進$\;t\longrightarrow t+\Delta T/2\;$に対して 不変であることを用いると、 $\;S'(t)\;$をもう少しきれいに書き直すことができて、

$S'(t)=\sum _{l=1}^{\infty }{\frac {2W}{\pi l}}\cos \left({\frac {2\pi l}{T}}t\right)\sin \left({\frac {\pi l}{T}}\Delta T\right)$

である。最後の項$\;\sin \left(\pi l/T\Delta T\right)\;$に$\;\Delta T=\tau (1+m\sin \omega t)\;$を代入すると、 これはFM変調の式であることがわかる。

$\;S_{0}(t)=W{\frac {\tau }{T}}(1+m\sin \omega t)\;$であるから、 ローパスフィルタで$\;S'(t)\;$を除去できれば、$\;W{\frac {\tau }{T}}\;$分シフトされて 元の信号が復調される。

用途

アナログシンセサイザー

エンベロープジェネレーターやLFOなどサブオシレータでパルス幅を変化させ、

• 発振するほどの高速変化により、独特の非整数倍音を生成すること。
• 音量エンベロープのような低速変化により、連続的に音色変化（パルス波から矩形波など）させること。

音源チップ

• ゲームボーイアドバンスで使用されている。
• P/ECEで使用されている。
• スーパー32Xで使用されている。
• ファミリーコンピュータ ディスクシステム音源が波形メモリからの出力に採用しているとの説あり。
  • ファミコンディスクシステム音源は波形メモリに周波数変調をかけることができ、出力はPWM、という説あり。
• ワンダースワン音源が波形メモリからの出力に採用しているとの説あり。

電源回路

インバータにより直流を交流に変換したり、チョッパ制御により直流電圧を制御する他、整流器（PWMコンバータともいう）としても用いられる。いずれも電源電圧より高い電圧を得るためにはリアクトルの充放電機能を用いる。また脈流や高調波となって出力されるため、やはりリアクトルを用いてそれらを平滑化する必要がある。

チョッパ制御

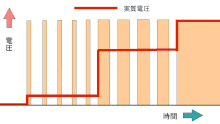チョッパ制御におけるPWMの例

詳細は「チョッパ制御」を参照

高周波分巻式を除くチョッパ制御の場合、パルスの周波数は一定であり、パルスの幅だけを変化させることで平均電圧を可変とする。パルス幅が狭い場合は平均電圧が下がり、パルス幅が広いときは平均電圧が上がる。例えば次のパルスまでを10等分したとして、ON:OFFを2:8とすれば元の電圧の2/10つまり1/5になり、8:2なら8/10=4/5の電圧が得られる。100%の電圧が必要なときは単にONのままにするが、チョッパ装置そのものも抵抗となるため、それを短絡して直接負荷に流すこともある。

インバータ

インバータにおけるPWMの例

詳細は「インバータ」を参照

PWMで制御するインバータの場合はマイコンにより、スイッチング素子のゲート電極に信号を流すタイミングを決めるために、一般的な方法として搬送波ベースのものがあり、これは搬送波(もしくはキャリア)と呼ばれる三角波と、基本波(もしくは信号波)と呼ばれる正弦波からタイミングを生成するものである。ゲート電極に信号を流すゲートドライブが搬送波と基本波の交点を検出し、4個（単相交流）または6個（三相交流）のスイッチング素子をオン／オフする。すると右図のようなパルス（黄色い矩形）が得られ、その平均電圧（赤い線）が疑似正弦波交流になるのである。これ以外にもタイミングを決める方法はあるがここでは割愛する。

2レベル、3レベルというのは、パルスの電圧の程度である。3レベルインバータの出力電圧は100%、0%に加え、50%の電圧も得られる。2レベルでは0%と100%だけとなる。商用電源も発電所や変電所など、3、5、9レベルというような複雑な回路のインバータで、発電された電力変動の平滑化などを行なう。このようなインバータをマルチレベルインバータと称する。レベルが高ければ高いほど（数が大きいほど）得られる電圧の種類が増え、擬似正弦波が滑らかな曲線に近づいていく。反面、インバータの回路は複雑になっていく。

参考文献

• F.R.コナー 著、高原幹夫 訳『変調入門』森北出版〈電子通信工学シリーズ5〉、1985年。ISBN 4-627-73350-X。