atan2

atan2（アークタンジェント2）は、関数の一種。「2つの引数を取るarctan（アークタンジェント）」という意味である。x軸の正の向きと、点 $(x, y)$ （ただし、 $(0, 0)$ ではない）まで伸ばした半直線（レイ）との間の、ユークリッド平面上における角度として定義される。関数は $\operatorname {atan2} (y,x)$ もしくは $\operatorname {arctan2} (y,x)$ の形をとり、値はラジアンで返ってくる。

関数 $\operatorname {atan2} (y,x)$ は、プログラミング言語のFortran (IBM社が1961年に実装したFORTRAN-IV)において最初に登場した。元々は、角度 $θ$ を直交座標系の $(x, y)$ から極座標系の $(r, θ)$ に変換する際に、正確で一意な値が返ってくることを意図して導入された。また、 $\operatorname {atan2} (y,x)$ は複素数 $x+iy$ の偏角 (「位相」とも言う)を求める際にも利用される。

関数 $\operatorname {atan2} (y,x)$ は、 $- π < θ \leq π$ の範囲で、

{\begin{aligned}x&=r\cos \theta \\y&=r\sin \theta \end{aligned}}

（ただし、 $r > 0$ ）となる単一の値 $θ$ を返す。

なお、arctanを使って角度 $θ$ を求める際に注意すべきことであるが、 $r={\sqrt {x^{2}+y^{2}}}$ が真であるからと言って、

\theta =\arctan \left({\frac {y}{x}}\right)

であるということが常に言えるとは限らない。

これは、 $x > 0$ だった場合にのみ当てはまる。もし $x < 0$ だった場合は、上の式から導出された角度は、正しい角度とは正反対の方向を指し示している。そして、デカルト点 $(x, y)$ をユークリッド平面上の正しい象限に配置するには、Π（度数法で言うと180°）の値を $θ$ に加算または減算する必要がある^[1]。これはつまり、正しい角度を出すためには $x$ および $y$ の符号の情報がそれぞれ別個に必要とされると言うことであり、もし単に $y$ を $x$ で除算した場合は、その情報が失われてしまうというわけである。その点、atan2は細かいことを気にしなくてもyとxに代入すれば普通に正しい角度を返してくれるので便利である。

関数 $\operatorname {atan2} (y,x)$ の戻り値である角度 $θ$ については、 $x$ と $y$ の値を変更しないままでも角度 $θ$ に $2 π$ の任意の整数倍を加算することが可能であるため、つまり区間をちゃんと設定しないと戻り値の値が曖昧になってしまうため、関数atan2はその主値として、区間を $(- π, π]$ としたものが戻り値として返ってくるようになっている（関数arctanの戻り値の区間が(− $π$ /2 , $π$ /2)である点との違いに注意）。角度 $θ$ は符号付き角度であり、反時計回りの角度は正、時計回りは負となる。具体的に言うと、もし $y \geq 0$ だった場合は $[0, π]$ の区間にあり、もし $y < 0$ だった場合には $(- π, 0)$ の区間にある、と言う感じになるように関数 $\operatorname {atan2} (y,x)$ の内部で場合分けをしている。

atan2が生み出された経緯と動機

$atan2$ 関数は、元々は特定のプログラミング言語に実装された関数の一つに過ぎなかったが、現在では他の科学技術の分野でもよく使われるものとなっている。その起源は少なくとも、古のプログラミング言語であるFORTRANにまで遡ることができるが^[2]、現在においては他の現代的なプログラミング言語においても実装されている。例を挙げると、C言語のmath.h 標準Cライブラリ、JavaのMathライブラリ、.NETのSystem.Math (C#やVB.NETなどから利用できる)、Pythonのmathモジュール、RubyのMathモジュール、Goのmathパッケージ^[3]、などであるが、もちろん他にもたくさんの言語に実装されている。さらに言うと、Perlを始めとするスクリプト言語にも、C言語風のatan2(y, x)関数が実装されていることが多い。

atan2関数が生み出された背景として、単一引数のみを取るアークタンジェント（arctan関数）は正反対の方向を区別できない、と言う使い勝手の悪さがある。例えば、 $x$ 軸とベクトル $(1, 1)$ がなす反時計回りの角度を、arctan関数を使って「 $arctan(1/1)$ 」のような形で計算した場合、「 $π/4$ ラジアン（つまり度数法で言うと $45°$ ）」という答えが返ってくる。しかし、 $x$ 軸とベクトル $(-1, -1)$ の間の角度を同様に、「 $arctan(-1/-1)$ 」のような形で計算してみると、期待される答えは「 $-3π/4$ ラジアン(−135°)」または「 $5π/4$ ラジアン(225°)」であるにもかかわらず、やっぱり「 $π/4$ ラジアン」が返ってくる。arctan関数の使い勝手の悪さをさらに言うと、 $x$ 軸とベクトル $(0, y)(ただし、 y \neq 0とする)$ がなす角度をarctan関数で計算しようとすると、これは $arctan(y /0)$ の評価が必要になるわけだが、こんなことをさせるとコンピューターはゼロ除算のエラーを吐いてバグる。

atan2関数は、2つの変数 $y$ と $x$ から一意なアークタンジェントの値を算出するが、そのとき両変数の正負の符号が、実行結果の象限を決定するために利用される。それに基づいて、アークタンジェントで「 $y / x$ 」したときの結果の中から、求める値が出るような分岐先に飛ばしている。例を挙げると、「 $atan2(1, 1) = π/4$ 」と「 $atan2(-1, -1) = -3π/4$ 」のどちらに分岐するのか、と言ったことを判別している。また、例えば「ゼロ除算のエラーを吐いてバグる」の代わりに「 $atan2(1, 0) = π/2$ 」に分岐させるときも、同様の方法で飛ばしている。

もちろん、場合によって必要な象限補正と例外処理をいちいち精査することで、上記の計算を力技で行うことは可能だが、そんなことをするよりも、常に一意な正しい結果を提供するような1つの関数を使った方が便利である。そんな経緯でatan2関数が存在する。 $atan2$ 関数は様々な応用（アプリケーション）において有用であり、例えばユークリッド空間上におけるユークリッド点に関して、1つの点から別の点へと至る方向ベクトルを調べるのに便利である。主な用途としては、コンピューターグラフィックス（CG）における回転において、回転行列をオイラー角に変換する際に使われる。

定義と計算

定義

関数 $atan2$ は複素数 $x + y i$ に偏角関数 $arg$ を適用した時の主値を計算する。すなわち、 $atan2(y, x) = Pr arg(x + y i) = Arg(x + y i)$ である。偏角は、 $2π$ （原点を中心としたちょうど1周の回転に対応）の整数倍を加えたものも同じ角度になるが、 $atan2$ を一意に定義するために範囲 $(-\pi ,\pi ]$ の主値を使用する。つまり、 $- π < atan2(y, x) \leq π$ とする。

標準の $arctan$ 関数（値域 $(-π/2, π/2)$ ）を用いて、次のように表すことができる:

\operatorname {atan2} (y,x)={\begin{cases}\arctan({\frac {y}{x}})&{\text{if }}x>0,\\\arctan({\frac {y}{x}})+\pi &{\text{if }}x<0{\text{ and }}y\geq 0,\\\arctan({\frac {y}{x}})-\pi &{\text{if }}x<0{\text{ and }}y<0,\\+{\frac {\pi }{2}}&{\text{if }}x=0{\text{ and }}y>0,\\-{\frac {\pi }{2}}&{\text{if }}x=0{\text{ and }}y<0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}

重複する4つの半平面を用いたコンパクトな式:

\operatorname {atan2} (y,x)={\begin{cases}\arctan \left({\frac {y}{x}}\right)&{\text{if }}x>0,\\{\frac {\pi }{2}}-\arctan \left({\frac {x}{y}}\right)&{\text{if }}y>0,\\-{\frac {\pi }{2}}-\arctan \left({\frac {x}{y}}\right)&{\text{if }}y<0,\\\arctan \left({\frac {y}{x}}\right)\pm \pi &{\text{if }}x<0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}

アイバーソンの記法を用いれば、さらにコンパクトな式が可能:

$\operatorname {atan2} (y,x)$	$=\arctan \left({\frac {y}{x}}\right)[x\neq 0]+\operatorname {sgn}(y)\left(\pi [x<0]+{\frac {\pi }{2}}[x=0]\right)$
	$+\;{\text{undefined}}\;\![x=0\wedge y=0]$ ^{[note 1]}

一見すると条件式のない数式:

\operatorname {atan2} (y,x)=\operatorname {sgn}(x)^{2}\arctan \left({\frac {y}{x}}\right)+{\frac {1-\operatorname {sgn}(x)}{2}}\left(1+\operatorname {sgn}(y)-\operatorname {sgn}(y)^{2}\right)\pi

タンジェントの半角の公式から派生した次の式で $atan2$ を定義することもできる:

\operatorname {atan2} (y,x)={\begin{cases}2\arctan \left({\frac {y}{{\sqrt {x^{2}+y^{2}}}+x}}\right)&{\text{if }}x>0{\text{ or }}y\neq 0,\\\pi &{\text{if }}x<0{\text{ and }}y=0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}

この式は、上記の定義よりもシンボリックな使用に適している場合がある。ただし、 ${\sqrt {x^{2}+y^{2}}}$ の丸め誤差の影響が領域 $x < 0, y = 0$ の近くで拡大するため、一般的な浮動小数点数の計算用途には適していない（これにより、yがゼロで除算されることもある）。

これらの膨らんだ丸め誤差を回避するため、先ほどの式を変形:

\operatorname {atan2} (y,x)={\begin{cases}2\arctan \left({\frac {y}{{\sqrt {x^{2}+y^{2}}}+x}}\right)&{\text{if }}x>0,\\2\arctan \left({\frac {{\sqrt {x^{2}+y^{2}}}-x}{y}}\right)&{\text{if }}x\leq 0{\text{ and }}y\neq 0,\\\pi &{\text{if }}x<0{\text{ and }}y=0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}

注意:

これにより、範囲 $(-π, π]$ の結果が生成される。^{[note 2]}
上記のように、偏角の主値 $atan2(y, x)$ は、三角法によって $arctan(y / x)$ に関連付けることができる。導出は次のようになる:

(x, y) = (r cos θ, r sin θ)

のとき

tan(θ /2) = y / (r + x)

となる。その結果、次式が成立する。

{\text{atan2}}(y,x)=\theta =2\,\theta /2=2\arctan {\frac {y}{{\sqrt {x^{2}+y^{2}}}+x}}.

問題の領域は

\sqrt x 2 + y 2 + x \neq 0

であることに注意。

微分

詳細は「回転数 (数学)」を参照

関数 $atan2$ は2変数関数であるため、2つの偏導関数がある。これらの導関数が存在する点では、 $atan2$ は定数項を除いた $arctan(y / x)$ に等しくなる。したがって、 $x > 0$ または $y \neq 0$ の場合、

{\begin{aligned}&{\frac {\partial }{\partial x}}\operatorname {atan2} (y,\,x)={\frac {\partial }{\partial x}}\arctan \left({\frac {y}{x}}\right)=-{\frac {y}{x^{2}+y^{2}}},\\[5pt]&{\frac {\partial }{\partial y}}\operatorname {atan2} (y,\,x)={\frac {\partial }{\partial y}}\arctan \left({\frac {y}{x}}\right)={\frac {x}{x^{2}+y^{2}}}.\end{aligned}}

したがって、atan2 の勾配は次式で与えられる。

\nabla {\text{atan2}}(y,x)=\left({-y \over x^{2}+y^{2}},\ {x \over x^{2}+y^{2}}\right).

関数 $atan2$ を角度関数 $θ (x, y) = atan2(y, x)$ （定数を除いて定義）として省略して表すと、全微分について次の式が得られる:

{\begin{aligned}\mathrm {d} \theta &={\frac {\partial }{\partial x}}\operatorname {atan2} (y,\,x)\,\mathrm {d} x+{\frac {\partial }{\partial y}}\operatorname {atan2} (y,\,x)\,\mathrm {d} y\\[5pt]&=-{\frac {y}{x^{2}+y^{2}}}\,\mathrm {d} x+{\frac {x}{x^{2}+y^{2}}}\,\mathrm {d} y.\end{aligned}}

関数 $atan2$ は、負の $x$ 軸に沿って不連続であるが、角度を連続的に定義できないという事実を反映して、この導関数は原点を除いて連続的に定義される。これは、角度の微小な（そして実際には局所的な）変化が原点を除くすべての場所で定義できるという事実を反映している。この導関数をパスに沿って積分するとパス全体の角度が全体的に変化し、閉ループで積分すると回転数が得られる。

微分幾何学の言語では、この導関数は1-形式であり、閉である（導関数が0である）が、完全ではない（0-形式の導関数、つまり関数ではない）。実際、1点を除いた平面（Punctured Plane）の1次のド・ラームコホモロジーを生成する。これはそのような形式の最も基本的な例であり、微分幾何学の基本である。

$atan2$ の偏導関数には三角関数が含まれていないため、三角関数の評価にコストがかかる可能性がある多くのアプリケーション（例：組み込みシステム）で特に役立つ。

Illustrations

This figure shows values of atan2 along selected rays from the origin, labelled at the unit circle. The values, in radians, are shown inside the circle. The diagram uses the standard mathematical convention that angles increase counterclockwise from zero along the ray to the right. Note that the order of arguments is reversed; the function $atan2(y, x)$ computes the angle corresponding to the point $(x, y)$ .

Comparison of arctan and atan2 functions

This figure shows the values of $\arctan(\tan(\theta ))$ along with $\operatorname {atan2} (\sin(\theta ),\cos(\theta ))$ for $0\leq \theta \leq 2\pi$ . Both functions are odd and periodic with periods $\pi$ and $2\pi$ , respectively, and thus can easily be supplemented to any region of real values of $\theta$ . One can clearly see the branch cuts of the $\operatorname {atan2}$ -function at $\theta =\pi$ , and of the $\arctan$ -function at $\theta \in \{{\tfrac {\pi }{2}},\;{\tfrac {3\pi }{2}}\}$ .^[4]

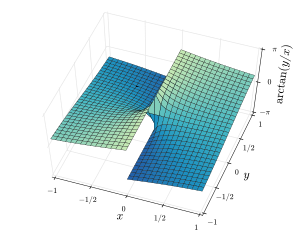
The two figures below show 3D views of respectively $atan2(y, x)$ and $arctan(y / x)$ over a region of the plane. Note that for $atan2(y, x)$ , rays in the X/Y-plane emanating from the origin have constant values, but for $arctan(y / x)$ lines in the X/Y-plane passing through the origin have constant values. For $x > 0$ , the two diagrams give identical values.

Angle sum and difference identity

詳細は「三角関数の公式の一覧#加法定理」を参照

Sums of $\operatorname {atan2}$ may be collapsed into a single operation according to the following identity

\operatorname {atan2} (y_{1},x_{1})\pm \operatorname {atan2} (y_{2},x_{2})=\operatorname {atan2} (y_{1}x_{2}\pm y_{2}x_{1},x_{1}x_{2}\mp y_{1}y_{2})

...provided that $\operatorname {atan2} (y_{1},x_{1})\pm \operatorname {atan2} (y_{2},x_{2})\in (-\pi ,\pi ]$ .

The proof involves considering two cases, one where $y_{2}\neq 0$ or $x_{2}>0$ and one where $y_{2}=0$ and $x_{2}<0$ .

We only consider the case where $y_{2}\neq 0$ or $x_{2}>0$ . To start, we make the following observations:

$-\operatorname {atan2} (y,x)=\operatorname {atan2} (-y,x)$ provided that $y\neq 0$ or $x>0$ .
$\operatorname {Arg} (x+iy)=\operatorname {atan2} (y,x)$ , where $\operatorname {Arg}$ is the complex argument function.
$\theta =\operatorname {Arg} e^{i\theta }$ whenever $\theta \in (-\pi ,\pi ]$ , a consequence of Euler's formula.
$\operatorname {Arg} (e^{i\operatorname {Arg} \zeta _{1}}e^{i\operatorname {Arg} \zeta _{2}})=\operatorname {Arg} (\zeta _{1}\zeta _{2})$ .

To see (4), we have the identity $e^{i\operatorname {Arg} \zeta }={\bar {\zeta }}$ where ${\bar {\zeta }}=\zeta /\left|\zeta \right|$ , hence $\operatorname {Arg} (e^{i\operatorname {Arg} \zeta _{1}}e^{i\operatorname {Arg} \zeta _{2}})=\operatorname {Arg} ({\bar {\zeta _{1}}}{\bar {\zeta _{2}}})$ . Furthermore, since $\operatorname {Arg} \zeta =\operatorname {Arg} a\zeta$ for any positive real value $a$ , then if we let $\zeta =\zeta _{1}\zeta _{2}$ and $a={\frac {1}{\left|\zeta _{1}\right|\left|\zeta _{2}\right|}}$ then we have $\operatorname {Arg} ({\bar {\zeta _{1}}}{\bar {\zeta _{2}}})=\operatorname {Arg} (\zeta _{1}\zeta _{2})$ .

From these observations have following equivalences:

{\begin{aligned}\operatorname {atan2} (y_{1},x_{1})\pm \operatorname {atan2} (y_{2},x_{2})&{}=\operatorname {atan2} (y_{1},x_{1})+\operatorname {atan2} (\pm y_{2},x_{2})&{\text{by (1)}}\\&{}=\operatorname {Arg} (x_{1}+iy_{1})+\operatorname {Arg} (x_{2}\pm iy_{2})&{\text{by (2)}}\\&{}=\operatorname {Arg} e^{i(\operatorname {Arg} (x_{1}+iy_{1})+\operatorname {Arg} (x_{2}\pm iy_{2}))}&{\text{by (3)}}\\&{}=\operatorname {Arg} (e^{i\operatorname {Arg} (x_{1}+iy_{1})}e^{i\operatorname {Arg} (x_{2}\pm iy_{2})})\\&{}=\operatorname {Arg} ((x_{1}+iy_{1})(x_{2}\pm iy_{2}))&{\text{by (4)}}\\&{}=\operatorname {Arg} (x_{1}x_{2}\mp y_{1}y_{2}+i(y_{1}x_{2}\pm y_{2}x_{1}))\\&{}=\operatorname {atan2} (y_{1}x_{2}\pm y_{2}x_{1},x_{1}x_{2}\mp y_{1}y_{2})&{\text{by (2)}}\end{aligned}}

Corollary: if $(y_{1},x_{1})$ and $(y_{2},x_{2})$ are 2-dimensional vectors, the difference formula is frequently used in practice to compute the angle between those vectors with the help of $\operatorname {atan2}$ , since the resulting computation behaves benign in the range $(-\pi ,\pi ]$ and can thus be used without range checks in many practical situations.

Realizations of the function in common computer languages

The realization of the function differs from one computer language to another:

The C function atan2, and most other computer implementations, are designed to reduce the effort of transforming cartesian to polar coordinates and so always define atan2(0, 0). On implementations without signed zero, or when given positive zero arguments, it is normally defined as 0. It will always return a value in the range $[-π, π]$ rather than raising an error or returning a NaN (Not a Number).

In Common Lisp, where optional arguments exist, the atan function allows one to optionally supply the x coordinate: (atan y x).^[5]
In Mathematica, the form ArcTan[x, y] is used where the one parameter form supplies the normal arctangent (note that the order of arguments is reversed relative to the convention used in the discussion above). Mathematica classifies ArcTan[0, 0] as an indeterminate expression.
In Microsoft Excel,^[6] OpenOffice.org Calc, LibreOffice Calc,^[7] Google Spreadsheets,^[8] iWork Numbers,^[9] and ANSI SQL:2008 standard,^[10] the atan2 function has the two arguments reversed.
In the Intel Architecture assembler code, atan2 is known as the FPATAN (floating-point partial arctangent) instruction.^[11] It can deal with infinities and results lie in the closed interval $[-π, π]$ , e.g. atan2(∞, x) = + $π$ /2 for finite x. Particularly, FPATAN is defined when both arguments are zero:
atan2(+0, +0) = +0;

atan2(+0, −0) = + $π$ ;

atan2(−0, +0) = −0;

atan2(−0, −0) = − $π$ .

This definition is related to the concept of signed zero.

On most TI graphing calculators (excluding the TI-85 and TI-86), the equivalent function is called R►Pθ and has the arguments reversed.
On TI-85 the $arg$ function is called angle(x,y) and although it appears to take two arguments, it really only has one complex argument which is denoted by a pair of numbers: $x + y i = (x, y)$ .
In mathematical writings other than source code, such as in books and articles, the notations Arctan^[12] and Tan⁻¹^[13] have been utilized; these are capitalized variants of the regular arctan and tan⁻¹. This usage is consistent with the complex argument notation, such that $Atan(y, x) = Arg(x + y i)$ .
On HP calculators, treat the coordinates as a complex number and then take the ARG. Or << C->R ARG >> 'ATAN2' STO.
On scientific calculators the function can often be calculated as the angle given when $(x, y)$ is converted from rectangular coordinates to polar coordinates.
Systems supporting symbolic mathematics normally return an undefined value for $atan2(0, 0)$ or otherwise signal that an abnormal condition has arisen.
For systems implementing signed zero, infinities, or Not a Number (for example, IEEE floating point), it is common to implement reasonable extensions which may extend the range of values produced to include − $π$ and −0. These also may return NaN or raise an exception when given a NaN argument.
For systems implementing signed zero (for example, IEEE floating point), $atan2(-0, x)$ , $x$ < 0 poses the risk of returning the value − $π$ , in the case where the implementation of $atan2(y, x)$ fails to properly handle −0 inputs.
The free math library FDLIBM (Freely Distributable LIBM) available from netlib has source code showing how it implements atan2 including handling the various IEEE exceptional values.
For systems without a hardware multiplier the function $atan2$ can be implemented in a numerically reliable manner by the CORDIC method. Thus implementations of $atan(y)$ will probably choose to compute $atan2(y, 1)$ .

References

^ http://scipp.ucsc.edu/~haber/ph116A/arg_11.pdf
^ Organick, Elliott I. (1966). A FORTRAN IV Primer. Addison-Wesley. pp. 42. "Some processors also offer the library function called ATAN2, a function of two arguments (opposite and adjacent)."
^ “src/math/atan2.go”. The Go Programming Language. 2018年4月20日閲覧。
^ “Wolf Jung: Mandel, software for complex dynamics”. www.mndynamics.com. 2018年4月20日閲覧。
^ “CLHS: Function ASIN, ACOS, ATAN”. LispWorks. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
^ “Microsoft Excel Atan2 Method”. Microsoft. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
^ “LibreOffice Calc ATAN2”. Libreoffice.org. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
^ “Google Spreadsheets' Function List”. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
^ “Numbers' Trigonometric Function List”. Apple. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
^ “ANSI SQL:2008 standard”. Teradata. 2015年8月20日時点のオリジナルよりアーカイブ。 Template:Cite webの呼び出しエラー：引数 accessdate は必須です。
^ IA-32 Intel Architecture Software Developer’s Manual. Volume 2A: Instruction Set Reference, A-M, 2004.
^ Burger, Wilhelm; Burge, Mark J. (7 July 2010). Principles of Digital Image Processing: Fundamental Techniques. Springer Science & Business Media. ISBN 9781848001916 2018年4月20日閲覧。
^ Glisson, Tildon H. (18 February 2011). Introduction to Circuit Analysis and Design. Springer Science & Business Media. ISBN 9789048194438 2018年4月20日閲覧。

External links

ATAN2 Online calculator
Java 1.6 SE JavaDoc
atan2 at Everything2
PicBasic Pro solution atan2 for a PIC18F

Other implementations/code for atan2

Notes

^ Thereby
${\text{undefined}}\cdot 0=0,$

${\text{undefined}}\cdot 1={\text{undefined}}$ and

$z+{\text{undefined}}={\text{undefined}}$ for every $z.$
^ 結果の周期性を適用して、別の目的の範囲に写像できる。e.g. 負の結果に $2π$ を加算すると $[0, 2π)$ に写像できる。

[1] ttp://scipp.ucsc.edu/~haber/ph116A/arg_11.pdf

[2] Organick, Elliott I. (1966). A FORTRAN IV Primer. Addison-Wesley. pp. 42. "Some processors also offer the library function called ATAN2, a function of two arguments (opposite and adjacent)."

[3] “src/math/atan2.go”. The Go Programming Language. 2018年4月20日閲覧。

[6] “Wolf Jung: Mandel, software for complex dynamics”. www.mndynamics.com. 2018年4月20日閲覧。

[7] “CLHS: Function ASIN, ACOS, ATAN”. LispWorks. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。

[8] “Microsoft Excel Atan2 Method”. Microsoft. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。

[9] “LibreOffice Calc ATAN2”. Libreoffice.org. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。

[10] “Google Spreadsheets' Function List”. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。

[11] “Numbers' Trigonometric Function List”. Apple. Template:Cite webの呼び出しエラー：引数 accessdate は必須です。

[12] “ANSI SQL:2008 standard”. Teradata. 2015年8月20日時点のオリジナルよりアーカイブ。 Template:Cite webの呼び出しエラー：引数 accessdate は必須です。

[13] IA-32 Intel Architecture Software Developer’s Manual. Volume 2A: Instruction Set Reference, A-M, 2004.

[14] Burger, Wilhelm; Burge, Mark J. (7 July 2010). Principles of Digital Image Processing: Fundamental Techniques. Springer Science & Business Media. ISBN 9781848001916 2018年4月20日閲覧。

[15] Glisson, Tildon H. (18 February 2011). Introduction to Circuit Analysis and Design. Springer Science & Business Media. ISBN 9789048194438 2018年4月20日閲覧。

[4] Thereby
${\text{undefined}}\cdot 0=0,$

${\text{undefined}}\cdot 1={\text{undefined}}$ and

$z+{\text{undefined}}={\text{undefined}}$ for every $z.$

[5] 結果の周期性を適用して、別の目的の範囲に写像できる。e.g. 負の結果に $2π$ を加算すると $[0, 2π)$ に写像できる。

[1]

[2]

[3]

[note 1]

[note 2]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]