複比
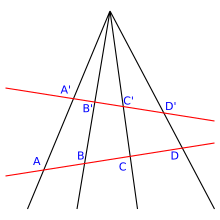
複比(ふくひ、英: double ratio)は、幾何学における概念の1つで、交差比(こうさひ、英: cross-ratio)および非調和比(ひちょうわひ、英: anharmonic ratio)とも呼ばれ、4つの共線上の点、特に射影直線上の点の集合に関連付けられた数値である。直線上の4つの点 A, B, C, D が与えられると、それらの複比は次のように定義される。
ここで、各距離の符号は線の向きによって決まり、距離はユークリッド空間に射影されて測定される。(4つの点の1つが直線の無限遠点である場合、その点を含む2つの距離は式から削除される。)複比が正確に-1の場合、点DはAとBに対するCの調和共役であり、調和比と呼ばれる。したがって、複比は、4つ組の調和比からの偏差を測定するものとみなせる。そのため非調和比とも呼ばれる。
複比は線形分数変換の下で不変である。これは本質的に4つの同一線上の点の唯一の射影不変量である。このことは射影幾何学の根底にある重要な性質である。
複比は、古代よりおそらくはユークリッドによって定義され、パップスによってその重要な普遍性特性に注目した考察がなされた。19世紀には広く研究されるようになった。[1]
射影平面上で1点で交わる4線(英: concurrent lines)や、リーマン球面上の4点についての派生した概念も存在する。双曲幾何学のケイリー・クラインモデルでは、特定の複比により点間の距離が表される。
用語と歴史[編集]

アレクサンドリアのパップスは、自身の著書Collection: Book VIIの中で複比に相当する概念を暗に使用した。パップスの初期の読者には、アイザック・ニュートン、ミシェル・シャール、ロバート・シムソンが含まれる。 1986年、アレクサンダー・ジョーンズはパップスの原文を翻訳し、パップスの補題が現代の用語とどのように関係しているかについて解説を書いた。[2]
射影幾何学における複比の現代的な使用は、1803 年にラザール・カルノーの著書Géométrie de Positionで始まった。使用された用語は、 le rapport anharmonique(非調和比)であった。ドイツの幾何学者はそれをdas Doppelverhältnis(複比)と呼んだ。
直線上の3点が与えられたとき、複比が-1になる4番目の点は射影調和共役と呼ばれる。 1847 年に、カール・フォン・シュタウトは4番目の点の構成をスロー(英: throw, 独: Wurf) と呼び、この構成を使用して、幾何学で暗黙的な算術演算を示した。彼によるスロー代数は、通常は公理とみなされるが、射影幾何学で証明された数値命題へのアプローチを提供している。[3]
英語の"cross-ratio"という用語は、1878 年にウィリアム・キングドン・クリフォードによって導入された。[4]
定義[編集]
座標z1, z2, z3, z4の実数直線上の4つの異なる点の複比は次の式で与えられる。
また、2つの3点の分割比率の「複比」として記述することもできる。
複比は通常、 z1, z2, z3, z4のいずれかが無限大の場合にも拡張される。これは、無限大となる点を含む2箇所を削除することにより行われる。例:
ユークリッド幾何学では、 A, B, C, D が共線上の点である場合、複比は次のように表される。
ここで、各距離の符号は、線の一貫した方向に従って決定される。
同じ式を4つの異なる複素数、またはより一般的には任意の体の元にも適用でき、1つが∞の場合は上記のような拡張が可能である。
性質[編集]
共線上の4点 A, B, C, D の複比は、次のように記述できる。
ここでは点Cが線分を分割する比率を表し、 は点Dが同じ線分を分割する比率を表す。次に、複比は比の比として現れ、2 つの点 C, D が線分に対してどのように位置しているかを表す。点 A, B, C, D が異なる限り、複比 (A, B; C, D) はゼロ以外の実数となる。それは次のように簡単に推測できる。
- (A, B; C, D) < 0 は、点 C, D の一方が点 A, B の間にあり、他方が点 A, B の間にない場合に限る。
- (A, B; C, D) = 1 / (A, B; D, C)
- (A, B; C, D) = (C, D; A, B)
- (A, B; C, D) ≠ (A, B; C, E) ↔ D ≠ E
6つの複比[編集]
4点を並べる方法は 4! = 4 × 3 × 2 × 1 = 24 通りだが、それらを順序付けられていない2つのペアに分割する方法は6通りしかない。したがって、4点は異なる交差比を6つのみ持つ。これらは次の関係式のようになる。
後述の非調和群を参照。
射影幾何学[編集]

複比は射影直線の射影変換によって保持されるという意味で射影不変量である。
特に、4つの点がR2の直線L上にある場合、それらの複比は、原点を選択や線上のスケールを選択に関わらず同じ値になるため well-defined な量である。
さらに {Li | 1 ≤ i ≤ 4} は、同じ点Qを通る平面上の4本の異なる直線である。次に、Qを通過しない任意の線Lは、4つの異なる点Piでこれらの線と交差する (LがLiに平行である場合、対応する交点は「無限遠」にある)。これらの点の(固定された順序で与えられる)複比は、線Lの選択に依存しないことがわかる。したがって、4本の線の組 {Li} の不変量である。
これは、LとL′がQを通過しない2つの線である場合、Qを中心とするLからL′への透視変換は、L上の4つの点の組 {Pi} からL′上の4つの点の組 {Pi′} 射影変換となることから理解できる。
したがって、直線の射影的自己同型の下での複比の不変性は、4つの直線 {Li} 上の4つの共線点 {Pi} の複比が、その線の選択から独立していることを意味する(実際には等価)。
同次座標での定義[編集]
同一線上にある4つの点がベクトルa, b, c, dによって同次座標で表され、 c = a + b および d = ka + b である場合、それらの複比はkである。[5]
非ユークリッド幾何学における役割[編集]
アーサー・ケイリーとフェリックス・クラインは、複比の非ユークリッド幾何学への適用を発見した。実射影平面の正則円錐曲線Cが与えられると、射影群G = PGL(3, R)内のそのスタビライザーGCはCの内部の点に推移的に作用する。ただし、点のペアに対するGCの作用には不変条件がある。実際、そのような不変量はすべて、適切な複比の関数として表現できる。[要出典]
双曲幾何学[編集]
明示的に円錐曲線を単位円とする。単位円内部の任意の2点 P, Q に対し、それらを結ぶ直線が円と交差する2点 X, Y を順が X, P, Q, Y となるように決める。このとき双曲平面のケイリー・クラインモデルにおけるPとQの間の双曲距離は、
のように表せる(曲率を -1 にするためには係数の 1/2 が必要である)。複比は射影変換の下で不変であるため、双曲線距離は円錐Cを保存する射影変換の下で不変であるということになる。
逆に、群Gは固定された双曲的距離で単位円盤の点(p, q)のペアのセットに推移的に作用する。
後に、アンリ・ポアンカレの影響もあり、円上の4つの複素数の複比が双曲線計量に使用された。円上にあるということは、メビウス変換の下で4つの点が4つの実点の像であることを意味するため、複比は実数となる。ポアンカレ半平面モデルとポアンカレの円板モデルは、複素射影直線における双曲幾何学の2つのモデルである。
これらのモデルは、 ケイリー・クライン計量の例である。
非調和群とクライン四群[編集]
複比は、次の4つの式のいずれかで定義できる。
これらは、次の(循環表記法で表現された)変数の順列によって異なる。
4つの変数の順列は、4つの変数の関数に対する対称群S4の作用と考えることができる。上記の4つの順列は複比を変えないため、この作用の下で複比のスタビライザーKを形成し、複比の軌道上の商群の有効な作用を成す。 Kの4つの順列は、S4のクラインの四元群を実現し、商は対称群S3と同形である。
したがって、4つの変数の他の順列は複比を変え、6要素の群の軌道である次の6つの値を与える。
λの関数とすると、これらはメビウス変換の例であり、関数の合成の下でメビウス群PGL(2, Z)を形成する。 6つの変換は非調和群として知られる部分群を形成し、これも S3に同型である。それらはPGL(2, Z)の捩れ元(楕円変換)である。すなわち、 , , はそれぞれ固定点 −1, 1/2, 2 を持つ位数2(つまり、調和複比の軌道)である。一方、とはPGL(2, Z)の位数3であり、それぞれが両方の「最も対称的な」複比の値を固定する。
非調和群はλ ↦ 1/λとλ ↦ 1 − λによって生成される。 {0, 1, ∞}に対するその作用は S3との同型を与える。また、前述の6つのメビウス変換[6]として実現することもでき、これは(整数エントリで定義されるため)任意の体上でS3の射影表現を生成し、(2つの項が1/−1のみが異なることはないため)常に忠実/単射である。 2元体上では射影直線は3点しか持たないため、この表現は同型であり、例外的な同型である。標数3では、これにより点 が安定し、これはであることから調和複比の軌道が1点のみであることに対応する。 3元体上では、射影線には4つの点しかなく、 であり、したがってこの表現は正確に調和複比のスタビライザーであり、点 のスタビライザーに等しい埋め込みが得られる。
例外的な軌道[編集]
λが特定の値のとき、対称性が高くなるため交差比の可能な値は6つより少なくなる。 λのこれらの値は、リーマン球面上のS3の作用の固定点に対応する(前述の6つの関数によって与えられる)。言い換えると、この順列群に非自明なスタビライザーを持つこれらの点に対応する。
固定点の最初の集合は{0, 1, ∞}である。ただし、点 A, B, C, D がすべて異なる場合、複比はこれらの値を取ることはできない。これらの値は、座標の1つのペアが互いに接近するときの極限値である。
固定点の2番目の集合は{−1, 1/2, 2}である。この状況は、古典的に調和複比と呼ばれるもので、射影調和共役で起こりうる。実数の範囲では、他に例外的な軌道はない。
複素数の範囲では、最も対称的な複比はである場合にみられる。これらは複比の唯一の2つの値であり、これらは順列の符号に従って作用する。
変換的アプローチ[編集]
複比は、直線の射影変換の下で不変である。複素射影線またはリーマン球の場合、これらの変換はメビウス変換として知られている。一般的なメビウス変換の形式は次のように表される。
これらの変換は、リーマン球に作用する群、メビウス群を形成する。
複比の射影不変性は、
すべてのメビウス変換が一般化された円を一般化された円にマッピングするという事実より、4つの点が共線または共円である場合にのみ複比が実数になる。
メビウス群の作用は、リーマン球の異なる点の三つ組の集合上で単純に推移的である。異なる点の任意の順序付き三つ組(z2, z3, z4)が与えられると、一意なメビウス変換f(z)が存在する。この変換は複比を用いて簡単に記述できる。(z, z2; z3, z4)は(f(z), 1; 0, ∞)に等しくなければならず、これはf(z)に等しいため、次の式が得られる。
複比の不変性の別の説明は、直線の射影変換の群が平行移動、相似性、乗法的反転によって生成されるという事実に基づいている。差zj − zkは、基礎体Fの定数aに対する平行移動、
の下で不変である。また、分割比はFの非ゼロ定数bに対する相似変換、
の下で不変である。したがって、複比はアフィン変換の下で不変である。
を得るために、アフィン線は、射影線P1(F) を形成する ∞ で示される無限遠の点によって拡張される必要がある。各アフィン写像 f : F → F は、点を無限遠に固定するP1(F) のそれ自体への写像に一意に拡張できる。写像Tは 0 と ∞ を交換する。射影群はTによって生成され、アフィン写像はP1(F) に拡張される。 F = C 、すなわち複素平面の場合、これはメビウス群になる。複比もTの下で不変であるため、P1(F)のそれ自体への射影写像の下で不変である。
座標の説明[編集]
複素数点をベクトルとして書き、 と定義し、との内積をと表記するとき、複比の実部は次の式で与えられます。
これは、反転などの2次元特殊等角写像の不変量である。
虚部は2次元の外積を使用する必要がある。
環のホモグラフィ[編集]
複比の概念は、加法、乗法、反転の環演算にのみ依存する(ただし、特定の元の反転は環ではその限りではない)。複比へのひとつのアプローチは、指定された3点を 0、1、無限大 にするホモグラフィとして解釈することである。逆数に関する制限の下で、環上の射影直線による環操作を使用してそのような写像を生成することが可能である。 4 点の複比は、4点目でのこのホモグラフィの評価である。
微分幾何学の視点[編集]
この理論は、4つの点が近接するにつれて、微分計算の側面を帯びる。これは、シュワルツ導関数の理論につながり、より一般的には射影接続の理論につながる。
高次元の一般化[編集]
複比は、点の構成の他の幾何学的特性、特に共線性により、単純な方法ではより高い次元に一般化されない。構成空間はより複雑であり、点の異なるk-組は一般化位置にない。
射影線の射影線型群は3推移的(任意の3つの異なる点を他の任意の3 点に写像できる)であり、実際には単純な3推移的である(任意の三つ組を別の三つ組に取る一意の射影写像がある)が、したがって、複比は4つの点の集合の一意の射影不変量であり、高次元には基本的な幾何学的不変量がある。 n空間の射影線型群は(n + 1)2 − 1次元を持つ(であり、1つの次元を削除する射影化であるため)が、他の次元では、射影線型群は2推移性のみである。これは、3つの共線上の点を3つの共線上の点に写す必要があるためである(これは、射影線の制限ではない)。したがって、n2点の一意の不変量を提供する一般化交差比は存在しない。
共線性は、維持する必要がある点の構成の唯一の幾何学的特性ではない。例えば、 5つの点は円錐曲線を決定するが、6つの点は一般に円錐曲線上にないため、「点の6つ組が円錐曲線上にあるか否か」も射影不変量となる。一般化位置での点の軌道を調べることができる(「一般化位置」の直線では区別することと同等だが、より高い次元では、議論したように幾何学的な考慮が必要である)が、上記のように、これはより複雑で情報が少なくなる。
ただし、アベル・ヤコビ写像とシータ関数を用いた、種数が正のリーマン面への一般化が存在する。
関連項目[編集]
脚注[編集]
- ^ A theorem on the anharmonic ratio of lines appeared in the work of Pappus, but Michel Chasles, who devoted considerable efforts to reconstructing lost works of Euclid, asserted that it had earlier appeared in his book Porisms.
- ^ Alexander Jones (1986) Book 7 of the Collection, part 1: introduction, text, translation ISBN 0-387-96257-3, part 2: commentary, index, figures ISBN 3-540-96257-3, Springer-Verlag
- ^ Howard Eves (1972) A Survey of Geometry, Revised Edition, page 73, Allyn and Bacon
- ^ W.K. Clifford (1878) Elements of Dynamic, books I,II,III, page 42, London: MacMillan & Co; on-line presentation by Cornell University Historical Mathematical Monographs.
- ^ Irving Kaplansky (1969). Linear Algebra and Geometry: A Second Course. ISBN 0-486-43233-5
- ^ Chandrasekharan, K. (1985). Elliptic Functions. Grundlehren der mathematischen Wissenschaften. 281. Springer-Verlag. p. 120. ISBN 3-540-15295-4. Zbl 0575.33001
参考文献[編集]
- Lars Ahlfors (1953,1966,1979) Complex Analysis, 1st edition, page 25; 2nd & 3rd editions, page 78, McGraw-Hill ISBN 0-07-000657-1 .
- Viktor Blåsjö (2009) "Jakob Steiner’s Systematische Entwickelung: The Culmination of Classical Geometry", Mathematical Intelligencer 31(1): 21–9.
- John J. Milne (1911) An Elementary Treatise on Cross-Ratio Geometry with Historical Notes, Cambridge University Press.
- Dirk Struik (1953) Lectures on Analytic and Projective Geometry, page 7, Addison-Wesley.
- I. R. Shafarevich & A. O. Remizov (2012) Linear Algebra and Geometry, Springer ISBN 978-3-642-30993-9.
外部リンク[編集]
- 『複比の定義と複比が不変であることの証明』 - 高校数学の美しい物語
- MathPages – Kevin Brown explains the cross-ratio in his article about Pascal's Mystic Hexagram
- Cross-Ratio at cut-the-knot
- Weisstein, Eric W. "複比". mathworld.wolfram.com (英語).
- “The Cross Ratio” (video). youtube. Brady Haran. 2021年12月12日時点のオリジナルよりアーカイブ。2018年7月6日閲覧。











![{\displaystyle {\begin{aligned}&(A,B;C,D)=(B,A;D,C)=(C,D;A,B)=(D,C;B,A)=\lambda \\[6pt]&(A,B;D,C)=(B,A;C,D)=(C,D;B,A)=(D,C;A,B)={\frac {1}{\lambda }}\\[6pt]&(A,C;B,D)=(B,D;A,C)=(C,A;D,B)=(D,B;C,A)=1-\lambda \\[6pt]&(A,C;D,B)=(B,D;C,A)=(C,A;B,D)=(D,B;A,C)={\frac {1}{1-\lambda }}\\[6pt]&(A,D;B,C)=(B,C;A,D)=(C,B;D,A)=(D,A;C,B)={\frac {\lambda -1}{\lambda }}\\[6pt]&(A,D;C,B)=(B,C;D,A)=(C,B;A,D)=(D,A;B,C)={\frac {\lambda }{\lambda -1}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d183595870a6d516df017a1ae4c6af3bd142b15)





&={\frac {1}{1-\lambda }}&(A,C;B,D)&=1-\lambda \\[6pt](A,D;C,B)&={\frac {\lambda }{\lambda -1}}&(A,D;B,C)&={\frac {\lambda -1}{\lambda }}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/056eb286b7321522447c94b426f0c4cf48ee09b9)







![{\displaystyle -1=[-1:1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24adc46c179c53ef270f071518cb7d308300fdeb)














![{\displaystyle {\overrightarrow {x}}_{n}=[\Re (z_{n}),\Im (z_{n})]^{\rm {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/470f3991f5806e33b77e9e9695b4a9f36bbafc19)






![{\displaystyle a\times b=[a,b]=a_{2}b_{1}-a_{1}b_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f245d88996a813e2730e805cf059f1162ec30464)
![{\displaystyle C_{2}={\frac {(x_{12},x_{14})[x_{34},x_{23}]-(x_{43},x_{23})[x_{12},x_{34}]}{|x_{23}|^{2}|x_{14}|^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0702314588cb44e101aa76943658393dca6b1ddc)

