従円と周転円
従円(導円)と周転円(じゅうえん(どうえん)としゅうてんえん、deferent and epicycle)は、古代ギリシアの天動説的な天文学で、月や太陽、惑星などの運行の速さや方向の変化を説明するために導入された、数学的な概念である。従円-周転円理論では、天体の運動は、大きな円(従円、あるいは導円)の円周を中心とする小さな円(周転円)の円周上を運動するという円軌道の組み合わせで説明された。(この組み合わせで生成される運動の軌跡をエピトロコイドという。)
紀元前3世紀の終わり頃のアポロニウスは、惑星の順行・逆行の説明に既にこれを用いていた。また、ヒッパルコスやプトレマイオスの数理天文学で非常に重要な役割を果たし、精密な天体の方位の計算を可能にした。
従円-周転円は、古代ギリシア天文学とともに広まり、中世イスラム世界、中世後期のヨーロッパ、また5世紀以降のインドでも用いられた。中世前期のヨーロッパにおいても、基本的な考え方は知られていた。
アリストテレスの宇宙論では、天体は地球を中心に回転するとされ、周転円のような、地球を中心としない回転は想定していなかった。そこで、周転円を用いた理論が、どの程度実在する宇宙を反映しているのか、また数理天文学と自然学との関係について、古代末期から中世にかけて様々な議論があった。中には、従円や周転円を用いずに、地球中心の回転のみで天体の動きを説明しようとする試みもあった。
なお、コペルニクスの地動説やティコ・ブラーエの部分的な太陽中心説も、この理論を用いている。
惑星の理論[編集]
プトレマイオス『アルマゲスト』によれば、紀元前3世紀の終わり頃の小アジアのペルガ出身の数学者アポロニウスは、既に従円と周転円を惑星の順行・逆行の説明に用いていた。先行するエウドクソスの同心球説に比較すると、数値的な分析にも向いており、火星などの明るさの変化を距離の変化として説明することができるといった長所があった[1]。
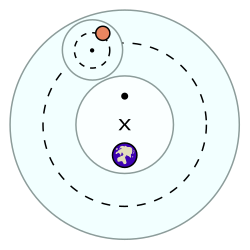
惑星の理論を作るにあたって、プトレマイオスは、惑星の運動に太陽との相対的な位置で決まる成分があることを指摘して(『アルマゲスト』IX.5)、太陽と関係なく決まる成分と分離し、片方を従円(導円)に、残りの片方を周転円に割り振った。現代から見れば、惑星の公転と地球の公転への分離に近いことをしていたことになる[2]。上図において、惑星(黄色)は周転円(小さい円)に沿って等速回転し、周転円の中心は、従円(大きい円)に沿って動く。回転方向は、いずれも反時計回りである。
逆行と順行の境目で惑星が一瞬停止する留は、古代メソポタミアでも大きな関心が寄せられ、観測や理論的な考察の対象になったが、留の前後でも惑星の動きは非常にゆっくりであるため、精確な決定は難しかった。プトレマイオス『アルマゲスト』XIIでは、アポロニウスの留が起る点を幾何学的に求める理論が紹介され、続いて各々の外惑星に当てはめている。
実際には惑星はケプラーの法則に従って楕円運動し、等速円運動ではない。両者の差を埋めるために、『アルマゲスト』では従円に離心円、すなわち地球を中心としない円を用い、また回転速度をエカントを用いて調節した[2]。上図のxが従円の中心であるが、地球(青い点)はややずれたところにあり、回転速度はエカント(黄色い点)から見て等速に見えるように調整されている。
従円も周天円も、黄道とほぼ平行にされていた。これは、惑星が黄道に近いエリア(獣帯)でのみ運動していることを説明している。ただし、獣帯の中での黄緯の変化を説明するため、従円や周天円は黄道に対してやや傾いており、その傾きは変化するとされたり(『アルマゲスト』)、一定の値で固定(プトレマイオス『惑星仮説』、アーリヤバタ『アーリヤバティーヤ』など)されたりした。
太陽・月の理論[編集]
ヒッパルコスやプトレマイオスは、天体の速度の変化を表す機構として、従円-周転円のほかに、離心円(地球でない点を中心とする円)を導入し、太陽の理論に用いている。この理論では、太陽は地球と異なる点を中心に等速回転するため、地球から見ると速度が変化しているように見え、太陽の年周運動の速さが、冬至付近と夏至付近でことなることを説明できる。一方、プトレマイオス『アルマゲスト』III.3で指摘されるように、従円-周転円でも、全く同じ運行速度の変化を説明できる。プトレマイオスは、どちらの理論を取るべきかを明瞭にしてない。
『アルマゲスト』の月の理論は非常に複雑なことで有名だが、第IV巻では、まず最初に満月と新月の近辺(つまり日食や月食が起りうる時)でのみ当てはまる、従円ー周転円による簡単な理論を展開する(後で徐々に複雑化)。ただし惑星の場合とことなって、周転円の回転方向は従円と逆方向である。このとき、離心円ではなく従円-周転円の理論を採用した理由として、前者では運行速度が様々な点で最大になりうることを説明できない、としている。
「離心円理論」[編集]
すでに述べたように、離心円は従円-周転円で置き換えられる。逆に、惑星の逆行などを考えれば明らかなように、従円-周転円で作られる運動は、必ずしも離心円に沿った等速回転で表すことは出来ない。一方、プトレマイオスは、離心円の中心を地球を中心に回転させる理論も考え、「離心円理論(離心円の仮説)」とよんだ。これは現代から見れば、単に従円と周転円を入れ替えただけであるから、当然、従円-周転円理論と同じ運動を表現できる。
しかし、従円-周転円理論と「離心円理論」の関係についての『アルマゲスト』の説明は、複数の個所に現れ(III.3,IV.5,IX.5,XII.I)、一貫していない。IV.5では、月の「第一の理論」、すなわち従円ー周転円に基づく理論が「離心円理論」でも表現可能であることを示す。ところが、IX.5では、惑星の速度変化の性質から、惑星理論は従円-周転円理論でなければならないと結論する。さらに、外惑星の留を扱うXIIでは、また一転して「離心円理論」による置き換えが外惑星については可能で、ただし内惑星では不可能だとする[3]。
だが、この問題が注意を引いたのは、ずっと後のことであった。そもそも「離心円理論」は、『アルマゲスト』でも実際の天体の分析では使われず、またプトレマイオスの宇宙論の書『惑星仮説』でも取り上げられていない。そのため、中世においても、「離心円理論」が正面から取り上げられたことは、ほとんどなかった。
この『アルマゲスト』の混乱が指摘・修正されるのは、やっと15世紀のクシュチー(en:Ali Qushji)やレギオモンタヌスになってからであった[4]。コペルニクスがプトレマイオス体系の書き換えを通じて地動説に至る際に、この円の入れ替えが重要な役割を果たしたと推測されている。また、インドにおいては、14-15世紀のケーララ学派のニーラカンタが内惑星と外惑星を統一的に扱う理論を作る際に用いられた。
天球としての実体化[編集]
アリストテレスは、天体が透明で硬い球(天球)に張り付き、天球の回転によって運ばれるとした。プトレマイオスも、『惑星仮説』の中で、周転円や従円に天球としての実体を与えた。天体は周転円と中心が同じで天体を包む球に、周転円は従円と中心が同じで周転円を包むに、各々張り付いている。そして、各々の球が回転する。
このような実体が与えられたため、現代からみるとほぼ同値である「従円-周転円理論」と「離心円理論」も、物理的にかなり異なる理論だと捉えられた。中世の後半期、この物理的な実体を徹底して突き詰め考える傾向が、イスラム圏でもヨーロッパでも現れ、結果的にはプトレマイオス理論の動揺に繋がった。科学史家スワードローは、コペルニクスが太陽中心説に至る際、「天球は固体なので、天体の軌道に交錯が許されない」という考えは非常に重要な役割を果たした、と推測している。
その一方、やや後のティコ・ブラーエは、彗星の軌道の観測から、この原則が破綻していることを確信し、自らの理論では躊躇なく火星と太陽の天球を交錯させている。この発見を受けて、それ以降の天動説では天球を液体とする説が現れるようになった。
ただし、インドに於いては、円を天球として実体化することはされず、例えば円の半径が回転しながら変化する理論なども考えられた。
批判[編集]
アリストテレス『天体論』では、天体は地球を中心にして等速回転するとされた。しかし、周転円や離心円の回転は地球の中心ではない。古代末期のプロクロスがすでにこの問題を指摘しており、中世においても広く認識されていた。ただし、この問題にどのように取り組むべきかについては、様々な考えがあった。例えば、プロクロスは、「従円-周転円理論でも離心円理論でも同じ現象が説明できる」ことなどを挙げ、自然学と数学的な理論の差を埋めることに、あまり希望を抱いていない。
また、物理的な宇宙論と矛盾のない数理天文学を目指すものの中でも、従円-周転円や離心円に対する立場は様々であった。例えば、周転円も離心円も等速回転であれば問題ないとするもの(「マラーガ学派」およびコペルニクス)が居る一方、従円-周転円は認めるが離心円を嫌うもの(イブン・シャーティル)や、逆に離心円は認めるが従円-周転円は不可とする者(イブン・バーッジャ)がいた。
さらに、12世紀スペインのイブン・ルシュドは離心円も従円-周転円も拒否し、「今の天文学は、計算には合うが、存在するものには合わない」として真の天文学の探求を後世に託し、アル・ビトゥルージは新たな同心球説を発展させた。これらの議論は主に欧州に伝わり、様々な議論をひきおこした。
同心球説とは異なる立場からの反論として、ユダヤ人学者ゲルソニデスは、『アルマゲスト』の周転円を用いる理論では、月のみかけの大きさ(視直径)や、常に同じ面を地球に向けていることを説明できないとした。そして、従円-周転円理論を用いず離心円のみに基づく月の理論を作り、自らの観測データと比較し、『アルマゲスト』の理論よりもよく合うとした[5]。
フーリエ変換との関係[編集]
中世の後半期に、中東の「マラーガ学派」(トゥスィーやウルディーら)や、コペルニクスらはエカントによる回転速度の変化を嫌い、等速円運動の重ね合わせで置き換えた。この場合は、周転円をいくつも重ね合わせる必要がある。このような理論は、惑星の軌道のフーリエ変換を有限の項で打ち切ったものと思うことが出来る。すなわち、閉じたループに沿った運動を、実数から複素数への滑らかで有界な関数と捉えて、フーリエ変換をすると、周転円による近似の系列を導くことができる。
脚注[編集]
- ^ 惑星や恒星のような、小さく見える天体については、見かけの明るさには、(光っている部分の)見かけの大きさ(面積)に比例すると考えられていた。後者は距離の2乗に反比例する。 惑星が自ら発光するのか、或いは月のように太陽に照らされて光るのかについては、プトレマイオスは何も言及していない。中世には両方の説があった。
- ^ a b ただし、周転円に割り振られた軌道の円運動からのずれの一部は、従円の離心率に反映させられた。Mozaffari SM. The Orbital Elements of Venus in Medieval Islamic Astronomy: Interaction Between Traditions and the Accuracy of Observations. Journal for the History of Astronomy. 2019;50(1):46-81, 特にpp.49-50。
- ^ アポロニウスによる留の条件は、従円-周転円および「離心円理論」の両方で述べられている。
- ^ Shank 2017および、Ragep, F. J., 'Ali Qushji and Regiomontanus: eccentric transformations and Copernican Revolutions, Journal for the History of Astronomy (ISSN 0021-8286), Vol. 36, Part 4, No. 125, p. 359 - 371 (2005)
- ^ Goldstein, Bernard R. “Theory and Observation in Medieval Astronomy.” Isis, vol. 63, no. 1, 1972, pp. 39–47. なお、彼の月の理論では、月は離心円上をやや複雑な規則に従って回転するのであって、等速円運動ではない。
参考文献[編集]
- Neugebauer, O., A History of Ancient Mathematical Astronomy, Springer, 1975
- Pedersen, Olaf:A Survey of the Almagest, Odense University Press,Odense, 1974
- Ptolemy, Claudius. Ptolemy’s Almagest. Trans. G.J. Toomer. London: Duckworth,1984.
- Ragep, F. J., 'Ali Qushji and Regiomontanus: eccentric transformations and Copernican Revolutions, Journal for the History of Astronomy (ISSN 0021-8286), Vol. 36, Part 4, No. 125, p. 359 - 371 (2005)
- Saliba, G., (1996) Arabic planetary theories after the eleventh century AD :in Rashed, ed. (1996) Encyclopedia of the History of Arabic Science, vol.1. Routledge, pp. 59-128, arxiv.org
- Shank, Michael H. “Regiomontanus and Astronomical Controversy in the Background of Copernicus.” Before Copernicus: The Cultures and Contexts of Scientific Learning in the Fifteenth Century, edited by Rivka Feldhay and F. Jamil Ragep, McGill-Queen's University Press, Montreal; Kingston; London; Chicago, 2017, pp. 79–109.
- 大橋由紀夫 離心円と周転円の話 - 日本科学史学会
