ウェーブレット

数学におけるウェーブレット(英語: wavelet)、ウェーブレット解析、ウェーブレット変換とは、マザーウェーブレットと呼ばれる有限長波形（もしくは速やかに減衰しながら振動する波形）による信号表現である。信号表現は入力信号に合致するようなウェーブレット波形の拡大縮小（スケーリング）・平行移動（シフト）により行われる。より正確には、この信号表現はウェーブレット系列と呼ばれ、これは2乗可積分関数のヒルベルト空間における完備直交基底関数集合を用いた座標表現である。

JPEG 2000で使われているウェーブレットは双直交ウェーブレットであり、ウェーブレット系列の座標は異なる2つの基底関数集合を用いて計算されるため、注意を要する。

歴史

ウェーブレットの発展は、20世紀初頭のハンガリー人数学者アルフレッド・ハールによるいくつかの断片的な考察に基づく。ガーボル・デーネシュによるその後の研究でガボール・アトムが得られた。ガボール・アトムはウェーブレットと似た形で構成され、似た目的に応用された。ウェーブレット理論への大きな貢献のひとつは、1975年のジョージ・ツワイクによる連続ウェーブレット変換（初期には cochlear 変換と呼ばれていて、耳の音に対する反応を研究していたときに発見された。） の発見である。

ウェーブレットの概念は、1975年にエルフで石油探査をしていたフランス人地球物理学者ジャン・モーレーが発見した。1981年、モーレーは クロアチア系フランス人物理学者アレックス・グロスマンとの共同研究から連続ウェーブレット変換の定式化（Goupillaud）を行なった。彼らはフランス語で"小さい波"を意味するondeletteという言葉を用いていたが、少し後に英語に翻訳された際に"onde"は"wave"と訳されてウェーブレット("wavelet")という用語が誕生した。

その後のウェーブレット理論における大きな貢献には、Strombergによる離散ウェーブレット変換における初期研究(1983)、イングリッド・ドブシーによるコンパクト台を持つ直交ウェーブレット(1988)、Mallatによる多重解像度解析に関する提案(1989)、Delpratによる連続ウェーブレット変換における時間-周波数変換(1991)、Newlandによるハーモニックウェーブレット変換など、枚挙にいとまがない。

年表

• 1909年: 最初のウェーブレット (Haarによるハールウェーブレット)
• 1950年代以降: Jean Morlet , Alex Grossman
• 1980年代以降: Yves Meyer, Stephane Mallat, Ingrid Daubechies, Ronald Coifman, Victor Wickerhauser

ウェーブレット理論のアウトライン

ウェーブレット理論は、いくつかの異なる目的で応用される。 全てのウェーブレット変換は、時間周波数表現であると考えられるが、調和解析とも関係がある。

ウェーブレット変換は、大きく連続ウェーブレット変換(CWT)と離散ウェーブレット変換(DWT)に分類される。これらの違いは、CWTでは可能な全てのスケールとシフトが用いられるのに対して、DWTでは一部分のみが使われることにある。

連続ウェーブレット変換は、ハイゼンベルクの不確定性原理に支配されている。同様に、離散ウェーブレットにおいても不確定性原理は考慮されなければならない。

多くの場合に有用である離散ウェーブレット変換は、有限インパルス応答(FIR)フィルタで構成されるフィルタバンクである。

ウェーブレット変換は３つに分類されることが多い。連続ウェーブレット変換、離散ウェーブレット変換、多重解像度解析(MRA)による離散ウェーブレット変換である。以下、この３つについて解説する。

連続ウェーブレット変換

連続ウェーブレット変換においては、有限なエネルギーを持った信号は、連続な周波数バンドの群（もしくは$L^2(\R)$関数空間の一部) として投影される。得られた周波数成分は、適切な積分によって元の信号を再構成することができる。

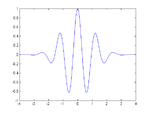
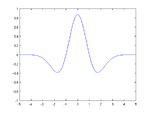
部分空間の群は、スケール1の部分空間を拡大縮小（スケール）して生成されたものである。この部分空間は、１つの関数すなわちマザーウェーブレット$\psi\in L^2(\R)$をシフトすることによって生成される。 一般的なマザーウェーブレットの例は以下のとおりである。

Meyer

Morlet

Mexican Hat

スケールaの部分空間は、以下の式で生成される。(これはベビーウェーブレットと呼ばれることがあるがあまり一般的ではない)

$\psi_{a,b} (t) = \frac1{\sqrt a }\psi \left( \frac{t - b}{a} \right)$

ただし、aは正の実数でありスケールを決定する。bは任意の実数でありシフトを決定する。(a,b)のペアは、$\R_+\times \R$の上半面において定義される。

関数xをスケールaの部分空間へ投影すると、以下の式で示される。

$x_a(t)=\int_\R WT_\phi\{x\}(a,b)\cdot\psi_{a,b}(t)\,db$

但し、WTはウェーブレット係数である。

$WT_\phi\{x\}(a,b)=\langle x,\psi_{a,b}\rangle=\int_\R x(t)\overline{\psi_{a,b}(t)}\,dt$.

信号xの解析のためには、ウェーブレット係数をスケーログラムにする。

離散ウェーブレット変換

詳細は「離散ウェーブレット変換」を参照

全てのウェーブレット係数を使って信号を解析することは実用上不可能である．信号を対応するウェーブレット係数から再構成することは，上半面の離散部分集合さえ取り出せば十分可能だと思うだろう．その一つとして実数パラメータa>1，b>0によるアフィン系がある．対応する半面の離散部分集合は，全ての点$(a^m, n\,a^m b)$を含む（$m,n\in\Z$）．対応するベビーウェーブレットは以下で与えられる．

$\psi_{m,n}(t)=a^{-m/2}\psi(a^{-m}t-nb)$.

式

$x(t)=\sum_{m\in\Z}\sum_{n\in\Z}\langle x,\,\psi_{m,n}\rangle\cdot\psi_{m,n}(t)$

による有限エネルギーを持つ任意の信号xの再構成のための十分条件は，関数群$\{\psi_{m,n}:m,n\in\Z\}$が$L^2(\R)$のタイトフレームを形作ることである．

多重解像度解析による離散ウェーブレット変換

各種あるウェーブレット変換の離散化の全ての方法において、上半面上の各有界矩形領域は有限個の係数のみを持つ。しかし、各係数を求めるためには積分の評価が必要となる。このような数値的な複雑さを避けるために、ファザーウェーブレットと呼ばれる補助関数 $\phi\in L^2(\R)$ が利用される。このとき a は整数でなければならない。例えば典型的な係数として a=2、b=1 が用いられる。最も有名なファザー・マザーウェーブレットの組としてドブシーの4タップウェーブレットがある。

D4 wavelet

マザー・ファザーそれぞれのウェーブレットから部分空間

$V_m=\operatorname{span}(\phi_{m,n}:n\in\Z)$, where $\phi_{m,n}(t)=2^{-m/2}\phi(2^{-m}t-n)$

と

$W_m=\operatorname{span}(\psi_{m,n}:n\in\Z)$, where $\psi_{m,n}(t)=2^{-m/2}\psi(2^{-m}t-n)$.

が構成される．これらより、系列

$\{0\}\subset\dots\subset V_1\subset V_0\subset V_{-1}\subset\dots\subset L^2(\R)$

は $L^2(\R)$ の多重解像度解析を形成することになり、また部分空間 $\dots,W_1,W_0,W_{-1},\dots\dots$ は上の系列の直交する差分、つまり $W_m$ は $V_{m-1}$ 中にある $V_m$ の直交補空間となる。サンプリング定理と同様に、sampling distance $2^m$ の空間 $V_m$ は 0 から $2^{-m-1}$の周波数帯域をほぼカバーすることになる。また $W_m$ は直交補空間として帯域 $[2^{-m-1},2^{-m}]$ を大まかにカバーする。

このような包含と直交の関係より，2つの恒等式

$h_n=\langle\phi_{0,0},\,\phi_{1,n}\rangle$ and $\phi(t)=\sqrt2 \sum_{n\in\Z} h_n\phi(2t-n)$

と

$g_n=\langle\psi_{0,0},\,\phi_{1,n}\rangle$ and $\psi(t)=\sqrt2 \sum_{n\in\Z} g_n\phi(2t-n)$.

を満たす系列 $h=\{h_n\}_{n\in\Z}$ と $g=\{g_n\}_{n\in\Z}$ が存在することになる。

2番目の恒等式はファザーウェーブレット $\phi$ の洗練条件と呼ばれる。これらの恒等関係は高速ウェーブレット変換アルゴリズムの土台となっている．

マザーウェーブレット

実応用での効率性を考えると、マザー（プロトタイプ）ウェーブレット（関数）はコンパクトサポートの連続微分可能関数であることが望ましい。しかし、（連続WTにおける）解析的であることの要求と、理論的な理由から、一般的にウェーブレット関数は 空間 $L^1(\R)\cap L^2(\R)$ の部分空間から選ばれる。これは絶対値積分可能かつ2乗積分可能な可測関数の空間である。

$\int_{-\infty}^{\infty} |\psi (t)|\, dt <\infty$ and $\int_{-\infty}^{\infty} |\psi (t)|^2 \, dt <\infty$.

この関数空間では必ずゼロ平均と二乗ノルムの条件が定式化できる。

$\int_{-\infty}^{\infty} \psi (t)\, dt = 0$ （ゼロ平均の条件）

$\int_{-\infty}^{\infty} |\psi (t)|^2\, dt = 1$ （二乗ノルム正規の条件）

$\psi$ が 連続ウェーブレット変換（正確な議論はリンク先参照）のウェーブレットであるためには、マザーウェーブレットは安定な逆変換を持つための許容性の規範（簡単に言うとこれは半微分可能性のようなもの）を満たさなければならない。

離散ウェーブレット変換における最低限満たさなければならない条件として、ウェーブレット系列はLp空間 $L^2(\R)$ 中の単位元でなければならない。離散WTのほとんどの構成は多重解像度解析を用いており、この場合ウェーブレットはスケール関数により決定される。このスケール関数自体が汎関数方程式である。

多くの場合において $\psi$ をvanishing moments を表すより大きい数字 M の連続関数、つまり全ての整数 m<M について以下の式を満たす関数に限定することは有用である。

$\int_{-\infty}^{\infty} t^m\,\psi (t)\, dt = 0$

マザーウェーブレットは、$a$の因数による拡大縮小（スケール）と、$b$ の因数による平行移動（シフト）により、（Morlet によるオリジナルの定式化のように）以下のように与えられる。

$\psi _{a,b} (t) = {1 \over {\sqrt a }}\psi \left( {{{t - b} \over a}} \right)$.

連続WTでは、(a,b) のペアは全半平面 $\R_+\times=R$ 上で変化する。また離散WTでは、このペアは、affine群とも呼ばれる離散部分集合上で変化する。

これらの関数はたびたび（連続）変換の基底関数という誤った捉え方をされる。事実、連続フーリエ変換にあるような基底は、連続ウェーブレット変換にはみあたらない。時間周波数解釈では少し違う定式化が使用される（Delpratによる）。

フーリエ変換との比較

ウェーブレット変換は、三角関数の級数表現のフーリエ変換としばしば比較される。主な違いは、ウェーブレット変換は時間と周波数の両方の成分を局在化するが、標準的なフーリエ変換は周波数成分だけを局在化することである。短時間フーリエ変換も時間と周波数の両方を局在化できるが、時間周波数分解能に問題がある。一方、ウェーブレット変換ではしばしば多重解像度解析という、より良い表現が用いられる。

また、離散ウェーブレット変換の計算量はO(N)であり、高速フーリエ変換のO(N log N)に比べて小さい(ここで、Nはデータの大きさである)。

ウェーブレットの決定

ウェーブレット（およびウェーブレット族）の決定には様々な方法がある。

スケーリングフィルター

ウェーブレットはもっぱらスケーリングフィルタ g により決定づけられる。これは長さ 2N で和が 1 となる有限インパルス応答(FIR) の低域通過フィルタである。双直交ウェーブレットでは、分解と再合成のフィルタが別々に決定される。

分析では、高域通過フィルタは低域通過フィルタの QMF として計算され、再合成フィルタは分解フィルタの時間反転である。

例えば、ドブシー・ウェーブレットとSymletウェーブレットは、スケーリングフィルタで定義することができる。

スケーリング関数

ウェーブレットは、ウェーブレット関数$\psi (t)$(マザーウェーブレット)とスケーリング関数$\phi (t)$(ファザーウェーブレット)から定義される。

実際のところウェーブレット関数は帯域通過フィルターであり、それぞれの水準の半分の帯域幅でスケールされている。これによって、全てのスペクトルを扱うために無限の水準が必要となる問題が生じる。スケーリング関数を用いれば、最低限の水準で全てのスペクトルを扱うことができる。詳細な説明は[1]にある。

コンパクトサポートをもつウェーブレットでは、$\phi (t)$は有限長であり、スケーリングフィルターgと同等である。

例えば、Meyerウェーブレットは、スケーリング関数で定義することができる。

ウェーブレット関数

ウェーブレットはウェーブレット関数$\psi (t)$のような時間領域表現をただ一つ持つ。

例えば、Mexican hat waveletは、ウェーブレット関数で定義することができる。 いくつかの連続ウェーブレットのリストを参照。

応用

大まかに、DWTはデータ圧縮に使われる一方でCWTは信号解析に使われる。その結果として、DWTは工学と計算機科学において一般的に使われ、CWTは科学研究においてもっともよく使われている。ウェーブレット変換は、現在非常に多くの様々な用途に、しばしば従来のフーリエ変換を置き換えて使用されている。分子動力学、第一原理計算、宇宙物理学、密度行列局在、地震地球物理学、光学、乱流そして量子力学を含む、物理学の多くの分野でこのパラダイムシフトが起こった。この変化が起こった他の分野は画像処理、血圧、心拍やECGの解析、DNA解析、タンパク質解析、気候学、一般的な信号処理、音声認識、コンピュータグラフィックスそしてマルチフラクタル解析である。コンピュータビジョンや画像処理において、尺度空間表現やガウス微分オペレータの概念は正規化された多重スケール表現の一つであると考えられている。

ウェーブレットはデータ圧縮の分野でも用いられる。デジタル信号処理における他の時間-周波数変換と同様、ウェーブレット変換は(たとえば画像などの)圧縮されていないデータに対し適用でき、その後圧縮処理がなされることで、結果として効果的なデータ圧縮を実現できる。JPEG 2000はウェーブレットを利用した画像形式の一つである。ウェーブレットを利用したデータ圧縮についてはウェーブレット圧縮を参照されたい。

様々なウェーブレット変換

異なる用途に応じて、多くのウェーブレット変換が存在する。以下にその一例を列挙するが、すべてのウェーブレット変換についてのリストはウェーブレット変換の一覧を参照されたい。

• 連続ウェーブレット変換 (CWT)
• 離散ウェーブレット変換 (DWT)
• 高速ウェーブレット変換 (FWT)
• Wavelet packet decomposition (WPD)
• Stationary ウェーブレット変換 (SWT)

ウェーブレット一覧

離散ウェーブレット

• Beylkin (18)
• Coiflet (6, 12, 18, 24, 30)
• ドブシー・ウェーブレット (2, 4, 6, 8, 10, 12, 14, 16, 18, 20)
• Cohen-Daubechies-Feauveauウェーブレット (CDF N/PまたはDaubechies双直交ウェーブレットとして参照されることがある)
• ハールウェーブレット
• Symletウェーブレット

連続ウェーブレット

• Mexican hat wavelet
• Hermitian wavelet
• Hermitian hat wavelet
• Complex mexican hat wavelet
• Morlet wavelet
• Modified Morlet wavelet
• Beta wavelet
• Hilbert-Hermitian wavelet

関連項目

• Chirplet変換
• Curvelet
• フィルタバンク
• 非整数次フーリエ変換
• 多重解像度解析
• 短時間フーリエ変換
• 尺度空間
• 超広帯域ラジオはウェーブレットを送信する。

参考文献

• Paul S. Addison, The Illustrated Wavelet Transform Handbook, Institute of Physics, 2002, ISBN 0-7503-0692-0
• Ingrid Daubechies, Ten Lectures on Wavelets, Society for Industrial and Applied Mathematics, 1992, ISBN 0-89871-274-2
• P. P. Vaidyanathan, Multirate Systems and Filter Banks, Prentice Hall, 1993, ISBN 0-13-605718-7
• Mladen Victor Wickerhauser, Adapted Wavelet Analysis From Theory to Software, A K Peters Ltd, 1994, ISBN 1-56881-041-5
• Gerald Kaiser, A Friendly Guide to Wavelets, Birkhauser, 1994, ISBN 0-8176-3711-7

外部リンク

• Wavelets made Simple
• Wavelet Digest
• Course on Wavelets given at UC Santa Barbara, 2004
• Amaras Wavelet Page
• Wavelet Posting Board
• The Wavelet Tutorial by Polikar
• OpenSource Wavelet C Code
• An Introduction to Wavelets
• Wavelets for Kids (PDF file) (introductory)
• Link collection about wavelets
• List of Wavelet resources, libraries and source codes
• Wavelet forums (French) Wavelet forum (English)
• "Biorthogonal sinc wavelets"
• Gerald Kaiser's acoustic and electromagnetic wavelets
• A really friendly guide to wavelets
• Advanced Signal Processing Toolkit - Commercial software from National Instruments for wavelet-based analysis and processing in LabVIEW