ピタゴラス数
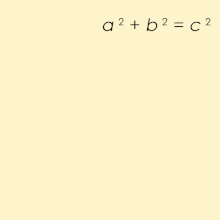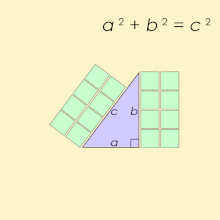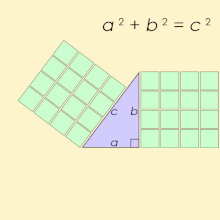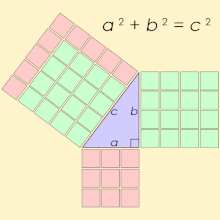
ピタゴラス数、あるいはピタゴラスの三つ組数 (英: Pythagorean triple)とは、a2 + b2 = c2 を満たす3つの自然数の組 (a, b, c) のことである。これはピタゴラスの定理に由来しており、直角三角形の3辺の長さでいずれも自然数であるものを意味する。3辺のうちある2辺が整数でも残りの辺が整数になるとは限らずその場合無理数となってしまうことから、ピタゴラス数のリストは興味の対象となる。
最小のピタゴラス数は (3, 4, 5) である。
(a, b, c) がピタゴラス数ならば
- (2a, 2b, 2c), (3a, 3b, 3c), …
も明らかにピタゴラス数となる。そのため、ピタゴラス数のリスト化には (a, b, c) の最大公約数が 1 であるもののみを列挙する。これを原始ピタゴラス数(英: primitive Pythagorean triple)という。一般のピタゴラス数 (a, b, c) は、原始ピタゴラス数の各項の数を自然数倍したものとして一意に表される。
ピタゴラス数はディオファントス方程式 a2 + b2 = c2 の整数解であるため、ピタゴラス数は非線形ディオファントス方程式の最も古い既知の解の一つである。
歴史[編集]
ピタゴラス数は古くから知られている。最も古い既知の記録は、紀元前1800年頃のバビロニアの粘土板であるプリンプトン322からのもので、六十進法で書かれている。1900年の初期にエドガージェームズバンクスによって発見され、1922年にジョージアーサープリンプトンに10ドルで売却された[1]。
ピタゴラス数の性質[編集]
ピタゴラス数は、
- a または b は 4 の倍数
- a または b は 3 の倍数
- a または b または c は 5 の倍数
という性質を持つ。 したがって、a と b と c の積は、常に 60 の倍数となる。
生成式[編集]
ピタゴラス数は原始ピタゴラス数の自然数倍として表せる。原始ピタゴラス数の生成式としては、次のユークリッドの式とブラフマグプタによる式が知られている。
ユークリッドの式[2]またはピタゴラスの公式[3]とは、原始ピタゴラス数 (a, b, c) は
- (a, b, c) = (m2 − n2, 2mn, m2 + n2) または (2mn, m2 − n2, m2 + n2)
の形のことである。ここで、m, n は自然数で、
を満たす。
ブラフマグプタの式とは、
- (a, b, c) = (p2 − q2/2, pq, p2 + q2/2) または (pq, p2 − q2/2, p2 + q2/2)
の形のことである。ここで、p, q は自然数で、
- p, q は互いに素
- p > q
- p, q は奇数
を満たす。
したがって、一般のピタゴラス数 (a, b, c) は次のように表せる:
- a = k・(m2 − n2), b = k・2mn, c = k・(m2 + n2)(k は自然数)
脚注[編集]
- ^ Robson, Eleanor (2002), “Words and Pictures: New Light on Plimpton 322”, The American Mathematical Monthly 109 (2): 105-120, doi:10.1080/00029890.2002.11919845
- ^ Joyce, D. E. (1997-06), “Book X, Proposition XXIX”, Euclid's Elements, Clark University
- ^ 細矢治夫『三角形の七不思議』2013/07/20、p.62
