量子化誤差
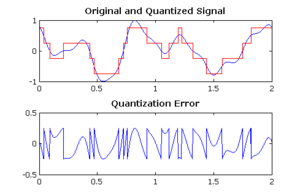
量子化誤差(りょうしかごさ、Quantization Error)または量子化歪み(りょうしかひずみ、Quantization Distortion)とは、信号をアナログからデジタルに変換する際に生じる誤差である。
概要[編集]
アナログ信号からデジタル信号への変換(デジタイズ)は、信号の細部を無視する変換であるため、元の信号からの誤差が必ず発生する。このような誤差を、量子化誤差と呼び、発生する雑音は、量子化雑音(Quantization Noise)と呼ばれる。
量子化誤差の大きさは、量子化の解像度やアナログ-デジタル変換回路のビット数に依存する。
量子化誤差モデル[編集]
さまざまな物理量が実際に物理的な実体によって量子化される。これが当てはまる分野の例としては、電子工学(電子による量子化)、光学(光子による量子化)、化学(分子による量子化)などである。これをその系の「量子化雑音限界」と呼ぶこともある。これは、「量子化誤差」の別の現れでもあり、この場合は理論的モデルはアナログでも、実際の現象はデジタル的になっているのである。量子限界付近では、アナログとデジタルの区別はなくなる。
量子化雑音モデル[編集]
量子化雑音(りょうしかざつおん、英: Quantization noise)は、電気通信やデジタル信号処理におけるアナログ-デジタル変換過程での量子化で生まれるノイズである。これはアナログ値とデジタル値の量子化誤差によって生じる。このノイズは非線形で元の信号に依存したものとなる。量子化雑音はいくつかの方法でモデル化される。
量子化雑音を以下のように二乗平均平方根誤差として表現できる。
ここで は変換回路に入力されるアナログ電圧範囲(ボルト)、 は変換回路の量子化ビット数、は標本化周期(秒)、 は変換回路の負荷抵抗(オーム)である。
理想的なアナログ-デジタル変換回路では、S/N比は以下のように求められる。
16ビットオーディオでのダイナミックレンジは 6.02 · 16 = 96.3 dB である。
この値は、理想的なアナログ-デジタル変換では量子化誤差が −1/2 LSB から +1/2 LSB まで一様に分布すると仮定したものである。また、信号の値が量子化可能な範囲に全て含まれていると仮定している。量子化可能な範囲を調べるには三角波やのこぎり波を最大強度で入力してみればよい。
入力信号が最大強度の正弦波の場合、信号の値の確率分布は一様ではなくなり、以下のような式でS/N比が求められる。
ここでも量子化誤差の分布は一様であると仮定している。高解像度のアナログ-デジタル変換回路はこの式に近い特性を示すが、4ビットまでの低解像度の変換回路では、入力信号が量子化可能範囲を超えてしまう問題が強くなり、この式とはかけ離れてしまう。







