等角航路
等角航路(とうかくこうろ)とは、地球上の2点間を結ぶ航路のうち、進行方向が経線となす角度が常に一定となるものをいう。航程線とも呼ばれる。
概要[編集]
地球上の2点を航路で結ぶことを考えた場合、地形や海流などの外的要因がなければ、最短距離を結ぶ大圏航路が、燃料や所要時間を節約する上で最も望ましい。
大圏航路を進むには、現在位置に応じて常に進行方向の方位を修正する必要がある。GPSなどの方法で正確な現在位置を知ることのできる現代では、大圏航路を利用することに問題は少ない。
しかしそのような物のなかった時代に、沿岸を離れて目印のない大洋を渡る航路を進むには、大圏航路は非常に困難であった。天体観測によって緯度を測定することはできても、経度を測定することはできなかったためである。
これに対し等角航路は、現在どの地点まで進んでいるかを考慮する必要がなく、常に一定の方位を維持すればよい。羅針盤により方位は容易にわかるため、大航海時代に広く利用された。
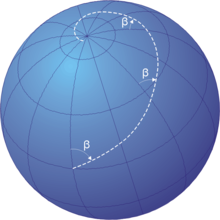
同じ発想であり、球面上の等角スパイラルと考えて求める事が出来る。等角航路上の点(緯度, 経度)が、定点である極 P の方向に対して常に角βをとる時、βが90度の倍数の時は緯線または経線である。βが90度の倍数でない時、 とすると、微小変化は
- つまり
この式はメルカトル図法における赤道と緯線の間の距離を求める式と定数倍の違いだけであり、赤道との交点を である。( はグーデルマン関数。)
地図と等角航路[編集]
地図の投影法のうち、任意の地点で角度が保存される図法を正角図法と呼ぶ。メルカトル図法はその代表的な例である。
正軸法のメルカトル図法の地図上では任意の二点間の等角航路が直線で表されるため、海図として広く使用されてきた。
メルカトル図法で描かれた世界地図を目にすることは多い。この地図上では、等角航路が直線となるのに対し、大圏航路は極地に近づくように湾曲した曲線として描かれる。
たとえば、東京からサンフランシスコへ向かう場合、緯度はほぼ等しい(東京が北緯35度41分、サンフランシスコが北緯37度46分)ので、等角航路は緯線に沿ってほぼ東に向かう直線となる。これに対し大圏航路は、地図上では東京から北東に向かい、次第に東に向きを変えながら北緯50度近辺、アリューシャン諸島まで北上し、その後は南東へと向きを変える曲線となる。
しかしこの2つのコースを地球儀上に移し替えてみると、大圏航路がほぼ直線的な最短コースであるのに対し、等角航路が実際には南に湾曲した曲線であることがわかる。
航路を結ぶ2点が同じ経度にあり南北方向に進む場合、あるいは2点が共に赤道上で東西方向に進む場合のみ、等角航路は大圏航路と重なり最短距離となる。
メルカトル図法の他に、図法の中心点からの等角航路が正しく示される図法として 航程方位図法 が1935年に考案された。等角航路が直線になるのは図法の中心点からのみではあるものの、等角航路の長さも正しく、地球全体を表示しても有限で収まる。
関連項目[編集]
脚注[編集]







