原子価殻電子対反発則

原子価殻電子対反発則(げんしかかくでんしついはんぱつそく、英: valence shell electron pair repulsion rule)は、化学において用いられる、分子の構造を簡単に予測するための模型(モデル)である[1]。電子対反発理論やVSEPR理論と呼ばれる場合もある。この理論においては、原子を取り囲む価電子対が互いに反発する傾向にあり、ゆえにこの反発を最小化する配置を取ると仮定し、これによって分子の幾何構造を予測する。
「VSEPR」は、英語では"ves-pur"[2]:410あるいは "vuh-seh-per."[3]と発音されている。この理論の開発者に因んでナイホルム・ギレスピー理論と呼ばれることもある。
歴史[編集]
分子の幾何構造と価電子の数(共有および非共有)との間の相関関係の着想は1939年に槌田龍太郎によって最初に提唱され[4]、それとは独立に1940年にオックスフォード大学のネビル・シジウィック とハーバート・パウエルによってベーカー講義で述べられた[5]。1957年、ユニヴァーシティ・カレッジ・ロンドンのロナルド・ギレスピーとロナルド・シドニー・ナイホルムがこの概念をより詳細な理論へと洗練させ、様々な代替構造間からの選択を可能にした[6][7]。
近年、VSEPR理論は科学的正確性と教育上の価値の両方の視点から時代遅れのモデルとして批判されてきた[8]。具体的には、VSEPR理論における水およびカルボニル化合物の等価な孤立電子対は、分子オービタルと自然結合オービタルの対称性(σ vs. π)における根本的な相違を無視している。この違いは化学的に重要なことがある。そのうえ、孤立電子対が結合性電子対「よりも大きい」ことを示唆する計算的または実験的証拠はほとんど存在しない。分子構造を説明するための単純なモデルとしてベント則がVSEPR理論を置き換えることができると提案されている。にもかかわらず、VSEPR理論は単純な分子の構造と電子分布の本質的要素の多くを捕えており、ほとんどの学部の一般化学の講義で教えられ続けている。
概要[編集]
VSEPR理論は、分子中の非水素原子の周りの電子対の配置を予測するために用いられる。特に、単純で対称性を持つ分子が対象となる。
中心原子の原子価殻中の電子対の数は分子のルイス構造を描き、全ての結合基と非共有電子対を示した後に決定される[2]:410–417。VSEPR理論では、二重結合または三重結合は単一の結合基として扱われる[2]。中心原子に結合した原子の数とその非結合性価電子によって作られる非共有電子対の数の和は中心原子の立体数と呼ばれる。
電子対(または多重結合の場合は基)は中心原子を中心とした球の表面上にあり、それらの間の距離を最大化することによって相互反発を最小化する位置を占める傾向にあると仮定される[2]:410–417[9]。電子対(または基)の数は、したがって、それらが取る全体の構造を決定する。例えば、中心原子を取り囲む2つの電子対が存在する時、相互反発はそれらが球の反対側の極にある時に最小となる。したがって、中心原子は「直線」構造を取ると予測される。中心原子を取り囲む3つの電子対が存在するならば、それらの反発は中心原子を中心とする正三角形の各頂点にそれらを置くことによって最小化される。したがって、予測構造は「三角形」である。同様にして、4電子対では、最適配置は「四面体」である[2]:410–417。
反発の度合い[編集]
全体構造は、「結合」電子対と「非結合」電子対との間を区別することによってさらに精緻化される。結合電子対は隣合う原子との間のσ結合で共有されている。隣りの原子と非結合(非共有)電子対とを比べると、正の電荷を持つ原子核の近くに保持されている非結合電子対よりも隣りの原子の方が中心原子から遠くに位置している。VSEPR理論はしたがって非共有電子対による反発の方が結合電子対による反発よりも大きいと見る。そのようなものとして、分子が反発の程度が異なる2つの相互作用を持つ時、VSEPR理論は非共有電子対がより反発を受けないような位置を占める構造を予測する。非共有電子対–非共有電子対(lp–lp)反発は非共有電子対–結合電子対(lp–bp)反発よりも強いと見なされ、非共有電子対–結合電子対反発は結合電子対–結合電子対反発よりも強いと見なされる。この違いが、2つ以上の非等価な位置が可能な時に全体構造を決定する助けとなる[2]:410–417。例えば、5つの価電子対が中心原子を取り囲んでいる時、それらは2つが共線的「アキシアル」(軸方向)位、3つが「エクアトリアル」(赤道方向)位にある三方両錐形分子構造を取る。アキシアル位の電子対からは90° しか離れていない位置に3つのエクアトリアル位電子対と180° 離れた位置に逆側のアキシアル位電子対がある。それに対して、エクアトリアル位電子対は90° の位置には2つだけ、120° の位置に2つの電子対を持つ。アキシアル位はエクアトリアル位よりも反発を受けるため、90° と近くにある電子対からの反発がより重要である。したがって、非共有電子対が存在する時、それらは次節の図で示されているように立体数が5の時のエクアトリアル位を占める傾向にある[9]。
非共有電子対と結合電子対との間の違いは、理想的な構造からのずれを合理的に説明するためにも使うことができる。例えば、H2O分子はその原子価殻に4つの電子対(2つの非共有電子対および2つの結合電子対)を持つ。4つの電子対は四面体の頂点を大雑把に指すように広がる。しかしながら、2つのO–H結合間の結合角は正四面体の109.5° ではなくわずか104.5° である。これは、2つの非共有電子対(それらの電子対は酸素原子核に近い位置にある)が2つの結合対よりも大きな相互反発を及ぼすためである[2]:410–417[9]。
上級の説明では、上述した差異を2つの規則で置き換える。
- ベント則: より電気的陽性の配位子の電子対より大きな反発を生む。これは、なぜPClF4中のClがエクアトリアル位を好み、なぜ二フッ化酸素の結合角(103.8°)が水のもの(104.5°)よりも小さいかを説明する。非共有電子対は、電気的陽性の極限にある「虚配位子」によって規則が守られている、この規則の特殊な場合と考えられる。
- より高い結合次数はより大きな反発を生む 。これは、なぜホスゲンにおいて、塩素は酸素よりも電気的に陽性であるにもかかわらず、酸素–塩素結合角(124.1°)が塩素–塩素結合角(111.8°)よりも大きいかを説明する。炭酸イオンでは、共鳴のため3つの結合角全てが等価である。
AXE法[編集]
電子を数える「AXE法」がVSEPR理論を適用する時に一般的に用いられる。Aは中心原子を表わし、暗黙の下付き文字1を常に持つ。Xは個々の配位子(Aに結合した原子)を表わす。E は中心原子を取り囲む孤立電子「対」の数を表わす[2]:410–417。XとEの和は立体数と呼ばれる。
立体数とXおよびEの分布に基づいて、VSEPR理論は以下の表を予測する。幾何配置は電子配置ではなく原子の位置のみにしたがって命名されていることに留意すべきである。
| 分子構造 | 分子形 | 電子配置 (黄色は非共有電子対) |
分子の形状 | 結合角 | 例 |
|---|---|---|---|---|---|
| AX1En | 二原子分子 | HF、O2 | |||
| AX2E0 | 直線形 | BeCl2 | |||
| AX2E3 |  |
XeF2、I3- | |||
| AX2E1 | 折れ線形 |  |
 |
NO2−、SO2、O3 | |
| AX2E2 | 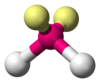 |
 |
H2O、OF2 | ||
| AX3E0 | 平面三角形 |  |
 |
BCl3 | |
| AX3E1 | 三角錐形 |  |
 |
NH3 | |
| AX3E2 | T字形 |  |
 |
ClF3 | |
| AX4E0 | 四面体形 | 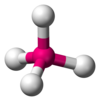 |
 |
CH4 | |
| AX4E1 | シーソー形 |  |
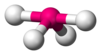 |
SF4 | |
| AX4E2 | 平面四角形 |  |
 |
XeF4 | |
| AX5E0 | 三方両錐形 |  |
 |
PCl5 | |
| AX5E1 | 四角錐形 | 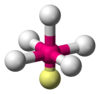 |
 |
ClF5、BrF5 | |
| AX5E2 | 平面五角形 |  |
 |
XeF5- | |
| AX6E0 | 八面体形 | 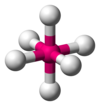 |
 |
SF6 | |
| AX6E1 | 五角錐形 |  |
 |
XeF6 | |
| AX7E0 | 五方両錐形 |  |
 |
IF7 |
出典[編集]
- ^ Jolly, W. L. (1984). Modern Inorganic Chemistry. McGraw-Hill. p. 77–90. ISBN 0-07-032760-2
- ^ a b c d e f g h Petrucci, R. H.; W. S., Harwood; F. G., Herring (2002). General Chemistry: Principles and Modern Applications (8th ed.). Prentice-Hall. ISBN 0-13-014329-4
- ^ Stoker, H. Stephen (2009). General, Organic, and Biological Chemistry. Cengage Learning. p. 119. ISBN 978-0-547-15281-3
- ^ 槌田 龍太郎 (1939). “新簡易原子價論”. 日本化學會誌 60 (3): 245–256. doi:10.1246/nikkashi1921.60.245.
- ^ Sidgwick, N. V.; Powell, H. M. (1940). “Bakerian Lecture. Stereochemical Types and Valency Groups”. Proc. Roy. Soc. A 176: 153–180. doi:10.1098/rspa.1940.0084.
- ^ Gillespie, R. J.; Nyholm, R. S. (1957). “Inorganic stereochemistry”. Quart. Rev. Chem. Soc. 11: 339. doi:10.1039/QR9571100339.
- ^ Gillespie, R. J. (1970). “The electron-pair repulsion model for molecular geometry”. J. Chem. Educ. 47 (1): 18. doi:10.1021/ed047p18.
- ^ Clauss, Allen D.; Nelsen, Stephen F.; Ayoub, Mohamed; Moore, John W.; Landis, Clark R.; Weinhold, Frank (2014-10-08). “Rabbit-ears hybrids, VSEPR sterics, and other orbital anachronisms” (英語). Chem. Educ. Res. Pract. 15 (4): 417–434. doi:10.1039/c4rp00057a. ISSN 1756-1108.
- ^ a b c Miessler, G. L.; Tarr, D. A. (1999). Inorganic Chemistry (2nd ed.). Prentice-Hall. p. 54–62. ISBN 0-13-841891-8
