第二基本形式

微分幾何学における第二基本形式（英: second fundamental form）または形テンソル（shape tensor）とは、3次元ユークリッド空間の滑らかな曲面（smooth surface）の接平面上の2次形式を言う。普通、 $\mathrm {I\!I}$ と表記される（「２」と読む）。第一基本形式とともに、曲面の外在的不変量、例えば曲面の主曲率、を定義するのに役立つ。より一般的には、このような2次形式は、リーマン多様体に滑らかに埋め込まれた部分多様体に対して定義される。

^R3の曲面

第二基本形式の定義

動機

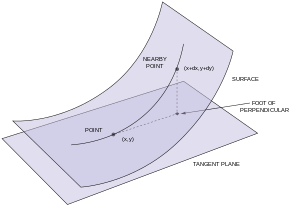
R³の媒介変数表示された曲面 S の第二基本形式は、ガウスによって導入され、研究された。まず、曲面が表面が2回連続的微分可能（continuously differentiable）な関数 z = f(x,y) のグラフであり、平面 z = 0 が原点で曲面に接していると仮定する。そして、 f とそれの x および y に関する偏導関数は、（0,0）でゼロになるとする。それ故、（0,0）での f のテイラー展開は次のように2次の項で始まることになる。

$z=L{\frac {x^{2}}{2}}+Mxy+N{\frac {y^{2}}{2}}+{\text{higher order terms}}\,,$

座標 (x,y) で表される原点における第二基本形式は2次形式となる。

$L\,dx^{2}+2M\,dx\,dy+N\,dy^{2}\,.$

S 上の滑らかな点 P に対し、平面 z = 0 が P で S に接するように座標系を選択し、同様の方法で第二基本形式を定義できる。

古典的な記法

一般的な媒介変数表示された曲面の第二基本形式は、次のように定義される。 r = r(u,v) を R³ の曲面の正則（regular）な媒介変数表示とする。ここで、 r は２変数の滑らかなベクトル値関数である。u と v に関する r の偏導関数は r_u と r_v で表示するのが普通である。媒介変数表示の正則性（regularity）は、r の定義域において 任意の(u,v) に対して r_u と r_v が線型独立であることを意味する。すなわち、r_u と r_v は、各点で S の接平面を張る（span）ことになる。同様に、外積 r_u × r_v は曲面に垂直な非ゼロのベクトルとなる。媒介変数表示は、したがって、単位法線ベクトル n の場を次のように定義する。

$\mathbf {n} ={\frac {\mathbf {r} _{u}\times \mathbf {r} _{v}}{|\mathbf {r} _{u}\times \mathbf {r} _{v}|}}\,.$

第二基本形式はたいてい次のように書かれる。

$\mathrm {I\!I} =L\,du^{2}+2M\,du\,dv+N\,dv^{2}\,,$

接平面の基底 {r_u, r_v} の行列は次のようになる。

${\begin{bmatrix}L&M\\M&N\end{bmatrix}}\,.$

媒介変数表示による uv 平面における与えられた点での係数 L, M, N は、その点での r の2次偏導関数を、S の法線上に射影することによって与えられ、内積を使用して次のように計算できる。

$L=\mathbf {r} _{uu}\cdot \mathbf {n} \,,\quad M=\mathbf {r} _{uv}\cdot \mathbf {n} \,,\quad N=\mathbf {r} _{vv}\cdot \mathbf {n} \,.$

ヘッセ行列 H の符号付き距離場（signed distance field）に対して、第二基本形式の係数は次のように計算される。

$L=-\mathbf {r} _{u}\cdot \mathbf {H} \cdot \mathbf {r} _{u}\,,\quad M=-\mathbf {r} _{u}\cdot \mathbf {H} \cdot \mathbf {r} _{v}\,,\quad N=-\mathbf {r} _{v}\cdot \mathbf {H} \cdot \mathbf {r} _{v}\,.$

物理学における記法

一般的な媒介変数表示された曲面 S の第二基本形式は、次のように定義される。

r = r(u¹,u²) を R³ の曲面の正則な媒介変数表示とする。ここで、r は２変数の滑らかなベクトル値関数である。r の u^α に関する偏導関数を r_α （α = 1, 2）と表示するのが普通である。媒介変数表示の正則性（regularity）は、r₁ と r₂ が r の定義域内の任意の (u¹,u²) に対して線形独立であることを意味する。したがって、r₁ と r₂ が各点で S の接平面を張る（span）ことを意味する。同様に、外積 r₁ × r₂ は曲面に垂直な非ゼロのベクトルとなる。媒介変数表示は、したがって、単位法線ベクトル n の場を次のように定義する。

$\mathbf {n} ={\frac {\mathbf {r} _{1}\times \mathbf {r} _{2}}{|\mathbf {r} _{1}\times \mathbf {r} _{2}|}}\,.$

第二基本形式は大抵次のように書かれる。

$\mathrm {I\!I} =b_{\alpha \beta }\,du^{\alpha }\,du^{\beta }\,.$

上記の式は、アインシュタインの縮約記法を用いている。

媒介変数表示された u¹u² 平面における与えられた点における第二基本形式の係数 b_αβ は、その点での r の2次偏導関数を、S の法線に射影することで与えられる。そして、法線ベクトル n を用いて次のように計算できる。

$b_{\alpha \beta }=r_{\,\alpha \beta }^{\ \ \,\gamma }n_{\gamma }\,.$

リーマン多様体の超曲面

ユークリッド空間において、第二基本形式は次のように与えられる。

$\mathrm {I\!I} (v,w)=-\langle d\nu (v),w\rangle \nu$

ここで、 ν はガウス写像であり、 dν はベクトル値の微分形式と見なされる ν の微分であり、括弧はユークリッド空間の計量テンソルを表示している。

より一般的には、リーマン多様体では、第二基本形式は、超曲面の Sで示される形作用素（shape operator）を記述するための同等の方法である。

$\mathrm {I} \!\mathrm {I} (v,w)=\langle S(v),w\rangle n=-\langle \nabla _{v}n,w\rangle n=\langle n,\nabla _{v}w\rangle n\,,$

ここで、∇_vw は全体多様体（ambient manifold）の共変微分、n は超曲面上の法線ベクトル場を表示している。（アフィン接続に捩じれがない場合、第二基本形式は対称となる。 ）

第二基本形式の符号は、 n の方向の選択に依存する（これは超曲面の共方向（co-orientation）と呼ばれる。ユークリッド空間の曲面の場合、これは同様に曲面の向きの選択によって与えられる。）

任意の余次元への一般化

第二基本形式は、任意の余次元（codimension）に一般化できる。その場合、それは法ベクトル束（normal bundle）における値を持つ接空間上の二次形式である。次のように定義できる。

$\mathrm {I\!I} (v,w)=(\nabla _{v}w)^{\bot }\,,$

ここで、$(\nabla _{v}w)^{\bot }$ は共変微分 $\nabla _{v}w$ の法ベクトル束への直交射影（orthogonal projection）を表す。

ユークリッド空間では、部分多様体の曲率テンソルは次の式で表すことができる。

$\langle R(u,v)w,z\rangle =\langle \mathrm {I} \!\mathrm {I} (u,z),\mathrm {I} \!\mathrm {I} (v,w)\rangle -\langle \mathrm {I} \!\mathrm {I} (u,w),\mathrm {I} \!\mathrm {I} (v,z)\rangle .$

これは、ガウスの驚異の定理の一般化と見なすことができるため、ガウス方程式と呼ばれる。

一般的なリーマン多様体の場合、全体空間（ambient space）の曲率を追加する必要がある。N がリーマン多様体 (M,g) に埋め込まれた多様体である場合、 (M,g) から誘導された計量を持つ N の曲率テンソル R_N は、第二基本形式と M の曲率テンソル R_M を用いて次のように表現することができる。

$\langle R_{N}(u,v)w,z\rangle =\langle R_{M}(u,v)w,z\rangle +\langle \mathrm {I} \!\mathrm {I} (u,z),\mathrm {I} \!\mathrm {I} (v,w)\rangle -\langle \mathrm {I} \!\mathrm {I} (u,w),\mathrm {I} \!\mathrm {I} (v,z)\rangle \,.$

関連項目

• 第一基本形式
• ガウス曲率
• ガウス・コダッチ方程式
• 形作用素
• 第三基本形式
• トートロジー形式

参考文献

• Guggenheimer, Heinrich (1977). “Chapter 10. Surfaces”. Differential Geometry. Dover. ISBN 0-486-63433-7 
• Kobayashi, Shoshichi; Nomizu, Katsumi (1996). Foundations of Differential Geometry, Vol. 2 (New ed.). Wiley-Interscience. ISBN 0-471-15732-5 
• Spivak, Michael (1999). A Comprehensive introduction to differential geometry (Volume 3). Publish or Perish. ISBN 0-914098-72-1 

外部リンク

• Steven Verpoort (2008) Geometry of the Second Fundamental Form: Curvature Properties and Variational Aspects from Katholieke Universiteit Leuven.