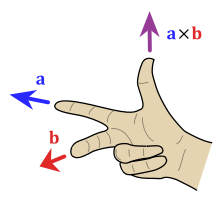
3次元ベクトル a b a × b a b 平行四辺形 の面積 に等しい大きさを持ち、平行四辺形に垂直 なベクトルとなる。 クロス積 ( クロスせき 、( 英 : cross product )は、3次元 空間(3次元有向 内積空間 )において定義される、2つのベクトル から新たなベクトルを与える二項演算 である。
2つのベクトル a , b のクロス積は乗算記号 を用いて a × b 角括弧 を用いて [a , b ] と表される。
「クロス積」という呼称は、積の記号に十字(× )を用いることに由来する(同様にベクトルの内積 は点(⋅ )を用いることからドット積 と呼ばれる)。またクロス積の別称として、ベクトル積 ( ベクトルせき 、( 英 : vector product )がある。「ベクトル積」は積 a × b a ⋅ b
日本語 や中国語 では、クロス積(叉積 、叉积 )をしばしば外積 (外積 、外积 )と呼び、しばしば同義語として扱う。しかし「外積」という語は、より一般には外積代数 における楔積も指し、必ずしも「クロス積」とは一致しない。
楔積とクロス積を区別のため、前者を外積と呼び後者をクロス積と呼ぶ。
outer product もまた「外積」と訳されるが、こちらは直積 (direct product )を意味する。
2つのベクトル a b
乗算記号 を用いる場合:
a
×
b
{\displaystyle {\boldsymbol {a}}\times {\boldsymbol {b}}}
角括弧 を用いる場合:
[
a
,
b
]
{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]}
右手の法則 によるクロス積の向き右手系 の外積3次元空間上の2つのベクトル a b a b
a
×
b
=
|
a
|
|
b
|
sin
(
θ
)
n
{\displaystyle {\boldsymbol {a}}\times {\boldsymbol {b}}=\left|{\boldsymbol {a}}\right|\left|{\boldsymbol {b}}\right|\sin(\theta )\ {\boldsymbol {n}}}
ただし、θ は2つのベクトルのなす角の角度、|⋅| はベクトルの大きさ 、n 垂直 な単位ベクトル を表す(n 右手系 になるように取る)。
行列式による定義 [ 編集 ] 3次元の向き付けられたベクトル空間におけるクロス積は、任意のベクトル v ドット積 との間に
v
⋅
(
a
×
b
)
=
det
⟨
v
,
a
,
b
⟩
{\displaystyle {\boldsymbol {v}}\cdot ({\boldsymbol {a}}\times {\boldsymbol {b}})=\det \langle {\boldsymbol {v}},{\boldsymbol {a}},{\boldsymbol {b}}\rangle }
の関係を満たすベクトルの二項演算である。ここで ⟨ · , · , · ⟩ はベクトルを標準的な基底により列ベクトル と同一視することで得られる3次正方行列 である。det は行列式 を表す。
幾何的なベクトルの演算として定義できる。
行列式の交代性から、
a
⋅
(
a
×
b
)
=
b
⋅
(
a
×
b
)
=
0
{\displaystyle {\boldsymbol {a}}\cdot ({\boldsymbol {a}}\times {\boldsymbol {b}})={\boldsymbol {b}}\cdot ({\boldsymbol {a}}\times {\boldsymbol {b}})=0}
である。
従って、2つのベクトル a b a b a b 平面 の法線 と平行な方向を向いている。
ただし、法線のどちらの方向に向いているかは座標軸の選び方に依存し、右手系 と左手系 に分けられる。右手系の場合は、a b a b a b b a
行列式とスカラー積の線型性からクロス積も双線型性をもつ。 特に、2つのベクトル a b a b a b a b θ とすれば、標準的な基底の下で
a
=
(
a
0
0
)
,
b
=
(
b
cos
θ
b
sin
θ
0
)
{\displaystyle {\boldsymbol {a}}={\begin{pmatrix}a\\0\\0\\\end{pmatrix}},~{\boldsymbol {b}}={\begin{pmatrix}b\cos \theta \\b\sin \theta \\0\\\end{pmatrix}}}
と成分表示することができる。これらのクロス積は
a
×
b
=
(
0
0
a
b
sin
θ
)
{\displaystyle {\boldsymbol {a}}\times {\boldsymbol {b}}={\begin{pmatrix}0\\0\\ab\sin \theta \\\end{pmatrix}}}
となる。従ってクロス積の大きさは
|
a
×
b
|
=
|
a
|
|
b
|
sin
θ
{\displaystyle \vert {\boldsymbol {a}}\times {\boldsymbol {b}}\vert =\vert {\boldsymbol {a}}\vert \,\vert {\boldsymbol {b}}\vert \sin \theta }
であり、2つのベクトルが作る平行四辺形 の面積に等しい。
成分表示 [ 編集 ] 標準的な基底を (e i e j δi,j として、ベクトル a ai =(e i a
a
≐
(
a
1
a
2
a
3
)
{\displaystyle {\boldsymbol {a}}\doteq {\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\\\end{pmatrix}}}
を行う。ベクトル a b a b
[
a
,
b
]
1
=
(
e
1
,
[
a
,
b
]
)
=
|
1
a
1
b
1
0
a
2
b
2
0
a
3
b
3
|
=
a
2
b
3
−
a
3
b
2
{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]_{1}=({\boldsymbol {e}}_{1},[{\boldsymbol {a}},{\boldsymbol {b}}])={\begin{vmatrix}1&a_{1}&b_{1}\\0&a_{2}&b_{2}\\0&a_{3}&b_{3}\\\end{vmatrix}}=a_{2}b_{3}-a_{3}b_{2}}
[
a
,
b
]
2
=
(
e
2
,
[
a
,
b
]
)
=
|
0
a
1
b
1
1
a
2
b
2
0
a
3
b
3
|
=
a
3
b
1
−
a
1
b
3
{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]_{2}=({\boldsymbol {e}}_{2},[{\boldsymbol {a}},{\boldsymbol {b}}])={\begin{vmatrix}0&a_{1}&b_{1}\\1&a_{2}&b_{2}\\0&a_{3}&b_{3}\\\end{vmatrix}}=a_{3}b_{1}-a_{1}b_{3}}
[
a
,
b
]
3
=
(
e
3
,
[
a
,
b
]
)
=
|
0
a
1
b
1
0
a
2
b
2
1
a
3
b
3
|
=
a
1
b
2
−
a
2
b
1
{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]_{3}=({\boldsymbol {e}}_{3},[{\boldsymbol {a}},{\boldsymbol {b}}])={\begin{vmatrix}0&a_{1}&b_{1}\\0&a_{2}&b_{2}\\1&a_{3}&b_{3}\\\end{vmatrix}}=a_{1}b_{2}-a_{2}b_{1}}
あるいは
[
a
,
b
]
≐
(
a
2
b
3
−
a
3
b
2
a
3
b
1
−
a
1
b
3
a
1
b
2
−
a
2
b
1
)
{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]\doteq {\begin{pmatrix}a_{2}b_{3}-a_{3}b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2}-a_{2}b_{1}\\\end{pmatrix}}}
となる。以上のことを形式的に
[
a
,
b
]
=
|
e
1
a
1
b
1
e
2
a
2
b
2
e
3
a
3
b
3
|
{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]={\begin{vmatrix}{\boldsymbol {e}}_{1}&a_{1}&b_{1}\\{\boldsymbol {e}}_{2}&a_{2}&b_{2}\\{\boldsymbol {e}}_{3}&a_{3}&b_{3}\end{vmatrix}}}
と表現することもある。
エディントンのイプシロン εijk を用いると
[
a
,
b
]
i
=
∑
j
,
k
ϵ
i
j
k
a
j
b
k
{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]_{i}=\sum _{j,k}\epsilon _{ijk}a_{j}b_{k}}
である。
クロス積の幾何的意味 [ 編集 ] (図1)2つのベクトルのクロス積の大きさは、それらが作る平行四辺形 の大きさとなる。 (図2)3つのベクトルのクロス積は、平行六面体 を定義する。 2つのベクトルのクロス積は、2つのベクトルが作る平行四辺形 の大きさに等しい(図1)。
‖
a
×
b
‖
=
‖
a
‖
‖
b
‖
|
sin
θ
|
{\displaystyle \left\|{\boldsymbol {a}}\times {\boldsymbol {b}}\right\|=\left\|{\boldsymbol {a}}\right\|\left\|{\boldsymbol {b}}\right\|\left|\sin \theta \right|}
また、3つのベクトル a b c 平行六面体 を定義する。(図2)。この平行六面体 の体積 V について、
V
=
|
a
⋅
(
b
×
c
)
|
{\displaystyle V=|{\boldsymbol {a}}\cdot ({\boldsymbol {b}}\times {\boldsymbol {c}})|}
が成り立つ。ここで絶対値記号を付けたのは、3つのベクトルのクロス積が負になる場合を考慮してのことである。
なお、
a
⋅
(
b
×
c
)
=
b
⋅
(
c
×
a
)
=
c
⋅
(
a
×
b
)
{\displaystyle {\boldsymbol {a}}\cdot ({\boldsymbol {b}}\times {\boldsymbol {c}})={\boldsymbol {b}}\cdot ({\boldsymbol {c}}\times {\boldsymbol {a}})={\boldsymbol {c}}\cdot ({\boldsymbol {a}}\times {\boldsymbol {b}})}
である。
分配律 [ 編集 ] 一般に分配律
a × (b + c ) = a × b + a × c [a , b+c ] = [a , b ] + [a , c ] )が成り立つ。
反交換律 [ 編集 ] 一般に反交換律
a × b = − b × a [b , a ] = -[a , b ] )
が成り立つ。これは、行列式 の交代性やリー代数 の反交換性 からも説明できる。特に、自分自身とのベクトル積は
[
a
,
a
]
=
0
{\displaystyle [{\boldsymbol {a}},{\boldsymbol {a}}]={\boldsymbol {0}}}
であり恒等的に零ベクトルである。(複零性)
内積の性質、
(
b
,
a
)
=
(
a
,
b
)
{\displaystyle ({\boldsymbol {b}},{\boldsymbol {a}})=({\boldsymbol {a}},{\boldsymbol {b}})}
(
a
,
a
)
=
|
a
|
2
{\displaystyle ({\boldsymbol {a}},{\boldsymbol {a}})=|{\boldsymbol {a}}|^{2}}
と異なることに注意が必要。
双線型性 [ 編集 ] 行列式の多重線型性 から、ベクトル積も双線型性 である。任意のベクトルに a b c k 、l に対して
[
a
,
k
b
+
l
c
]
=
k
[
a
,
b
]
+
l
[
a
,
c
]
{\displaystyle [{\boldsymbol {a}},k{\boldsymbol {b}}+l{\boldsymbol {c}}]=k[{\boldsymbol {a}},{\boldsymbol {b}}]+l[{\boldsymbol {a}},{\boldsymbol {c}}]}
[
k
b
+
l
c
,
a
]
=
k
[
b
,
a
]
+
l
[
c
,
a
]
{\displaystyle [k{\boldsymbol {b}}+l{\boldsymbol {c}},{\boldsymbol {a}}]=k[{\boldsymbol {b}},{\boldsymbol {a}}]+l[{\boldsymbol {c}},{\boldsymbol {a}}]}
が成り立つ。特に k =l =0 であれば
[
a
,
0
]
=
[
0
,
a
]
=
0
{\displaystyle [{\boldsymbol {a}},{\boldsymbol {0}}]=[{\boldsymbol {0}},{\boldsymbol {a}}]={\boldsymbol {0}}}
である。内積(スカラー積)の場合は零ベクトル との積はスカラーのゼロであるが、ベクトル積の場合は零ベクトルであることに注意が必要。
ヤコビ恒等式 [ 編集 ] ベクトル積による演算結果はベクトルなので、別のベクトルとのベクトル積を考えることができる。3つのベクトルのベクトル積はベクトル三重積 と呼ばれている。ベクトル三重積は
[
a
,
[
b
,
c
]
]
=
(
a
,
c
)
b
−
(
a
,
b
)
c
{\displaystyle [{\boldsymbol {a}},[{\boldsymbol {b}},{\boldsymbol {c}}]]=({\boldsymbol {a}},{\boldsymbol {c}})\,{\boldsymbol {b}}-({\boldsymbol {a}},{\boldsymbol {b}})\,{\boldsymbol {c}}}
となる。3つのスカラーの積と異なり、ベクトル三重積では一般に
[
a
,
[
b
,
c
]
]
−
[
[
a
,
b
]
,
c
]
≠
0
{\displaystyle [{\boldsymbol {a}},[{\boldsymbol {b}},{\boldsymbol {c}}]]-[[{\boldsymbol {a}},{\boldsymbol {b}}],{\boldsymbol {c}}]\neq {\boldsymbol {0}}}
であり、結合法則 が成り立たない。ベクトル積では結合法則に代わって
[
a
,
[
b
,
c
]
]
−
[
[
a
,
b
]
,
c
]
=
[
b
,
[
a
,
c
]
]
{\displaystyle [{\boldsymbol {a}},[{\boldsymbol {b}},{\boldsymbol {c}}]]-[[{\boldsymbol {a}},{\boldsymbol {b}}],{\boldsymbol {c}}]=[{\boldsymbol {b}},[{\boldsymbol {a}},{\boldsymbol {c}}]]}
の関係式が成り立つ。これを変形すれば
[
a
,
[
b
,
c
]
]
+
[
b
,
[
c
,
a
]
]
+
[
c
,
[
a
,
b
]
]
=
0
{\displaystyle [{\boldsymbol {a}},[{\boldsymbol {b}},{\boldsymbol {c}}]]+[{\boldsymbol {b}},[{\boldsymbol {c}},{\boldsymbol {a}}]]+[{\boldsymbol {c}},[{\boldsymbol {a}},{\boldsymbol {b}}]]={\boldsymbol {0}}}
が得られ、ヤコビ恒等式 と呼ばれている。
三重積の証明 [ 編集 ] ベクトル三重積:
a
×
(
b
×
c
)
{\displaystyle {\boldsymbol {a}}\times ({\boldsymbol {b}}\times {\boldsymbol {c}})}
ベクトル
a
{\displaystyle {\boldsymbol {a}}}
(
b
×
c
)
{\displaystyle ({\boldsymbol {b}}\times {\boldsymbol {c}})}
x 成分は
{
a
×
(
b
×
c
)
}
x
=
a
y
(
b
×
c
)
z
−
a
z
(
b
×
c
)
y
=
a
y
(
b
x
c
y
−
b
y
c
x
)
−
a
z
(
b
z
c
x
−
b
x
c
z
)
=
a
y
b
x
c
y
−
a
y
b
y
c
x
−
a
z
b
z
c
x
+
a
z
b
x
c
z
=
(
a
y
c
y
+
a
z
c
z
)
b
x
−
(
a
y
b
y
+
a
z
b
z
)
c
x
=
(
a
y
c
y
+
a
z
c
z
)
b
x
+
a
x
b
x
c
x
−
(
a
y
b
y
+
a
z
b
z
)
c
x
−
a
x
b
x
c
x
=
(
a
x
c
x
+
a
y
c
y
+
a
z
c
z
)
b
x
−
(
a
x
b
x
+
a
y
b
y
+
a
z
b
z
)
c
x
=
(
a
⋅
c
)
b
x
−
(
a
⋅
b
)
c
x
{\displaystyle {\begin{aligned}\{{\boldsymbol {a}}\times ({\boldsymbol {b}}\times {\boldsymbol {c}})\}_{x}&=a_{y}({\boldsymbol {b}}\times {\boldsymbol {c}})_{z}-a_{z}({\boldsymbol {b}}\times {\boldsymbol {c}})_{y}\\&=a_{y}(b_{x}c_{y}-b_{y}c_{x})-a_{z}(b_{z}c_{x}-b_{x}c_{z})\\&=a_{y}b_{x}c_{y}-a_{y}b_{y}c_{x}-a_{z}b_{z}c_{x}+a_{z}b_{x}c_{z}\\&=(a_{y}c_{y}+a_{z}c_{z})b_{x}-(a_{y}b_{y}+a_{z}b_{z})c_{x}\\&=(a_{y}c_{y}+a_{z}c_{z})b_{x}+a_{x}b_{x}c_{x}-(a_{y}b_{y}+a_{z}b_{z})c_{x}-a_{x}b_{x}c_{x}\\&=(a_{x}c_{x}+a_{y}c_{y}+a_{z}c_{z})b_{x}-(a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z})c_{x}\\&=({\boldsymbol {a}}\cdot {\boldsymbol {c}})b_{x}-({\boldsymbol {a}}\cdot {\boldsymbol {b}})c_{x}\end{aligned}}}
同様にして、y 成分、z 成分は、
{
a
×
(
b
×
c
)
}
y
=
(
a
⋅
c
)
b
y
−
(
a
⋅
b
)
c
y
{
a
×
(
b
×
c
)
}
z
=
(
a
⋅
c
)
b
z
−
(
a
⋅
b
)
c
z
{\displaystyle {\begin{aligned}&\{{\boldsymbol {a}}\times ({\boldsymbol {b}}\times {\boldsymbol {c}})\}_{y}=({\boldsymbol {a}}\cdot {\boldsymbol {c}})b_{y}-({\boldsymbol {a}}\cdot {\boldsymbol {b}})c_{y}\\&\{{\boldsymbol {a}}\times ({\boldsymbol {b}}\times {\boldsymbol {c}})\}_{z}=({\boldsymbol {a}}\cdot {\boldsymbol {c}})b_{z}-({\boldsymbol {a}}\cdot {\boldsymbol {b}})c_{z}\end{aligned}}}
ゆえに、
a
×
(
b
×
c
)
=
(
a
⋅
c
)
b
−
(
a
⋅
b
)
c
{\displaystyle {\boldsymbol {a}}\times ({\boldsymbol {b}}\times {\boldsymbol {c}})=({\boldsymbol {a}}\cdot {\boldsymbol {c}}){\boldsymbol {b}}-({\boldsymbol {a}}\cdot {\boldsymbol {b}}){\boldsymbol {c}}}
多次元への拡張 [ 編集 ] 行列式を使った拡張 [ 編集 ] 行列式による定義を拡張して、n 次元ベクトル空間における n - 1 項演算としてのベクトル積が
(
v
,
[
a
1
,
…
,
a
n
−
1
]
)
=
det
⟨
v
,
a
1
,
…
,
a
n
−
1
⟩
{\displaystyle ({\boldsymbol {v}},[{\boldsymbol {a}}_{1},\ldots ,{\boldsymbol {a}}_{n-1}])=\det \langle {\boldsymbol {v}},{\boldsymbol {a}}_{1},\ldots ,{\boldsymbol {a}}_{n-1}\rangle }
を定義できる。
完全反対称行列を用いれば
[
a
1
,
…
,
a
n
−
1
]
i
=
∑
j
1
,
…
,
j
n
−
1
ϵ
i
,
j
1
,
…
,
j
n
−
1
a
1
j
1
⋯
a
n
−
1
j
n
−
1
{\displaystyle [{\boldsymbol {a}}_{1},\ldots ,{\boldsymbol {a}}_{n-1}]_{i}=\sum _{j_{1},\ldots ,j_{n-1}}\epsilon _{i,j_{1},\ldots ,j_{n-1}}a_{1}^{j_{1}}\cdots a_{n-1}^{j_{n-1}}}
となる。
例えば、2次元のベクトル空間では単項演算 として
[
a
]
=
(
a
2
−
a
1
)
{\displaystyle [{\boldsymbol {a}}]={\begin{pmatrix}a_{2}\\-a_{1}\\\end{pmatrix}}}
となり、4次元ではそれぞれ三項演算 として
[
a
,
b
,
c
]
=
(
+
a
2
b
3
c
4
+
a
3
b
4
c
2
+
a
4
b
2
c
3
−
a
2
b
4
c
3
−
a
3
b
2
c
4
−
a
4
b
3
c
2
−
a
3
b
4
c
1
−
a
4
b
1
c
3
−
a
1
b
3
c
4
+
a
3
b
1
c
4
+
a
4
b
3
c
1
+
a
1
b
4
c
3
+
a
4
b
1
c
2
+
a
1
b
2
c
4
+
a
2
b
4
c
1
−
a
4
b
2
c
1
−
a
1
b
4
c
2
−
a
2
b
1
c
4
−
a
1
b
2
c
3
−
a
2
b
3
c
1
−
a
3
b
1
c
2
+
a
1
b
3
c
2
+
a
2
b
1
c
3
+
a
3
b
2
c
1
)
{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}},{\boldsymbol {c}}]={\begin{pmatrix}+a_{2}b_{3}c_{4}+a_{3}b_{4}c_{2}+a_{4}b_{2}c_{3}-a_{2}b_{4}c_{3}-a_{3}b_{2}c_{4}-a_{4}b_{3}c_{2}\\-a_{3}b_{4}c_{1}-a_{4}b_{1}c_{3}-a_{1}b_{3}c_{4}+a_{3}b_{1}c_{4}+a_{4}b_{3}c_{1}+a_{1}b_{4}c_{3}\\+a_{4}b_{1}c_{2}+a_{1}b_{2}c_{4}+a_{2}b_{4}c_{1}-a_{4}b_{2}c_{1}-a_{1}b_{4}c_{2}-a_{2}b_{1}c_{4}\\-a_{1}b_{2}c_{3}-a_{2}b_{3}c_{1}-a_{3}b_{1}c_{2}+a_{1}b_{3}c_{2}+a_{2}b_{1}c_{3}+a_{3}b_{2}c_{1}\\\end{pmatrix}}}
となる。また、1次元では定数 1 となる。
多元数を使った拡張 [ 編集 ] 3次元のクロス積
(
a
1
,
a
2
,
a
3
)
×
(
b
1
,
b
2
,
b
3
)
=
(
a
2
b
3
−
a
3
b
2
,
a
3
b
1
−
a
1
b
3
,
a
1
b
2
−
a
2
b
1
)
{\displaystyle (a_{1},a_{2},a_{3})\times (b_{1},b_{2},b_{3})=(a_{2}b_{3}-a_{3}b_{2},a_{3}b_{1}-a_{1}b_{3},a_{1}b_{2}-a_{2}b_{1})}
は、4元数 (
a
+
b
i
+
c
j
+
d
k
{\displaystyle a+bi+cj+dk}
b
i
+
c
j
+
d
k
{\displaystyle bi+cj+dk}
乗算
(
a
1
i
+
a
2
j
+
a
3
k
)
(
b
1
i
+
b
2
j
+
b
3
k
)
=
−
(
a
1
b
1
+
a
2
b
2
+
a
3
b
3
)
+
(
a
2
b
3
−
a
3
b
2
)
i
+
(
a
3
b
1
−
a
1
b
3
)
j
+
(
a
1
b
2
−
a
2
b
1
)
k
{\displaystyle (a_{1}i+a_{2}j+a_{3}k)(b_{1}i+b_{2}j+b_{3}k)=-(a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3})+(a_{2}b_{3}-a_{3}b_{2})i+(a_{3}b_{1}-a_{1}b_{3})j+(a_{1}b_{2}-a_{2}b_{1})k\,}
のベクトル成分で定義できる。ちなみに、スカラー成分を符号反転した
a
1
b
1
+
a
2
b
2
+
a
3
b
3
{\displaystyle a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}
内積 になっている。
3次元のクロス積はハミルトン の4元数 の概念をもとにして、ウィラード・ギブズ とオリヴァー・ヘヴィサイド がそれぞれ独立に、ドット積 と対になる数学的概念として考案した。
これを多元数に拡張すると、n + 1 元数の乗算から n 次元でのクロス積を定義できる。つまり、実数 (1元数)、複素数 (2元数)、4元数、8元数 の乗算から、0次元、1次元、3次元、7次元でのクロス積が定義できる(要素数が多くなるため縦ベクトルで表す)。
(
)
×
(
)
=
(
)
(
a
1
)
×
(
b
1
)
=
(
0
)
(
a
1
a
2
a
3
)
×
(
b
1
b
2
b
3
)
=
(
a
2
b
3
−
a
3
b
2
a
3
b
1
−
a
1
b
3
a
1
b
2
−
a
2
b
1
)
(
a
1
a
2
a
3
a
4
a
5
a
6
a
7
)
×
(
b
1
b
2
b
3
b
4
b
5
b
6
b
7
)
=
(
a
2
b
3
−
a
3
b
2
−
a
4
b
5
+
a
5
b
4
−
a
6
b
7
+
a
7
b
6
−
a
1
b
3
+
a
3
b
1
−
a
4
b
6
+
a
5
b
7
+
a
6
b
4
−
a
7
b
5
a
1
b
2
−
a
2
b
1
−
a
4
b
7
−
a
5
b
6
+
a
6
b
5
+
a
7
b
4
a
1
b
5
+
a
2
b
6
+
a
3
b
7
−
a
5
b
1
−
a
6
b
2
−
a
7
b
3
−
a
1
b
4
−
a
2
b
7
+
a
3
b
6
+
a
4
b
1
−
a
6
b
3
+
a
7
b
2
a
1
b
7
−
a
2
b
4
−
a
3
b
5
+
a
4
b
2
+
a
5
b
3
−
a
7
b
1
−
a
1
b
6
+
a
2
b
5
−
a
3
b
4
+
a
4
b
3
−
a
5
b
2
+
a
6
b
1
)
{\displaystyle {\begin{aligned}&()\times ()=()\\&(a_{1})\times (b_{1})=(0)\\&{\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}\times {\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}={\begin{pmatrix}a_{2}b_{3}-a_{3}b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2}-a_{2}b_{1}\end{pmatrix}}\\&{\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\\a_{4}\\a_{5}\\a_{6}\\a_{7}\end{pmatrix}}\times {\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\\b_{4}\\b_{5}\\b_{6}\\b_{7}\end{pmatrix}}={\begin{pmatrix}a_{2}b_{3}-a_{3}b_{2}-a_{4}b_{5}+a_{5}b_{4}-a_{6}b_{7}+a_{7}b_{6}\\-a_{1}b_{3}+a_{3}b_{1}-a_{4}b_{6}+a_{5}b_{7}+a_{6}b_{4}-a_{7}b_{5}\\a_{1}b_{2}-a_{2}b_{1}-a_{4}b_{7}-a_{5}b_{6}+a_{6}b_{5}+a_{7}b_{4}\\a_{1}b_{5}+a_{2}b_{6}+a_{3}b_{7}-a_{5}b_{1}-a_{6}b_{2}-a_{7}b_{3}\\-a_{1}b_{4}-a_{2}b_{7}+a_{3}b_{6}+a_{4}b_{1}-a_{6}b_{3}+a_{7}b_{2}\\a_{1}b_{7}-a_{2}b_{4}-a_{3}b_{5}+a_{4}b_{2}+a_{5}b_{3}-a_{7}b_{1}\\-a_{1}b_{6}+a_{2}b_{5}-a_{3}b_{4}+a_{4}b_{3}-a_{5}b_{2}+a_{6}b_{1}\end{pmatrix}}\end{aligned}}}
これら以外の次元では、必要な対称性 を持つ乗算が定義できないため(これはアドルフ・フルヴィッツ によって証明された)、クロス積は定義できない。また、0次元では自明なことを確認できるにすぎず、1次元のクロス積は常に零ベクトル である。
直積を使った拡張(外積) [ 編集 ] クロス積は、直積
a
∘
b
=
a
b
⊺
=
(
a
i
b
j
)
{\displaystyle {\boldsymbol {a}}\circ {\boldsymbol {b}}={\boldsymbol {a}}{\boldsymbol {b}}^{\intercal }=(a_{i}b_{j})}
を使って
a
×
b
=
a
∘
b
−
b
∘
a
{\displaystyle {\boldsymbol {a}}\times {\boldsymbol {b}}={\boldsymbol {a}}\circ {\boldsymbol {b}}-{\boldsymbol {b}}\circ {\boldsymbol {a}}\quad }
と定義できる。ただしここで、反対称テンソル と擬ベクトル を等価
(
x
,
y
,
z
)
=
(
0
z
−
y
−
z
0
x
y
−
x
0
)
{\displaystyle (x,y,z)={\begin{pmatrix}0&z&-y\\-z&0&x\\y&-x&0\end{pmatrix}}}
としたが、これをホッジ作用素
⋆
{\displaystyle \star }
写像 として明示すると
a
×
b
=
⋆
(
a
∘
b
−
b
∘
a
)
{\displaystyle {\boldsymbol {a}}\times {\boldsymbol {b}}=\star ({\boldsymbol {a}}\circ {\boldsymbol {b}}-{\boldsymbol {b}}\circ {\boldsymbol {a}})}
と書ける。
(*)式はそのまま、一般次元での定義に使える。ただし、これで定義できる積は、クロス積ではなく外積 と呼び、
a
∧
b
=
a
∘
b
−
b
∘
a
{\displaystyle {\boldsymbol {a}}\wedge {\boldsymbol {b}}={\boldsymbol {a}}\circ {\boldsymbol {b}}-{\boldsymbol {b}}\circ {\boldsymbol {a}}}
で表す。外積は3次元ではクロス積に一致するが、同義語ではないので注意が必要である。
外積は2階の反対称テンソルであり、これはホッジ作用素により、n 次元では n - 2 階の擬テンソル に写像できる。つまり、2次元では擬スカラー (0階の擬テンソル)、3次元では擬ベクトル (1階の擬テンソル)に写像できるが、4次元以上ではテンソルとして扱うしかない。
外積(ドイツ語 : äußeres Produkt )は、グラスマン によって導入されたが、当時はそれほど注目されず、彼の死後に高く評価された。
関連項目 [ 編集 ] 外部リンク [ 編集 ] 





![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9312534b1ba4c99e32566a32c071977ddad384b)







![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]_{1}=({\boldsymbol {e}}_{1},[{\boldsymbol {a}},{\boldsymbol {b}}])={\begin{vmatrix}1&a_{1}&b_{1}\\0&a_{2}&b_{2}\\0&a_{3}&b_{3}\\\end{vmatrix}}=a_{2}b_{3}-a_{3}b_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4349b2fce366207e757ca54392f753a52fc9da0d)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]_{2}=({\boldsymbol {e}}_{2},[{\boldsymbol {a}},{\boldsymbol {b}}])={\begin{vmatrix}0&a_{1}&b_{1}\\1&a_{2}&b_{2}\\0&a_{3}&b_{3}\\\end{vmatrix}}=a_{3}b_{1}-a_{1}b_{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1511f42e28b2c8732131ea0bb027b684aa993e2)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]_{3}=({\boldsymbol {e}}_{3},[{\boldsymbol {a}},{\boldsymbol {b}}])={\begin{vmatrix}0&a_{1}&b_{1}\\0&a_{2}&b_{2}\\1&a_{3}&b_{3}\\\end{vmatrix}}=a_{1}b_{2}-a_{2}b_{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9f0207a5c8f10efb689e85cd510d213bb15f162)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]\doteq {\begin{pmatrix}a_{2}b_{3}-a_{3}b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2}-a_{2}b_{1}\\\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52d2a2643983ecdda9538f4b90fb3cc53f0423f4)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]={\begin{vmatrix}{\boldsymbol {e}}_{1}&a_{1}&b_{1}\\{\boldsymbol {e}}_{2}&a_{2}&b_{2}\\{\boldsymbol {e}}_{3}&a_{3}&b_{3}\end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ecdc5222d6868cc91016a795adf8011d2b9f5bf)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]_{i}=\sum _{j,k}\epsilon _{ijk}a_{j}b_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2e2b0ca64f606d305621506a8566769c3b6f6a6)



![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {a}}]={\boldsymbol {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de09f61713ceb571793a08c86640e65fca795744)


![{\displaystyle [{\boldsymbol {a}},k{\boldsymbol {b}}+l{\boldsymbol {c}}]=k[{\boldsymbol {a}},{\boldsymbol {b}}]+l[{\boldsymbol {a}},{\boldsymbol {c}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1a89fae470f1fdcdca0259bb3136f179e7982f0)
![{\displaystyle [k{\boldsymbol {b}}+l{\boldsymbol {c}},{\boldsymbol {a}}]=k[{\boldsymbol {b}},{\boldsymbol {a}}]+l[{\boldsymbol {c}},{\boldsymbol {a}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9c73e1f490b1534bc0d5a0dd98af0735a19ced7)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {0}}]=[{\boldsymbol {0}},{\boldsymbol {a}}]={\boldsymbol {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90fd83f7cab062ccbe03547df7ef0dbc69b29d75)
![{\displaystyle [{\boldsymbol {a}},[{\boldsymbol {b}},{\boldsymbol {c}}]]=({\boldsymbol {a}},{\boldsymbol {c}})\,{\boldsymbol {b}}-({\boldsymbol {a}},{\boldsymbol {b}})\,{\boldsymbol {c}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac7503be70399904420db5aeeba3d86b227bd75c)
![{\displaystyle [{\boldsymbol {a}},[{\boldsymbol {b}},{\boldsymbol {c}}]]-[[{\boldsymbol {a}},{\boldsymbol {b}}],{\boldsymbol {c}}]\neq {\boldsymbol {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe4ad1428e449a33b245c7890946b37a4bea4ca4)
![{\displaystyle [{\boldsymbol {a}},[{\boldsymbol {b}},{\boldsymbol {c}}]]-[[{\boldsymbol {a}},{\boldsymbol {b}}],{\boldsymbol {c}}]=[{\boldsymbol {b}},[{\boldsymbol {a}},{\boldsymbol {c}}]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e2a27c9dfd413efb3160594702c7b452389b76d)
![{\displaystyle [{\boldsymbol {a}},[{\boldsymbol {b}},{\boldsymbol {c}}]]+[{\boldsymbol {b}},[{\boldsymbol {c}},{\boldsymbol {a}}]]+[{\boldsymbol {c}},[{\boldsymbol {a}},{\boldsymbol {b}}]]={\boldsymbol {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56d607faf2e8a034576fcf65d9632c1dc5c1853e)






![{\displaystyle ({\boldsymbol {v}},[{\boldsymbol {a}}_{1},\ldots ,{\boldsymbol {a}}_{n-1}])=\det \langle {\boldsymbol {v}},{\boldsymbol {a}}_{1},\ldots ,{\boldsymbol {a}}_{n-1}\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c7f2ed5805dda8d32ec655e9e7c00f0591e4be8)
![{\displaystyle [{\boldsymbol {a}}_{1},\ldots ,{\boldsymbol {a}}_{n-1}]_{i}=\sum _{j_{1},\ldots ,j_{n-1}}\epsilon _{i,j_{1},\ldots ,j_{n-1}}a_{1}^{j_{1}}\cdots a_{n-1}^{j_{n-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1849fb2030deceaab3a16064c64f671236ab5ec6)
![{\displaystyle [{\boldsymbol {a}}]={\begin{pmatrix}a_{2}\\-a_{1}\\\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffd2fada44669d3c8511498290b506659f8e4891)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}},{\boldsymbol {c}}]={\begin{pmatrix}+a_{2}b_{3}c_{4}+a_{3}b_{4}c_{2}+a_{4}b_{2}c_{3}-a_{2}b_{4}c_{3}-a_{3}b_{2}c_{4}-a_{4}b_{3}c_{2}\\-a_{3}b_{4}c_{1}-a_{4}b_{1}c_{3}-a_{1}b_{3}c_{4}+a_{3}b_{1}c_{4}+a_{4}b_{3}c_{1}+a_{1}b_{4}c_{3}\\+a_{4}b_{1}c_{2}+a_{1}b_{2}c_{4}+a_{2}b_{4}c_{1}-a_{4}b_{2}c_{1}-a_{1}b_{4}c_{2}-a_{2}b_{1}c_{4}\\-a_{1}b_{2}c_{3}-a_{2}b_{3}c_{1}-a_{3}b_{1}c_{2}+a_{1}b_{3}c_{2}+a_{2}b_{1}c_{3}+a_{3}b_{2}c_{1}\\\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e21e567381f509202aa3e7ffd6841c1297e8f9e0)











