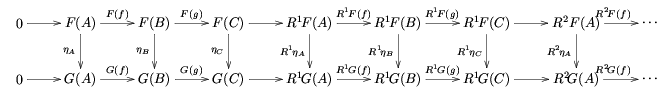導来関手
数学では、一部の関手から導来 (どうらい、英語: derived) することにより、元の関手と密接に関連した新しい関手を得ることができる。導来という操作は、抽象的ではあるが、数学全体を通して多くの構成を統一する。
動機[編集]
さまざまな状況で短完全系列が長完全系列に持ち上がることが分かっている。導来関手の概念はこれらの結果の多くを明確に根拠づけることができる。
2つのアーベル圏 A と B の間の共変な左完全関手 F : A → B が与えられ、0 → A → B → C → 0 を A の短完全系列とすると、F を適用することで完全系列 0 → F(A) → F(B) → F(C) が得られる。この系列をどのように右へ拡張し長完全系列とするかが問題になるが、与えられた短完全系列を右へ拡張する方法には多数の異なる方法があるので、厳密には、この問は適切とは言えない。しかし、A が充分に「良い」性質を持っている場合は、F の右導来関手による標準形がひとつ存在する。全ての i ≥ 1 に対して、関手 RiF: A → B が存在して、上記の短完全系列は次のように右へと拡張される。
このことから、F が完全関手であることと、R1F = 0 であることとは同値であるので、F の右導来関手は F がその程度完全から乖離しているかの目安であることが分かる。
短完全系列の中の対象 A が単射対象 (injective object) であれば、系列は分裂する(分裂補題)。任意の加法関手を分裂する系列へ適用すると、結果も分裂系列になり、特に、R1F(A) = 0 である。右導来関手は単射対象では 0 である。このことが以下の構成の動機である。
構成と最初の性質[編集]
アーベル圏 A を考える上での重要な仮定は、圏 A が充分単射的であることである。この充分単射的とは、A の全ての対象 A に対し、A の単射対象 (injective object) であるような I が存在して、モノ射 A → I が存在することである。
共変的な左完全関手 F : A → B の右導来関手は、次の様に定義される。A の対象 X より始めると、充分な単射対象を使って、次の形の長完全系列を構成することができる。
ここに I i は全て単射的な対象である(これは X の単射分解として知られている)。関手 F をこの完全系列へ適用し、第一項を落とすと、鎖複体
を得る。
注意:一般にはこれはもはや完全系列ではない。しかし、i 次のホモロジー (F(Ii) からの射の核を、F(Ii) への射の像で割ったもの)を計算することができる。この結果を RiF(X) と呼ぶ。もちろん、多くのことを検証する必要がある。つまり、最終的な結果は与えられた X の単射分解に依存せず、射 X → Y は自然に射 RiF(X) → RiF(Y) を誘導するので、実際に関手となっている。左完全性は、
が完全であることを意味するので、 であり、 に対しのみ、興味深い何かを得ることができる。
(テクニカルには、F の well-defined な導出のためには、Aの全対象に対し単射分解を固定する必要がある。この単射分解の選択は、関手 RiF をもたらす。異なった分解を選択しても、自然に同型な関手となり、結局、選択は問題でない。)
上に述べた短完全系列から長完全系列へ変換する性質は、蛇の補題の結果である。このことは、導来関手の集まりはδ-関手 (Delta-functor) であることを教えてくれる。
X 自身を単射的とすると、単射分解 0 → X → X → 0 を選ぶことができ、全ての i ≥ 1 に対し、RiF(X) = 0 を得る。実用では、この事実は、長完全系列の性質と組合わせて、右導来関手の値の計算に良く使われる。
RiF(X) の計算には同値な別の方法もある。X の単射分解を上記のように取り、Ki を射 Ii-1 → Ii の像とする(i = 0 に対し、Ii-1 = 0 と定義する)と、これは Ii → Ii+1 の核と同じになる。φi : Ii-1 → Ki を対応するエピ射とすると、RiF(X) は F(φi) の余核となる。
変形[編集]
共変な右完全関手 G と圏 A が充分に射影的(つまり、A の対象 A に対し、射影的対象 P とエピ射 P → A が存在する)とすると、右導来関手と同様に左導来関手 LiG を定義することができる。A の対象 X に対し、まず、次の形の射影的分解を構成する。
ここに、各 Pi は射影的対象である。G をこの系列に適用し、最後の項を落としホモロジーを計算し、LiG(X) を得る。前と同様に、L0G(X) = G(X) となる。
この場合には、長完全系列は右ではなくて左側へ拡張され、
が、
となる。
左導来関手は全ての射影的対象上で 0 である。
また、反変 (contravariant) 左完全関手 F から始めることもでき、このとき右導来関手はまた反変である。短完全系列
から長完全系列
が得られる。
これらの右導来関手は射影的対象上では 0 であるので、射影的分解を通して計算される。
応用[編集]
層コホモロジー: X を位相空間とすると、X 上の全てのアーベル群の層の圏は、充分な単射的対象を持つアーベル圏である。そのような層 L に大域切断の群 L(X) を対応させる関手は左完全であり、右導来関手は層コホモロジー関手であり、通常、H i(X, L) と書かれる。少し一般化し、(X, OX) を環付き空間とすると、OX-加群の全ての層の圏は充分単射的な加群を持つアーベル圏であり、再度、大域切断関手の右導来関手として層コホモロジーを構成することができる。
エタール・コホモロジーは、スキーム上のコホモロジー論である。これはエタール景上のアーベル群の層の大域切断関手の右導来関手である。
Ext関手: R が環であれば、全ての左 R-加群の圏は、充分に単射的な対象をもったアーベル圏である。左 R-加群 A を固定すれば、Hom関手 Hom(A, -) は左完全で、その右導来関手はExt関手 ExtRi(A, -) である。
Tor関手: 左 R-加群の圏も充分な射影的対象を持っている。A が固定された右 R-加群であれば、A とのテンソル積は左 R-加群上の右完全な共変関手を与え、その左導来関手はTor関手 TorR
i (A, -) を与える。
群コホモロジー (Group cohomology): G を群とすると、G-加群 M は、自己同型群として G が作用するアーベル群 M である。この M は群環 ZG 上の加群と同一である。G-加群は、充分な単射対象を持つアーベル圏を形成する。G が固定する M の元の全てから構成される M の部分群を MG と書く。これは左完全関手であり、この右導来関手は群コホモロジー関手でもあり、一般的には、H i(G, M) と書かれる。
自然性[編集]
導来関手と長完全系列は、いくつかのテクニカルな意味で「自然」である。
第一に、
(この図の行は完全)の形の可換図式が与えられると、結果として得られる長完全系列は、次の可換図式により関係付けられる。
第二に、η: F → G を左完全関手 F から左完全関手 G への自然変換とすると、自然変換 Riη: RiF → RiG が引き起こされ、実際、引き起こされた Ri は A から B へのすべての左完全関手からなる関手圏 (functor category) から、A から B へのすべての関手の関手圏への関手となる。さらに、この関手は、次の意味で長完全系列と整合性をもっている。
が短完全系列であれば、可換図形
が引き起こされる。
これらの自然性は両方とも、蛇の補題によりもたらされる系列の自然性から来る。
逆に、次の導来関手の特徴づけが成り立つ。A のすべての単射的対象 I とすべての正の整数 i に対して Ri (I) = 0 が成り立つような、上記を満たす関手の族 Ri: A → B、つまり、短完全系列を長完全系列へ写すものが与えられると、それらの関手は R0 の右導来関手である。
一般化[編集]
より現代的な(より一般的な)導来関手のアプローチは導来圏のことばで扱われる。
文献[編集]
- Manin, Yuri Ivanovich; Gelfand, Sergei I. (2003), Methods of Homological Algebra, Berlin, New York: Springer-Verlag, ISBN 978-3-540-43583-9
- Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, 38, Cambridge University Press, ISBN 978-0-521-55987-4, OCLC 36131259, MR1269324