テブナンの定理

テブナンの定理（テブナンのていり、英: Thevenin's theorem）は電気回路に関する定理で、複数の直流電源を含む電気回路に負荷を接続したときに得られる電圧や負荷に流れる電流を、単一の内部抵抗のある電圧源に変換して求める方法である。

概要

電圧源、電流源、抵抗のみを含むどんなブラックボックスでもテブナン等価回路に変えることができる

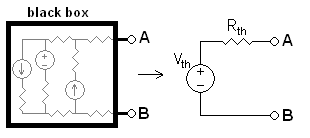
右の図で、回路網の出力端子A–B間の開放電圧を V_th, 端子A–B間から見た回路網の内部抵抗を R_th, A–B間に接続する負荷の抵抗値を R_L, 負荷に流れる電流を I_L, 負荷を接続したときの端子A–B間の電圧を V_L とすると、次の関係が成立する。

${\begin{aligned}I_{L}&={\frac {1}{R_{\text{th}}+R_{L}}}V_{\text{th}}\\V_{L}&={\frac {R_{L}}{R_{\text{th}}+R_{L}}}V_{\text{th}}\end{aligned}}$

なお、回路網の内部抵抗を求める場合、電圧源は短絡、電流源は開放して考えればよい。ただし、電圧・電流源に内部抵抗が存在する場合は当然、考慮しなければならない。

名称について

1883年にフランス郵政・電信省の技術者、レオン・シャルル・テブナンにより発表され、「テブナンの定理」と呼ばれていたが、それより前の1853年にドイツの物理学者、ヘルマン・フォン・ヘルムホルツにより発表されていたことが、1950年にドイツの物理学者ハンス・フェルディナント・マイヤー (Hans Ferdinand Mayer) により英文で指摘されたため、ヘルムホルツ-テブナンの定理 (Helmholtz–Thevenin's theorem) とも呼ばれる。また、ヘルムホルツが最初の発表者であることを尊重する立場から、数学（ベクトル解析）におけるヘルムホルツの定理と区別して、「ヘルムホルツ等価回路」と呼ばれることもある。

日本では等価電圧源表示（とうかでんあつげんひょうじ）、また交流電源の場合に成立することを1919年（1922年、1923年）に発表した鳳秀太郎の名を取って、鳳–テブナンの定理（ほう–テブナンのていり）ともいう。この別称に関して、東京工業大学の教授だった川上正光は著書の中で早稲田大学の教授だった黒川兼三郎の発意によるものと記述しているが、これは思い違いであり、正しくは東北帝国大学の教授だった抜山平一と、助教授だった渡辺寧の両名の発意によるものとなる。

関連項目

• ノートンの定理 - テブナンの定理の双対。等価電流源表示。
• 重ね合わせの原理
• 電圧源 - 電流源
• 電気回路 - 直流回路 - 直列回路と並列回路
• 等価回路