適応度
適応度(てきおうど、英: fitness)は生物学、とくに集団遺伝学など数理生物学分野で用いられる語である。
古典的適応度[編集]
字義通りに理解すれば、その生物個体がどれほどその生活する環境に適応しているかを示す値である。しかし、これには出産数や出産間隔など直接的に繁殖に関わる特性だけでなく筋力や視力、体の大きさといった多くの特性も間接的に関わってくる。このことから、適応度はその個体が生物として繁栄していく能力を総体として捉えるための概念と捉えることができる。チャールズ・ダーウィンの時代に用いられた適応度 (Fitness) はこの意味であり、現在でも「適応的(生き延びるのに適した性質だろう)」と同様の意味として「適応度が高い」と用いることがある。
個体適応度と遺伝的適応度[編集]
現在一般に用いられている定義としては、一般的には自然選択説の考えに立ち、より多く子供を残すものが選択されるのだから、「ある生物個体がその生涯で生んだ次世代の子のうち、繁殖年齢まで成長できた子の数」となる。動物学などのフィールドワークや実験では遺伝的適応度を計測することは困難であるため、この定義を近似値として用いる。これを個体適応度と呼ぶ。また子の実数で表す適応度のことを絶対適応度と呼ぶ。個体数が安定した環境では、平均的な絶対適応度は1である。しかし繁殖戦略によっては、次世代の子供の数が同じでも孫の数に差が出ることもある(「フィッシャーの原理」も参照)。そのためより正確な(厳密ではないが)表現としては「十分遠い将来のある世代に残った子孫の数」と言うことができる。
一方、遺伝的適応度は「ある形質をもたらす対立遺伝子(進化ゲーム理論の場合は戦略)が集団中に広まる速度」と言うことができる。たとえば二組のペアがおり、一方が遺伝子Xの影響で生涯に6匹の子をもうけたとする。もう一方は対立遺伝子Yの影響によって生涯に4匹の子をもうけたとする。この群れの平均産子数は (4 + 6) / 2 = 5 であり、Xの適応度は 6 / 5 = 1.2 となる。Yの適応度は 4 / 5 = 0.8 となる。この値を相対適応度と呼ぶ。集団遺伝学、数理生態学などで通常用いられるのは遺伝的適応度であり、相対適応度である。遺伝的適応度は個体適応度と一致しない場合がある。集団全体の相対適応度は常に1であり、相対適応度が1であればその遺伝子は広まりも減りもしないが、1より小さければ集団内で次第に数を減らし、1より大きければ次第に数を増す。値が大きければ大きいほど急速に広まる。この例ではXが増してゆく。
適応度地形[編集]
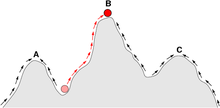

適応度地形(英語: fitness landscape)は1923年にシューアル・ライトらによって提唱された、遺伝子型と生殖成功率の関係(適応度)を視覚化するために用いられる数学的モデルである。例えば2次元空間上に個体群の各生物個体を配置したとすれば、そこに「高さ」の軸を追加してその軸の値に適応率を当てはめると起伏のある曲面が得られる。この曲面を適応度地形と呼ぶ。
適応度地形の概念を用いると、適応度の高い個体がその数を増やし低い個体は数を減らしていく様子を説明しやすい。適応度が高い個体は適応度地形の中で「高さ」が高い位置におり、適応度の低い個体は低い位置にいる。個体群はより多くの個体を高い位置に置こうとして低い位置の個体は次第に数を少なく、高い位置にいる個体の数を多くなるように繁殖を行う。図に示したときこれはあたかも曲面上の起伏を登っているかのように振る舞う。
包括適応度[編集]
適応度をある個体の子孫だけでなくその親族、あるいは同じ対立遺伝子を持つ可能性のある他個体にまで広げたものを包括適応度と言う。社会性行動の進化を扱うさいには包括適応度を用いなければならない。この場合は通常、子にも包括適応度における血縁度の計算が適用される(有性生殖では子の遺伝的価値は親の半分であり、親子の進化的対立の原因である)。包括適応度は遺伝的適応度の概念の一つであり、包括適応度を個体の数で計算すると混乱の原因となる。包括適応度の上昇はある社会行動の効果に対して用いられる。例えば自分が親族を助けたことでその親族が多くの子を残した場合、自分の「利他行動に関する対立遺伝子」の包括適応度が上昇する。全く別の地域に移住し相互作用できなくなった親族が子を産んでも自分の包括適応度が上昇したことにはならない。
適応度の概念を提唱し、数学的なモデルとして構築したのは集団遺伝学者ロナルド・フィッシャー、J・B・S・ホールデン、シューアル・ライトらであった。W.D.ハミルトンはこれを拡張して包括適応度を提唱した。さらに後年、G.プライスの共分散則を取り入れて、包括適応度を親族以外にも適用できる概念へと拡張した。
計算機科学への応用[編集]
自然選択説を計算に応用した遺伝的な最適化問題では、集団内の個体[脚注 1]のもつさまざまな特徴から適応度を算出し個々の個体が問題に適当かを判定する。この適応度を判定する関数を適応度関数と呼ぶ。算出された適応度が高い個体は多くの子孫[脚注 2]を残し、適応度が低い個体は子孫をあまり残さずに最終的に絶滅していくことで求める解に徐々に近づいていく。
適応度地形は最適化問題でも用いられ、山登り法、最急降下法、共役勾配法、焼きなまし法などの最適化アルゴリズムは、適応度地形上での最良の値(最大値または最小値)を探索すると考えられる。
適応度関数[編集]
適応度関数(てきおうどかんすう)またはフィットネス関数(英: Fitness function)は、一種の目的関数であり、遺伝的アルゴリズムにおける解[脚注 3]の最適度を定量化し、特定の遺伝子が他の遺伝子より優れていることを示す。最適な遺伝子、あるいは少なくとも他よりも比較的最適な遺伝子で、「交叉」などの遺伝的操作が行われ、よりよい(と期待される)次世代を生み出す。理想的な適応度関数は、アルゴリズムの目的に密接に関連し、素早く計算できる。遺伝的アルゴリズムは何度も何度も世代交代を繰り返す必要があり、実行速度は非常に重要である。
適応度関数の定義は直接的でないことが多く、GA(遺伝的アルゴリズム)によって生成される最適解が期待したものでない場合は繰り返し実行される。場合によっては、適応度関数をどう定義すべきかも明らかでないことがある。このため、遺伝的アルゴリズムでの解の評価を外部エージェント(通常、人間)に任せる場合もある。
参考文献[編集]
- Haldane, J.B.S. (1924) "A mathematical theory of natural and artificial selection" Part 1 Transactions of the Camrbidge philosophical society: 23: 19-41 link (pdf file)
- Hamilton, W.D. (1964) "The evolution of social behavior" Journal of Theoretical Biology 1:...
- リチャード・ドーキンス 著、日高敏隆ほか 訳『延長された表現型 : 自然淘汰の単位としての遺伝子』紀伊国屋書店、1987年(原著1982年)。ISBN 4-314-00485-1。 -「適応度狩り」の章で異なる五種の適応度について概説している。
脚注[編集]
関連項目[編集]
外部リンク[編集]
- Evolution A-Z: Fitness
- fitness (英語) - スタンフォード哲学百科事典「適応度」の項目。
